初中数学教学中如何引导学生高效学习

李参

摘 要 数学教学必须重视对学生学习数学的学法指导，授之与渔才能使教材、教法、学法形成一个协调的整体，从而全面提高数学教学质量。让学生知其然，也知其所以然，形成一定的学习能力，并从根本上掌握学习数学的方法。

关键词 数学教学;学法指导;培养能力;创新思维

中图分类号：G632 文献标识码：A 文章编号：1002-7661（2020）02-0092-03

随着新课程改革的不断推进，新教材要求学生自主思考，在亲身体验和探索中去理解和掌握知识、技能和方法。然而教师整合教材的能力滞后以及学生脆弱的思维品质强烈冲击着新教材的目标和要求，形成了教师只重视教法，学生学而无法的矛盾。授之与渔才能使教材、教法、学法形成一个协调的整体，因此，我在数学课堂教学中重视对学生学习数学的学法指导，从而全面提高数学教学质量。

一、指导学生阅读数学课本，培养自学能力

初中学生往往不会阅读数学课本，不善于预习，认为阅读课本就是看看结论，看不出问题和疑点，例如，“全等三角形的对应角相等”，他们背得滚瓜烂熟，但解题应用时见到角就相等，根本不理解“对应角”的概念。因此，指导学生阅读数学课本时应注重以下几点：

（一）粗读，先粗略地浏览课本有关章节的内容，掌握章节的概貌及重难点，对課本上难以理解的内容作出符号记录。例如，全等三角形的对应角、对应边是指哪些角、哪些边，最后带着疑问去听课。

（二）细读，对重要的概念、公式、法则、定理的反复阅读、体会、思考，注意知识的形成的条件和发展过程。如在阅读锐角三角函数时，指导学生找出概念形成所需的条件，可以从“直角三角形30o所对的直角边等于斜边的一半”推导出锐角的对边（邻边）与斜边的比是一个固定值，然后得出直角三角形任何一个锐角的对边（邻边）与斜边的比都是一个固定值。最后形成正弦、余弦的概念，体现了从特殊到一般的数学思想。

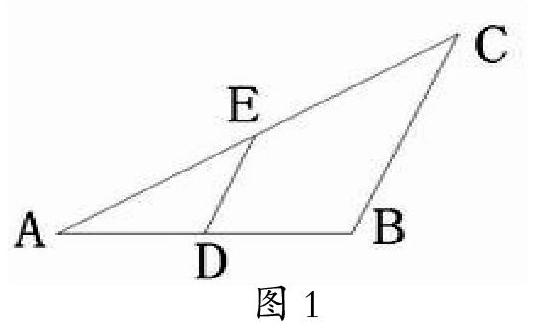
（三）精读，弄清知识的内在联系，重视文字、符号及图形之间的互译。例如，平行、垂直、等名词，它们的符号语言是什么？图形语言是什么？对于定理与图形之间的互译就更加重要，例如，对中位线定理的互译，如图1，已知D、E分别是⊿ABC的AB、AC上的中点。

结论：DE∥BC，DE=BC。在解题书写中译为：图1

∵D、E分别是⊿ABC的AB、AC上的中点，

∴DE是⊿ABC的中位线，

∴DE∥BC，DE=BC。

这样可以使学生深入理解定理，也可以让学生学会从已知获得解题所需的条件，还可以让学生学会几何证明的书写，培养学生完整的思维力。

这三个步骤分别安排在不同的学习时期完成，粗读安排在预习时完成，细读在教师讲授的当晚完成，精读在章节复习时进行。这样可以对知识进行分类、归纳、总结，研讨课本对知识安排的意图，完善认知结构，把课本读“薄”。

二、指导学生听课，培养学生的创新思维能力

在教学中指导学生听课，先从培养学习兴趣入手以集中学生的注意力，使其激活原有的认知结构专心听课，其次指导学生听课时注意听好课堂知识的具体细节，①听每节课的学习目标要求;②听新知识的引入和形成过程;③听教师对重点、难点知识的剖析;④尤其是听教师在知识点应用时关键部分的提示和处理，以及例题的解题思路和解题方法的渗透更为重要。笔者坚持“以教师为主导，以学生为主体，以训练为主线”的教学模式，根据每个课堂知识的要求和学生的实际情况，设计可以启发学生思维的问题，让学生获得启发并领悟知识。我在数学课堂教学中常用下面两种做法去培养学生。

（一）引导学生学会质疑，培养学生的创新思维

清朝学者陈宪章说过“学贵有疑，小疑则小进，大疑则大进”。笔者鼓励学生在阅读和解题中发现问题、提出问题、讨论问题、解决问题，这是学生理解知识的过程，也是激发学生的创新意识的过程。

如在学习《因式分解法解一元二次方程》一节时，在学习了因式分解法后，笔者再让学生用直接开平方法解方程X2=9，因式分解法X2-9=0，鼓励学生对比两个方程的解法，提出质疑，X2=9可用因式分解法吗？让学生不能满足于一般的感受和现成的结论，要多问几个“为什么”，要敢于“独辟蹊径”，激发学生的创新思维。

（二）精心设计问题，培养学生的创新思维

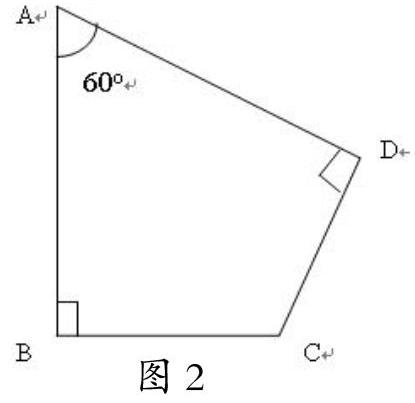
问题是思维的核心，只有合乎引导实际性问题，才能激发学生积极思考和探索。案例1：在学习《解直角三角形的应用》一节时，笔者设计了这样一道练习题：如图2，在四边形ABCD中，AB=2，CD=1，∠A=60o，∠B=∠D=90o，求四边形ABCD的面积，在解这道练习题前我设计了以下三个问题：

（1）应用解直角三角形解决四边形有哪些辅助线转化为解直角三角形的问题？

（2）你构造的直角三角形满足解直角三角形的条件吗？

（3）你有多少种构造方法？

在这三个问题的引导下，学生进入了深思，并在同学们中激起了激烈的讨论。同学们讨论后得出了如图甲、乙、丙三种构造直角三角形进行解题的方法。

丁所示的构图破坏了60o角的条件，不能满足解直角三角形的条件。通过这样设计问题，使学生在理解知识和激发学生的创新思维两个方面发挥得淋漓尽致，收到了很好的教学效果。

案例2：在学习了《图形的旋转》后笔者设计了这样一道练习题：

如图3，在直角梯形ABCD中，AD∥BC，AB⊥BC，AD=3，BC=5，将CD以D为旋转中心逆时针旋转90o至DE，连结AE，试求⊿ADE的面积。在解这道练习题前我用以下三个问题引导学生思考分析：

（1）计算三角形的面积要满足什么条件？题 图3

目前题中已有什么条件？欠什么条件？

（2）看CD以D为旋转中心逆时针旋转90o至DE，结合图形的旋转你可以想到什么？

（3）请将你想到的图形的旋转，动手将旋转后的图形画出来，看看是否能找到解题的突破口。

学生在这三个问题的引导下，得到了如甲图将直角梯形ABCD以D为旋转中心逆时针旋转90o，如图乙将⊿ADE以D为旋转中心顺时针旋转90o的两种解题方案，很快找出了计算⊿ADE的面积的另一个条件，并解出正确结果。

我这样设计，能使学生分析问题易于入手，并能增强学生的信心和激发探究欲望，打破学生的惯性思维，深入地挖掘和探讨解题的方法，同时领悟知识，达到即整合知识，又可以成功地培养学生的创新思维。

三、指导学生课后先复习巩固后解题，培养归纳、类比能力

很多学生课后往往急于完成书面作业而忽视必要的反思，以致出现照例题模仿套公式解题，为交作业而作业或抄袭作业。因此，在这个环节的学法指导上，我要求学生做到如下几点要求。

（一）反思教师在课堂上的解题思路，回忆同学之间的不同解法，领悟知识的来龙去脉，反思如何实施文字语言、符号语言、图形语言之间的相互转换。

（二）解题是学习数学的核心，教会学生学会思考，解题灵活变通。指导学生解题时要求学生注意解题的分析过程而不是抄袭答案，善于读懂数学题目的“哑语”，挖掘隐含条件，思考破解题目的关键，并根据题目条件迅速构建数学“图形”或“模型”确立等量关系或数量关系，这样就能领悟较多的知识。

（三）当一个单元知识学习之后指导学生将该单元知识、内容再全面地看一遍，指导学生掌握认知结构和各知识点的关联，打破课与课的界限，将分散在各章的知识连成线、结成网。例如，在学习了用坐标表示位似图形变换后，指导学生联想如何用坐标表示平移、轴对称、中心对称的变换，比较各种变换过程中坐标变化规律的异同，从中领悟知识并加深记忆。

笔者在初中数学课堂教学中长期坚持对学生进行学法指导，让学生知其然，也知其所以然，使学生形成一定的学习能力，并从根本上掌握学习数学的方法，收到了很好的教学效果。

参考文献：

[1]《中国校外教育》（下旬刊）2010（9）.

[2]《中国校外教育.高教》2011）9）.