密度泛函理论研究MN@H2O(M=Ga, Ge, In, Sn, Sb; N=M, Al)团簇的特性

雷嘉乐, 史顺平, 张金宇, 王天科, 马 磊, 闫 珉

(成都理工大学 地球物理学院物理系， 成都 610059)

1引 言

传统化石燃料燃烧导致全球范围内二氧化碳浓度升高而产生的环境问题成为全球的主要环境问题之一[1], 为了达到低碳的目的, 未来理想的能源是低碳甚至无碳的可再生能源[2-4]. 氢气燃烧后得到的产物是水, 恰恰符合低碳这一特点.然而, 大规模使用氢能需要解决两个关键问题, 即氢气的大规模生产及其储存运输. 目前使用最为广泛的制氢方法是甲烷蒸汽转化法(SMR)[2], 其原料是天然气, 在反应中生成二氧化碳成为其致命缺陷. 因此, 通过一次清洁能源(如太阳能, 水能等)转换获取氢能成为迫切需求, 而通过离解水得到的产物燃烧后仍然是水, 既可以使原料循环利用, 同时也是绿色低碳的, 获得一种高效实惠离解水的办法前景诱人. 可以利用太阳能或水能发电从而电解水来获得氢气, 以及生物质转化技术, 或者直接利用光催化剂光解水[5]. 前者进行了能源的二次转换, 不可避免地产生了消耗, 同时也增加了成本, 因此后者的研究潜力更大, 从而寻找一种高效的光催化剂成为必要.

对于光催化剂的研究由来已久, 最早可以追溯至1921年, Renz等人报道了TiO2, CeO2, Nb2O5和Ta2O5在有机物存在的条件下, 通过光照, 这几种氧化物的量将会减少, 并转变为其他物质, 这为后来的光催化剂研究奠定了基础[6]. 直到由日本科学家Fujishima和Honda[7]发现的Fujishima-Honda效应使光解水成为了可能. 至此以后, 一大批科学家投入了寻找光催化剂的行列[8-20]. 而其主要研究的光催化剂是半导体催化剂, 以及含有d0或d10组态电子层的金属氧化物, 金属硫(氧)化物, 金属氮(氧)化物, 如TiO2, ZnO等. 尤其是TiO2由于其强氧化性及光透明度等特性被广泛地进行了研究[8, 17-20]. 它们可以有效地利用紫外光, 但却无法利用占太阳能大部分的可见光.目前为止还未找到一种能有效利用可见光的催化剂, 且绝大多数的金属氧化物, 氮化物及硫化物光催化剂都由具有d10或d0组态的金属元素构成[5]. 对于d10组态的元素, Sato等人研究发现在RuO2做辅助催化剂的条件下具有d10组态的p区金属元素的金属氧化物(如ZnGa2O4, Zn2GeO4, SrIn2O4和SrSb2O7等[9-13])对于光解水具有极大促进作用. Zou等人也对d10组态元素在光催化领域的作用进行了一系列研究[14-16]. 因此, 研究d10组态元素的物理及化学性质对了解金属氧化物的特性有很大帮助. 在光催化分解水的过程中, 表面反应位点的构建依赖于光催化剂表面的活性位点以及表面积[5, 6], 而团簇恰恰具有特殊的表面性质[21], 从理论上已经验证其为一种良好的催化剂[22-24], 由于团簇具有许多特殊的性质, 其研究涉及到原子分子物理, 凝聚态物理, 胶体化学等多个学科, 并且在材料, 能源, 催化等领域得到了良好的应用[25]. 在众多的氧化物中, d10组态的元素如Ga, Ge, In, Sn和Sb在金属氧化物催化剂中有大量的研究, 也是良好的离解水的催化剂. 而其对应的团簇也被很多研究者进行了研究, 得到了它们的结构及电子性质, 为氧化物中d10组态的元素提供大量的理论数据[26-31]. 为此, 我们选择了Ga2, Ge2, In2, Sn2, Sb2五种二聚物作为研究对象, 并寻找其最稳定结构, 在此基础上, 分析它们与水分子的相互作用.

而对于团簇催化离解水或与水分子相互作用已有前人做出研究. 在理论水平上, Meng等人[32]研究了水分子在由XAs(X=Si, Ge, Sn)构成的2D表面材料上的分解作用, 发现其具有良好的应用前景. 金蓉等人[33]研究了VOx与水分子形成的团簇的稳定结构等特性以及计算了结构和频率等. 在实验水平上, Roach等人通过研究铝团簇与水分子的相互作用, 发现在快速流动反应堆中利用多碰撞条件, 水分子可以在Al16-, Al17-和Al18-阴离子的催化作用下分解出H2[24]. 因此, Al元素的存在能加大氢气的产生, 本文在原来五种二聚物中替换一个原子为铝原子, 进一步研究了 GaAl, GeAl, InAl, SnAl, SbAl五种二聚物以及他们与水分子形成的团簇的最低能量结构, 计算了它们各自的离解能, 并分析它们与水分子的相互作用.

2计算方法

在本文中我们采用了密度泛函理论(DFT)中的B3LYP, B1B95, B3PW91, B3P86和PBE1PBE五种方法. 其中, 三参数的方法B3LYP, B3PW91和B3P86由Becke的三参数交换泛函(B3)[34]分别与泛函LYP[35], PW91[36]和P86[37]结合得到. 同时, 我们还使用了其他两个单参数混合泛函, 其中B1B95同样是由Becke提出[38], PBE1PBE是由Perdew, Burke和Ernzerhof三种泛函混合而成[39].

为了优化计算结果, 我们使用了六种不同的基组, 分别为LANL2DZ, CEP-121g、SDD, 6-31++G(3df, 3pd), 6-311++G(3df, 3pd)和6-31G(d, p). 对于二聚物Ga2, Ge2, In2, Sn2, Sb2, GaAl, GeAl, InAl, SnAl和SbAl, 我们采用LANL2DZ, CEP-121g和SDD三种不同的基组. 对于H2O, 我们采用LANL2DZ, SDD, 6-31++G(3df, 3pd), 6-311++G(3df, 3pd)和6-31G(d, p)五种不同的基组. LANL2DZ[40-42]由洛斯阿拉莫斯国家实验室提出, 在考虑了标量的相对论效应后, 其价电子被双Zeta基处理. CEP-121g[43-45]由Stevens提出, 计算时把自旋轨道效应取平均值. 而SDD[47, 48]在计算时以准相对论效应的MWB形式考虑. 6-31G[49, 50]和6-311G[51, 52]均是劈裂价键基组(Spilt Valence Basis Set), 即将价层电子的原子轨道用3个基函数来表示. 6-31G(d, p)是在6-31G的基础上, 对非氢原子添加1个极化函数的同时, 对氢原子添加1个p极化函数. 在6-31++G(3df, 3pd)和6-311++G(3df, 3pd)中, “++”表示在6-31G的基础上对所有原子添加弥散函数. (3df, 3pd)表示对非氢原子添加3个极化函数和1个具有更高角动量的f极化函数, 同时, 对氢原子也添加3个p极化函数和1个d极化函数.

我们所有的计算均是在Gaussian09 软件包下完成的.

3结果与讨论

3.1Ga2, Ge2, In2, Sn2和Sb2

利用五种方法结合三个基组, 我们计算了Ga2, Ge2, In2, Sn2和Sb2二聚物在不同的多重自旋态下最稳定结构的键长Re(Å), 离解能De(eV) (De=2E(X) -E(X2))以及频率ω (cm-1), 分别如表1, 2和3所示, 并对Ga2、Ge2、In2、Sn2和Sb2二聚物的计算结果与已有的实验数据进行对比.

对于Ga2来说, 其键长未找到实验值, 我们使用的五种方法和三个基组计算的结果在2.44-2.70 Å之间, 差别不大, 对于离解能来说, 实验值为1.4 eV[56], 最接近的是五种方法结合CEP-121G基组的结果, 对频率来说, 实验值为165 cm-1[56], 最接近的是五种方法结合SDD基组的结果. 对于Ge2来说, 键长的实验值为2.44 Å, 五种方法结合三种基组计算的值在2.33-2.37 Å之间, 都接近实验值, 离解能的实验值为2.70±0.07 eV[57, 58], 除了B1B95/LanL2DZ差别较大外, 其余都差别不大, 频率的实验值为286±5 cm-1[57, 58], 除了B1B95/LanL2DZ差别较大外, 其余都差别不大. 对于In2来说, 键长的实验值为2.83 Å[53], B1B95/CEP-121G, B3LYP/ CEP-121G, B3PW91/ CEP-121G和B3P86/ CEP-121G的结果与实验值差别较大, 其他都较接近, 离解能的实验值为0.972 eV[59]和1.002 eV[60], CEP-121G对应的五个结果都大于实验值, 而B1B95/LanL2DZ对应的结果小于实验值, 其它的都接近实验值, 频率的实验值为118.0 cm-1[63], 除了PBE1PBE/ CEP-121G的值大于实验值之外, 其它的都接近实验值. 对于Sn2, 键长的实验值为2.75 Å[54], 最接近的结果是B3P86/CEP-121G, 其余的结果都差别不大, 离解能的实验值为1.91-1.92 eV[61], PBE1PBE/LanL2DZ的计算结果最为接近, 频率的实验值为190 cm-1[54], 我们计算的结果都比较接近实验值. 对于Sb2来说, 键长的实验值为2.342 Å[55], 除了B3P86/CEP-121G的结果与实验值差别较大外, 其余都较接近实验值, 离解能的实验值为1.56 eV[62], PBE1PBE/CEP-121G, B1B95/CEP-121G, B3PW91/ CEP-121G和B3P86/CEP-121G的结果都偏离了实验值, 频率的实验值为270 cm-1[55], 五种方法结合三个基组的结果与实验值都较接近. 综上, 每一种方法及基组对应于Ga2, Ge2, In2, Sn2和Sb2二聚物时, 实验值与我们理论计算的结果各有优势, 但为了能够同一种方法和基组对研究对象，我们在不同方法和基组对之间进行比较. 通过比较, 我们发现B3P86/SDD计算得到的结果接近实验值. 于是, 我们利用方法B3P86在SDD基组水平上优化了这十种二聚物的结构.

3.2GaAl、GeAl、InAl、SnAl和SbAl

利用五种方法结合三个基组, 我们又计算了GaAl, GeAl, InAl, SnAl和SbAl五种二聚物的键长Re(Å), 离解能De(eV) (De=E(X)+E(Al)-E(XAl))以及频率ω (cm-1), 计算结果分别如表1, 2和3所示. 对于GaAl, GeAl, InAl, SnAl和SbAl五种二聚物, 我们未能找到相关的实验数值. 因此, 我们讨论当更换一个原子为铝原子之后, GaAl, GeAl, InAl, SnAl和SbAl跟Ga2, Ge2, In2, Sn2和Sb2的键长Re(Å), 离解能De(eV), 以及频率ω(cm-1)之间的变化. 虽然我们使用了五种方法和三个基组计算结果, 由于在3.1中, 已确定B3P86方法结合SDD基组计算结果更接近实验值, 因此, 本节我们主要讨论在B3P86方法结合SDD基组得到的结果之间进行对比.

对GaAl而言, 跟Ga2相比, 两者的键长都为2.55 Å, 几乎没有变化, GaAl的离解能为1.17 eV, 相比Ga2的1.12 eV, 略有增加, 而频率的变化非常明显, GaAl的频率为251.3 cm-1, Ga2的频率为186.6 cm-1. GeAl的情况有所不同, 它的键长为2.55 Å, 而Ge2的键长为2.35 Å, 即键长增加了, 但频率和离解能跟Ge2相比, 都降低了. 而InAl的情况与GeAl的恰好相反, 也就是说, 它的键长相比In2, 降低了, 但频率和离解能跟In2相比, 都增加了. 当一个Sb原子被一个Al原子替换时, 其键长增加了0.24 Å(SbAl的键长为2.76 Å，Sn2的键长为2.52 Å), 相应的离解能则降低了0.54 eV(SbAl的离解能为2.00 eV，Sn2的离解能为2.54 eV), 但频率却增加了42.3 cm-1(SbAl的频率为233.3 cm-1, Sn2的频率为191.0 cm-1). 对于SnAl而言, 与Sn2相比, 其键长, 离解能和频率的变化情况跟SbAl相似, 即键长和频率增加了, 离解能降低了.

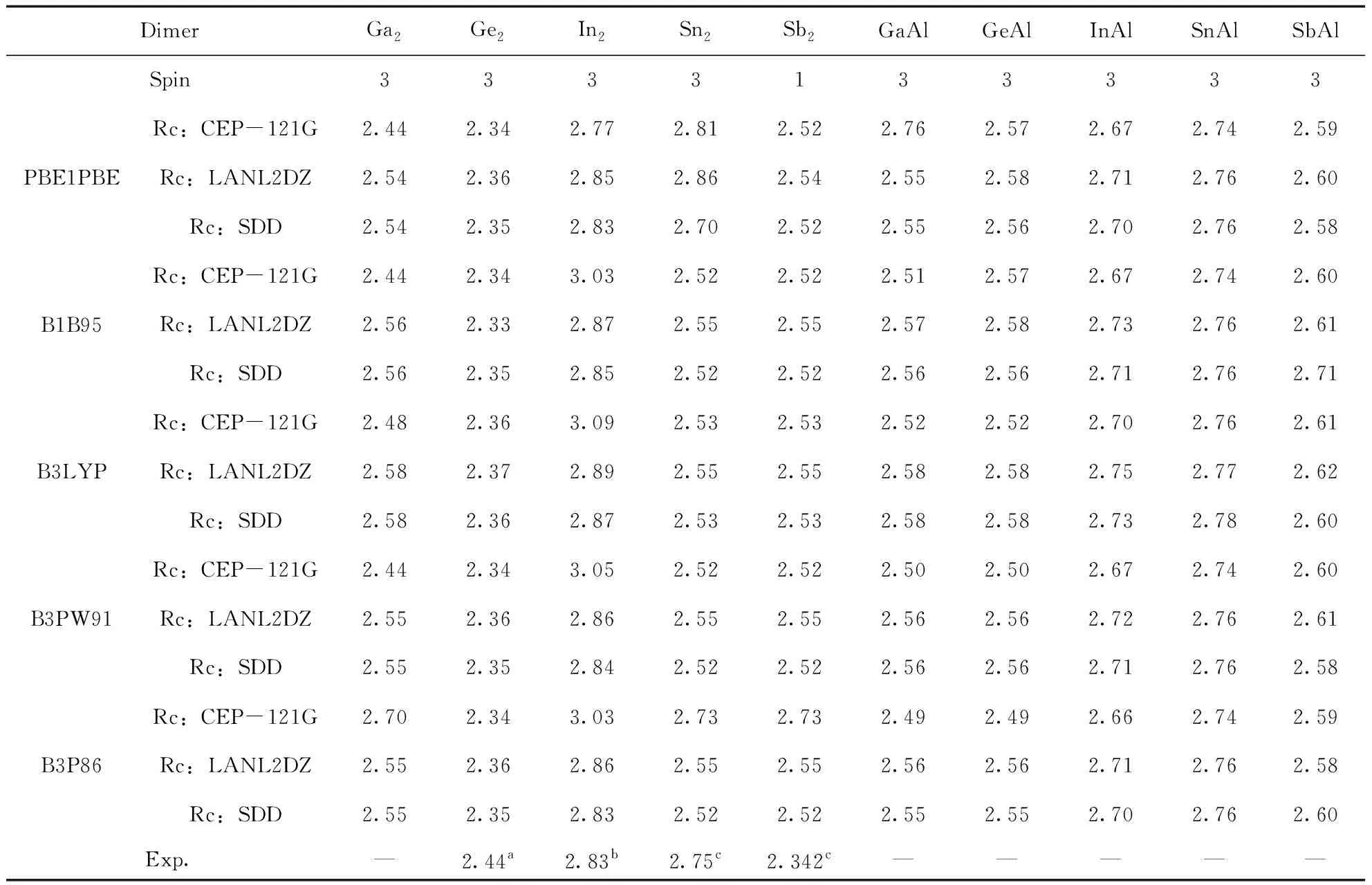
表1 二聚物Ga2, Ge2, In2, Sn2, Sb2, GaAl, GeAl, InAl, SnAl和SbAl的自旋多重度, 键长Re(Å)及相应的实验值.

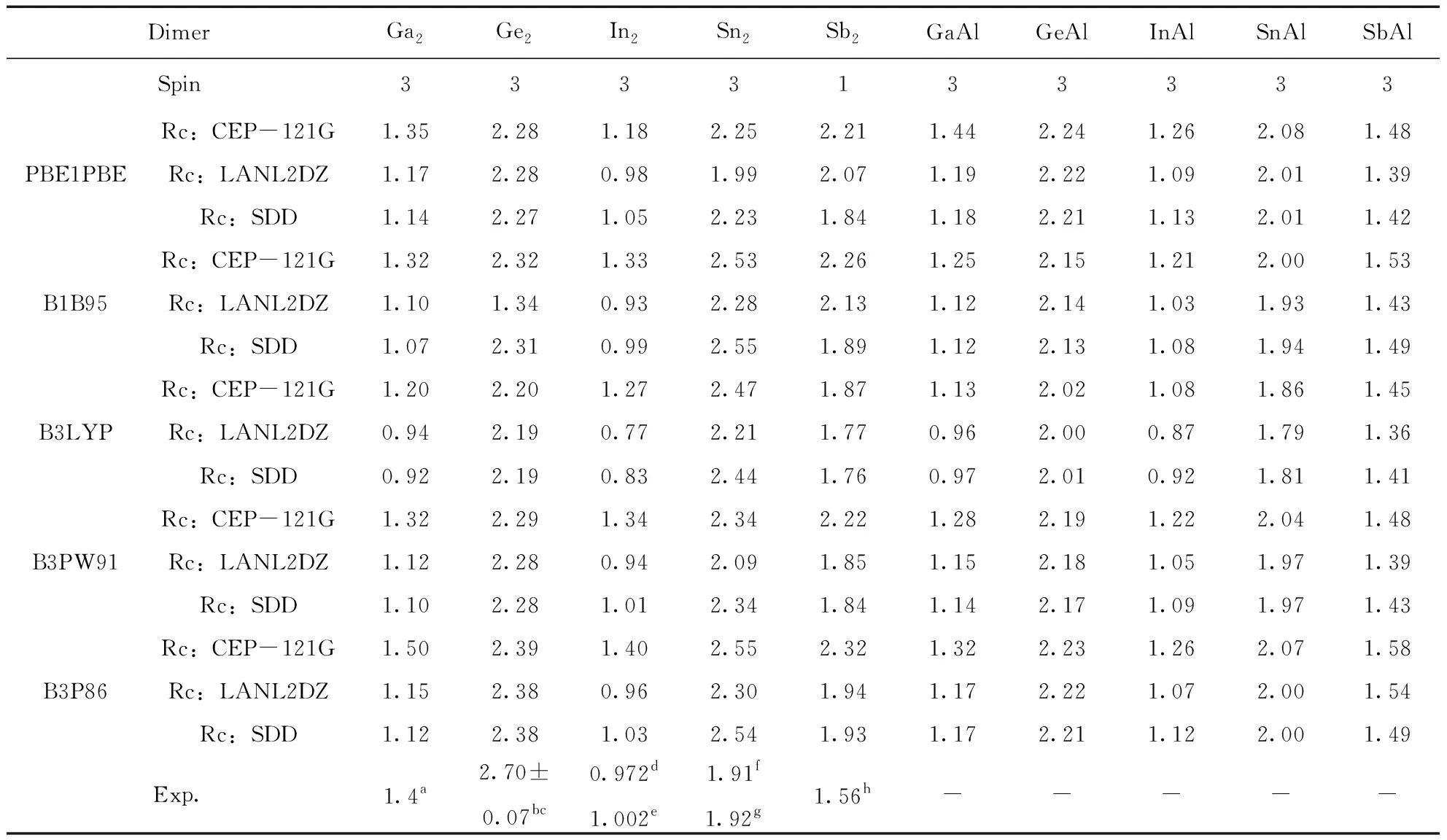
表2 二聚物Ga2, Ge2, In2, Sn2, Sb2, GaAl, GeAl, InAl, SnAl和SbAl的离解能De(eV)及相应的实验值.

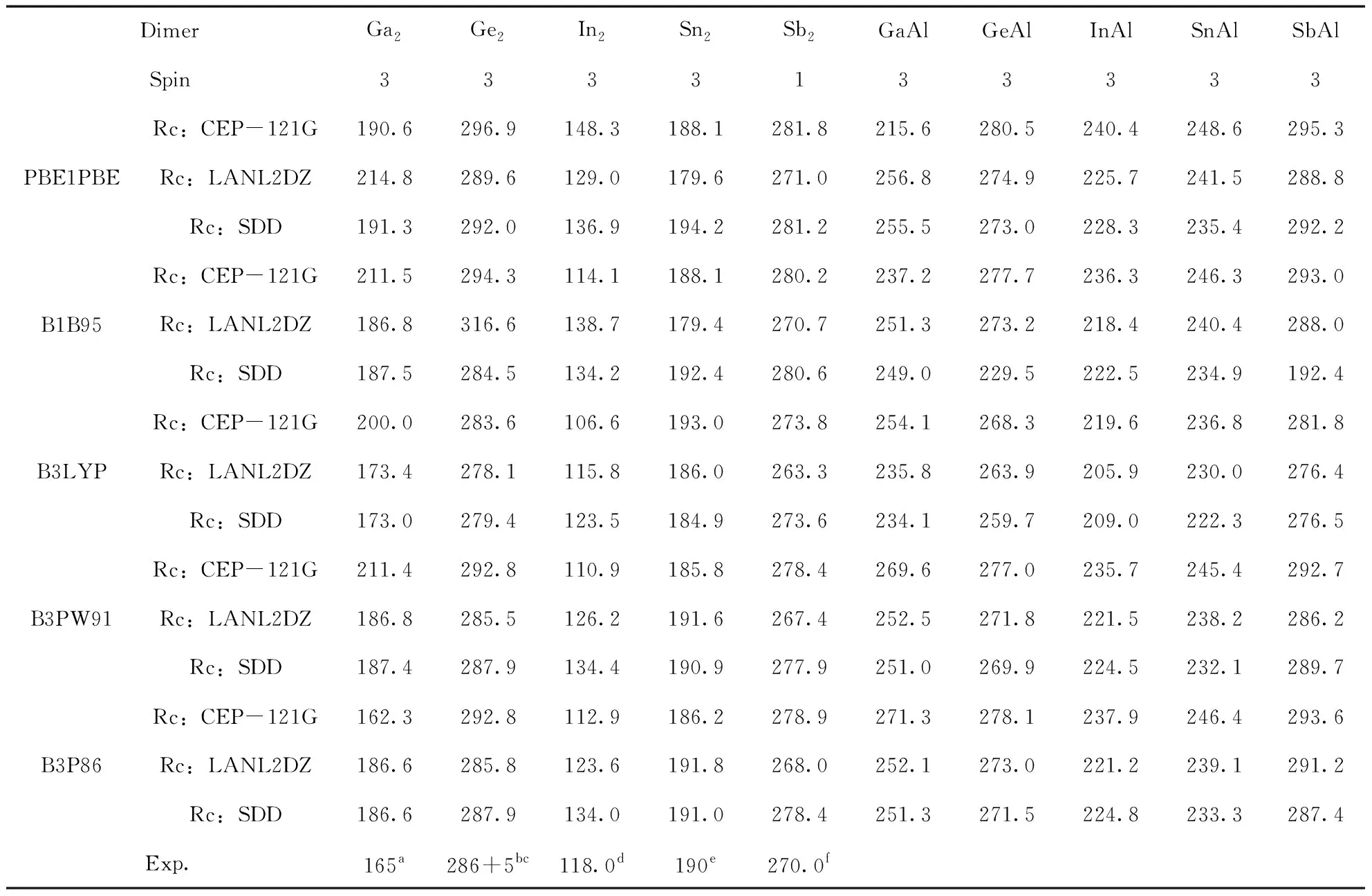
表3 二聚物Ga2, Ge2, In2, Sn2, Sb2, GaAl, GeAl, InAl, SnAl和SbAl的频率ω(cm-1) 及相应的实验值.

3.3H2O

为了研究二聚物与水分子的相互作用, 我们需得到水分子的能量. 于是我们运用B3P86, P3LYP和B3PW91三种方法结合6-31++G(3df, 3pd), 6-311++G(3df, 3pd), 6-31G(d, p), Lanl2DZ和SDD 五种基组优化了水分子的结构, 得到其最稳定结构的频率, 键长, 键角, 并与已有的实验值进行了比较, 如表4所示. 对于H2O而言, 实验值的H-O键键长为0.957 Å[64], Lanl2DZ和SDD基组得到的结果高于实验值, 其余基组的结果接近实验值. 实验得到的∠HOH=104.5°[64], B3P86/6-31++G(3df, 3pd), B3P86/6-311++G(3df, 3pd), B3PW91/6-31++G(3df, 3pd), B3PW91/6-311++G(3df, 3pd)计算得到的结果最接近实验结果, 对于三个频率来说, 实验得到的频率依次为1648.5, 3832.2和3942.5cm-1[64], P3B86/6-311++G(3df, 3pd)计算得到的结果1628.3, 3848.4和3949.8cm-1最为符合. 因此本文选择P3B86方法6-311++G(3df, 3pd)基组来优化水分子的结构.

3.4X2H2O及XAlH2O (X=Ga、Ge、In、Sn和Sb)

在3.1中, 我们确定了计算Ga, Ge, In, Sn, Sb和Al原子的体系是B3P86/SDD,在3.3中, 我们确定了B3P86方法6-311++G(3df, 3pd)基组来优化水分子的结构, 因此, 在该节中, 我们采用B3P86方法对X2H2O及XAlH2O(X=Ga, Ge,In, Sn, Sb和Al)进行计算, 对Ga, Ge, In, Sn, Sb和Al而言, 我们采用的是SDD基组, 对H2O来说, 我们采用的是6-311++G(3df, 3pd)基组. 基于以上方法和基组, 我们优化了X2H2O及XAlH2O的结构.

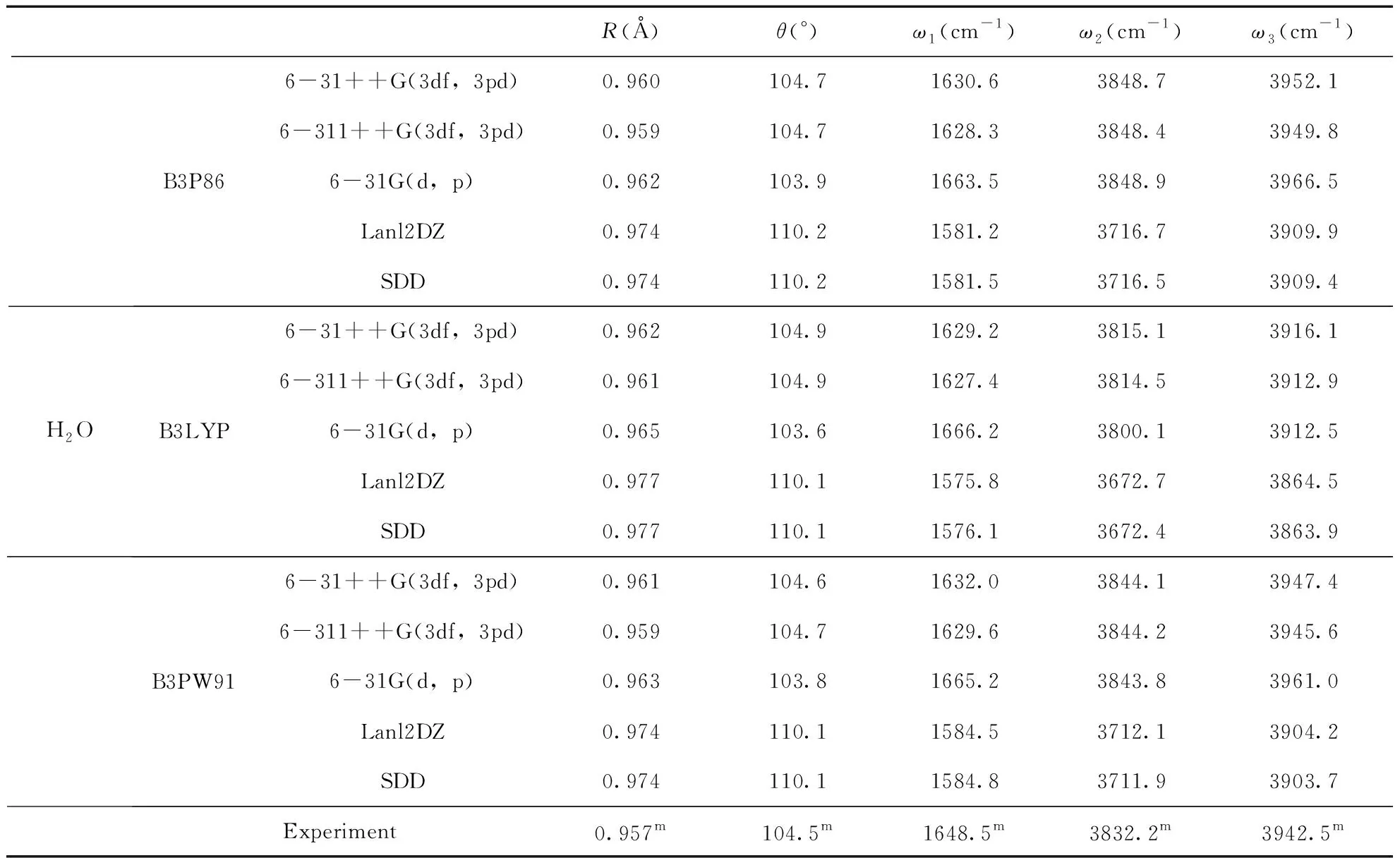
表4 水分子的平均键长R(Å), ∠HOH键角θ(°)和频率ω1(cm-1), ω2(cm-1)和ω3(cm-1)及相应的实验值.

3.4.1X2H2O(X=Ga, Ge, In, Sn和Sb)

对X2H2O(X=Ga, Ge, In, Sn和Sb), 我们优化了它们的结构, 如图1所示. 对于X2H2O体系, 我们将X-X, X-O, X-O, H-O, H-O五个键长, 能量E(a.u.)和H-O-H键角θ(°)分别列在表5中. 对于X2H2O体系, 它们的自旋多重度均为1.

对于Ga2H2O, Ga-Ga键长在加入水分子之后由2.55 Å拉长到2.90 Å, 表明Ga-Ga键更容易断裂. 两个Ga-O键的键长分别为2.59和2.77 Å, 两个H-O的键长分别为0.96和0.97 Å, 与纯的水分子相比, 其键长变化不大(H2O的键长为0.959 Å), 并且通过键角对比发现, 水分子的键角θ由104.7°变为108.05°, 键角变大了. 对于Ge2H2O, Ge-Ge键长也由2.35 Å变长为2.45 Å, 表明添加一个H2O后, Ge-Ge也容易断裂. 两个Ge-O的键长相等, 都为2.47 Å, 同样的, 两个H-O键的键长也相当, 均为0.96 Å, 跟纯水分子相比, H-O键没有变化, 但是, 其键角由104.7°增大到109.02°. In2H2O和Sn2H2O的变化情况跟Ga2H2O和Ge2H2O的变化情况基本相同, 即In-In和Sn-Sn键增加了, H-O键基本没有变化, 而H-O-H键角也变大了. 但对于Sb2H2O来说, 添加一个水分子对Sb-Sb键长没有任何影响, 仍然是2.52 Å, 同样, Sb对H-O键和H-O-H键角也没有任何影响, 还是0.96 Å和104.9°.

总体来说, X2H2O(X=Ga, Ge, In, Sn和Sb)对水分子仅受轻微的影响, 即对水分子的键长影响变化不大, 键角略有增加, 除了Sb2H2O. 反而是几种二聚物受水分子影响较大, 即键长变化较大, 除了Sb-Sb键. 从结果也可以看出, Ga2, Ge2, In2, Sn2和Sb2五种团簇与水之间不能形成共价键. 其中Ge2H2O以及Sn2H2O的结构尤为奇特, 近乎轴对称的同时, 氧原子与两个Ge(或Sn)原子组成的三角形近乎为等边三角形(键角为60.33°, 60.33°, 59.34°以及58.79°, 58.65°, 62.56°). 同样, 同为第三主族的Ga以及In元素对应的Ga2H2O和In2H2O的结构也极为相似(见图1).

表5 X2H2O(X=Ga, Ge, In, Sn和Sb)团簇的键长X-X(Å), X-O(Å), X-O(Å), H-O(Å), H-O(Å), 能量E(a.u.)和H-O-H键角θ(°).

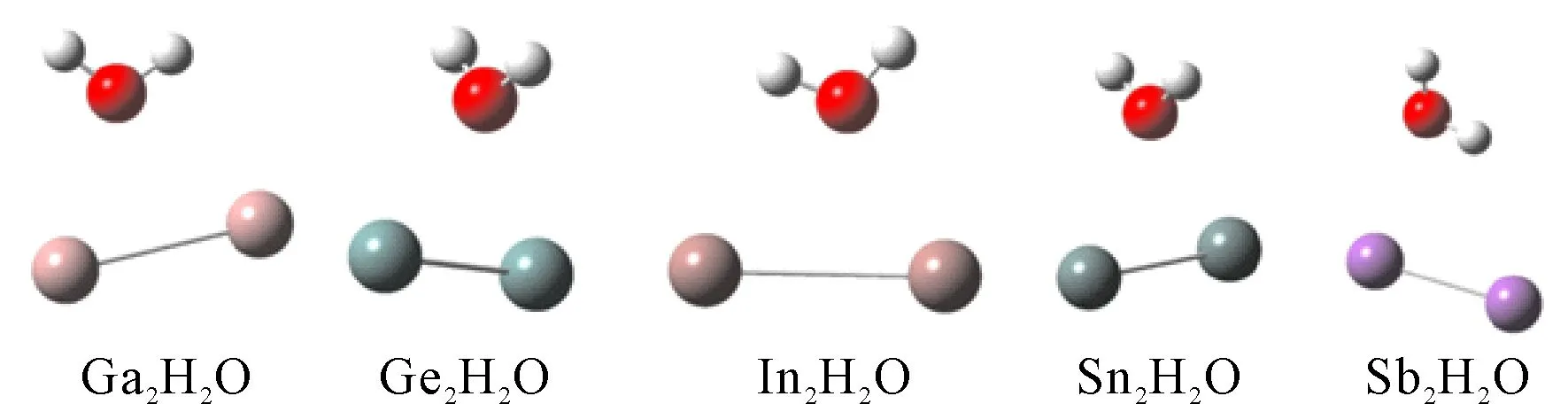
图1 团簇X2H2O(X=Ga, Ge, In, Sn和Sb)的结构.Fig. 1 The structures of X2H2O(X=Ga, Ge, In, Sn and Sb).

3.4.2XAlH2O和AlXH2O(Ga, Ge, In, Sn和Sb)

对于一个Al原子替代Ga, Ge, In, Sn和Sb之后, 我们考虑了两种吸附方式,即Al原子吸附H2O或Ga, Ge, In, Sn和Sb吸附H2O, 对Al吸附H2O, 标记为XAlH2O, 优化的结果如图2所示(第一行), 对Ga, Ge, In, Sn和Sb吸附H2O, 标记为AlXH2O, 优化的结果如图2所示(第二行). 对XAlH2O和AlXH2O团簇的X-Al, X-O, Al-O, H-O和H-O键长, 能量E(a.u.)和键角H-O-H键角θ(°)分别列在表6中. 在计算中, GeAlH2O, AlGeH2O, SnAlH2O和AlSnH2O团簇最稳定时, 其自旋多重度为2, GaAlH2O团簇在最稳定时, 自旋多重度为3, AlGaH2O, InAlH2O, AlInH2O, SbAlH2O和AlSbH2O的自旋多重度为1.

对于AlGaH2O和GaAlH2O, 无论是Al还是Ga直接吸附H2O, Ga-Al的键长均为2.89Å, 与Ga2H2O中的Ga-Ga相比, 其键长变化也较小. 当Ga吸附H2O时, Ga-O键跟Al-O键键长相差很小, 但是当Al吸附H2O时, Al-O键比Ga-O键小很多. 两者的H-O键键长都较接近, 而Al吸附H2O时的H-O-H键角比Al吸附H2O时大了1.64°. AlGeH2O和GeAlH2O, 当H2O与Ge接触时, 其Ge-Al键的键长比Ge-Ge的键长长了, 当H2O与Al接触时, 其Ge-Al键的键长与Ge-Ge的键长相接近. Ge-O和Al-O键的变化与吸附有直接的关系, Ge吸附H2O时, 其Ge-O键长较短, Al-O键较大, 当Al吸附H2O时, 结果恰好相反. 对H-O键来说, 其跟Ge2吸附及纯的H2O的键长相同. 而H-O-H键角相比Ge2H2O来说, 变小了, 但比纯的H2O的键角大. AlInH2O和InAlH2O的变化情况跟AlGaH2O和GaAlH2O是相同的. AlSnH2O和SnAlH2O的变化情况跟AlGeH2O和GeAlH2O是相同的. 对于AlSbH2O和SbAlH2O的情况跟其他四组的差别较大, Sb或Al吸附H2O时, 不管是Sb-Al键键长, Sb-O键键长, Al-O键键长, H-O键键长及H-O-H键角几乎没有变化.

总体来说, 对Ga, In和Sb三元素而言, X-Al键长在掺入了水分子之后数值变化较大, 而第四主族的Ge和Sn, 该键长变化较小, 为了更清晰地表示出来, 我们把掺入水分子前后的键长变化对比绘成了折线图, 如图3所示. 从图3的结构图可以看出, 对于XAlH2O和AlXH2O而言, 水分子吸附的原子, 该原子多数可以跟氧原子成共价键(除AlGaH2O和AlGeH2O外), 这与前面的X2H2O完全不同. 当然, 在XAlH2O和AlXH2O中水分子的变化同样不大(见表4和6).

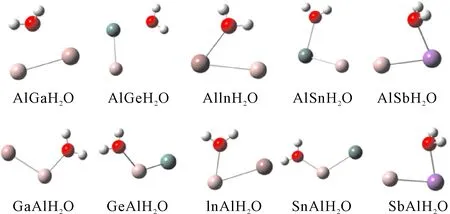
图2 团簇XAlH2O(X=Ga, Ge, In, Sn, Sb)结构.Fig. 2 The structures of XAlH2O(X=Ga, Ge, In, Sn, Sb) clusters.

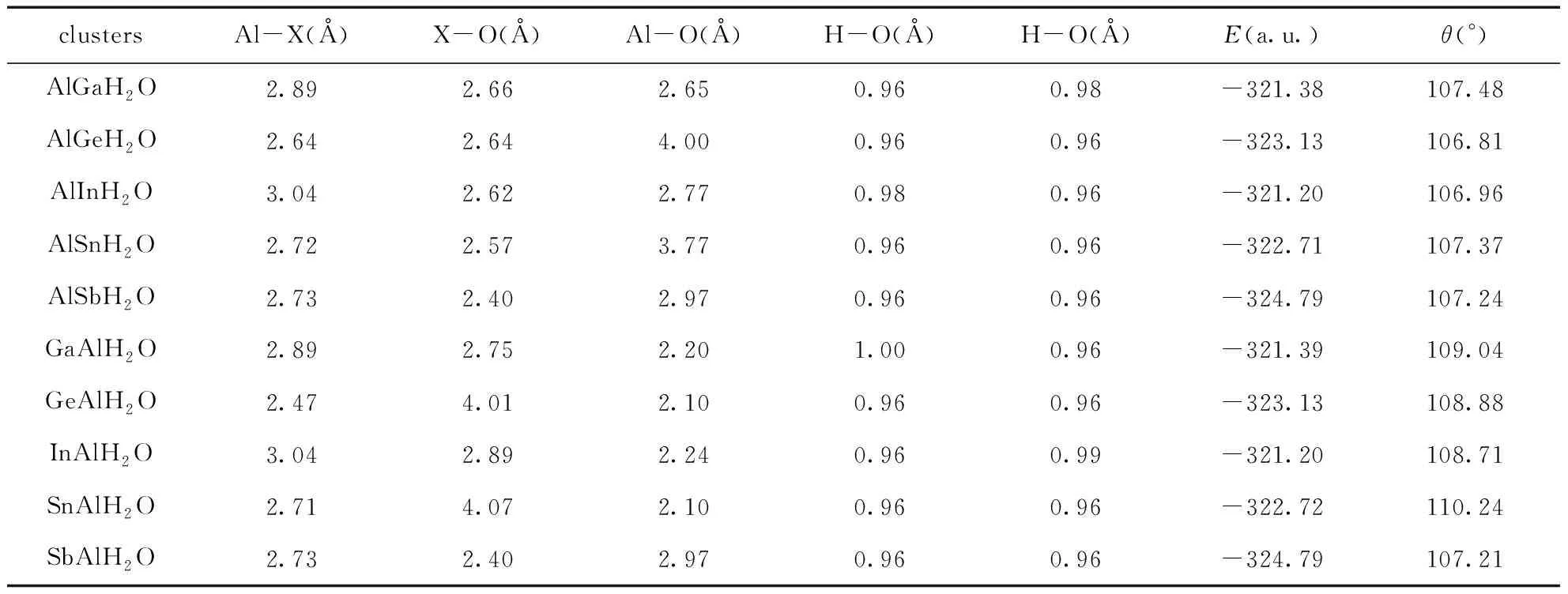
表6 XAlH2O及AlXH2O(X=Ga, Ge, In, Sn和Al)的团簇键长Al-X (Å), X-O (Å), Al-O (Å), H-O(Å), H-O(Å), 能量E(a.u.)和H-O-H键角θ(°)

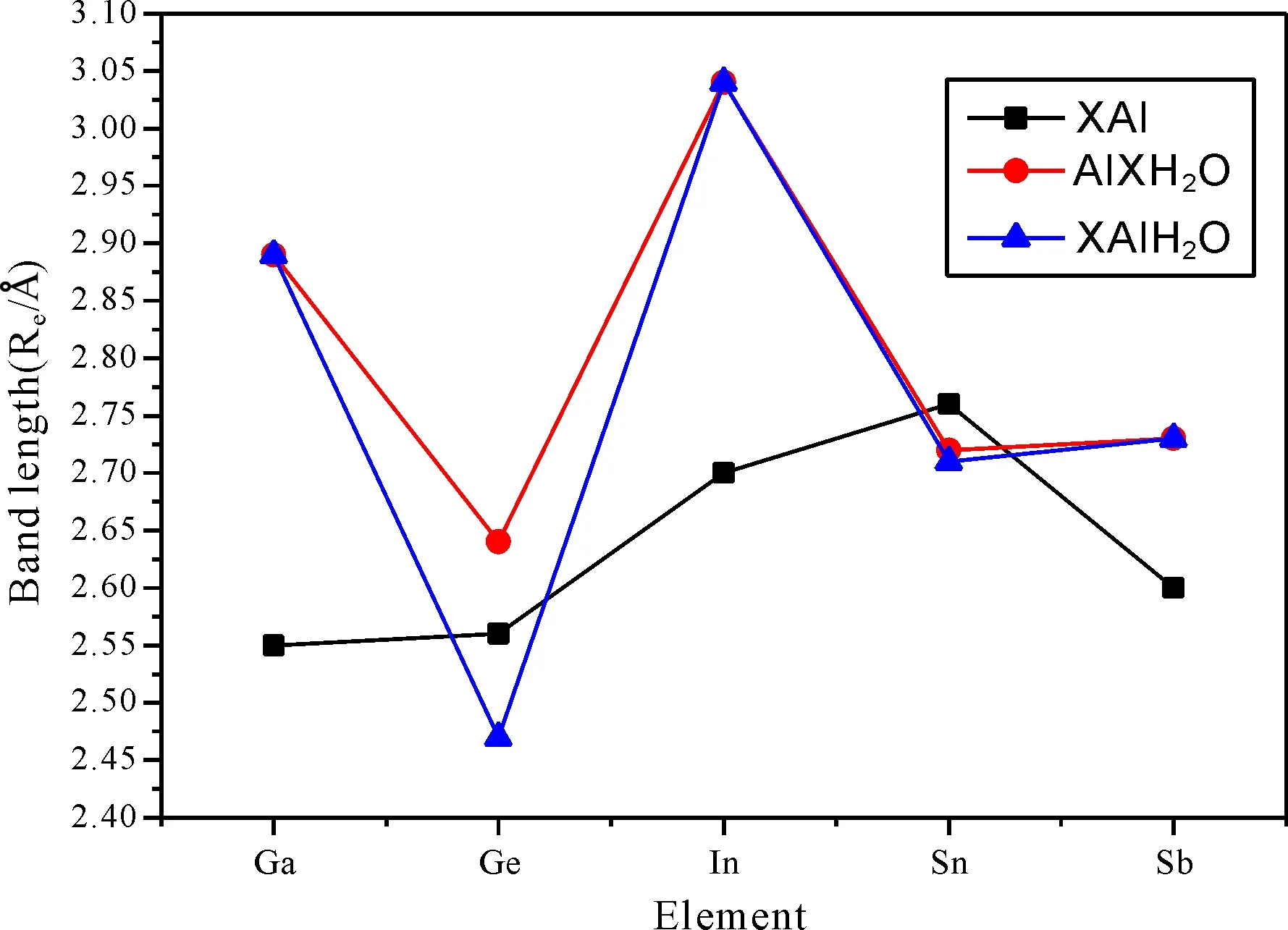
图3 掺入水分子前后二聚物键长X-Al (Å)变化情况.Fig. 3 The changes of bond lengths X-Al (Å) before and after absorption of water molecules.

3.4.3X2H2O, XAlH2O和AlXH2O(Ga, Ge, In, Sn和Sb)的吸附能

在确定了X2H2O, XAlH2O和AlXH2O团簇的稳定构型后, 进一步计算了水分子吸附能Ea, 其结果如表7所示. 吸附能的计算公式如下:

Ea=E(X2)+E(H2O)-E(X2H2O)

(1)

Ea=E(XAl)+E(H2O)-E(XAlH2O)

(2)

式中E表示各个体系的能量.

为了更好地观察水分子在不同二聚物上吸附能的变化, 我们把表格7中的数据制成如图4所示的折线图. 从图4可以看出, X2H2O, XAlH2O和AlXH2O团簇的吸附能随着Ga, Ge, In, Sn和Sb的变化, 出现振荡行为, 即Ge和Sn的吸附能要高于其他三个的吸附能. 然而, 当将一个原子换为Al之后, 振荡现象发生了变化, 即Ge和Sn的吸附能低于其他三个的吸附能, 说明Al的掺入改变了Ge和Sn的吸附能. 当把位于第三主族的镓, 铟以及位于第五主族锑的二聚物的一个原子换成铝后, 水分子在其上的吸附能并没有太大的变化, 且水分子在这几种二聚物上的吸附能几乎相同. 但位于第四主族的锗和锡的二聚物的结果则完全相反, 在本来吸附能更高的情况下, 把一个元素变为铝元素之后, 水分子在其上的吸附能下降明显. 另外, 从图4可以看出, H2O吸附在Ga和Sn, 吸附能微弱的增大, 吸附在Al上, 吸附能微弱的降低, 而对于Ge, In和Sb来说, H2O吸附在Ge, In和Sb或Al上时, 吸附能没有明显的变化, 因此, 我们得出H2O的吸附位置不影响吸附能的变化.

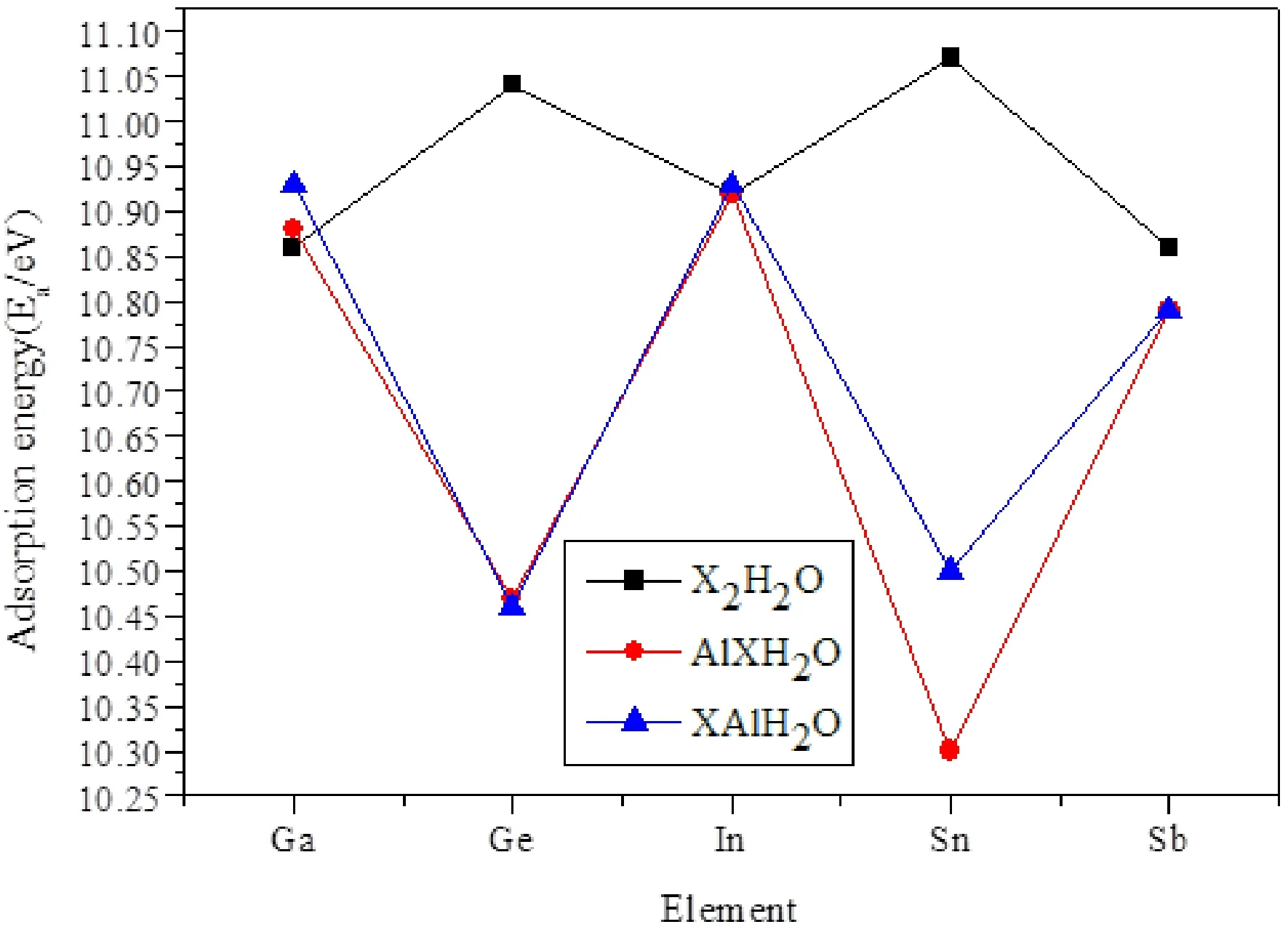
图4 X2H2O、XAlH2O和AlXH2O团簇的吸附能.Fig. 4 The absorption energies Ea(eV) of X2H2O, XAlH2O and AlXH2O clusters.

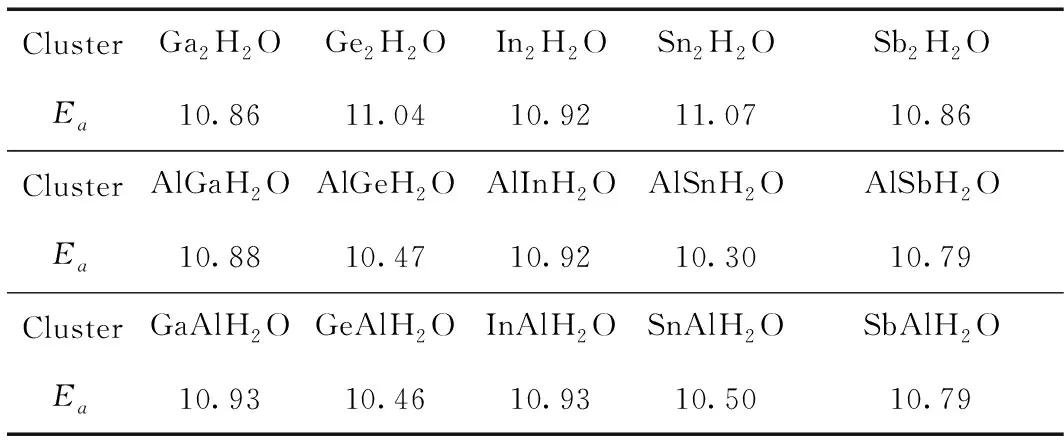
表7 X2H2O, XAlH2O和AlXH2O团簇的吸附能Ea(eV).

4结 论

本文采用密度泛函理论计算了X2及XAl (X=Ga, Ge, In, Sn和Sb)的结构, 得到了各个二聚物的频率和能量. X2的计算结果与已有的实验值进行了比较, 发现在B3P86/SDD下得到的结果较为接近实验值. 当Al原子替换一个Ga或In时, 离解能升高了, 当Al原子替换一个Ge, Sn或Sb时, 离解能增加了. 采用B3P86, P3LYP和B3PW91三种方法结合6-31++G(3df, 3pd), 6-311++G(3df, 3pd), 6-31G(d, p), Lanl2DZ和SDD优化了H2O的结构, 得到了频率, 能量及H-O键键长, 并于已有实验值进行了比较, 发现P3B86方法结合6-311++G(3df, 3pd)基组的结果更接近实验值. 进一步采用B3P86方法，SDD和6-311++G(3df, 3pd)基组优化了X2H2O以及XAlH2O的结构, 得到其能量, 并计算了吸附能. Ge和Al以及Sn和Al所构成的体系与水分子具有更高的反应性, 即在与水分子反应时, 相较于其他几种体系(单独的Ga, Ge, In, Sn, Sb及Ga和Al, In和Al, Sb和Al)具有优越性.