激光场中锂原子发射的电离阈值以下低阶谐波的研究

张启迪， 李鹏程， 赵松峰， 周效信

(西北师范大学物理与电子工程学院, 兰州730070)

1引 言

自上世纪80年代末从实验上发现气体在激光场中发射高次谐波(High-order harmonic generation,HHG)现象以来[1,2]，人们对高次谐波的研究产生了极大的兴趣[3-6]，一方面是需要理解高次谐波的发射机理[7]，另一方面，高次谐波是合成超短阿秒脉冲的重要途径[8].当强激光场与原子分子相互作用时,所发射的高次谐波是一种非线性现象,对于平台区域的高次谐波，其产生机理可用半经典的三步模型[3]来解释：当原子在强激光场的驱动下，激光场和原子实的库仑场联合作用形成一个势垒,原子中的价电子会隧穿这个势垒而进入到连续态，处于连续态的电子会被激光场加速，当激光场反向时，电子会改变方向并向原子实加速运动,从激光场获得能量，当电子返回原子实附近时,与原子实复合回到基态，从而将电子从激光场获得的能量以光子的形式辐射出来，即发射高次谐波.对于处在平台区域的高次谐波可以很好地用三步模型加以解释.近年来,人们对电离阈值以下的低阶谐波(Low-order harmonic generation, LOHG)进行了研究,研究结果表明,低阶谐波的发射要比平台区域的谐波发射机理复杂的多,不能用三步模型来解释,因为低阶谐波牵涉到原子束缚态在激光场中的性质, Camp 等人[9]研究了氦原子阈值附近谐波的提高，他们发现谐波的提高主要来源于原子基态和发生Stark移动的激发态之间的多光子共振，Beaulieu等人[10]研究了阈值附近氩原子谐波的结构. 观察到除了通常的奇次谐波外，还存在着一些侧峰，并且确定原子激发态对这些侧峰的形成起着重要的作用，Li等人[11]通过同步压缩变换技术(Synchrosqueezing transform,SST)[12]和半经典分析研究了近阈值和阈值以下Cs原子低阶谐波的性质，Xiong等人[13]以氢原子为例，研究了这些低阶谐波侧峰形成的原因，最近，我们对He原子低阶谐波的侧峰进行了研究[14],结合同步压缩解释了低阶谐波的侧峰结构由两部分组成，并且部分侧峰和主峰之间的间隔可以用来估算原子激发态在激光场中的最大Stark移动.

对于其它原子如碱金属原子在激光场低阶谐波的性质是否也存在侧峰结构以及侧峰的性质并没有结论，虽然文献[11]研究了碱金属原子Cs的低阶谐波，其侧重点是低阶谐波发射的动力学过程，对碱金属原子低阶谐波的侧峰结构并未给与关注，本文研究了碱金属的锂原子在强激光场中电离阈值以下低阶谐波出现的侧峰性质，利用锂原子的精确模型势，通过数值求解锂原子在激光场中的三维含时薛定谔方程,计算了锂原子的低阶谐波谱,结果也出现了一些谐波的侧峰结构,并利用SST技术对这些侧峰性质进行了分析.

2理论方法

锂原子属于多电子原子，通常情况下可以把锂原子作为准单电子体系进行处理，即由原子实和最外层的一个价电子组成.当激光场不是太强的情况下，原子实作为冻结核来处理, 仅考虑价电子在激光场中动力学过程. 在激光场中，该价电子受到原子实和激光场的共同作用而运动，原子实对价电子的作用可以用一个精确的模型势表示，该模型势可以表示为[15](如没有特别说明,以下均采用原子单位)：

Crexp(-βr))

(1)

式中的相关参数为：z=3,α=7.90875,β=3.90006,C=10.321.在偶极近似下，激光对价电子的相互作用可以表示为：

V(r,t)=-E·r=-E0zf(t)sinωt

(2)

式中E0是激光场的电场分量，f(t)是激光脉冲的包络.这样，锂原子中价电子在激光场的运动可以用下述的三维含时薛定谔方程描述：

(3)

其中H0是锂原子的无场下的哈密顿量：

(4)

利用含时广义伪谱方法(TDGPS)[16]在球坐标下对(3)式进行数值求解, 已知t时刻体系的波函数，则t+Δt时刻的波函数可表示为：

(5)

通过对(5)式的演化，直到激光场结束，从而获得原子在激光场作用下的含时波函数,然后计算出在长度规范下原子的诱导偶极矩：

dL(t)=〈ψ(r,t)|z|ψ(r,t)〉

(6)

通过Ehrenfest定理,可获得诱导偶极加速度为：

(7)

对诱导的偶极矩或偶极加速度进行傅里叶变换，可以得到原子发射的高次谐波谱：

(8)

(9)

下文我们称由偶极矩得到的谐波称为长度形式，由偶极加速度得到谐波成为加速度形式.

为了更好地理解低阶谐波的动力学过程，我们采用同步压缩变换技术(SST)，对发射的谐波在时频空间进行分析，相对于传统的时频分析方法(如Gabor变换，Morlet变换等)，SST 方法对于能量随时间的变化的分辨率有很大提高，能够更清楚的了解低阶谐波发射的动力学过程.

3结果和讨论

首先，利用精确的模型势(1)式，通过对角化的方法，得到无场下锂原子的束缚态能级和相应波函数，所得到束缚态能级在表1中给出，表中的第一行是NIST数据库给出的数值[17]，第二行是我们利用精确的模型势得到的结果.从表中可以看出，利用模型势计算的能级与NIST中给出的结果符合得很好.

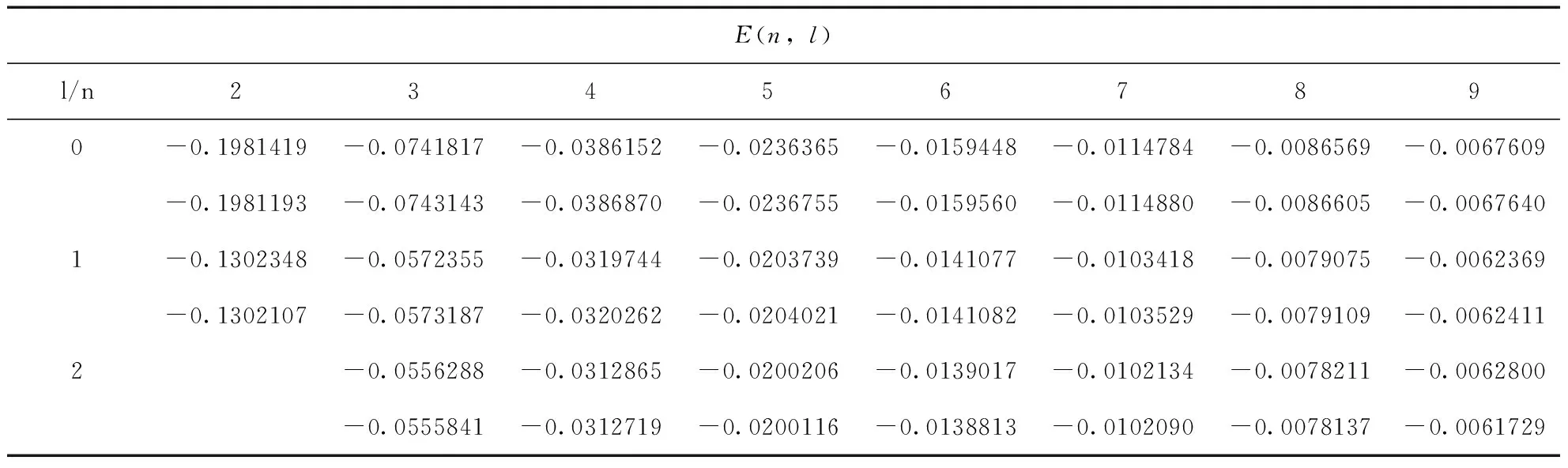
表1 锂原子的能级值(Hartree)

为了确定计算的低阶谐波的收敛性，我们对偶极矩得到的谐波和加速度得到的谐波进行了比较，在计算过程中将上面得到无场下锂原子的基态2s态作为初态，激光强度选为1.4×1012W/cm2，波长为1600nm，sin2包络，周期为25个，得到锂原子的低阶谐波，如图1所示.由图1可以看出，由长度形式和加速度形式得到地谐波符合得很好，说明我们的计算结果是可靠的.因为加速度形式得到的结果更为可靠，下面我们在分析谐波谱的性质时，均采用加速度形式的结果.

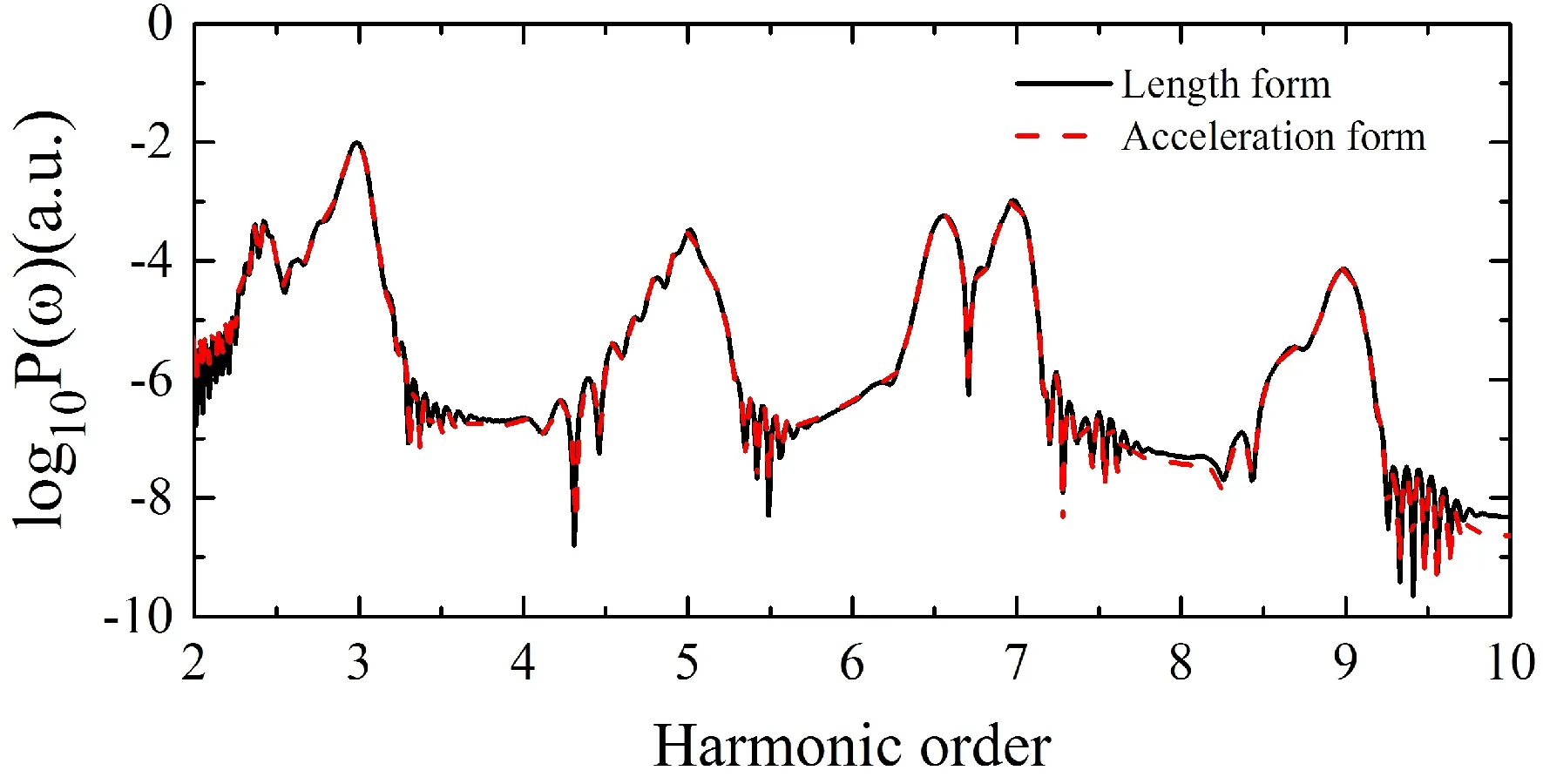
图1 锂原子长度形式谐波谱和加速度形式谐波谱的比较Fig. 1 Comparison of the low-order harmonic spectra for the length and acceleration form of Li atom

从图1还可以看出, 在电离阈值以下(即8阶以下)，除了出现奇次谐波外，在第3阶、第5阶和第7阶较低的一侧还出现了侧峰,只不过第5阶的侧峰不太明显. 对于正常发射的低阶谐波，即3、5、7……等谐波，这是由于原子在同一能级上形成的缀饰态之间的跃迁形成的，而对于侧峰部分的形成，则需要对谐波谱进行时频分析来加以理解，为此，我们对加速度形式的谐波谱进行了SST计算，计算结果在图2(b)中给出.

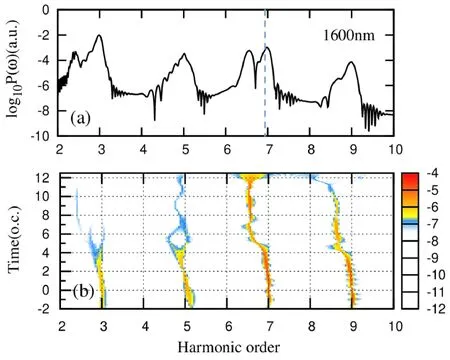
图2 激光波长取为1600nm时,(a)锂原子的低阶谐波谱，(b)相应的SST时频分析图.Fig. 2 (a) Low-order harmonic spectra of lithium atom, (b) time-frequency analysis of SST with laser wavelength is 1600nm

由图2(a)可以看出，第5阶的侧峰不太明显，图中的虚线位置是锂原子的电离阈值.而由图2(b)可以看出，第3阶和第7阶的侧峰具有不同的特点，第3 阶侧峰会随激光场结束而结束发射，因此，可以推测该侧峰主要是原子的束缚态在激光场中形成的缀饰态之间的跃迁形成的，当激光强度趋近于零时，这类跃迁也随之消失.对于第7阶谐波而言，除了在激光脉冲作用期间有谐波发射外(图中是激光脉冲的下降沿)，当激光结束后，侧峰的谐波仍有发射，说明该侧峰由两部分组成：一部分是束缚态在激光场中形成的缀饰态之间的跃迁形成的，这些缀饰态包含了能级的Stark移动；另一部分是无场下原子的激发态向基态跃迁形成的.由第7阶侧峰的位置刚好与激光结束时辐射的中心位置重合，因此该侧峰的位置与第7阶主峰的能量差反映了原子激发态的最大Stark移动.为了说明这一点，将我们在文献[14]中提出的公式应用到锂原子，其侧峰的能量满足：

(Ejp±mω+Ux)-(E2s±nω)=qħω

(9)

其中,Ejp±mω是原子激发态Ejp在激光场中的缀饰态能级,Ux是束缚态在t时刻的瞬时Stark移动,E2s±nω为原子基态在激光场中的缀饰态能级, q为非整数,qħω是侧峰的光子能量.相应的能级图如图3所示.

图3 激光场中Li原子的6p态和2s态的缀饰态能级Fig. 3 The 6p and 2s decorated state energy levels of lithium atoms in the laser field

对于通常的奇数阶谐波,是由同一个束缚态形成的缀饰态之间跃迁形成的,由于需要满足宇称守恒,因此只有奇数阶谐波产生,对于侧峰而言,是由不同的束缚态形成的缀饰态之间的跃迁产生的,其侧峰的能量反映了瞬时Stark移动,如图中的跃迁①、②、③，当激光结束时，侧峰的位置与主峰的位置之差就是激发态的最大Stark移动.对照图2(b)中侧峰的位置是q=6.6，可以推算该能级的最大Stark移动为0.4阶，对照表1中能级值，可以算出，该跃迁是由6p-2s的跃迁形成的，因此，6p态的最大Stark移动为0.4阶,相当于1.0Up (Up为电子的有质动力能). 为了确定第7阶侧峰的确就是6p-2s的跃迁，我们还可以通过原子在激发态的布居数来证明，为此，我们计算了激光脉冲将要结束时原子在np激发态的布居数，如图4所示，的确就是6p态的布居数最大，与能级差得到的结果一致.由上面分析可以看出，图2(a)中的第7阶侧峰主要来源于无场下6p-2s态之间的跃迁，其辐射的谐波能量刚好是相应跃迁能级差，由此可以估算出6p态的最大Stark移动，同时也可以看出，第3阶的侧峰则仅是缀饰态之间的跃迁产生的.

按照上面的分析,如果采用其它波长的激光脉冲驱动锂原子，当激光结束时，有可能不是6p的布居数较大，而是其它激发态的布居数较大，这时一些低阶谐波的侧峰位置就会有所不同，为此，我们使用激光波长为1800nm,激光强度仍为1.4×1012W/cm2来驱动锂原子，得到了相应的低阶谐波谱,并对这些谐波进行了SST时频分析计算，相应的结果在图4中给出.

图4 激光波长取为1800nm时,(a)锂原子的低阶谐波谱，(b)相应的SST时频分析图. Fig. 4 (a) Low-order harmonic spectra of lithium atom, (b) time-frequency analysis of SST with laser wavelength is 1600nm

由图4(a)可以看出，阈值以下的谐波，如第3，5，7阶谐波也都出现了侧峰结构，与图2不同的是当激光结束时，有两个侧峰仍在发射[见图4(b)]，按照前面分析可以看出，第5阶的侧峰纯粹是由原子的缀饰态之间的跃迁形成的，而第3阶和第7阶除了有缀饰态的贡献外，还有无场下原子的激发态向基态跃迁的贡献，根据侧峰的位置，并对照表1的能级数值，可以推出第3阶侧峰主要是锂原子的2p激发态向2s基态跃迁形成的，而第7阶的侧峰则是4p激发态向2s基态跃迁形成的.而且通过这些侧峰和相应的主峰之间的能量差，可以推算出2p激发态的最大Stark移动为0.49Up，4p激发态的最大Stark移动为0.81Up.

为了进一步确认上面根据侧峰位置结合激发态到基态能级差分析得到的结果，我们还对激光结束前的几个周期内原子在不同p激发态的布居数进行了计算，计算结果如图5所示.

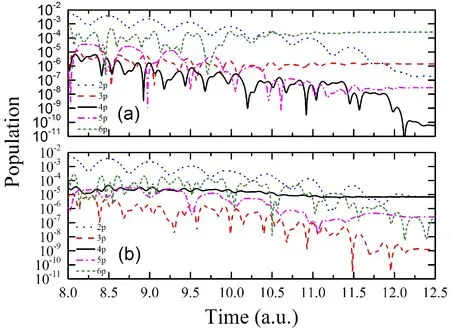
图5 锂原子在激发态的布居数. 激光波长为(a) 1600nm, (b) 1800nmFig. 5 The population of the excited states of lithium atom, laser wavelength (a) 1600nm, (b) 1800nm

由图5(a)的结果可以看出，在波长为1600nm激光驱动锂原子情况下，当激光脉冲从11.5周期到激光结束时，电子在激发态6p布居数远远高于其它激发态的布居数,因此，无场下6p激发态到基态的跃迁是主要，这正好对应图2(a)中第7阶侧峰的情况；图5(b)给出了激光波长是1800nm情况下，不同p激发态电子的布居数,当激光脉冲快要结束时,2p态和4p态的布居数远大于其它激发态的布居，因此，2p态和4p态向基态跃迁的几率远大于其它态的跃迁，这一结果刚好与能级差的分析也是一致的.

4结 论

本文在单电子近似下，利用锂原子的精确模型势，通过数值求解锂原子在激光脉冲驱动下的含时薛定谔方程,研究了锂原子在电离阈值以下的低阶谐波谱.研究结果表明，锂原子的低阶谐波除了有通常的奇数次谐波外，还会出现一些侧峰结构，利用计算精度高的同步压缩变换技术详细分析了产生这些侧峰结构的机理，分析结果表明,通过SST时频分析技术，我们能够辨认出锂原子低阶谐波侧峰结构有两类：一类是由原子的束缚态在激光场中所形成的缀饰态之间的跃迁产生的，这部分谐波侧峰会随着激光脉冲的结束而结束，其中包含了束缚态的瞬时Stark移动,另一类的侧峰既包含这些缀饰态之间跃迁的贡献，还包含无场下原子的激发态向基态跃迁的贡献，而这一部分的侧峰即使激光脉冲结束了，原子在一些激发态仍有较大的布居数，所以还有谐波的发射，利用侧峰的这一特点，可以通过计算侧峰与主峰的能量差来估算原子激发态在激光场中的最大Stark移动.