La掺杂TiO2(101)面的电子结构和光学性质的第一性原理研究

李东翔, 李瑞琴, 骆远征, 闫万珺

(1. 安顺学院数理学院, 安顺 561000; 2.安顺学院电子与信息工程学院, 安顺 561000)

1引 言

自从Fujishima和Honda[1]在1972年报道了紫外光辐照二氧化钛(TiO2)半导体材料具有光催化活性以来, 以TiO2为代表的光催化材料已得到广泛研究[ 2-5]. TiO2是一种宽带隙的半导体材料(金红石和锐钛矿分别为3.0 eV和3.2 eV), 具有优异的化学稳定性、低成本和无毒性. 因此, 它常用于污水处理、空气净化、自清洁、水的光催化分解、制氢和太阳能电池等方面[6-8]. 然而, 由于TiO2自身的带隙较宽, 所以只允许其在紫外(UV)光区域进行光催化作用. 但是, 紫外线仅仅占太阳光的4%, 而可见光约占太阳光的43%. 因此, 如何在可见光区域有效的将TiO2应用于光催化反应已经成为一个重要的研究课题.

稀土元素具有特定的电子层结构，因此它们具有优异的光学、电学、磁学和光催化性能. 目前, 利用稀土离子掺杂TiO2已经呈现出较好的光催化性能. 同时, 光催化反应主要发生在催化剂表面,所以催化剂的表面结构对催化性能有很大的影响. Li等人[9]指出, 在TiO2晶格中掺入镧系金属离子可以起到电子捕获剂的作用，并降低半导体光催化剂的电子空穴对的复合率, 从而较好的提高了材料的光催化活性. 李聪等人[10]计算了La/Ce/Pr/Nd单掺杂TiO2体系, 计算结果显示这些体统的光学特性均得到有效改善. Saqib等人[11]研究发现, 利用稀土金属对TiO2进行表面改性后, 可以通过改变工作波长来减小带隙和抑制锐钛矿到金红石的相变, 从而提高了TiO2在可见光区的光催化效率. Liu等人[12]从理论上预测, Eu掺杂体系和N掺杂体系的带隙会变窄, Eu-N共掺杂体系显示出吸收边缘的显著红移, 增强了可见光光催化活性. Huang等人[13]利用DFT+U的方法研究了La和N共掺杂TiO2体系, 结果表明掺杂体系的带隙均出现了不同程度的减小, 致使所有掺杂体系在可见光区域的光催化强度均有不同程度的提高. Muhammad Nasir等人[14]利用溶胶-凝胶方法合成了Sc-C共掺TiO2体系, 钪掺杂浓度的增加使得电子和空穴的复合率增大. 共掺杂体系与单C掺杂样品相比, 较大的增强了酸性橙7的降解.光催化性能的增强主要归功于晶体尺寸的减小、表面面积和羟基基团的增加及电子空穴对寿命的增大. Song等人[15]尝试用两步法合成了稀土掺杂钛纳米棒(RE-TiO2NRs), 其作为光催化剂模拟了在太阳光照射下木质素的降解情况.使用甲基作为探测分子, 证明了Eu-TiO2NRs是降解MO的最佳方法之一. Er3+掺杂的TiO2NRs在降解MO方面显示出比商业上更高的光催化效率. Li等人[16]报道了采用微波干燥法和溶胶 - 凝胶法合成了Y和Ce共掺杂TiO2光催化剂. 结果表明该体系具有较高的光催化活性.

2计算方法和模型

本文利用vasp软件包和缀加平面波方法计算了掺杂模型的几何结构、能带、态密度和光学性质. 众所周知, 密度泛函理论通常低估含有d层和f层原子的带隙. 因此, 本文应用DFT+U方法处理了Ti原子和La原子d层电子之间强烈的库仑排斥作用, 有效的Hubbard参数(U-J)分别为5.3 eV和7.5 eV[5,17].利用GGA+U方法计算得出纯TiO2的带隙值为3.22 eV, 其与实验值(3.2 eV)很好的达成了一致[18].

图1表示TiO2(101)面的掺杂模型,模型包含72个原子或3个TiO2层，并且在Z轴方向上添加了15 Å的真空层.几何优化时最底层的TiO2层被固定, 以此用来模拟块体. 计算中, 使用PBE泛函的广义梯度近似方法描述了交换关联势,Ti原子、O原子和La原子的价电子分别采用3p63d24s2、2s22p4和5p66s25d1, 平面基组的截断能设置为500 eV, 几何优化和电子性质计算时的K点网格分别采用了2×2×4和3×3×6, 当每个离子的能量和力低于10-5eV和0.01 eV/Å时计算终止.

图 1 锐钛矿TiO2(101)面2×2×2超胞的平面图(a)和鸟瞰图(b). 红球、灰球和蓝球分别代表O原子、Ti原子和插入原子. La原子的掺杂位置分别为两种Ti原子、三种氧原子和两种插入原子.Fig. 1 The 2×2×2 supercell slab model (a) and a top view (b) for the anatase TiO2(101) surface. The red spheres, the grey spheres and blue spheres represent O, Ti and inserted atoms, respectively. The doped positions of La atom, as two kinds of Ti atoms, three kinds of oxygen atoms and two kinds of inserted atoms, are shown.

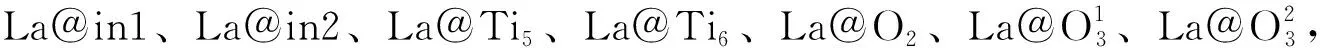
3结果和讨论

3.1形成能

掺杂体系的相对稳定性可以用形成能来进行判断, 形成能的公式如下：

Efor=Ed-Ep+m(μO-μLa)+n(μTi-μLa)-kμi

其中，Efor表示掺杂体系的形成能，Ed和Ep分别表示掺杂体系和未掺杂体系的总能量, m, n 和 k分别表示La原子置换O原子的数量、La原子置换Ti原子的数量和插入La原子的数量.μLa表示La原子的化学势，其可以通过La块体计算得出.μTi和μO表示Ti原子和O原子的化学势，它们可由Ti块体和氧气计算而来，并且它们之间满足2μO+μTi=μTiO2公式. 计算形成能时,μTi和μO的值与掺杂体系形成的环境密切相关. 当富Ti的环境下，μTi和μO的值分别为-7.68 eV和-9.47 eV; 当富O的环境下,μTi和μO的值分别为-18.34 eV和-4.14 eV. 本文计算的形成焓为-10.23 eV, 这与其他文献[22]报道的值(-9.6 ± 0.8 eV)较为一致.

表1 La单掺杂和双掺杂TiO2(101) 面的形成能和总能量

3.2几何结构

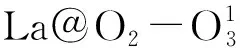
3.3电子结构

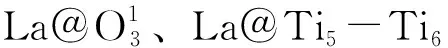
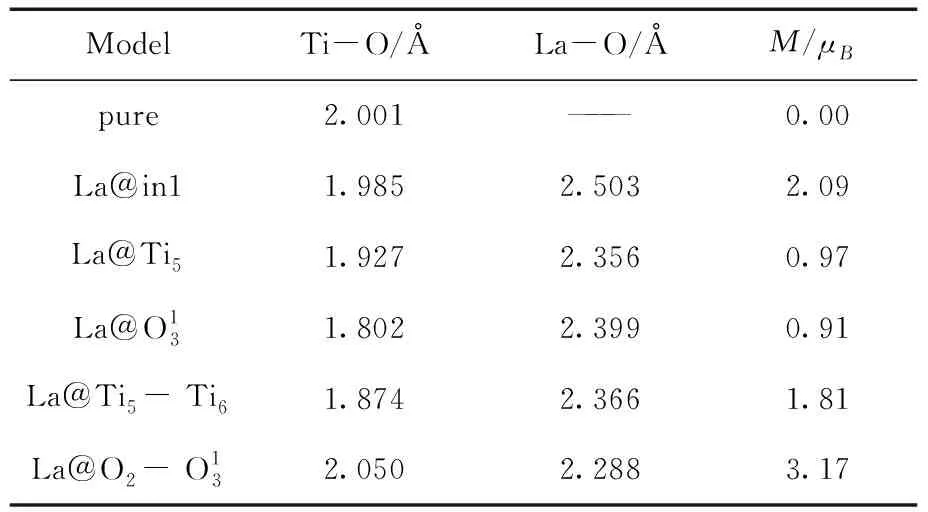
表2 几何结构优化后纯TiO2(101)面和掺杂模型的平均键长和总磁矩M

图2 未掺杂和掺杂TiO2 (101)面的能带结构、总态密度和分态密度虚线表示费米能级Fig. 2 The energy band structures, total density of states and partial density of states of (a) Pure (b)La@in1 (c) La@Ti5 (d) (e) La@Ti5- Ti6@G (f) Fermi energy is indicated by a dotted level.

表3 纯TiO2(101)面和掺杂模型的能带结构

表4 纯TiO2 (101)面和掺杂模型的bader分析

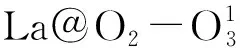
3.3光学性质

通过介电张量可以计算得出模型的吸收谱, 虚部和实部之和构成了介电常数, 公式如下：

ε(w)=ε1(w)+iε2(w)

(1)

其中,ε1(w)是实部,ε2(w)是虚部,w是光子的频率. 虚部可以通过计算空带之和得出, 公式如下：

(2)

介电张量的实部可以由Kramers-Kronig方程变换得出：

(3)

其中,p表示理论值.

在获得介电张量值后, 可以通过下式得出吸收系数α：

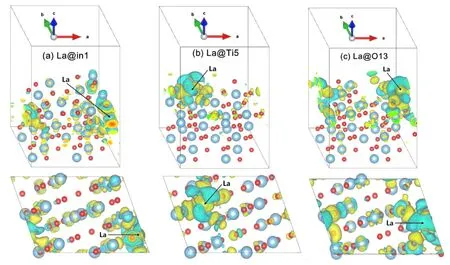
图3 纯TiO2 (101)面和掺杂模型的差分电荷密度Fig.3 Differential charge densities of pure TiO2 (101) surface and doped models

(4)

这些用于计算吸收系数的公式(1)-(4)源于文献[23].

图4 未掺杂和掺杂TiO2(101)面模型的吸收谱 Fig. 4 Absorption spectra ofpure and doped TiO2(101) surface models

4结 论

本文利用基于密度泛函理论的第一性原理方法研究了La未掺杂和单/双掺杂TiO2(101)面的电子结构和光学性质, 并讨论了其内部的微观机制. 研究结果表明：

(1) La掺杂TiO2(101)面时,可以引起晶格畸变和偶极矩的产生.