例谈“等”与“不等”的辩证转化

江苏省海安市实验中学 (226600) 刘国华

在现实世界中，等量关系和不等量关系是普遍存在的，它们既对立又统一，可以相互转化.在数学解题中相等与不等是矛盾的两个方面，在一定的条件下相等可以看着是不等的临界点，而不等是相等的进一步延伸和拓展，根据题目中的信息适时进行相等与不等的机智转化，可快速打开解题的通道或简化解题过程，本文剖析几个典型题目，供参考.

1.相等问题不等解

在一些题目中给出了等式条件，需要解决范围、值域等不等问题，这需要将已知等式向不等式转化，常用的转化手段是利用基本不等式和二次方程根的判别式.

例1 若正实数a、b满足ab=a+b+3，求ab与a+b的取值范围.

评析：本题是运用基本不等式转化解题典型例子，由a、b是正实数可联想到它是运用基本不等式先决条件，而后续的解不等式则是求范围的常规手段.

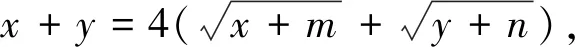
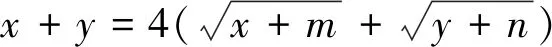
评析：本题是已知最大值求相关参数的值，从给出的等式条件中求出x+y的最大值是解题的关键，基本不等式的运用为问题的解决提供了重要保障.

例3 设x、y、z都是实数且满足条件x+y+z=0和xyz=2，求|x|+|y|+|z|的最小值.

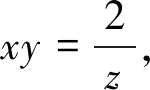
|x|+|y|+|z|的最小值为4.

评析：本题抓住所给的两个等式条件，利用二次方程根与系数的关系构造了一个一元二次方程，运用二次方程根的判别式得到了某个未知数的范围，顺利地将相等条件转化为不等关系.

例4 已知p、q都是实数且满足p3+q3=2，求p+q的最大值.

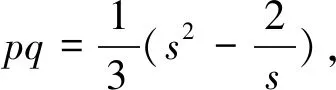
评析：通过设参数s，利用已知条件将p+q与pq同时由s来表示，为构造一元二次方程、运用根的判别式解题提供了先决条件.

2.不等问题相等解

在一些不等式题目中，如果考虑到函数、方程、不等式是三位一体的，就可以从函数图象的分析和方程根的讨论为突破口，从而使破题思路开阔、解题方法灵活.

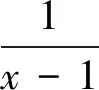
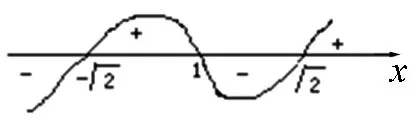
图1

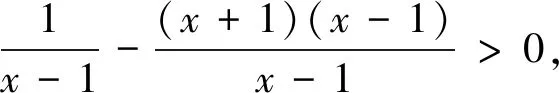
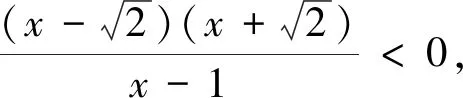
评析：本题是介绍了解高次不等式的一种方法，解题要点是：①将不等式一边变为0，另一边分解因式并整理成(x-x1)(x-x2)…(x-xn)的形式；②构造对应的方程，求出方程的根；③在数轴上标出各个根，并根据各个因式的符号画出各段的符号，最后得到不等式的解.

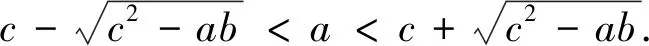
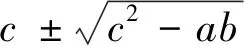
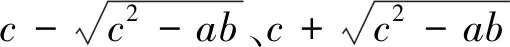
例7 已知|a|<1，|b|<1,，|c|<1，求证：ab+bc+ac+1>0.

解析：设x=a，则有一次函数f(x)=bx+bc+cx+1=(b+c)x+bc+1，∵|b|<1，|c|<1，|a|<1，即x∈(-1,1)，由于f(-1)=-b-c+bc+1=(1-b)(1-c)>0，f(1)=b+c+bc+1=(1+b)(1+c)>0，就是说一次函数f(x)=(b+c)x+bc+1在x∈(-1,1)的图象位于x轴上方，∴(b+c)a+bc+1>0，即ab+bc+ac+1>0.

评析：在题目中没有函数的影子，但通过设x=a(也可以设x=b或x=c)就将已知条件集中到一次函数问题中了，然后再对所给的范围进行分析，结合函数图象的位置就使问题获得了圆满的解决.

例8 若p∈R且|p|<2，不等式(log2x)2+plog2x+1>2log2x+p恒成立，求实数x的取值范围.

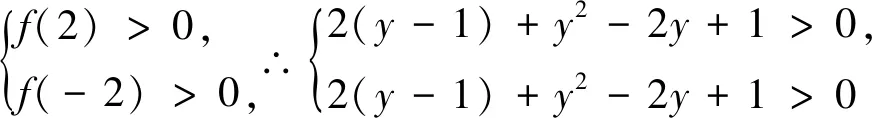
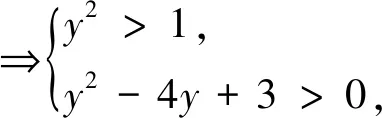
评析：本题运用变换主元的方法构造了一个一次函数，改变了原来问题的结构和设问方式，通过研究函数图象的走势得到不等式组，将原问题转化为解不等式(组)的形式.

以上举例介绍了解决不等式问题的变换方式，通过“等”与“不等”的及时转化，改变了问题的结构，把不熟悉的变为常见的，把复杂问题变为简单形式，为问题的破解或解题过程的简化创造了条件.