“数形”关联 “旧曲”新唱 深度学习能力自然生长
——以“二次函数图像与性质的复习”为例
2020-05-13江苏省太仓市第一中学215400朱建良
江苏省太仓市第一中学 (215400) 朱建良
“激发自主探究,提升学习能力”是变革初中数学课堂学习方式的主要途径,通过创设探索性数学问题情境,培养和发展学生的数学思维能力,以问题探究为载体,遵循数学学习规律,加深理解,揭示数学知识本质.笔者以“二次函数图像与性质的复习”为例,通过递进式的设问、变式拓展,以问题为思维导向,深入思考,意在帮助学生学会反思,感悟内涵,获得认知数学的方法.
1.一题多变——问题驱动探究
教师设计科学、合理的问题情境,拓展引申,辅助于学法指导,对原题的提问方式进行改变,对原题的结论进行延伸和扩展,也可把习题的因果关系倒置,以“一题多变”为载体,引导学生进行有效探究.帮助学生积累经验,通过问题驱动来引导学生不自觉地形成“分析问题能力”和“解决问题能力”.
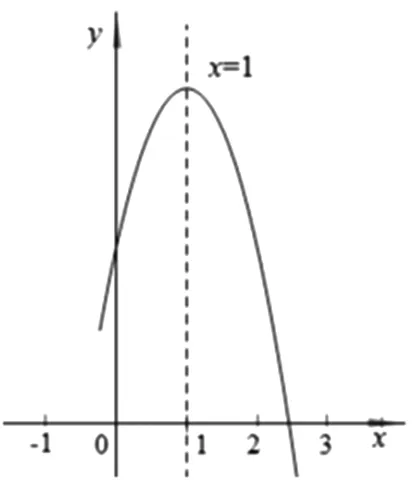
图1
问题1 如图1,已知二次函数y=ax2+bx+c(a≠0)图像的对称轴是直线x=1,其图像一部分如图所示.
(1)求证:2c<3b;
(2)若抛物线与x轴交于点(-1,0),问(1)的结论仍成立吗?
(3))若抛物线与x轴交于点(-1,0),与y轴的交点介于点(0,2)与点(0,3)之间,设顶点P(1,t),试求t的范围?
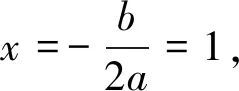
(2)当x=-1时,有y=a-b+c=0,有2c<3b.
设计意图:问题(1)(2)变化特殊点的坐标,揭示二次函数图像位置与系数a、b、c的数量关系之间的内在联系,加深学生对抛物线的轴对称性的理解.问题(3)把抛物线与y轴的交点问题转化为常数项c的变化区域讨论,再通过演算,推理出顶点P的纵坐标t的取值范围,问题设计流畅,环环相扣,较好地培养了学生的抽象意识和推理能力.
2.多题归一——挖掘问题本质
在“多题归一”探究中培养问题意识,在问题意识中实现自主探究,循序渐进,拓展开阔学生的数学思维,找到解决问题的通性通法,关注问题本质,把握内在规律,迁移解题方法,提高学习效率.
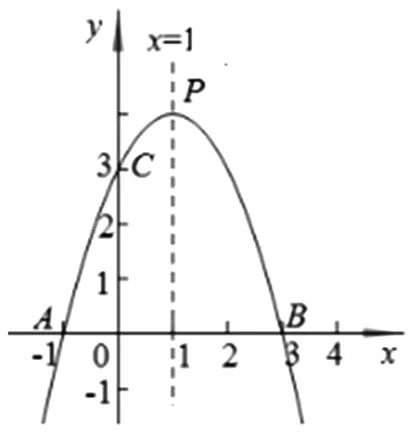
图2
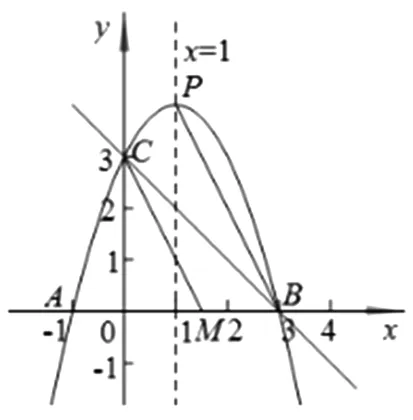
问题2 如图2,已知二次函数y=ax2+bx+c(a≠0)图像的对称轴是直线x=1,该抛物线与x轴交于A、B两点,与y轴交于点C,顶点为P,若已知点A(-1,0),OB=OC.若关于x的方程ax2+bx+c=m有实数根,求m的取值范围.
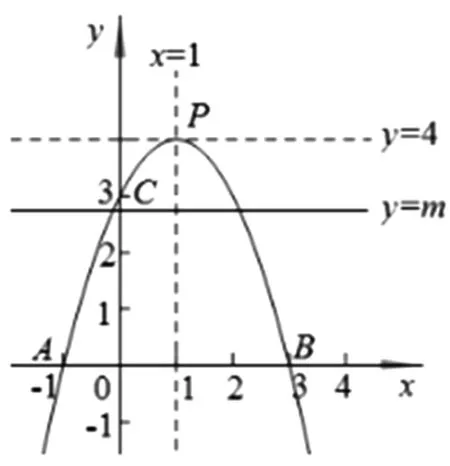
图3
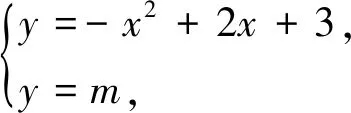
设计意图:问题2把讨论关于x的方程实数根的情况转化为直线与抛物线交点问题,由“数”联想到“形”,再由“形”的特征求解“数”的范围,涉及构造法,转化思想,方程思想,问题的求解巧妙地把画图操作、观察发现、探究计算融合在一起,较好地增强了学生的实践能力,培养了学生的创新精神.
变式1 若关于x的方程|ax2+bx+c|=k(k≠0)有四个不相等的实数根,求k的取值范围.
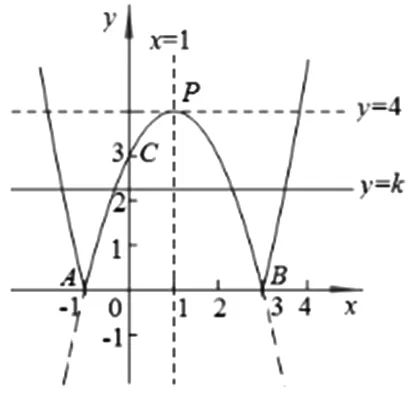
图4
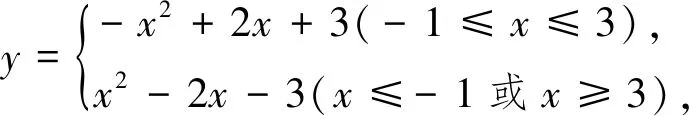
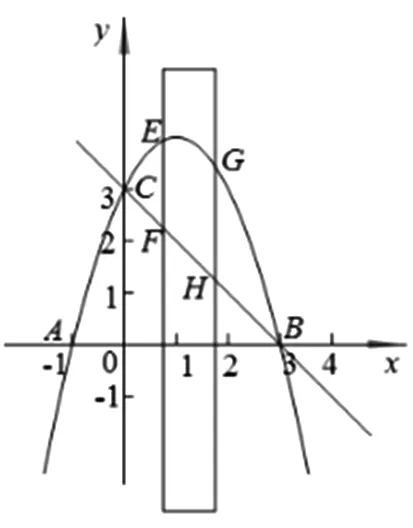
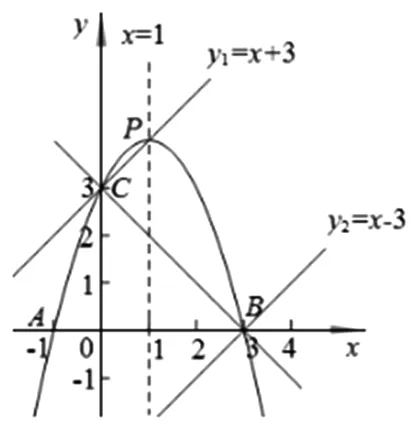
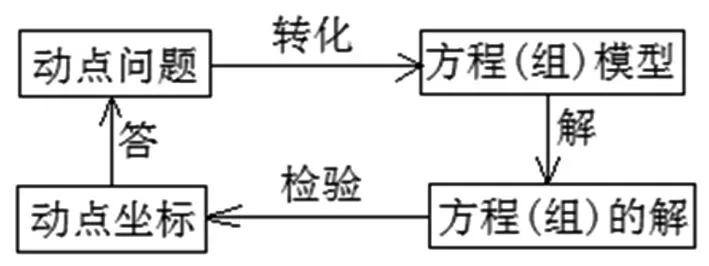
再分别讨论两支抛物线图象与直线y=k的交点情况,当0 变式2 若关于x的方程ax2+b|x|+c=n有两个不相等的实数根,求n的取值范围. 图5 设计意图:在原抛物线模型的条件下,变化自变量x的绝对值条件,分类讨论,根据对称性画出抛物线的另一半图像,问题显得“丰满”,由“数”及“形”,抛物线的对称轴由x轴到y轴变化位置,丰富了图形内涵,提升了思维层次.问题2的变式出的新问题合乎情理,合乎逻辑,数学思维训练变得精彩纷呈. 初中数学课堂教学设计关注数学知识系统性的整体架构,通过对问题解决过程的反思,典型问题进行“归类”,建立数学模型,通过建模找到解决问题关键点和突破口,并提炼出解决某类问题的方法,自动建构模型,有效迁移,达到“以题会类”的教学境界. 图6 拓展1 续问题2,如图6,能否在抛物线上的找一点Q,使ΔBCQ是以BC为直角边的直角三角形,试求出点Q的坐标. 解析:如图6,作垂直于直线BC的两条直线y1=x+3,y2=x-3,把直线与抛物线的交点问题转化为 设计意图:设计探求特殊动点坐标问题,引导学生整体认识图形特征,细心分析动点Q显性或隐性的不变元素,构造方程模型求解几何图形的特殊点坐标,归纳总结,提炼方法,通法不仅可以帮助学生理解动点坐标的本质,也可优化思维过程,形成自我方法优化,快速准确地解决问题. 变式3 能否在抛物线上的对称轴上找一点G,使ΔBCG为直角三角形,试求出点G的坐标. 剖析典型问题,寻找问题源,引导学生逐一回顾处理相关问题的知识源,分析知识源的典型特征,选取适当的问题源拓展延伸,帮助学生感悟“数学问题一般都是运用所学过的知识加以解决的”的转化思想,达成学习目标. 图7 变式4 如图7,续问题2,如图点M为x轴上的一点,若∠PBC=∠MCB,试求点M的坐标. 设计意图:变式问题的本质是抛物线背景下几何图形的特征探究,二次函数相关问题的特征是数形结合的有效载体,函数模型是客观世界的重要模型,变式问题中直线CM的构造与求解的解析式是解决问题的突破口,也是数形结合的有效衔接环节,其探究思路如下图示: 在提升学生应用知识和技能解决问题的能力的同时,渗透情感体验和价值观的建构,教会学生观察、分析、抽象和概括;归纳、演绎和类比进行推理,会准确地阐述自己的思想和观点;升华学生数学思维的宽度和深度,形成良好的数学思维品质. 图8 拓展2 续问题2,如图8,宽度为1的直尺平行于y轴,在点B、C之间平行移动,直尺的长边所在直线被直线BC和抛物线截得两线段EF、GH,设F点横坐标为m(0 解析:F(m,m+3),则E(m,-m2+2m+3),可计算出EF=-m2+3m,同理得GH=-m2+m+2,EF-GH=2(m-1),∴当0 设计意图:由动点位置变化拓展到特殊线段长度的比较,透视现象看本质,类比探究,把线段长转化为动点坐标表示,由问题导学,将学生的思维引向解决问题的方向,关注学生了的持续生长,使学生经历的不仅是一个解答,更是一种研究问题的方法. 以变式拓展的问题串为探求线索,引导学生身历问题情境,获得体验,积累经验,通过动点、动直线与抛物线位置关系的变化为载体,问题设计强化了抛物线的对称性,强调用图意识,变式拓展问题呈现了学生数学思维的碰撞,动态问题的探究引导学生感悟本质,获得思维深刻性,使数形结合成为自觉,从而提升学生逻辑推理、直观想象、数学运算等核心素养.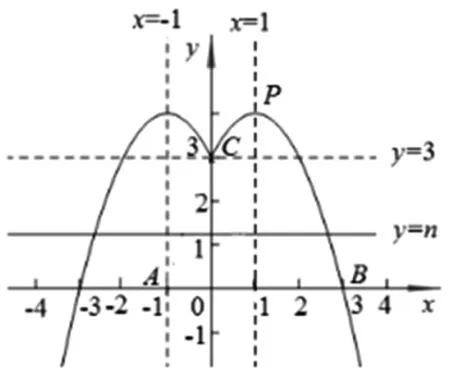
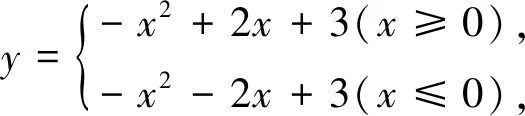
3.强化模型——寻找问题突破口
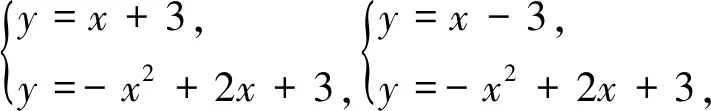
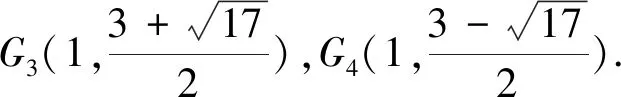
4.“生长”问题——唤醒问题生命力
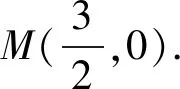
5.能力立意——提升数学素养