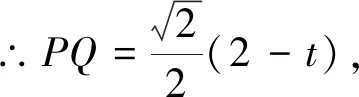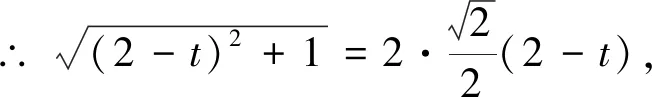例析立几中的探索性问题

江苏省金湖中学 (211600) 王 锋

立体几何的探索问题在近几年高考中常常出现，这种题型有利于考查学生推理、探索、判断等各方面能力，也有利于创新意识的培养，所以应该注意对这种新题型的研究，下面举例谈谈常用的求解策略.

一、直接探求

在分析研究所给问题后，尝试给出欲求的条件，再进行证明.

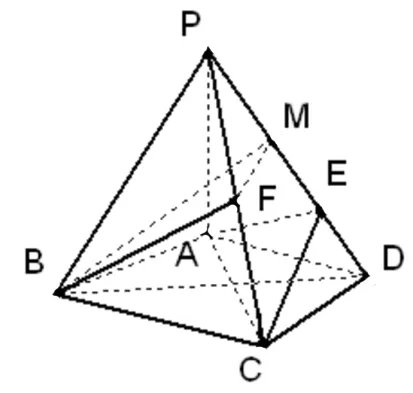
图1

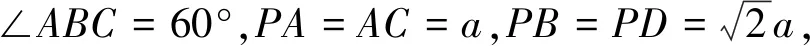
(1)证明：PA⊥平面ABCD;

(2)求以AC为棱，EAC与DAC为面的二面角θ的大小;

(3)在棱PC上是否存在一点F，使BF∥平面AEC?证明你的结论.

解析：(1)(2)略.(3)猜测F是PC的中点时，有BF∥平面AEC.

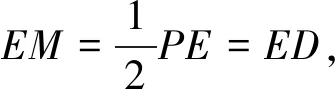
二、假定求解

对某些是否存在型的问题，可先假定存在，再探索存在的条件，并证明是否合理.

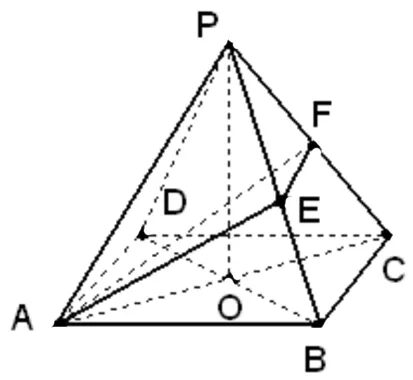
图2

例2 如图2，正四棱锥P-ABCD中，AB=2，侧棱PA与底面ABCD所成角为60°，问在线段PB上是否存在一点E，使AE⊥PC，若存在，试确定E的位置，并加以证明；若不存在，请说明理由.

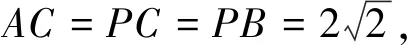
三、化归代数

通过解三角形建立函数关系或方程，利用代数知识判断存在性.

图3

例4 如图3，在四面体ABCD中，AB⊥BC，AB⊥BD，BC⊥CD且AB=BC=1，问是否存在这样的四面体，使二面角C-AD-B的大小为30°，如果存在，求出CD的长；如果不存在，请找一个角θ，使得存在这样的四面体，使二面角C-AD-B的平面角为θ.

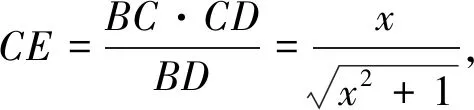
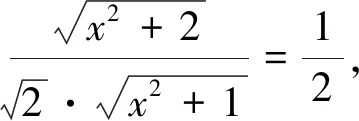
四、引入参数

对需确定点的位置的问题，可利用参数列式求解.

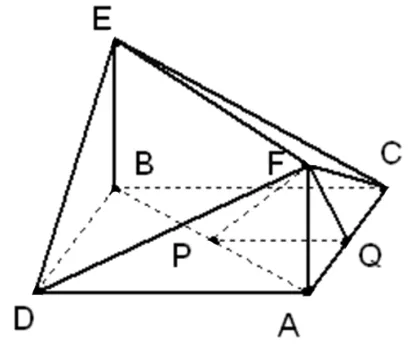
图4