刍议高效微专题复习应注意的几个方面*

湖南省长沙市明德中学 (410009) 杨 果

*基金项目：本文是湖南省教育科学研究工作者协会2018年度重点课题“新高考背景下中学课堂教学培养学生数学核心素养的策略研究”(课题编号：XJKX18A006)阶段性研究成果.

高三综合复习的知识量很大，单纯按照章节顺序复习知识点，反复做大量题目，大搞题海战术的方式早已为人诟病，且这样的课堂一般略显沉闷，学生身心疲惫，教师负担繁重，课堂效率低下.如何改变这种局面？文[1]以“专题引领，提升素养，打造数学复习课新常态”为题研讨了在传统复习模式中穿插微专题复习的重要性，但笔者思考微专题复习的效率还有没有进一步提高的方法？学生主动参与的积极性还有没有进一步提升的空间？

教育部考试中心主任姜钢曾在《中国教育报》发表署名文章《牢记立德树人使命，写好教育考试奋进之笔》，文中指出今后的新高考要着力凸显核心素养，全面提升选拔效能，大力推进素质教育，这就决定了我们的高三复习不能穿新鞋走老路，而应在高三复习时仍注重培养学生的核心素养，减负和高效我们都需要.

笔者下面以微专题“圆锥曲线的定点问题”为例，谈一谈关于高效微专题复习应注意的几个方面，以期抛砖引玉，与广大同行深入探讨.

一、选题方面——要注重代表性

波利亚认为一个精心备课的教师应该拿出一个不太复杂却十分具有代表意义的题目，使学生通过这道题目就好比通过一道门，去发掘知识的各个方面.

笔者认为微专题复习的选题是首要应该考虑的方面，不见得是越难的题目越好，不见得是面面俱到的题目就适合，而应该选择那些起点低，入口广，代表性强，且易于变式的例题，比如下面这道.

例题已知抛物线方程为y2=4x，过抛物线的顶点O作两条互相垂直的弦OA、OB，试问：直线AB是否恒过一个定点，若是，求出定点坐标；若不是，说明理由.

评析：该题作为圆锥曲线的定点问题中的例题，让人感觉十分亲切，题干简洁，条件叙述干净利落，问题指引清楚明晰，曲线方程和两直线的垂直关系都具代表性，并且作为一个开放型问题，有利于学生发散思维，有利于教师引领变式.

二、解题方法方面——要注重通性通法

微专题复习不要片面追求“一题多解”，不要过于追求难以想到的技巧，如果过于追求一题多解，遍地开花，则会冲淡主题，学生的主体地位会被教师的个人秀取代，而那些犹如神来之笔的技巧，既不容易为学生所理解，也不容易为学生所掌握.笔者认为一般最多讲透三种主要的通性通法即可，解题技巧则要贴近学生的最近发展区.

法1：用解交点的方法(从直线OA切入)

综上，直线AB恒过定点(4,0).

法2：代点法(设点消元)从A，B的坐标切入

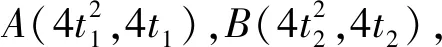
综上，直线AB恒过定点(4,0).

法3：联立方程组用韦达定理(从直线AB的方程切入)

当直线AB不与x轴垂直时，设AB:y=kx+m(k≠0)，A(x1,y1),B(x2,y2)，

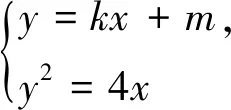
综上，直线AB恒过定点(4,0).

三、问题探究方面——注重变式训练，培养逆向思维，举一能反三

变式已知抛物线方程为y2=4x，过O作两条弦OA、OB，欲使直线AB恒过x轴上的定点(t,0)(t≠0)，则A，B两点应满足什么样的条件？

探究1从A，B两点的坐标探究.因为直线AB恒过x轴上的定点(t,0)，故而可以将直线方程设为x=my+t，再与y2=4x联立消去x得y2-4my-4t=0，利用韦达定理得到y1y2=-4t为定值即可.

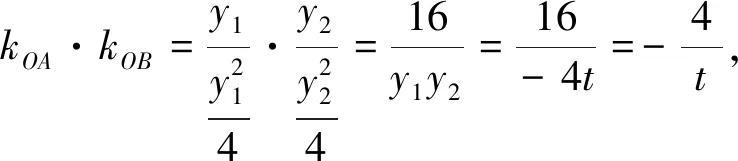
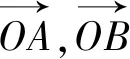
评析：该变式是将结论与条件翻转，仍是开放性探究，且开放性更大，而探究的三个方面——坐标关系、斜率关系、向量关系都是常见类型，学生喜闻乐见.

四、结论拓展方面——紧扣最近发展区，注重可推广性

五、结语

前面的案例只是一个微专题复习的缩影，我们在高三复习时还可以发挥得更多更多，比如对于椭圆、双曲线、圆是否有类似结论和相应探究？甚至其它章节的知识点，是否也可以从选题、解题、探究、拓展几个应注意的方面来设计？这都值得我们去认真探索.

总之，新高考已经到来，据说将来数学高考还有可能出现多选题和更加开放型的探究题，这就需要我们更加注重提高包括微专题在内的高三复习课的效率，更加注重培养学生的核心素养，强化学生在课堂的主体地位.