着眼局部 把握整体 理解本质 完善认知*——分段函数奇偶性判断的深度理解与教学感悟

安徽省阜阳市红旗中学 (239000) 潘 静

案例设函数f(x)是定义在R上的奇函数，若当x∈(0,+∞)时，f(x)=lgx，则f(x)在R上的解析式为.

分析：因为函数f(x)是定义在R上的奇函数，故f(0)=0，因此只要再求出x>0时f(x)的解析式即可，当然此种情况求解并不难，通常解答如下：设x<0则-x>0，因x∈(0，+∞)时，f(x)=lgx，所以f(-x)=lg(-x)(※)，又函数f(x)是定义在R上的奇函数，故由(※)得，-f(x)=lg(-x)，即f(x)=-lg(-x).

一、问题提出

上面的解答方法通常称为“转代法”，此法自然流畅，易于掌握，是处理这类问题的通法，无论高一新课教学，还是高三备考教学中，如果遇到上述类型的试题，就常常使用这种方法，可以说是我们教师的拿手好戏，教学起来得心应手，顺风顺水，没有什么悬念.然而笔者最近在高三备考教学中，在展示上述解法之后，出现了意外，一位学生提出质疑：“老师，在等式(※)中，对应关系f不是‘取常用对数lg口’吗？那为何根据‘f(x)是定义在R上的奇函数’，可以将f(-x)变换为-f(x)，而lg(-x)却不能将‘-’移出来写成-lgx呢？”一石激起千层浪，对呀，这位同学说得好，大家看，为何在等式f(-x)=lg(-x)中，左边f(-x)的负号“-”可以移出来，而右边式子lg(-x)中却没有将负号“-”移出来？不少学生说，因为此时x<0，lg(-x)中不能将负号“-”移出来，否则-lgx无意义，的确如此，但这种分析能否作为“(※)中lg(-x)中不能将负号“-”移出来”的理由呢？显然，有些牵强附会，不能说服一部分学生，于是又大家面面相觑，看起来不少学生仍在陷入沉思之中，既然(※)中对应关系f是‘取常用对数lg口，等号右边不可将“-”移出来，到底怎么回事呢？

二、问题解决

因为上述案例中的函数f(x)是分段函数且是奇函数，故f(-x)=-f(x)中等号两边的对应关系f是不同的,故设x<0，则-x>0，因x∈(0,+∞)时，f(x)=lgx(“f”此时是指“取常用对数lg口”)，所以f(-x)=lg(-x)①(“f”此时是仍指“取常用对数lg口”).又f(-x)=-f(x)②(注：此变换悄悄地使得对应关系“f”的意义发生变化)，故由、通过等量代换，得到的-f(x)=lg(-x)中的“f”已不是“取常用对数lg口”，而是-lg(-口).

而在f(-x)=lg(-x)(x<0)中，“f”的意义就是“取常用对数lg口”，为何等号左边的负号“-”能移出来，而等号右边的式子lg(-x)中负号“-”不能移出来呢？

为了方便解释，对于本案例中对应关系，不妨设当x>0时，对应关系f记为“f1”，当x<0时，对应关系f记为“f2”(注：f1与f2一定不同)，则由上面的分析知，当x<0时，有f1(-x)=lg(-x)，又根据f(x)是奇函数，我们可以得到当x<0时，使得

f1(-x)=-f2(x)，即得 ，而对于对数函数 不是奇函数，故没有这种功能，即没有lg口.虽然在lg口中，“lg口”的意义就是“取常用对数lg口，我们根据f(x)是奇函数，将-中的“-”号移出，但对应关系由“f1”变为“f1”了，而不是原来的对应关系了，由于f1与f2统一地记为f，故只能由f(-x)=lg(-x)(x<0)得到-f(x)=lg(-x)，而不能将lg(-x)中的“-”号移出.

因此当分段函数又是奇函数(或偶)时，我们不能用固有的眼光去看待分段函数对应关系“f”，要从整体上去认识对应关系“f”，切不可将分段函数f(x)的对应关系“f”与构成分段函数每段的函数对应关系混为一谈，否则，本案例中的质疑就难以得到诠释.

三、教学思考

此案例中学生提出的质疑的确困扰着一部分善于思考的学生，由于我们不少教师平时没有对此问题作进一步的深入思考，当学生向教师提出上述质疑时，就用“若将f(-x)=lg(-x)(x<0)中

lg(-x)的‘-’移出，则lgx就无意义”去搪塞学生，结果学生还是不明白，知其然不知其所以然，这种教学现象充分说明我们有些教师在解题教学时只是为解题而解题，没有将解法形成的原因即算理讲清楚，导致学生只会照猫画虎，机械地模仿操作，缺少思维活动的展示，这就严重违背了与“数学教学是思维活动的教学”，到头来，学生不能学到真正的数学，得到的只是一个个被动接受的数学知识方法而已.

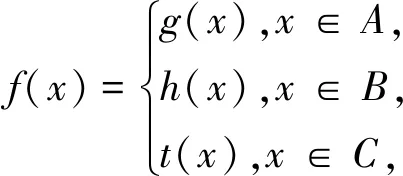
当然，讲清楚有时是不容易的，这就要求教师平时多思、多悟，将数学教出活力，教出数学味.笔者在教学中不甘平庸，时常对大家熟视无睹的数学现象都会深思一番，收获颇丰，教学起来就能驾轻就熟，深入浅出，学生听得明白，易接受.然而，很多教师在当今的教学中受急功近利的影响，只知道展示解题过程，至于为什么这样处理，而不那样处理，却解释得少，思考得更少，上述案例得质疑看似简单，实则不易，如果教师不静下心来潜心研究一番，还真找不出症结所在，试想：因为教师如果讲得不透，学生的负担不是越来越重吗？因此要使学生学得轻松，教师教学时必须讲得清清楚楚，通俗易懂，让学生学得更明白一些，不知其理，反而学得更辛苦.难怪很多高一学生感到高一数学学得吃力，是情理之中的事，因为我们教师在教学中对于抽象的数学知识及思想方法未讲透彻，往往局限于“知其然，而不知所以然”的层面，讲解缺少深度，从而导致学生囫囵吞枣的多，试想：不理解的数学知识与方法，怎能谈得上灵活运用？