例析利用解平面向量题

福建省福安市第一中学 (355000) 徐志刚

一、化简配凑

点评：围绕判断△ABC的形状这个目标，将已知的向量条件向三角形的边角关系转化是成功解题的关键所在.

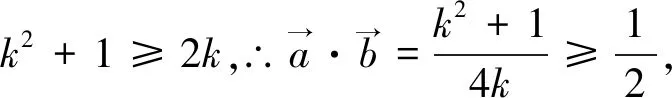
二、移项平方

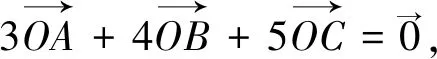
点评：本题中抓住O是△ABC的外接圆的圆心的性质，用平方的手段将向量问题转化为边长的关系，找到了隐藏的特殊角.

点评：本题中，利用换元的手段整体地解决了问题，这需要高瞻远瞩，有一定的知识储备，才能把握问题的实质.

三、分解向量

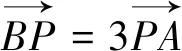
点评：通过对所给的条件和欲求的结论进行细致分析，将要求的向量问题分解，向已知的向量条件接近是解决问题的关键.

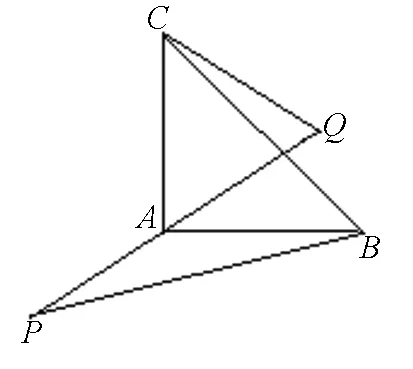
图1

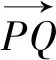
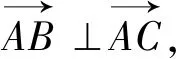
点评：抓住两向量的夹角，利用向量的线性运算，将数量积转化为代数形式，是转化向量问题的基本方法之一.

四、择机处理

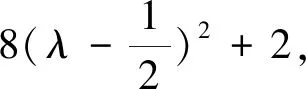
点评：向量中模的问题，平方是解决问题的主要手段之一，本题中通过平方化去了向量，使问题转化为较为熟悉的二次函数求最值问题.

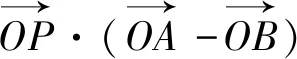
图2

点评：解题中抓住垂直平分线的“垂直”、“平分”的几何性质，通过有目的地拆分向量，使向量的数量积及时转化为已知的模的问题，目标明确，思路简洁.