缺失数据下滑动平均模型的估计方法

陈博, 何幼桦

(上海大学理学院, 上海200444)

在对时间序列数据预处理的过程中,数据存在缺失值的情况屡见不鲜.这种情况的发生不仅会造成预处理时间的增加,还将严重影响数据质量.此外,不同缺失数据的处理方法也会导致估计结果产生很大差异[1-2].因此,研究如何有效地处理缺失数据显得十分必要.

对于含有缺失数据的时间序列的处理方法,大致可分为两大类.第一类为借补法,即使用某种规则或方法来填补缺失数据,如取平均值、线性插值法等.该方法易于实施,但没有充分利用数据中一些关联信息且不依赖于模型结构.基于此,将缺失数据与模型相结合的第二类方法[3]被提出.

庞新生[4]介绍了多重插补法的基础理论与处理缺失数据时的基本思想.Junger等[5]将多重插补法应用于空气污染的时间序列中,并在缺失数据小于5%的情况下,取得了令人满意的结果.Machado等[6]简述了存在数据缺失时自回归模型的参数估计问题.Penzer等[7]运用Kalman递归估计方法完成了对缺失数据下ARMA模型的似然方程拟合.仝倩等[8]通过经验似然方法研究了含有缺失数据的半参数非线性模型的统计诊断问题.

除此之外,基于极大似然估计基础上的EM算法[9]也是一种重要的处理缺失数据的统计方法.该算法通过期望(E)步来得到一个平均意义下的似然函数,再通过最大化(M)步求得该次迭代似然函数的参数解,依此反复迭代得到最终的最优估计.Shumway等[10]为EM算法在时间序列上的应用打下了基础.田萍等[11-12]应用EM算法,针对含一个或连续两个缺失数据的AR(p)模型给出了具体计算步骤,并针对含1～2个缺失数据的ARMA(1,1)模型做出了参数估计,给出了其解析表达式.黄翔等[13]针对AR(p)模型的非左端缺失问题,且在缺失数据量较大时,通过EM算法提出了有效的缺失值插补方案.

本工作针对存在连续缺失值的MA(q)模型,综合了EM算法、极大似然原理及滑动平均(moving average,MA)模型的相关理论,得到了模型参数的合理估计,并在此基础上进一步完成了对缺失数据的填补.通过数值模拟,研究了估计的有效性和精度,并将该算法应用于实际数据,得到了较好的估计结果.

1 模型参数估计

对于样本序列X=(x1,x2,···,xn)′,满足q阶滑动平均模型MA(q):

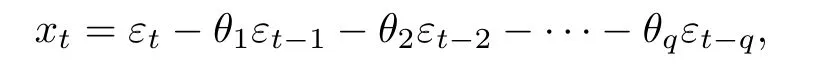
n≫q,{εt}iid～N(0,σ2),可得到方程组

记

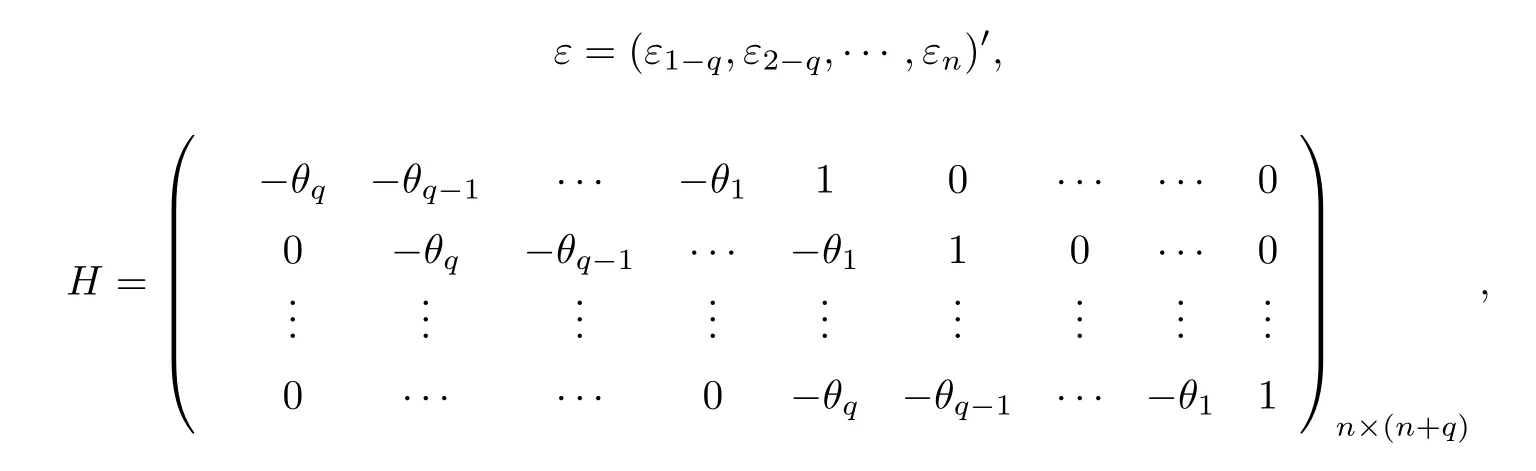
则原方程组可写为

未知参数φ=(θ1,θ2,···,θq,σ2)的似然函数为

若样本序列X中的(xs+1,xs+2,···,xs+r)为缺失数据,记为

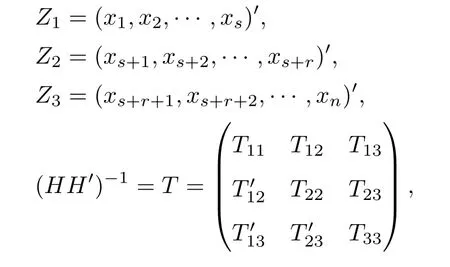
式中,T11,T22,T33分别为s,r和n-s-r阶方阵,对数似然函数l为

估计参数φ的EM算法步骤如下.

(1)E步.在获得第i步参数估计φ=φ(i)的条件下,对式(1)求关于Z2的条件期望:

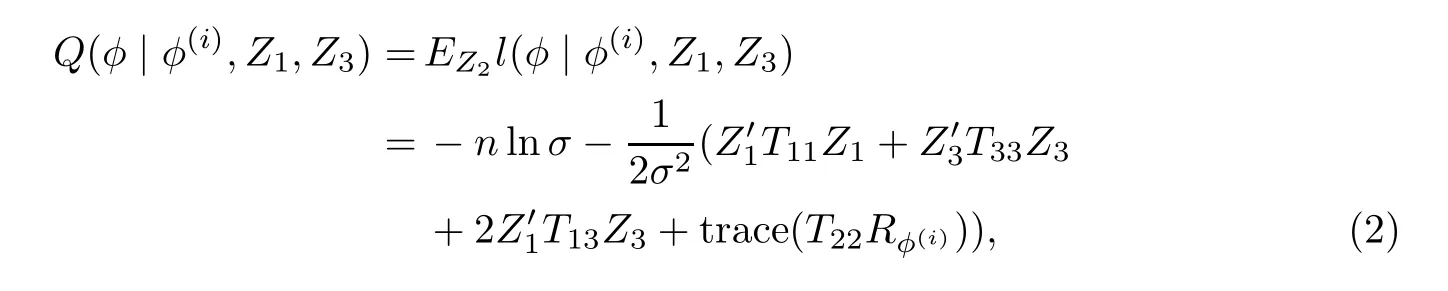
式中,Rφ(i)=E(Z2Z′2)为缺失数据Z2的协方差矩阵.

(2)M步.极大化式(2),即第i+1步参数估计为

在给定参数φ的初始值φ(0)后,便可通过EM算法重复迭代,直至||φ(i+1)-φ(i)||小于给定精度τ,以此保证迭代的收敛性[9].

2 缺失数据估计

在给定参数φ下,缺失数据Z2的估计Z2有如下结论.

定理1 若含有缺失值的序列X为滑动平均模型MA(q)的一组样本,则在二次损失下缺失数据Z2的估计为

证明 考虑如下约束优化问题:

该问题的拉格朗日乘子法目标函数可写为

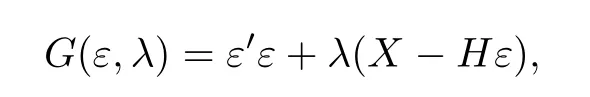
式中,λ=(λ1,λ2,···,λn)′.计算

代入约束条件,可得

得到ε的最优点为

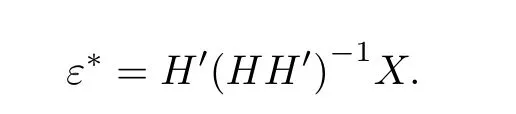
最后极小化ε∗′ε∗,可得

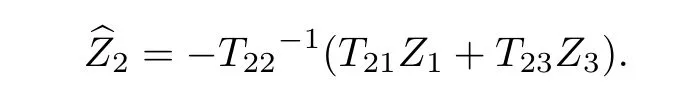
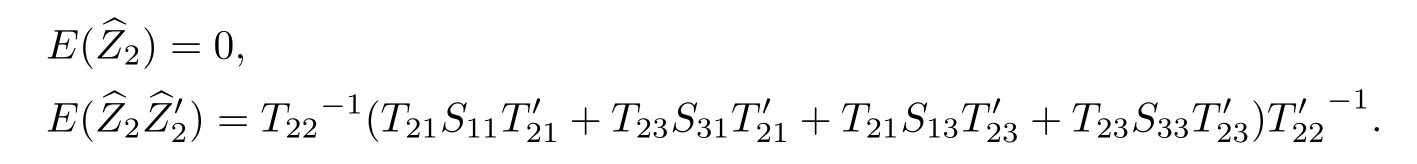
式中,S11,S31,S13,S33分别为s×s,(n-s-r)×s,s×(n-s-r)和(n-s-r)×(n-s-r)阶矩阵,则Z2的协方差矩阵为

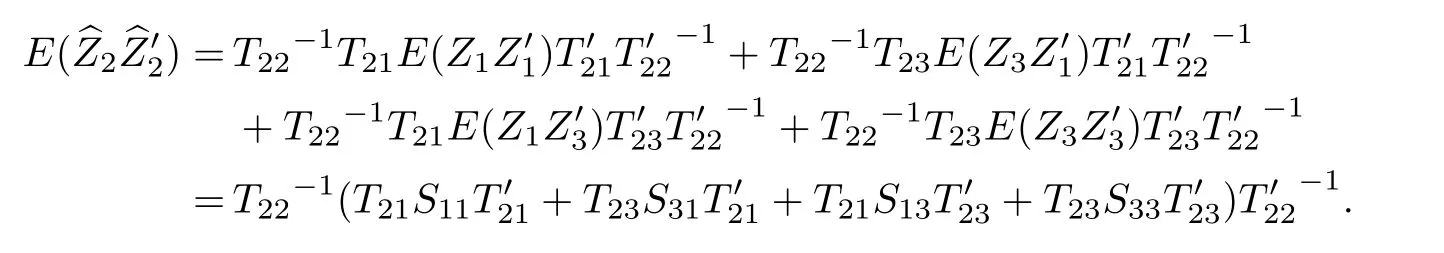
推论1 当缺失值在序列尾端,即s+r=n,则

证明 当s+r=n时,

因T与S/σ2互逆,由文献[14]得

代入式(3),可得

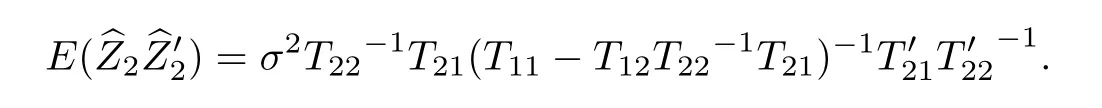
推论2 当缺失值在序列首端,即s=0,则

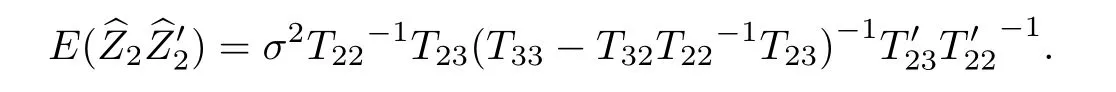
证明 同推论1.

而当缺失值在非序列首尾部时,类似地亦可完全用Tij直接表示出E(Z2Z′2),只是形式过于复杂,在此不再赘述.

3 数值模拟

设定序列长度为50,σ=1,缺失位置在序列中部,参数初始值设置为θ(0)=0,EM算法精度τ=0.000 1,以均方误差(mean square error,MSE)为评判标准.本工作将通过数值模拟比较在相同情况下本算法与文献[12]算法的参数估计效果,结果如表1所示.

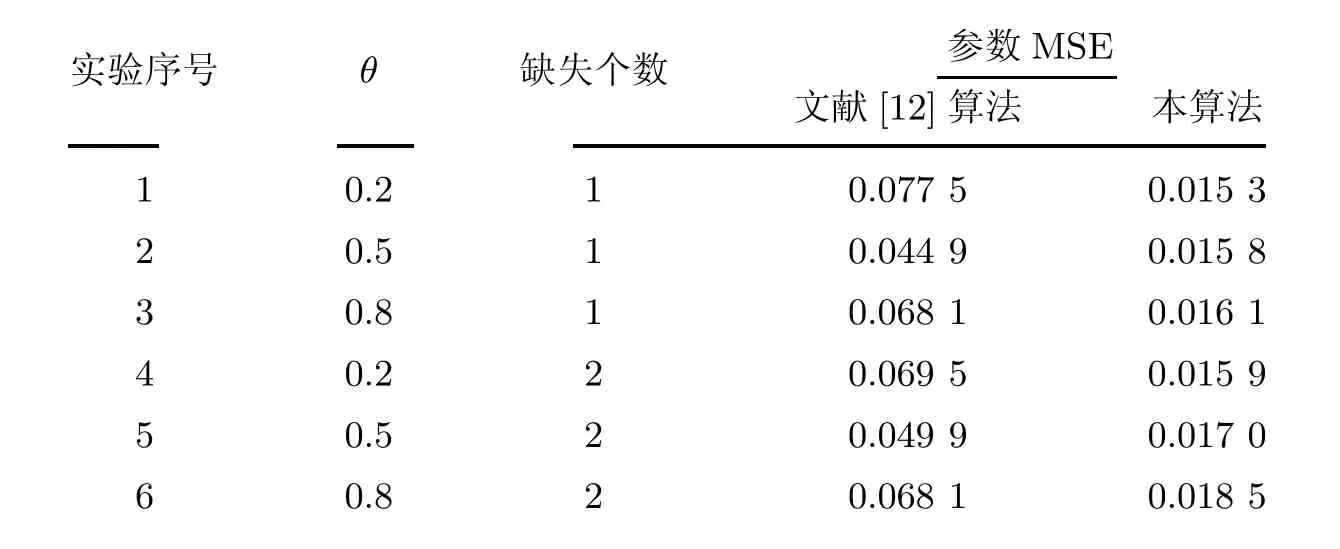
表1 算法误差对比Table 1 Algorithm error comparisons

由表1可知,本算法的精度明显高于文献[12],且文献[12]算法只能解决单个或连续两个数据缺失问题,也无法判断MA系数的正负性,而本算法则没有这些限制.

进一步地,本工作将通过数值模拟研究样本缺失比例、模型阶数、序列长度及模型特征根模长等因素对参数估计整体均方误差(MSEP)和缺失值估计整体均方差(MSEE)所造成的影响.记

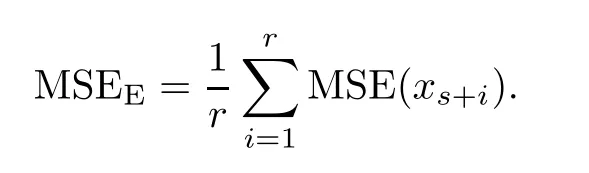
3.1 模型特征根模长、模型阶数对整体均方误差的影响

取序列长度为50,样本缺失比例为10%,观察在相同序列长度、样本缺失比例情况下,模型特征根模长与模型阶数对估计整体均方误差的影响,结果如表2,3所示.

表2 模型特征根模长、模型阶数与MSE P的关系Table 2 Relationships between length of model characteristic roots,order and MSE P

表3 模型特征根模长、模型阶数与MSE E的关系Table 3 Relationships between length of model characteristic roots,order and MSE E

由表2,3可得:当序列长度、模型特征根模长、样本缺失比例相同时,MSEP与MSEE均与模型阶数正相关,即二者随着模型阶数的增加而增加;当序列长度、模型阶数、样本缺失比例相同时,MSEP与MSEE同样均与模型特征根模长正相关,即二者随着模型特征根模长的增加而增加.模型特征根模长的大小反映了模型的平稳程度.数值模拟结果显示,模型越平稳,估计效果就越好.

3.2 序列长度、样本缺失比例对整体均方误差的影响

设定模型为模型特征根模长为0.1的MA模型,观察在相同模型阶数、模型特征根模长的情况下,序列长度与样本缺失比例对估计整体均方误差的影响,结果如表4,5所示.

表4 3阶模型中序列长度、样本缺失比例与MSE P的关系Table 4 Relationships between length of sequence,proportion of missing data and MSE P in MA(3)

表5 3阶模型中序列长度、样本缺失比例与MSE E的关系Table 5 Relationships between length of sequence,proportions of missing data and MSE E in MA(3)

本工作对不同模型阶数、不同序列长度和不同样本缺失比例的情况进行了数值模拟(表4,5仅为MA(3)的模拟结果).结果显示:当序列长度、模型特征根模长和模型阶数保持固定时,MSEP与样本缺失比例正相关,即MSEP随着样本缺失比例的增加而增加;当模型特征根模长、模型阶数和样本缺失比例相同时,MSEP与序列长度负相关,即MSEP随着的序列长度的增加而减少.序列长度及样本缺失比例对MSEP均有明显影响,MSEE但对此并不敏感.

4 实例计算

对2015年4月—2015年8月(共90日)的浦发银行股票日对数收益率数据进行建模,通过观察序列的自相关函数图可得序列的自相关函数是2阶的.因此,在MA(2)模型的假设下,其参数的最大似然估计为θ1=-0.026 1,θ2=0.299 8,σ2=0.000 8,并在5%的显著性水平下,接受该模型是二阶滑动平均模型的假设.

假设因某种原因,序列中的10%数据缺失,缺失数据起始位置位于2015年6月3日,连续缺失9日数据.通过本算法,在精度τ=0.000 1下,经过10步迭代得到模型的参数估计值为θ1=-0.018 3,θ2=0.294 1,σ2=0.000 9,与完整数据下的结果基本相同.记缺失数据估计Z=(z1,z2,···,z9),缺失数据估计的方差Var(Z)=(0.000 078,0.000 077,0,0,0,0,0,0.000 077,0.000 078),相关系数矩阵为

计算结果表明,在缺失数据下的模型参数估计与完整数据的结果之间仅存在很小的误差,证明本算法对参数估计是十分有效的.但是缺失数据估计的标准差与序列状态近似处于同一数量级上,说明缺失数据估计效果不如参数估计.由于当MA(q)模型的预测点与样本之间的距离大于q时,其最佳线性预报值为模型的均值,因此实例中缺失数据估计的方差在与样本距离大于2时均为0.同理,对于缺失数据估计的相关系数矩阵而言,当缺失数据与左侧样本之间的距离小于等于q时,则该类缺失数据估计之间存在着相关关系,而与其他缺失数据估计不相关.类似地,当缺失数据与右侧样本之间的距离小于等于q时亦是如此.