改进型任意风格快速迁移元网络算法*

刘运鑫，江爱文，叶继华，王明文

江西师范大学 计算机信息工程学院，南昌 330022

1 引言

图像风格迁移是图像纹理迁移的扩展，可以理解为提取风格图中的风格（纹理、颜色等），并与内容图相结合，进行图像重建，生成风格化的结果图。由于技术的局限性，传统技术只能做到纹理迁移，但随着卷积神经网络的发展，Gatys 等人[1]开辟了基于深度学习的风格迁移研究领域。他们的实验结果表明，图片的风格和内容可以被深度卷积神经网络分离并提取，通过不同内容和风格的融合，达到图像风格迁移的目的。他们提出利用Gram 矩阵作为风格统计量和损失，并证明相同风格的图片Gram 矩阵是相同的。他们的方法可以对任意尺寸的图像实现风格迁移并且能够生成相对高质量的风格化图片。但是，他们的方法优化过程十分缓慢，需要使用数百次的梯度下降过程来逼近最优的图像解，无法做到实时性。一旦更换目标迁移的风格，模型就需要重新训练。因此，Gatys 等人[1]的方法是典型的单模型单风格的风格迁移算法。

除了Gram 矩阵作为损失函数，Li 和Wand[2]提出了基于马尔科夫随机场（Markov random field，MRF）的非参数风格迁移的算法。该算法核心是使用MRF损失来代替Gram 损失，文献[3-5]都是此类非参数方法。除此以外，Li 等人[6]提出的均值和方差，Risser 等人[7]提出的直方图损失，Peng 等人[8]提出的CORAL 损失均可以作为风格损失来满足风格迁移的要求。

Johnson 等人[9]改进了Gatys 等人[10]的方法，使用前馈网络和感知损失进行风格迁移，大大提升了风格迁移的速度，在一定程度上做到了实时性。但是，此方法依然保留着对每一个新的风格都需要重新训练一个新的模型的局限性。

随后出现了大量风格迁移的算法，如文献[11-13]中的单模型多风格。他们能够做到单一模型实现多个风格迁移的效果。尽管如此，这些模型能够迁移的风格依然有限和固定。

本文关注的是更具挑战性和实际应用价值的单模型任意风格迁移[14-16]。

Fig.1 Method results of Ref.[17]图1 文献[17]方法结果

Shen 等人[17]提出基于元网络的任意风格迁移算法，成功实现了快速的任意风格迁移，并且拥有良好的实验结果，得到业界的广泛关注。经过反复实验作者提供的源代码，并仔细验证Shen 等人[17]的方法，发现该算法在进行风格迁移时，主要存在两方面的缺陷：（1）风格化后结果图片总是出现明显风格不一致的不协调像素缺块，如图1 所示。从图1 中可以看出几乎每一张图片都有一个比较明显的灰色椭圆形缺块（在图中已用红框标出）。在该算法中，这是一个普遍现象。（2）图1 中风格图与风格化后的结果图，在颜色布局上通常并不一致。例如，Style3 的风格示例图，整体是蓝白黑三色调，但是得到的风格化后的结果图带有大部分的米黄色色调。Style2 中也存在类似现象。这种色调不一致的现象反复出现。经过多次实验验证发现该算法测试生成的结果图颜色布局与训练过程中最后一张风格图相关（主要在颜色上受影响），导致风格化后结果图与风格示例图具有不一致的颜色布局。从图1 中便可见一斑。风格完全不同的Style1、Style2、Style3 对应的风格化结果图在颜色色调上却很接近。因此，此方法在迁移效果上，仅做到了纹理风格的不完美迁移，并没有完全做到风格的任意迁移。

为了避免风格化结果图出现明显的不协调像素缺块，且同时实现风格化结果图与风格图的颜色布局相一致，本文主要借鉴Gatys 等人[1]提出的Gram 矩阵，在风格统计量和损失函数等方面对Shen 等人[17]方法进行了改进。通过实验对比，本文改进的模型能够较完美地解决前述两方面的问题，实现良好、快速有效的任意风格任意内容的快速迁移。

本文的主要贡献在于：（1）将Gram 矩阵引入基于元网络的任意风格迁移算法框架并进行改进，有效解决了基准方法的明显缺陷，同时实现实时有效的任意内容任意风格的单图像风格迁移。（2）对于风格迁移问题，通过充分的实验验证、理论分析，进一步厘清了Gram 矩阵统计量在算法收敛性和视觉效果上优越性所在。

2 基于Gram 矩阵的元网络任意风格迁移

2.1 元网络

Shen 等人[17]提出的元网络为两层全连接层，输入是风格图的组合特征向量，输出向量用于对图像转换网络（image transformation network，ITN）各卷积层的卷积核进行权重分配，以达到不同的风格对应不同的卷积核，最终实现任意风格迁移的目的。他们将VGG16[18]中Relu1_2、Relu2_2、Relu3_3、Relu4_3 卷积层对应的特征映射图，求均值和方差，然后串联成一维向量，输入至元网络的第一层全连接层。输入向量的维度大小等于(64+128+256+512）×2=1 920。为了避免元网络参数过大，第二层全连接层采用分组全连接层的思路：每组全连接输入128 维，各组输出对应分配到特定卷积层权重。图像转换网络的卷积层，包括下采样卷积层2 层、残差卷积层10 层、上采样反卷积层2 层。因此，元网络第二层的全连接层输入大小为14×128=1 792 维。该方法的具体元网络细节如图2 所示，其他细节在此不再赘述。

虽然均值和方差计算非常简单，但作为风格统计量，其包含的信息量有限，不足以表征风格图的特点，这也是Shen 等人[17]的方法存在前述缺陷的主要因素。本文主要借鉴Gatys 等人[1]提出的Gram 矩阵，改变了Shen 等人[17]方法中元网络输入信息和风格损失计算方式。本文不再使用特征图的均值和方差，而是使用VGG16 的Relu1_2、Relu2_2、Relu3_3、Relu4_3 的特征映射图计算Gram 矩阵。

相对于均值和方差，直接使用Gram 矩阵输入至元网络中，会使全连接层的参数变得非常大，整个网络框架几乎无法放进主流GPU（如11 GB显存的GTX 1080TI）。为了既能最大程度保留Gram 矩阵信息丰富的特点，又能适当缩小网络参数规模，把尺寸最大的Relu4_3 层的Gram 矩阵（大小为512×512）进行了下采样，采用平均池化将其大小变为原来尺寸的1/4。由于Gram 矩阵式对称阵，选择Gram 矩阵的上三角或下三角数值作为特征，再结合分组全连接的思路，最终能将整个网络控制在合理参数规模范围以内。改进后的元网络输入信息是能够有效表征风格特点的Gram 矩阵，由4 个Gram 子矩阵64×64、128× 128、256×256、256×256 串联而成。

Fig.2 Meta network architecture图2 元网络框架

2.2 内容损失

在内容损失函数计算方面，本文保持和Shen 等人[17]方法一致。具体地，将风格化结果图和原始内容图分别经过在ImageNet 预训练好的VGG16 网络，计算它们相同层对应的特征图之间的欧式距离。内容损失公式如式（1）所示：

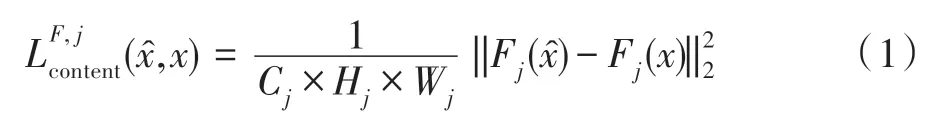
其中，x为输入的内容图像，像，Fj(x)是处理图像x时VGG16 网络第j层的特征图，尺寸为Cj×Wj×Hj。

预训练好的VGG16 网络参数在整个训练和测试过程中保持固定。

2.3 风格损失

在风格损失计算方面，Shen 等人[17]计算风格化结果图y分别经过VGG16 的Relu1_2、Relu2_2、Relu3_3、Relu4_3 四层后的特征图的均值和方差的欧式距离。

Shen 等人[17]利用均值和方差代替Gram 矩阵作为风格统计量的做法，虽然也能使风格化后结果图具有与风格示例图相似的纹理，且相对于Gram 矩阵计算速度更快，计算量更小，但是经常很容易导致结果图的整体风格布局与风格图不相匹配或者匹配度较低，如Huang 等人[16]的方法便采用了均值和方差作为损失函数。该方法的风格化结果图像均带有明显的块状，以至于在视觉上他们的结果与其他方法存在差距。均值和方差作为风格统计量并不适用于所有的框架。

Gram 矩阵计算图像特征之间的偏心协方差矩阵（即没有减去均值的协方差矩阵）。定义矩阵Ψ表示大小为C×W×H特征图Fk(x)。

令Ψ=[f1,f2,…,fC]，其中fi∈ℜWH是特征图Fk(x)第i={1,2,…,C}个通道层对应的特征平面的所有元素构成的列向量。Gram 矩阵如式（2）所示：

特征图Fk(x)的方差和均值表示为σ=[σ1,σ2,…,σC]，μ=[μ1,μ2,…,μC]，其中均值向量元素，方差向量元素σi=(fi-μiI)T(fi-μiI)。类似地，可以计算协方差：

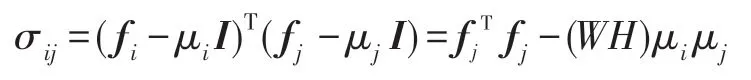
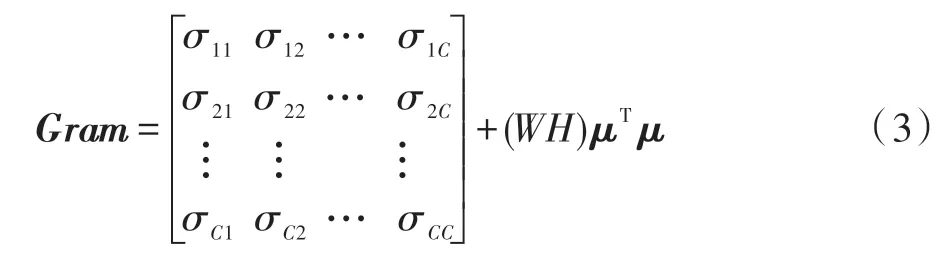
从它们的数学计算过程也不难看出，Gram 矩阵计算是均值和方差计算的一般泛化形式，包含了比方差和均值更丰富的信息。Gram 矩阵可以度量特征各维度自身特性以及各维度之间的关系，能够更全面表示特征图Fk(x)的结构特性，反映风格的整体属性。相比之下，均值和方差只能反映特征维度自身的特性。

采用能更好适用于风格特征表示的Gram 矩阵作为风格损失，虽然会使计算量变大，也会使网络整体框架变得更大，但是只要能进行合理优化，是可以做到性能与计算代价的平衡。

风格损失如下：

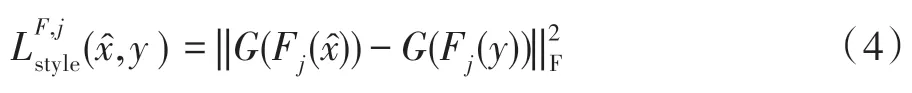
其中，G表示在VGG16 网络中第j层的特征图的Gram 矩阵。

需要指出的是，虽然在元网络输入表示时，对Gram 矩阵进行池化操作，但在训练时，因为不涉及到网络参数大小的问题，采用了原始大小的Gram 矩阵计算风格损失。

网络最终的总损失函数如式（5）所示。

其中，超参数α和β分别为内容权重和风格权重。

作为用户控制参数，提高α/β的比值会使风格化结果图注重内容信息，视觉上更偏向于内容图像；减小α/β风格权重会使风格化结果图像注重风格信息，使其更具有风格化。

2.4 神经风格迁移

图像转换网络（ITN）的权重（除了第一层和最后一层）由元网络分配。改进模型的整体框架如图3所示。

图3 所示的整体网络的数据流向为：（1）网络输入有内容图像和风格图像。（2）红色数据流向指示，风格图像经过预训练VGG16 网络。其中，若干层卷积特征计算Gram 矩阵输入元网络。元网络的输出为图像转换网络（ITN）进行权重赋值。（3）蓝色数据流向指示，内容图像经过风格权重赋值的图像转换网络，生成结果风格化图像。（4）绿色数据流向指示，训练时，风格化图像结果经过VGG16 网络，在对应卷积层上计算与风格图像的风格损失，计算与内容图像的内容损失。

3 实验

3.1 实验细节

实验所使用的内容图像来自于Microsoft COCO数据集，风格示例图来自于WikiArt 数据集。其中，内容图像大约80 000 张，风格图大约有8 000 张。在训练过程中，先把内容图像缩放到[256,480]的区间范围，然后再随机剪裁成256×256 尺寸的图像。优化器采用Adam，网络训练学习率固定为0.001，批量大小Batchsize 设置为2。每20 轮循环，随机更换一张风格图。

在内容损失方面，重点考虑图像高层语义相似性计算，因此采用预训练好的VGG16的Rule3_3层的特征图来计算内容损失；在风格损失方面，选取预训练好的VGG16的Relu1_2、Relu2_2、Relu3_3、Relu4_3四层的特征图的Gram 来计算风格损失；ITN 网络结构保持与Shen 等人[17]方法一致。

由于内容损失和风格损失计算的量值比例的原因，将α/β比值作为用户控制参数。在图4 展示了不同的α/β值的效果。当比值为2×10-5时，能够做到内容与风格平衡协调。因此，为了调参的方便，后续实验均采用此设置。式（5）中内容权重α=1，风格权重为β=2×105。

3.2 实验对比

为了评价改进方法的有效性，与其他主流的风格迁移方法进行了对比。

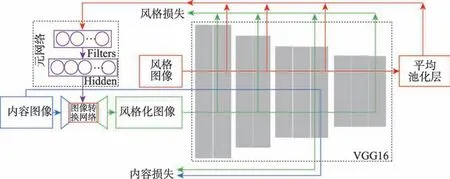
Fig.3 Model architecture图3 模型结构

Fig.4 Effect of different weight ratios图4 不同权重比值的效果

在损失收敛方面，将本文方法与Shen 等人[17]的方法进行了比较，如图5 所示。在内容损失方面本文方法更加稳定，从风格损失方面可以看到本文方法收敛得更好。主要归因于Gram 矩阵在风格损失的计算数值上较均值和方差更稳定。

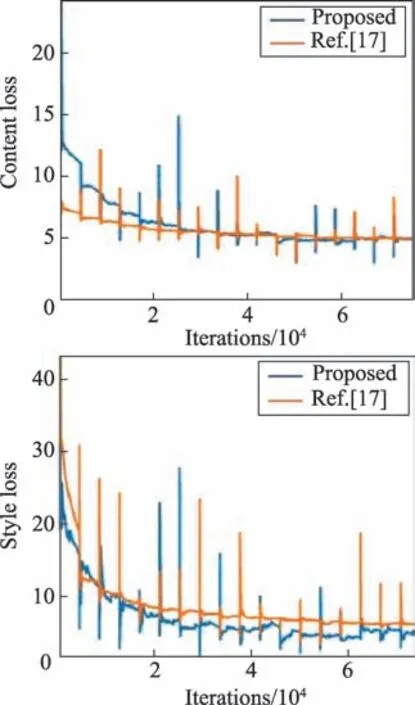
Fig.5 Loss convergence图5 损失收敛情况

为了验证Gram 矩阵作为风格损失计算的必要性，继续进行了对比实验。Johnson 等人[9]提出的框架是风格迁移领域中最基础、最通用的方法之一。用均值和方差作为损失替代该算法框架中的Gram矩阵，并且将超参数调整到实验最优，结果如图6 所示。除却伪影，从纹理和颜色方面可以看出使用均值和方差损失的效果与Gram 矩阵差距较大。均值方差损失在风格迁移中的效果并不理想。通过前述理论分析、实验佐证，进一步肯定了采用Gram 矩阵作为风格损失和特征统计量在算法收敛性和视觉效果方面的优越性。

Fig.6 Comparison of effects of different losses图6 不同损失的效果比较

Fig.7 Stylized effect results of proposed model(Compared with Fig.1)图7 本文模型的风格化效果图（与图1 对比）

在图像风格化的质量与效果方面，图7 展示了本文改进方法结果的优越性。相比图1中Shen等人[17]方法的实验结果，无论在图像缺块问题，还是在颜色色调布局不一致方面，在本文改进的方法中都得到了较好的解决。

图8 所采用的风格示例图，均为Shen 等人[17]和本文的方法在训练过程中从未训练过的风格图。不难看出，在视觉纹理分布上，本文方法与Gatys 等人[10]的方法基本相似，都比Shen 等人[17]的方法纹理更丰富；同时，本文在内容上比Gatys 等人[10]的方法视觉表现更好；在颜色色调方面，本文方法也取得了比其他方法明显更好的效果。

为了更多地验证本文方法的适应能力，图9 展示了使用本文方法进行风格迁移的更多效果图。所有生成的图片尺寸均为256×256，不难看出，本文方法取得了不错的结果，可以适用于不同风格、不同内容的场景。

Fig.8 Contrast of stylized effect charts of different methods图8 不同方法的风格化效果图对比

Fig.9 More stylized results generated by proposed model图9 更多本文模型生成的风格化结果

表1 记录了五种主流风格化迁移算法的迁移速度。在GTX1080TI 上进行测试，测试的风格图像和内容图像大小均为256×256。可以看出来，本文方法虽然比Shen 等人[17]的原方法慢了3 ms（主要是计算Gram 矩阵的原因），但几乎是可以忽略不计的程度，仍然可以实现快速的风格迁移。

Table 1 Comparison of transfer speed for different methods表1 不同方法的迁移速度对比

4 结束语

本文在Shen 等人[17]的基础上解决了他们的方法遗留下的风格结果图存在的不协调缺块和颜色布局与目标风格图不一致等问题，提出了基于Gram 矩阵风格统计量的元网络风格迁移改进网络，并通过合理优化避免了传统Gram 矩阵带来网络参数整体过大的问题。通过实验验证，使用本文方法不仅不会出现风格化图像不协调缺块的问题，而且还可以完美保持与风格图像的颜色布局一致。本文方法进行风格迁移后的图片在视觉效果上比原方法具有更好的效果和表现，可以实现任意风格任意内容的快速风格迁移。