秘密区间与阈值的保密判定*

2020-05-13李顺东王文丽

计算机与生活 2020年5期

成雯，李顺东，王文丽

1.陕西师范大学计算机科学学院，西安 710119

2.陕西师范大学数学与信息科学学院，西安 710119

1 引言

安全多方计算（secure multi-party computation，SMC）这一概念首先由Yao[1]在20 世纪80 年代以百万富翁问题提出，经过Goldreich[2-3]、Franklin[4]和Gennaro[5]等学者的发展，安全多方计算已经成为密码学领域的研究热点，是信息安全保护的关键技术。安全多方计算是指两方或多方在不泄露各自私有数据的基础上保密地进行合作计算，发挥数据在信息时代的经济[6-8]、科学计算[9-10]、社会[11-12]等方面的价值。安全多方计算协议也被广泛地应用于秘密共享[13-14]、电子商务[15]等方面。

区间的保密计算具有重要的理论意义，从目前的研究看，大致可以将区间的保密计算分为两类：

第一类问题是目前研究最多的，可以描述为参与计算的一方拥有区间，另一方拥有私有数据，两方合作保密判定点与区间的位置关系。这类问题已经有过很多成果。Nishide 等人首先在文献[16]中将区间问题作为比特分解协议的应用，但并没有对区间问题进行深入的分析。文献[17]利用计算几何定理和基本算术知识，设计了两个高效的有理数区间保密计算协议。文献[18]利用编码原理和级联异或，设计了整数点和离散的整数区间的保密判定协议；将实数转换为整数，设计了实数点和连续的实数区间的保密判定协议。文献[19]利用多项式和整数向量内积符号的判定，设计了高效的有理数保密计算协议和有理区间保密计算协议。

第二类问题可以描述为两方或多方合作生成秘密区间，另一方拥有私密数据，任何人对区间信息一无所知，在此基础上对秘密区间与阈值进行保密判定。此问题在密码学领域有重要的理论意义，在保密插入、商品交易等应用场景中也具有实际意义。文献[20]曾将判定点与线段的关系转化为判定点与线段两端点形成的区间的关系，但该协议不能区分点与区间的全部位置关系以及不能抵抗合谋攻击。而本文设计的协议不仅能区分阈值与秘密区间的全部位置关系，且均能抵抗合谋攻击，并将秘密区间问题由两方合作生成扩展到多方合作生成。

百万富翁问题可以描述为：两个百万富翁Alice和Bob 想知道他们谁拥有的财富更多，但他们都不想向对方泄露自己的财富。数学描述为：Alice 和Bob各自拥有数据x、y，他们想保密地判断x、y的大小。Paillier密码系统的明文空间为ZN。(ZN,+)构成一个加法群，在这个群里是没有正负数之分的，但如果限制实际处理的明文m都在[0,)之内，即m∈{0,1,…,-1}，如果x+y=0 modN，而0 ＜x＜，那么一定有y＞。在这种情况下y是x的加法逆元，如果认为x≥0，那么y就可以看作负数。进一步假设x,y＜，如果(x-y) modN＜，则x＞y；如果(xy) modN＞，则x＜y。利用这个原理可以设计出半诚实模型下百万富翁问题的安全多方计算协议。

秘密区间与阈值的保密判定问题直观上的解决思路就是比较阈值与秘密区间两个端点的大小关系。针对两方合作生成秘密区间，只需将秘密区间的两个端点与阈值进行保密比较，即调用两次百万富翁协议；针对多方合作生成秘密区间，通过多次调用百万富翁协议可以得到秘密区间的两个端点，再调用两次百万富翁协议来比较阈值与秘密区间端点的关系。但是多次调用百万富翁协议不仅泄露了秘密区间的端点值，而且增加了计算复杂性和通信复杂性。为了保护秘密区间不被泄露以及提高效率，本文利用编码原理并结合Lifted ElGamal 同态加密算法，提出了优化协议。

本文贡献如下：

（1）提出了秘密区间与阈值的保密判定这个新的问题，并针对该问题的不同应用场景分别给出了高效安全的解决方法。

（2）针对两方合作生成秘密区间，基于Paillier 同态加密算法设计了一个协议，利用模拟范例证明了方案的安全性，并进行了效率分析和实验验证。

（3）针对多方合作生成秘密区间，利用编码原理并结合Lifted ElGamal 同态加密算法，提出了优化协议，避免了多次调用百万富翁协议，保护了秘密区间信息且提高了效率。

（4）本文设计的协议不仅能区分阈值与秘密区间的全部位置关系，且均能抵抗合谋攻击，并将秘密区间问题由两方合作生成扩展到多方合作生成。

（5）对区间保密计算问题进行了扩展，针对秘密区间问题进行研究，并给出了秘密区间与阈值保密判定的应用实例。

2 预备知识

2.1 安全性定义

半诚实参与者：一般而言，半诚实参与者是指参与者会严格地执行协议，但可能会通过保留的中间结果试图推出其他参与者的私有数据或其他一些信息。

假设有n个参与者分别拥有私密数据xi(i∈{1,2,…,n})，他们共同执行协议π的计算函数f(x)：

并得到最终结果。令X=(x1,x2,…,xn)，在协议执行过程中，将参与者得到的消息序列记为：

定义1（半诚实协议的安全性[21]）设f=f({0,1}∗)n→({0,1}∗)n是概率多项式函数。fi(x1,x2,…,xn)是f(x1,x2,…,xn)中的第i个元素，令Pi表示第i个参与者，设I={Pi1,Pi2,…,Pis}⊆{P1,P2,…,Pn}是任意参与者的子集，fI(x1,x2,…,xn)代表序列fi1(x1,x2,…,xn),fi2(x1,x2,…,xn),…,fis(x1,x2,…,xn)，outputπ(x) 表示所有参与者执行完协议π后的结果。假设参与者都是半诚实的，如果说协议π保密地计算n元函数f，那么存在概率多项式时间算法S，使得对于任意I都有下列式子成立：

2.2 概率加密算法

一个公钥加密方案[22]一般由KeyGen、Encrypt、Decrypt 三个算法组成。

（1）KeyGen

选取安全参数λ，输出私钥sk、公钥pk、明文空间M和密文空间C，即：

（2）Encrypt

给定公钥pk和明文m∈M，输出相应的密文c∈C：

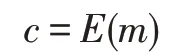
（3）Decrypt

给定私钥sk和密文c，输出相应的明文m：

概率加密算法在加密过程中需要选择随机数r∈M参与运算，因此如果选用不同的随机数r，对于相同的明文m也会产生不同的密文c。

Paillier、ElGamal 等是常用的概率加密算法，这些算法具有的同态加密性[23]可以帮助解决很多保密计算问题。例如Paillier 加密算法具有加法同态性，具体如下：

Lifted ElGamal 加密算法是在ElGamal 加密算法上加以修改的，它具有加法同态性，具体如下：

E(m1)E(m2)=E(m1+m2)

2.3 门限密码体制

在安全多方计算中可以用门限解密[24]来抵抗合谋攻击。因为本文需要抵抗n-1 个参与者的合谋攻击，所以需要的是(n,n)门限。公钥由n个参与者联合生成，而私钥是由这些参与者分享的。用公钥加密的消息必须由n个参与者合作才能完成解密。Paillier、ElGamal 等密码系统都可以用来构造门限密码系统，下面以Lifted ElGamal 为例给出门限密码系统的具体构造：

（1）KeyGen

选取安全参数λ并产生素数p，选择的一个生成元g。每个参与者Pi随机选取ki∈作为私钥，并计算hi=modp。n个参与者计算公钥：

（2）Encrypt

为加密明文M，选择随机数r，按照下式计算密文c：

（3）Decrypt

对于密文c=(c1,c2)，每个参与者Pi按照下式解密：

Lifted ElGamal门限密码系统在解密过程中得到的是gM，涉及到离散对数计算，为了计算方便，一般取g=2，gM＜p。当M的值不太大时（本文协议2 中M的取值只有0，1），很容易从2M中获得M。可以预先计算所有的结果，在解密时通过查表快速解密。

3 两方合作生成秘密区间与阈值的保密判定

两方合作生成秘密区间与阈值的保密判定问题具有广泛的应用背景。考虑如下场景：Alice 拥有数x，Bob 拥有数y，Alice 和Bob 合作构成区间[x,y]或[y,x]，Carol 拥有数z，现要保密得到z的插入位置，即z在区间左侧、在区间内还是在区间右侧。

问题描述：Alice 拥有x，Bob 拥有y，Carol 拥有z(x,y,z＞0)，保密地判断z与秘密区间I=[min{x,y},max{x,y}]的关系。

解决思路如下：直观上考虑，要保密地判断z与秘密区间I的关系，就是要保密比较阈值与区间端点的关系。因此基于以下事实设计了协议1。

事实假设Alice 拥有数据x，Bob 拥有数据y(0 ≤x,y＜)，要保密判断x、y的大小。将x和Ny分别用Paillier 加密算法的公钥加密得到E(x) 和E(N-y)，令C=E(x)E(N-y)，用私钥解密C，记解密结果为w=D(C)，则有下面结论：

证明由Paillier 加密算法定义以及加法同态性，可知：

当用私钥解密时，解密结果为：

分析如下：为了描述方便，定义T(z,I)（以下简称T）如下：

协议1两方合作生成秘密区间与阈值的保密判定

准备阶段：选定安全参数k，参与者P3运行Paillier 加密算法，生成公钥pk和私钥sk，P3向P1、P2公布生成的公钥（以下所涉及到的随机数均属于

（1）P3用公钥加密N-z得到E(N-z)并发送给P1、P2。

（2）P1选取随机数r11，用公钥加密x得到E(x)，计算：

并将U发送给P2。

（3）P2选取随机数r12、r22，用公钥加密y得到E(y)，计算：

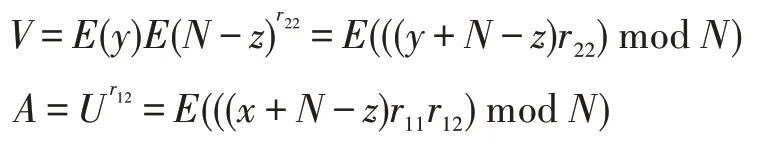
并将V、A发送给P1。

（4）P1选取随机数r21，计算：

并将A重随机化后记为C，选取随机置换φ作用于B、C，得到J、K并发送给P3。

（5）P3解密P1发来的数据得到u=D(J)，v=D(K)，按照下述情况输出T：

注：由上述事实可知，在利用Paillier 加密算法的性质保密比较x、y的大小时，需要限制x、y的范围为0 ≤x,y＜。在协议1 中，为了保护数据隐私以及得到计算结果，需要计算(x+N-z)r11r12和(y+Nz)r21r22。现令x′=xr11r12，z′=zr11r12和y′=yr21r22，z″=zr21r22，与事实中x、y相对应，就需要限制0 ≤x′,z′＜和0 ≤y′,z″＜，因此协议1 中选取的数据和随机数都属于[0,]。

正确性分析：两方合作生成秘密区间与阈值的判定问题可以描述为阈值与区间端点比较问题，基于事实可以正确得到秘密区间与阈值的关系。

安全性分析：

（1）考虑合谋

①P1、P2合谋想获取P3的信息z。因为只有P3可以解密，P1、P2只能得到P3的密文E(N-z)，而加密算法是语义安全的，E(N-z)和某个随机数是不能被区分开来的，因此协议1 可以抵抗P1、P2合谋。

②P3参与合谋，此时P1、P2的地位是平等的，能力是相同的，因此只对其中一种情况证明协议1 是安全的。假设P2、P3合谋想获取P1的值x，P2、P3能够在协议过程中获得密文J、K，假设：

在这两个等式中，y、r12、r22、z是P2、P3的保密数和随机数，x、r11、r21是3 个未知变量。P2、P3不能通过这两个方程来确定P1的值x。因此协议1 可以抵抗P2、P3合谋。

同理可证协议1 可以抵抗P1、P3合谋。

（2）不考虑合谋

假设参与者都不合谋，对于P3来说，存在6 个未知变量，他不能通过两个方程来确定P1、P2的值；对于P1、P2来说，仅知道自己的数据、T值和一些密文，得不到任何信息。

因此协议1 是安全的，并且可以抵抗合谋攻击。

定理1协议1 在半诚实模型下是安全的。

证明下面通过构造满足式（1）的模拟器S来证明定理1。

（1）假设P3参与合谋，以P2、P3合谋为例，则最大合谋者集合为I={P2,P3}。此时：

给定输入(I,(y,z),fI(X))，S随机选择x′使得：

模拟器S用x′、y、z按照协议1 做如下模拟：

并将A′重随机化后记为C′，选取随机置换φ作用于B′、C′，得到J′、K′。

（2）P3不参与合谋，P1、P2只知道P3发布的密文E(N-z)，而加密算法是语义安全的，密文和某个随机数是不可区分的，可以用类似的模拟证明协议1的安全性。

因此，该协议对于半诚实参与者是安全的。□

4 多方合作生成秘密区间与阈值的保密判定

考虑以下场景：顾客想将古董卖给古董行，有多家古董行都想购入该古董，现要保密地判断顾客估价是否符合该古董的市场估价范围。每家古董行都有一个估价，市场估价范围[x,y]由多家古董行的最低价x和最高价y构成。如果估价在[x,y]内，则顾客和古董行进一步商量，达成交易；否则顾客可以继续调整估价或放弃交易。因此设计这样的协议不仅能保护用户的私有数据，同时能节省不少时间和成本，在生活中是具有实际意义的。

问题描述：假设参与者Pi(i∈{1,2,…,n})拥有私密数据xi，Alice 拥有数据z，保密地判断z是否在n个参与者合作构成的秘密区间I=[min{x1,x2,…,xn}，max{x1,x2,…,xn}]内。

解决思路如下：n个参与者数据中的最小值和最大值分别为秘密区间I的两个端点，得到I后再保密地判定阈值与秘密区间的关系。可以借鉴文献[25]中保密替换的思想，但并不需要求出最小值和最大值，而直接得到保密的区间范围，然后根据z值取对应列元素进行相加即可判断z与秘密区间I的关系。

多个数据求最小值的方法如下：

编码方法1n个参与者各自拥有私密数据xi(1 ≤xi≤m)，将数据xi按照以下方法表示为对应的数组Xi=(xi1,xi2,…,xim)，其中：

参与者P1按照该方法得到数组X1=(x11,x12,…,x1m)，即数组前面有x1-1 个0，后面有m-x1+1 个1。参与者Pj(j∈{2,3,…,n})用m-xj+1 个1 替换前一个参与者发来的数组的后m-xj+1 个元素，得到新的数组Xj，而其他元素保持不变。最后求得的数组Xn=(xn1,xn2,…,xnm)中0 元素的个数恰好等于最小值减1 的值。

多个数据求最大值的方法如下：

编码方法2n个参与者各自拥有私密数据xi(1 ≤xi≤m)，将数据xi按照以下方法表示为对应的数组Yi=(yi1,yi2,…,yim)，其中：

参与者P1按照该方法得到数组Y1=(y11,y12,…,y1m)，即数组前面有x1个0，后面接着有m-x1个1。参与者Pj(j∈{2,3,…,n})用xj个0 替换前一个参与者发来的数组的前xj个元素，得到新的数组Yj，而其他元素保持不变。最后求得的数组Yn=(yn1,yn2,…,ynm) 中0元素的个数恰好等于最大值。

例如，参与者Pi(i∈{1,2,3})分别拥有数据x1=5，x2=3，x3=9，令m=10。

P1分别利用编码方法1、2 构造数组如下：

由P2替换后为：

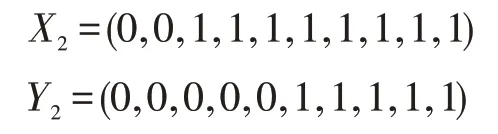
由P3替换后为：

则参与者合作构成的秘密区间为：

Alice 拥有数据z(1 ≤z≤m)，只要将数组对应第z列元素进行相加记为T，即可根据下述情况判断z与秘密区间I的关系。

（1）当T=0 时，z在秘密区间左侧；

（2）当T=1 时，z在秘密区间内；

（3）当T=2 时，z在秘密区间右侧。

协议2多方合作生成秘密区间与阈值的保密判定

输入：参与者Pi(i∈{1,2,…,n})各自输入数据xi，Alice输入z。

输出：T(z,I)（以下简称T）。

准备阶段，运行Lifted ElGamal 加密系统构造的(n+1,n+1) 门限密码系统，参与者Pi(i∈{1,2,…,n})，Alice 分别选择私钥ki(i∈{1,2,…,n+1})，并选择公共参数g、p联合生成公钥：

（1）参与者P1分别按照编码方法1、2 将x1表示为数组X1、Y1，并将E(X1)=(E(x11),E(x12),…,E(x1m))，E(Y1)=(E(y11),E(y12),…,E(y1m))发送给P2。

（2）令c=(c1,c2,…,cm)=(E(x11),E(x12),…,E(x1m))，d=(d1,d2,…,dm)=(E(y11),E(y12),…,E(y1m))。

（3）参与者Pj(j∈{2,3,…,n})计算如下：

①参与者Pj根据数据xj按照上述方法分别对数组c、d中的元素进行替换。

②对数组c、d进行重随机化。

③更新数组c=(E(xj1),E(xj2),…,E(xjm))，d=(E(yj1),E(yj2),…,E(yjm))。

（4）参与者Pn将数组c=(E(xn1),E(xn2),…,E(xnm)),d=(E(yn1),E(yn2),…,E(ynm))发送给Alice。

（5）Alice 根据自己的数据z分别选择数组c、d中对应的第z列元素，计算如下：

并将U公布。

（6）n个参与者和Alice 联合解密T=D(U)，即可以得到z与秘密区间I的关系。

正确性分析：协议2 的正确性可由门限解密的基本原理和第4 章协议的基本原理得到保证。

安全性分析：协议2 的安全性是基于门限密码体制的安全性，因此协议过程中公布的密文，如果有任何少于n个参与者进行解密的话都无法得到正确结果，也就是说协议2 是可以抵抗合谋攻击的。

定理2协议2 在半诚实模型下是安全的。

定理2 的证明与定理1 类似，此处省略具体证明过程。

5 效率分析

秘密区间与阈值的保密判定问题研究成果较少，文献[20]涉及3 个参与者，且秘密区间由两方合作生成，与本文协议1 情况类似，对协议1 与文献[20]进行效率比较。而目前没有多方合作生成秘密区间与阈值保密判定的协议，因此协议2 没有与其他文献进行效率比较。

5.1 计算复杂性

首先分析协议的计算复杂性。为了方便计算，在分析协议的计算复杂性时只考虑最耗时的模指数运算。文献[20]、协议1 选用的是Paillier 加密算法，加密、解密一次均需要两次模指数运算，计算一次密文模指数需要一次模指数运算。协议2 选用的是Lifted ElGamal 门限密码系统，加密一次需要三次模指数运算，解密运算的模指数运算次数与参与解密的人数有关。

文献[20]共需要18 次模指数运算。协议1 加密、解密、密文模指数、重随机化分别需要6 次、4 次、4次、2 次模指数运算，共需要16 次模指数运算。协议2 中假设所有数据不超过m，加密过程最多需要6mn次模指数运算，解密、重随机化过程分别需要(n+2)次、4m(n-1) 次模指数运算，因此协议2 最多需要10mn-4m+n+2 次模指数运算。