基于柱面微透镜阵列的激光匀化系统设计及实验研究

周 叶,祝启欣,黄中亚,骆崛魁,李 成

(武汉锐科光纤激光技术股份有限公司,湖北 武汉 430075)

1 引 言

随着激光技术的不断发展,激光以其独特的优势被广泛应用于工业、医疗、军事、科研等诸多领域[1]。不同的应用场合对激光光斑形状及空间分布有着不同的需求,通常激光光强呈高斯分布,由于光能量分布不均,在与物质相互作用过程中光能利用率较低,并且很容易造成局部温度过高损坏材料或影响加工效果。具有光强均匀分布的平顶激光光束是目前激光应用领域的一大研究热点,在激光切割、焊接、熔覆等激光加工工艺、非线性激光抽运技术、半导体基片退火、光学全息、激光照明、激光打印等领域中具有广泛的应用需求[2-4]。利用光束整形技术可以获得平顶型光场分布的激光光束,常用空域的光束整形方法主要有非球面透镜组[5]、衍射光学元件[6-7]、双折射透镜组[8]、多边形匀化棒[9-10]、微透镜阵列[11-12]、液晶空间调制器[13]等方法。其中微透镜阵列整形系统具有结构简单、传输损耗小、损伤阈值高、对入射光强分布要求小等优点被广泛应用。目前,国内外学者主要围绕形成斑点模式的矩形微透镜阵列进行了相应的研究[14-16],有关线光斑的报道较少,本文设计了一种基于柱面微透镜阵列的光束匀化系统,分别从几何光学与波动光学出发,对成像系统的光束匀化特性进行了理论分析,最后通过搭建实验系统获得了光斑长度可调的均匀线光斑,同时研究了不同参数的柱面微透镜阵列组合下的光斑匀束特性,实验结果与理论相吻合,这种长度灵活可调的均匀线光斑在半导体基片退火工艺、激光抛光、激光淬火和激光清洗等领域具有重要的应用价值[17]。

2 成像型柱面微透镜阵列光束匀化系统设计

2.1 原理简介

成像型微透镜阵列光束匀化系统如图1所示,准直高斯光束经过微透镜阵列LA1后被分割为多个微小的子光束,各子光束经第二列微透镜阵列LA2与球面傅里叶透镜FL所组成的物镜系统后分别成像在球面透镜的后焦面FP上,并在同一区域中叠加,实现了光斑能量的均匀化,使光场近似平顶分布。系统中两片微透镜阵列的透镜单元大小相同,均为为PLA,其中微透镜阵列LA1的焦距为fLA1,微透镜阵列LA2的焦距为fLA2,两微透镜阵列之间的间隔为d。傅里叶透镜FL的焦距为fFL,微透镜阵列LA2与傅里叶透镜FL之间的距离记为d0,焦平面上匀化光斑长度为DFT。

图1 成像型微透镜阵列光束匀化系统Fig.1 Schematic of imaging microlens array system

2.2 理论分析

2.2.1 基于矩阵光学的理论分析

基于矩阵光学理论,在傍轴近似的条件下,对初始光线在空间中的传播过程进行光线追迹。光线沿z轴方向传播,入射光的光线矩阵可以表示为r(PLA,θ1),依次经过后方的光学元件及自由空间传输后,在聚焦透镜的后焦面上成像,整个传播过程可以通过初始光线矩阵依次与传播过的光线矩阵相乘得到,最终在焦平面上的成像光线矩阵可以表示为:

(1)

当入射光为准直平行光,即θ1=0时,可得焦平面上的光斑长度:

(2)

从式(2)可以看出成像光斑的长度与系统各光学元件的参数以及两列微透镜阵列间距均相关,改变系统各个参数可以实现不同的成像光斑长度,在光学元件确定的条件下,改变微透镜阵列间距可以灵活地调节光斑长度。

2.2.2 基于傅里叶光学的理论分析

上述理论主要基于几何光学的分析方法,简单地对边缘光线进行了追迹,推导得到成像光斑长度,为了更加准确地分析像平面上光强分布情况,需采用傅里叶光学的方法进行光场分析。入射光为准直后的高斯光束,垂直入射到微透镜阵列LA1上,设微透镜阵列LA1和LA2均由(2n+1)个子透镜组成,子透镜孔径为p,焦距为f,傅里叶透镜焦距为fF,这种情况下,紧靠微透镜阵列前平面上的光场分布为一常数,设为1,微透镜阵列传输函数为:

(3)

(4)

(5)

设d=f,则二次相位因子和变换函数中的二次位相因子相消,得到:

(6)

(7)

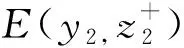
(8)

以上理论结果是在两列微透镜间距d为第一列微透镜阵列LA1的焦距f的情况下得到的焦平面上的光强分布情况,式(8)中,rect矩形函数可以看成子透镜的衍射作用光场,sinc函数可以看成是多缝干涉作用光场。因此,成像光斑可以看成是由单个透镜的衍射与(2n+1)个狭缝的多缝干涉共同作用的光场分布。

2.3 仿真分析

通过设置相应的参数进行数值模拟,仿真分析了成像光斑的光强分布,如图2所示,从图中可以看出,平面入射光束经成像型微透镜阵列系统后,形成了平顶分布的矩形光斑,光斑表面呈现明暗相间的强度分布,这种现象主要是由于光束经微透镜阵列多个子透镜的分束后,在傅里叶透镜后焦面产生了多光束干涉的原因,而光斑轮廓主要由矩形函数决定,由于微透镜阵列是由多个柱面子透镜紧密排列的结构,各个子单元之间会存在间隙,从而造成透镜边缘处发生衍射,使得光斑轮廓出现了边缘凸起的现象。

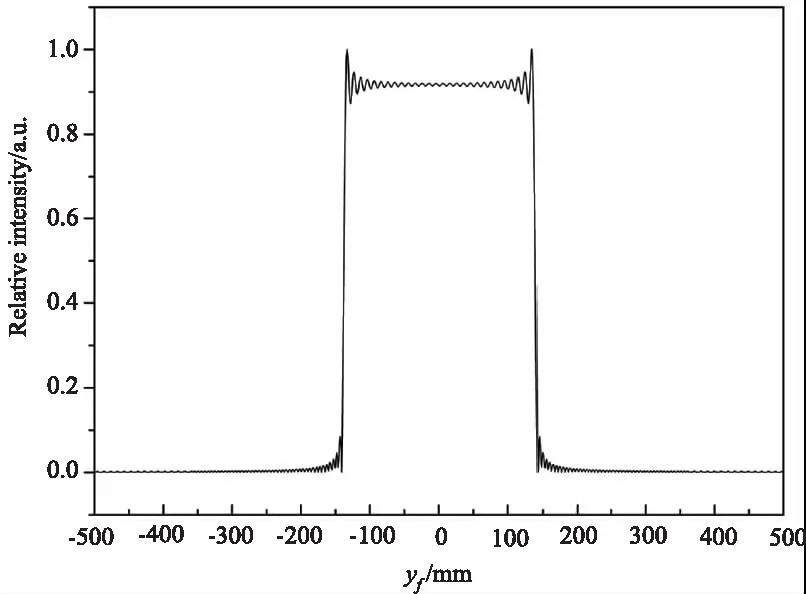
图2 目标平面处光强分布Fig.2 Intensity distribution at the target plane

2.3.1 成像光斑与子透镜孔径的关系

保持微透镜阵列的子透镜焦距f一定,改变子透镜孔径p的大小,图3为目标平面处光场分布与微透镜阵列子透镜孔径p的关系,可以看出,成像光斑长度随着子透镜孔径的增大而增大,光斑均匀度也随之提高。分析原因,这是由于当子透镜孔径增大时,单透镜的菲涅尔衍射效应减弱,同时子光束的干涉作用也随之减弱,使得光束均匀度提高。

图3 不同子透镜孔径时光强分布Fig.3 Intensity distribution in different sublens apertures

2.3.2 成像光斑与子透镜焦距的关系

保持微透镜阵列的子透镜孔径p一定,改变子透镜焦距f的大小,图4为目标平面处光场分布与微透镜阵列子透镜焦距f的关系,可以看出成像光斑长度随着子透镜焦距的增大而减小,而光斑均匀度没有变化。这主要是由于焦距改变时,对光场的衍射效应及干涉效应不会造成影响,因此,光斑均匀性不会发生改变。

图4 不同子透镜焦距时光强分布Fig.4 Intensity distribution in different sublens focuses

3 成像型柱面微透镜阵列光束匀化系统实验研究

3.1 实验装置

基于柱面微透镜阵列的半导体激光匀化系统实验装置如图5所示,采用波长为1064 nm的碟形封装半导体激光器作为激光光源,经准直系统准直后的平行光束垂直入射到柱面微透镜阵列LA1上,LA1将入射光分割成大量细光束,再经柱面微透镜阵列LA2和傅里叶透镜FL积分叠加后会聚在焦平面上,焦平面处放置CCD,使其靶面与焦平面重合,用于观察成像光场分布,其中,傅里叶透镜FL焦距大小fFL为133 mm。在本实验中,共有四片柱面微透镜阵列,具体参数如表1所示,选取不同参数的微透镜阵列组合组成了以下两个不同的实验系统:

实验一:柱面微透镜阵列1作为LA1,柱面微透镜阵列2作为LA2；

实验二:柱面微透镜阵列3作为LA1,柱面微透镜阵列4作为LA2。

图5 基于柱面微透镜阵列的光束匀化系统实验装置Fig.5 The experimental device of beam homogenization system based on cylindrical microlens array

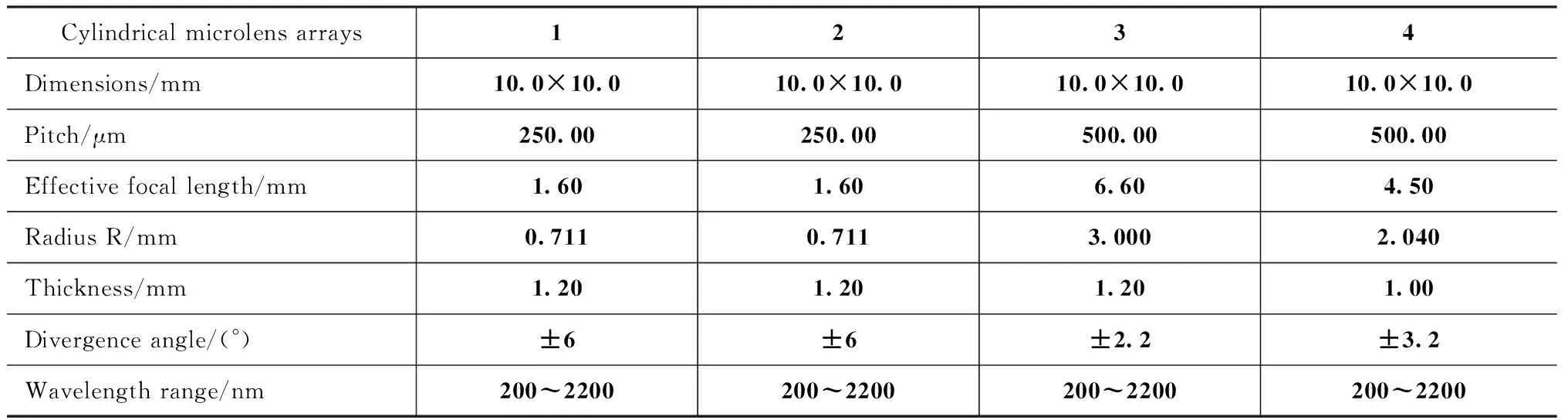
表1 柱面微透镜阵列匀束实验系统参数Tab.1 Parameters of cylindrical microlens arrays experiment

3.2 实验结果

3.2.1光束均匀性与微透镜阵列参数的关系

分别搭建实验一与实验二,通过CCD探测焦平面上的成像光斑,当两组实验中微透镜阵列间距为第一列微透镜阵列的焦距时,所测图像如图6所示,其中图6(a)为实验一成像光斑图像,图6(b)为实验一光强分布图；图6(c)为实验二成像光斑图像,图6(d)为实验二光强分布图。从图中可以看出,两组实验均实现了高斯光束的平顶匀化,目标平面上的光束呈均匀的矩形线光斑,光斑表面光强均呈现出明暗相间的条纹分布,这主要是由于入射光束经由微透镜阵列中多个孔径大小相同的子透镜分束后成像,而子透镜是紧密排列的,这种周期分布的结构很容易造成多光束的干涉,从而在像面产生大量干涉条纹,而光斑边缘轮廓出现凸起主要是由于单个子透镜的衍射作用造成的,上述结果与仿真结果相一致。

对比两组实验结果,可以看出实验二光束均匀性明显优于实验一光束均匀性,这主要是因为实验一所用微透镜阵列子透镜孔径为250 μm,实验二所用微透镜阵列子透镜孔径为500 μm,子透镜孔径越小,光源所分子束越多,当各部光波再次相遇时,子束越多相干叠加越强烈,使得光场干涉条纹更加明显,造成实验一光斑均匀度小于实二光斑均匀度。该结果与仿真结果一致,证明子透镜孔径越大,成像光场分布更加趋于平顶分布,光束匀化效果越好。

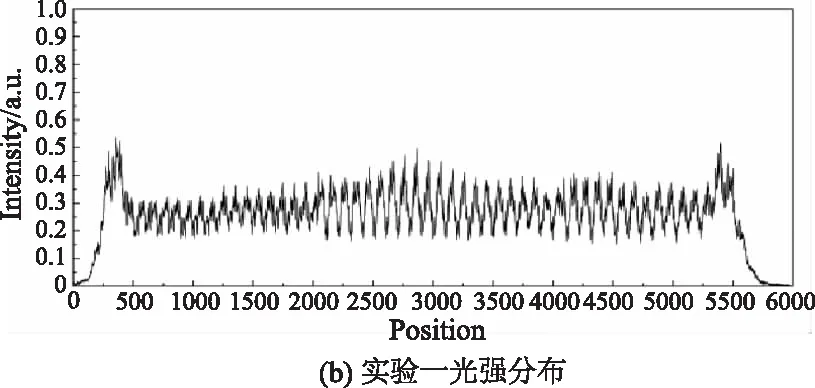
图6 目标面成像光斑Fig.6 Imaging spot of target plane

3.2.2 微透镜阵列间距对光斑长度的影响

调节微透镜整列LA1与LA2之间的距离d,用CCD观测不同微透镜间距时傅里叶透镜焦平面上的光斑长度大小,记录下相应的数据。图7为实验测量结果,其中图7(a)为实验一实验结果,图7(b)为实验一理论计算结果,图7(c)为实验二实验结果,图7(d)为实验二理论计算结果。

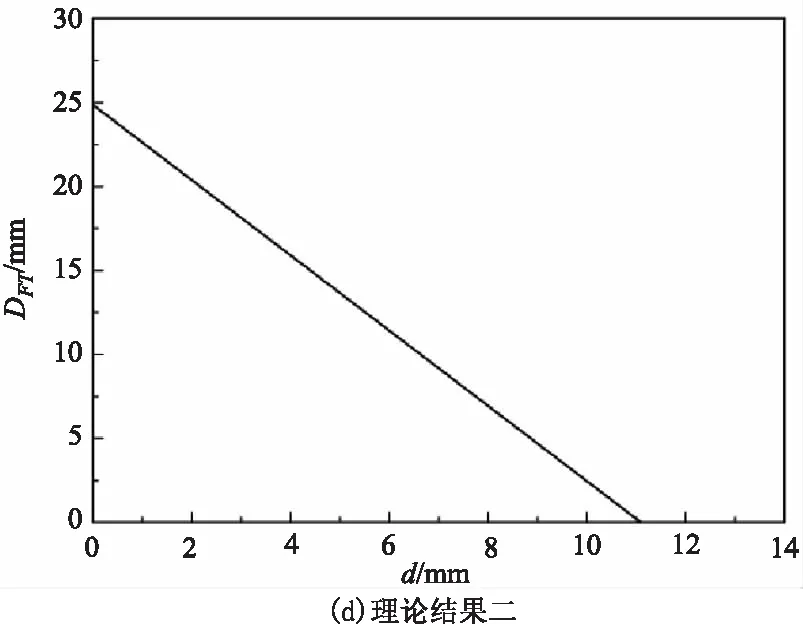
图7 光斑长度与微透镜阵列间距的关系Fig.7 The relationship between spot length and microlens array spacing

在实验一中,目标平面上的光斑长度随着微透镜阵列间距的增大呈线性减小,光斑长度在5～34 mm范围内可调,当微透镜阵列间隔最为实验所能调节的最小距离0.5 mm时,光斑长度可以达到最大34 mm,当微透镜阵列间隔为3 mm时,光斑长度降至最小5 mm,大于该距离后,光斑长度不再发生改变,实验结果理论具有一致性。在实验二中,焦平面上的光斑长度随着微透镜阵列间隔的增大呈线性减小,光斑长度在2～24 mm范围内可调,当微透镜阵列间隔最为实验所能调节的最小距离0.5 mm时,光斑长度可达到最大24 mm,当微透镜阵列间隔调至11 mm时,光斑长度降至最小2 mm,大于该距离后,光斑长度不再发生改变,实验结果与理论具有一致性。以上实验结果表明,该系统能够实现准直高斯光束的平顶匀化,得到长度可调的矩形线光斑,光斑长度与微透镜阵列间距呈线性正相关。

4 总 结

本文设计了一种基于柱面微透镜阵列的成像型光束匀化系统,基于矩阵光学理论,对系统进行了光线追迹,分析了靶面光斑长度的影响因素,基于傅里叶光学理论,建立了系统数学模型,通过MATLAB数值求解,仿真分析了成像光场光强分布特性。最终,通过搭建实验系统,实现了高斯光束的平顶匀化,获得了均匀的线光斑,改变微透镜阵列间距可以实现线光斑长度的灵活调节,长度在2～34 mm范围内可调,该结果与仿真结果相吻合。