一种多模式融合的激光点云配准算法

彭 蹦,杨耀权,江鹏宇

(华北电力大学控制与计算机工程学院,河北 保定 071003)

1 引 言

自20世纪60年代以来,三维空间信息技术(spatial information technology,SIT)不断发展,三维激光扫描(terrestrial laser scanning,TLS)作为SIT主流技术,广泛应用于工程测量、军事技术、数字城市模型、历史文物保护等领域[1],数字信息数据采集的逆向工程技术在三维重建中的作用也越发明显[2]。然而,TLS技术在实际工程应用中,往往需要多站点、多角度扫描才能得到完整的目标三维表面信息。因此,在同一坐标系下,片段式点云数据的精准整合,在三维重建领域内尤为重要,点云配准精度指标也会直接影响到三维模型的后期数据处理工作。

目前,国内外主流的点云配准算法均是在Besl和Makay提出的传统ICP[3]基础上加以改进的算法,摆脱了传统ICP算法收敛速度慢、点云配准误差大以及配准效率低的问题,改善了点云的配准效果。

从点集特征关系出发,杨小青[4]等人提出基于法向量特征的改进配准方法；陶海跻[5]等人根据局部法向量特征的变换提取配准特征点；郎萍[6]等人提出基于旋转图像特征描述子的方法；Bhoram Lee[7]等人提出学习各向异性ICP(LA-ICP)算法,从对象深度数据流中将不确定参数化成不同方向下的高斯算子；李仁忠[8]等人在传统ICP配准算法的基础上,提出使用内部形态描述子(ISS)特征点的方法,对点云进行精确配准。针对目标函数及搜索域设定,Mouna Attia[9]等人从三维点云初始状态角度出发,对ICP算法目标函数进行高效猜测；杨军[10]等人提出了一种基于自适应最优阈值的ICP改进算法,解决整体与部分3D模型间的配准问题；张名芳[11]等人提出在线学习合并阈值的层次聚类算法,结合点云的空间密度分布改善目标函数聚类结果。针对尺度变换矩阵,赵夫群[12]等人提出基于有界旋转角的改进ICP配准方法；付怡然[13]提出一种基于Gauss-Newton来改进非线性最小二乘法的算法,对尺度变换矩阵进行精准求解,并结合正态分布变换(normal distribution transform,NDT)最终实现点云的精细配准；蒋悦[14]等人提出一种高维正交子空间映射下的尺度点云配准算法,解决了无序、数据被遮挡且噪声干扰较大的点云配准问题。

上述方法对传统ICP配准算法的改进停留在收敛速度或点云配准精度上,两者兼顾性不强,尤其当激光点云数据量较为庞大时,以上改进的算法在点云配准效率上不是十分理想。

本文将源点云和目标点云按区域层次进行粗略划分,形成两大类区域方格,依据每个方格所在区域的法向量夹角特征,寻求点面曲率对应关系,完成点云的初始配准；在此基础上,估算尺度变换矩阵的边界旋转角度,结合相关系数迭代因子,对刚性变换参数进行最优化调整。通过仿真实验验证,针对20000数据点以上的点云,本文算法能明显有效地提高点云的配准精度,提升算法收敛速度。

2 点云预处理

依据传统ICP 配准算法的结构,大体可分为五个步骤:选择特征点对集、确定目标搜索函数、设定约束条件和策略、剔除无效点对、求解刚性变换矩阵参数。本文点云预处理过程包括有特征点对集的选择和目标搜索函数的确定。其中,主要从点云区域划分、法向量夹角特征点选择以及曲面曲率对应关系三个方面来进行说明。

2.1 划分点云格

将待配准的A*、B*两组原始点云数据分别进行随机均匀采样,并以各个采样点为初始聚类中心,随后利用基于欧氏空间距离的C—均值聚类法进行多次类聚,将点云数据划分为若干单元格子。欧氏空间距离公式如下:

(1)

其中,a和b分别表示空间n维向量；d12表示欧式距离。

2.2 提取法向量关键点

法向量夹角特征会随着点云区域的起伏发生改变,如图1所示。

图1 不同点云分布区域的法向量Fig.1 Normal vector of different point cloud distribution areas

其中,γ2为平缓区域法向量n2的法向量夹角；γi+3为曲面区域法向量ni+3的法向量夹角；nx表示点云区域点的法向量,其中x=1,2…,i+j。

可以看出,在同一坐标系内,点云平缓区域法向量夹角特征变化缓慢；而在点云曲面位置区域,法向量夹角特征变化快速,两者特征区分比较明显。

此时,引入特征度概念,即点云分布区域某点ak的法向量夹角变化程度。同时可知,fi为点云法向量和其k-邻域点法向量夹角的算术平均值。

(2)

其中,θij是γi法向量和γj法向量的夹角。

结合特征度的定义,在源点云集A*、B*中提取点云法向量特征关键点,形成点云初始配准点对集。其中,点云平缓区域在配准过程中精度高,尺度迭代变换形态固定,而点云曲面区域在配准的过程中容易发生错误,从提高曲面区域点云配准精度的角度出发,应选择fi大的点作为特征点,使曲面区域分布有比较多的法向量夹角特征。法向量特征关键点提取步骤如下:

1)设定关键点提取阈值δa,若某点处的法向量夹角算术平均值fi≤δa,则说明该点处在点云平缓区域,特征价值不高,应舍去；若某点处的法向量夹角算术平均值fi>δa,则说明该点处在点云的曲面区域,记录该点三维信息,予以保留；

2)判别fi是否满足在k-领域点内取得最大值max,如不满足,则继续在k-领域点内寻找,fi最大值点即为关键点am；

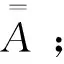
2.3 选取初始匹配点对

曲率关系是三维曲面特征变化的一种表现形式,而刚性变换对曲率关系影响较小,因此曲率可以作为点云特征匹配的一个重要指标形式。

本文主要以曲面的平均曲率关系作为初始特征点对匹配的依据,设曲面S中某一点M处的平均曲率为Kn,其中,曲面S的表达形式如下:

z(x,y)=Ax2+By2+Cxy+Dx+Ey+F(3)

式(3)中各系数可以用一、二阶导数表示:

(4)

(5)

(6)

(7)

(8)

可知,平均曲率Kn满足公式:

(9)

U={(a1,b1),(a2,b2),…,(ai,bi)}

(10)

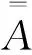
3 点云精确配准

仅根据点间平均曲率关系进行特征点粗匹配容易产生多种匹配点对结果,从而导致较大的配准误差,因此在粗匹配基础上通常需要增加点间距离约束条件,剔除错误匹配点对[15]。再依据边界旋转角约束旋转矩阵及位移矢量,使用动态迭代相关系数优化刚性变换参数,最终完成点云的精确配准。

3.1 点间距离约束

在集U中任意取两组点对(ai,bi)和(aj,bj),考虑到离散点云间一般无法完美匹配,因此通常取某一小的正临界阈值点δb,满足下式:

(11)

式中,dist( )表示欧式点间距离函数。

点云在坐标尺度变换后,曲率关系相似点对之间的距离关系会维持在固定比例区间,依据这一特征,可以判定点对(ai,bi)和(aj,bj)是否符合点间距离比值约束条件,若符合则保留匹配点对；否则,剔除错误点对关系,粗略对齐源点云和目标点云的数据特征点。

3.2 边界旋转角

绕任意轴的三维旋转可分解成单独绕X、Y、Z单坐标轴旋转的叠加,若假定旋转角分别为θx、θy、θz,则有如下旋转矩阵关系:

(12)

(13)

(14)

分别求解X、Y、Z三个轴方向上的平均旋转角度,记作Ex、Ey、Ez；估算X、Y、Z轴方向边界偏差旋转角,分别记作Δθx、Δθy、Δθz。将旋转角的上、下边界约束刚性变换矩阵,可得:

(15)

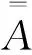
3.3 改进ICP算法

综合上述理论分析,本文基于法向量和边界旋转角融合的改进ICP算法流程如图2所示。

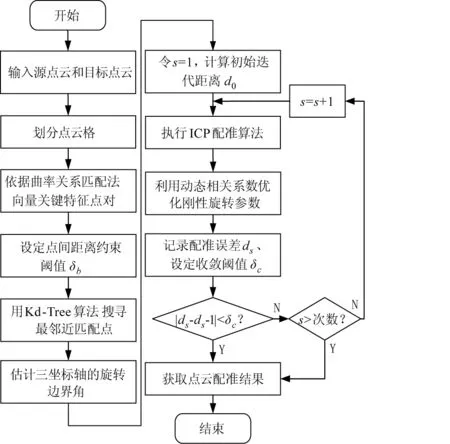
图2 改进ICP算法流程图Fig.2 Improved ICP algorithm flow chart

算法大体步骤可描述为:

1)将利用点间约束条件匹配得到的精确点对作为初始状态,开始进行迭代运算,令s=1；

2)估计三个坐标轴方向的旋转角边界值,其中X轴旋转边界值[Ex-Δθx,Ex+Δθx],Y轴旋转边界值[Ey-Δθy,Ey+Δθy],Z轴旋转边界值[Ez-Δθz,Ez+Δθz]；

(16)

4)通过相关性{i,ds+1(i)},建立动态迭代相关系数gs∈{1,2,3,…,ND},优化刚性旋转变换参数Rs和ts；

(17)

(18)

6)若|ds-ds-1|小于迭代收敛阈值δc或者大于算法预设的最大迭代次数,则停止迭代运算；否则令s=s+1,返回第三步,直到满足循环跳出条件为止。

4 实验结果与分析

本文基于Windows 10 64位操作系统,结合MATLAB R2015b完成三维点云模型的配准仿真实验。为验证本文算法的改进效果,实验过程将传统ICP算法、文献[4]提出的基于法向量改进ICP算法和本文算法三种仿真实验结果进行类比研究。

仿真实验分别从斯坦福大学计算机图形学实验室的开放数据中,提取兔子点云RabbitBunny00、RabbitBunny45和椅子点云Chair01、Chair02做实验数据。其中,设定参数值:曲率搜索误差阈值为du=0.003,法向量夹角特征提取阈值δa=0.005,点间距离约束条件下的阈值δb=0.002,算法收敛阈值δc=0.005,迭代次数达60次跳出迭代循环。

在兔子点云中提取法向量夹角特征,结合点面曲率对应关系完成点云的初始配准,如图3所示。

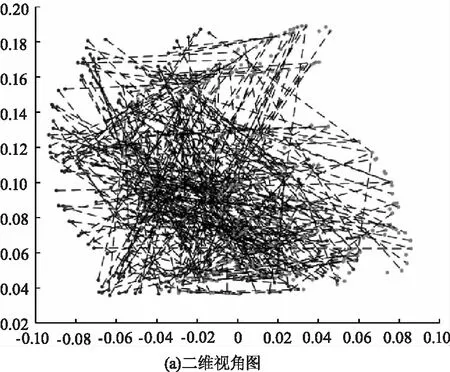
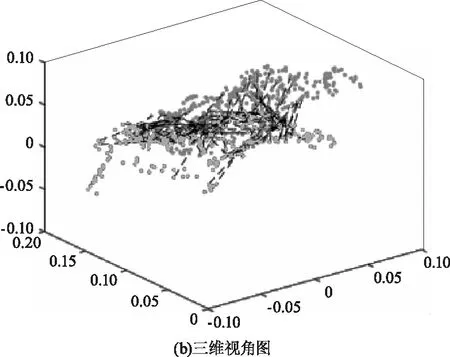
图3 法向量夹角特征点匹配Fig.3 Normal vector angle feature point matching

在点间距离约束条件下对初始匹配点对进一步约束,形成二次再匹配点对集结果,如图4所示。

图4 点间距离约束下的匹配点对Fig.4 Matching point pairs under the distance constraint between points

估算尺度变换矩阵旋转角的边界值,开始运行ICP算法迭代循环,分别得到传统ICP算法、文献[4]提出的基于法向量改进ICP算法以及本文改进ICP算法的三条迭代误差曲线,如图5所示。

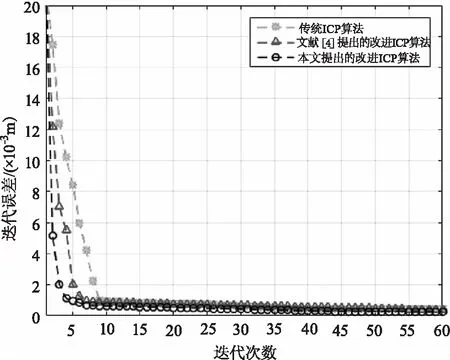
图5 三种算法的迭代误差曲线Fig.5 Iterative error curves of the three algorithms

可知,本文改进的ICP算法迭代收敛速度最快、误差最小。针对不同规模下的点云数据,讨论算法的点云配准速度,三种ICP配准算法所耗费的时间如表1所示。

表1 不同ICP算法下的三维点云配准时间Tab.1 3D point cloud registration time under different ICP algorithms

通过表1数据可知,本文改进ICP配准算法与传统ICP算法相比,点云配准时间减少50 %以上,点云配准速度显著提升。但与文献[4]提出的改进ICP算法相比,本文算法在低数据量点云配准速率上存在些许不足。

依据MATLAB R2015b的仿真结果,从直观角度来分析点云配准的精度指标,兔子点云配准效果对比情况如图6所示。

针对Chair01和Chair02点云数据,参数设定值不变,依据MATLAB R2015b的仿真结果,得到Chair三维点云配准效果对比如图7所示。

可知,本文算法在点云的配准实现中,表现较好。从直观角度可以看出,本文算法相比于传统ICP算法和文献[4]提出的改进ICP算法,点云配准结果的重合度更高,迭代精度更大。其中,仿真误差结果以数据的具体形式如表2所示。

图6 兔子点云配准效果对比Fig.6 Comparison of rabbit point cloud registration effects

图7 椅子点云配准效果对比Fig.7 Comparison of the point cloud registration effect of the chair

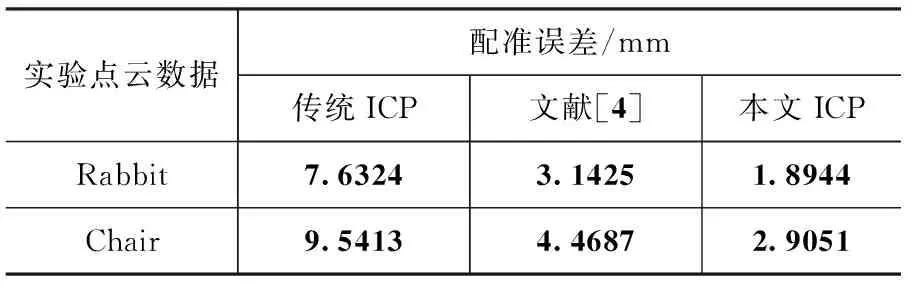
表2 不同ICP算法下的点云配准误差Tab.2 Point cloud registration error under different ICP algorithms

可得,本文改进的ICP算法针对上述两类实验点云数据,点云配准误差降至3 mm以下,在点云配准精度上大大优于传统ICP算法和文献[4]提出的改进ICP算法。

5 结束语

本文提出一种基于法向量特征和边界旋转角相结合的改进ICP配准算法,在点云区域层领域采用点云划分的方法,大大缩短大数据点云的配准时间。在点云配准过程中,首先搜寻点云格的法向量夹角特征,结合点面曲率对应关系,确定点云初始配准结果；随后人为估算尺度变换矩阵的旋转角度,结合相关迭代系数优化尺度变换参数,最终得到精确配准点云结果。

通过实验表明,本文改进算法在传统ICP算法的基础上,实现了对点云配准准确性和快速性的优化处理。对20000数据量以上的点云,相比传统ICP算法和文献[4]提出的算法,本文算法是一种更为有效、快速、准确的点云配准算法。