基于电压补偿的弹光调制器稳定性控制方法研究
2020-05-12王艳超张敏娟李克武王金伟刘文敬
王 楠,王艳超,张敏娟,李克武,王金伟,刘文敬
(1.中北大学信息与通信工程学院,山西 太原 030051;2.中北大学山西省光电信息与仪器工程技术研究中心,山西 太原 030051;3.山西省军区数据信息室,山西 太原 030051)
1 引 言
弹光调制器是由各向同性的弹光晶体(如硅、氟化锂、氟化钙、熔融石英、硒化锌晶体等)和压电石英晶体组成的热机电耦合器件,工作过程中,外部驱动电压信号输入到压电晶体,压电晶体发生振动,产生的应力作用于弹光晶体上,使得入射激光经偏振片后的线偏振光,通过弹光调制器产生相互垂直的两束偏振光,从而对入射光实现相位调制[1-3]。
弹光调制器稳定工作时,高压驱动器的输出电压幅值越高,弹光调制器产生的相位差越大,但是弹光调制器工作过程中由于机械振动产生的热损耗导致谐振频率发生漂移,导致驱动电路的输出频率与弹光调制器的谐振频率很难保持一致,干涉图产生的相位差也会随之减小,从而降低了弹光调制器的稳定性和调制效率[4]。Tudor N等人对导致弹光调制器工作不稳定的因素进行了解释分析,并设计了多PEM串接式谐振控制系统[5]。传统的弹光调制干涉仪,驱动能力不强,带负载能力弱,输出电压需要外接可调电源来进行调节,电压以及频率也需要信号发生器来调节[6-8]。本文采用的是基于FPGA的DDS技术控制PEM工作的方波信号,通过LabVIEW来实时调节频率与占空比控制字,进而实现对电压频率的调节。
针对弹光调制器谐振频率漂移问题,本文在建立弹光调制器的振动模型和频率温漂模型的基础上,提出了基于数字锁相技术的驱动电压自调节方法,该方法利用直接数字频率合成器技术(DDS),通过调节输出方波时钟信号的占空比来调节输出电压幅值,以使得弹光调制器在谐振状态下保持相位延迟量按正弦规律变化。
2 弹光调制器的频率温漂特性分析
弹光调制器的工作原理如图1所示,在弹光调制器中,外部驱动电压驱动压电材料(如压电陶瓷)产生应力.作用于各向同性的光学材料(如熔融石英)上使弹光晶体产生共振而形成周期性的弹光效应,因此入射光通过弹光调制器后其干涉信号的相位差被调制[9-14],可变相位延迟量为:
(1)
式(1)中,δ0为弹光调制器的调制幅值;f0为弹光调制器的谐振频率;k为弹光晶体的应力光学常数;Vm为驱动电压峰-峰值;d为弹光晶体的厚度;λ为入射光的波长;ω为简谐振动激励信号频率。
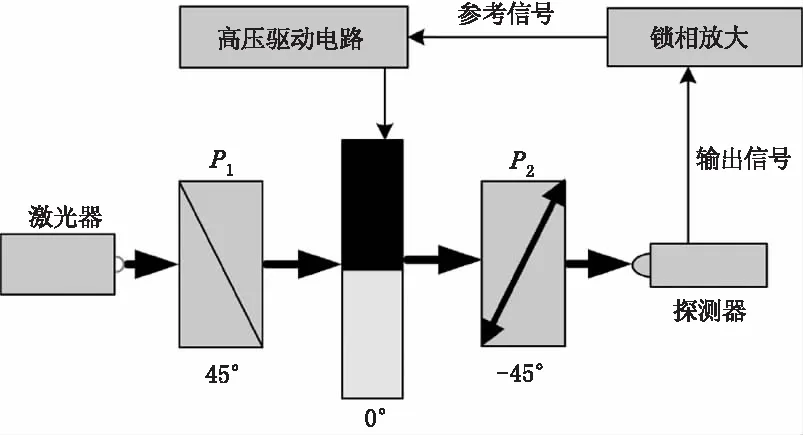
图1 PEM工作原理图Fig.1 The working principle diagram of the PEM
由式(1)可知,弹光晶体的厚度、应力光学常数以及入射光的波长确定时,弹光调制器在高压驱动下进行高频振荡过程中产生的热耗散、频率漂移比较严重,从而改变了弹光调制器的谐振频率,因此构建弹光调制热交换动态模型,因此我们构建弹光调制热交换动态模型,如图2所示。

图2 弹光调制器热交换动态模型Fig.2 Dynamic model of thermal exchange of elastic modulator
其中,V(t)为Tamb驱动电压;Z(ω)为弹光调制器等效阻抗,为环境温度;ω为驱动弹光调制器的高压交流信号的角频率;ωr为弹光调制器固有谐振频率;T为弹光调制器本身的温度。
对于弹光调制器在工作过程中产生的热耗散问题,我们将弹光调制器等效为LRC谐振动态模型,用电路的方式来进行解释,如图3所示。
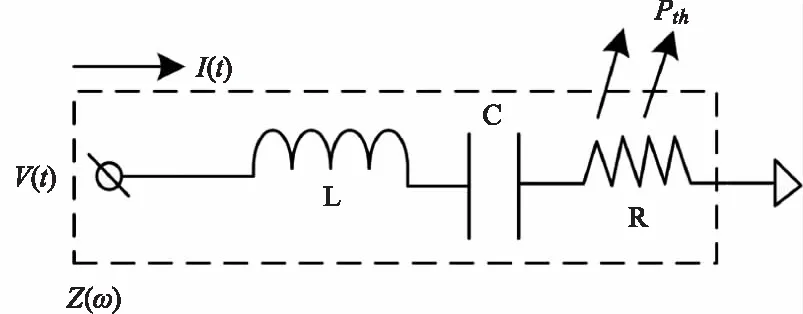
图3 弹光调制器谐振等效模型Fig.3 Resonance equivalent model of elastic modulator
其中,L为等效电感;C为等效电容;R为弹光调制器的等效阻抗。驱动信号V(t)施加在PEM上产生的热耗散与品质因数Q、谐振电抗Z(ω)和谐振频率ωr有关,得谐振电抗Z(ω)的表示:
(2)
由式(2)可得弹光调制器工作时产生的热耗散功率:
(3)
由上式可得ω=ωr时,PEM处于最佳谐振状态,产生的热耗散最大,因此产生的相位延迟量也最大,反之相位差减小[15]。
PEM工作中产生的热耗散一部分以热交换方式扩散到周围的环境中,另一部分导致弹光调制器自身温度升高[16-17]。
PEM与周围环境进行热交换,所引起的温度变化率为:

(4)
其中,τth=Rth·c为热时间常数;c为PEM比热容;Rth为PEM与环境温度之间的热阻抗[18];T为PEM自身的温度。
针对弹光调制器在高压激励下其谐振频率的漂移、品质因数降低,为保证弹光调制器工作于最佳谐振状态,将研究以数字锁相技术为核心的驱动电压自调节系统,以使弹光调制器产生稳定的相位差。
3 基于FPGA的数字锁相
入射激光经45°起偏器后的Stokes参量为:
(5)
其中,I0为入射激光经起偏器后的光强。
PEM的Muller矩阵[19-21]为:
(6)
检偏器P2的Muller矩阵为:
(7)
入射光经过图1所示光路系统后,得出射偏振光的Stokes参量[22]为:
Sout=MP2MPEMSin
(8)
将式(5)、(6)、(7)代入式(8)得探测器探测到的光信号[23-24]:
(9)
探测器接收到的信号为:
(10)
将cos(δ0sinωt)用第一类贝塞尔级数展开得:
(11)
其中,k为正整数;J0为0阶贝塞尔级数;J2k分别为2k阶贝塞尔级数。
将式(11)代入式(10)得探测器的输出为:
(12)
式中,K为光电常数,与光电探测器转换系数和放大器增益有关。由式(12)可知,探测器输出信号包括直流和偶次倍频项。实验中主要是保证四倍频项与二倍频项的比值稳定进而使PEM干涉信号相位差保持稳定,所以基于数字锁相技术提取其二倍频和四倍频项。
表达式分别为:
V2f=-KI0J2(δ0)
(13)
V4f=-KI0J4(δ0)
(14)
两式作比可得:
(15)
由上式可得,PEM相位调制幅值δ0和四倍频与二倍频的比值的关系。因此通过比较相邻两次四倍频与二倍频的比值来调节输出信号的占空比控制字进而调节驱动电压幅值,使弹光调制器处于稳定。
4 驱动电压自调节系统的设计
为了使弹光调制器工作过程中始终处于稳定状态且产生的相位延迟量按正弦规律变化,首先将PEM调至谐振状态,但是工作一段时间后,PEM谐振频率会产生漂移,PEM不再处于谐振状态。为了保证PEM工作的稳定性,设计了基于数字锁相技术的驱动电压自调节方法,如图4所示。

图4 驱动电压自调节方法原理图Fig.4 The chart of the driving voltage self-regulating system
如图5所示为驱动电压自调节方法的具体实现过程:接通电源,基于FPGA的DDS模块产生一个频率、占空比固定的方波信号为高压驱动器提供时钟信号,同时产生的高压信号驱动PEM工作,入射光经弹光调制器调制后被探测器接收完成光信号转换为电信号,再经AD采样模块将数字信号传入FPGA中,与存储器中的二次、四倍频正弦参考信号以及二次、四倍频余弦参考信号分别进行乘累加运算,再进行平方和开根号得到四倍频与二倍频的电压幅值。最后将计算结果通过uart串口模块发送到上位机中的LabVIEW中,基于LabVIEW程序比较相邻两周期四倍频与二倍频的比值来实时调节占空比控制字,当下一周期得到的比值小于上一周期的比值,增加占空比控制字,反之,减小占空比控制字,从而使相位延迟量按正弦规律变化。
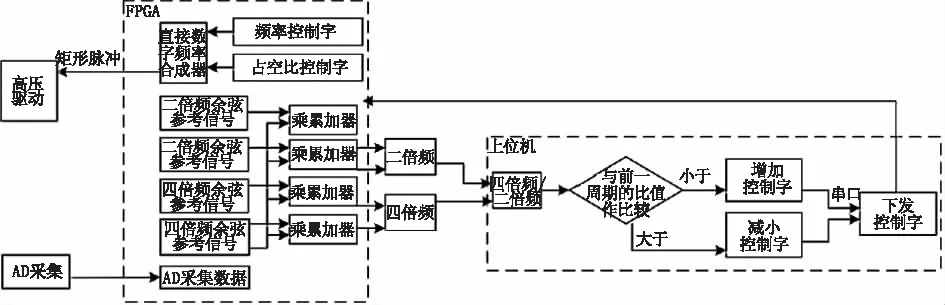
图5 驱动电压自调节控制过程Fig.5 Drive voltage self-regulation control process
5 实验验证与数据分析
实验系统包括光学系统、弹光调制器驱动电路、FPGA数字锁相电路、电源电路四部分,按照图6搭建了实验系统,起偏器和检偏器都采用Thorlabs公司的格兰泰勒偏振棱镜GT10,消光比优于105∶1,起偏器与x轴方向成45°,检偏器与x轴方向成-45°;PEM为山西省光电信息与仪器工程技术研究中心自行研制,其是具有双压电石英驱动的八角对称状结构的的硒化锌晶体,谐振频率为50.284 kHz;激光光源选用入射波长为632.8 nm的He-Ne激光器。

图6 弹光调制器稳定性系统实物图Fig.6 Physical diagram of the elastic modulator stability system
本系统实验测试使用的是泰克公司生产的四通道500 MHz带宽的DPO3054示波器,该示波器精度高,测量精确。测试仪器满足测试要求,具体测试过程如下:用Verilog语言编写DDS方波时钟信号发生程序使输出频率为50.284 kHz,编译链接成功后使用JTAG方式将程序下载到FPGA中,把高压驱动器的输出信号连接到示波器的一通道,DDS输出方波信号连接到数字示波器的二通道,然后手动调节占空比,首先通过数字示波器观察占空比为0 %时的驱动电压峰-峰值,然后占空比每隔5 %记录一次驱动电压峰峰值直到占空比为50 %,得出驱动电压随占空比的变化规律曲线,如图7所示。

图7 DDS方波占空比与驱动电压的关系图Fig.7 DDS square wave duty cycle and drive voltage
由图7可知,占空比在40 %~50 %之间电压基本保持不变,在50 %时电压峰-峰值达到最大值156 V。
如图8所示,通道1为高压驱动电路输出的电压峰-峰值,通道2为DDS输出占空比为50 %的方波、通道3为探测器接收的信号。

图8 方波占空比为50 %时的输出电压和经光弹调制后的信号Fig.8 Output voltage and photoelastic modulated signal when the square wave duty cycle is 50 %
如图9所示中两条曲线分别表示1 h内,驱动电压一定时的相位延迟量随时间的变化曲线以及带驱动电压自调节系统下的相位延迟量随时间的变化曲线,系统上电后首先调节PEM处于谐振状态,进而调节弹光调制干涉信号的四倍频与二倍频的比值在标准相位延迟量的附近,然后每隔5 min记录一次变化后的比值,记录1 h后发现比值逐渐减小,根据相位延迟量与比值的关系计算可得相位延迟量下降了15.6 %,针对以上情况,在PEM工作过程中基于LabVIEW程序比较相邻两次四倍频与二倍频的比值,运用DDS技术自动调节占空比改变驱动电压的幅值,仍然每隔5 min记录一次比值,记录1 h后发现比值变化幅度很小,经计算可得相位延迟量变化幅度为0.6 %,证明了驱动电压自调节系统的有效性。

图9 相位延迟量随时间变化Fig.9 Phase delay amount changes with time
6 总 结
本文针对弹光调制器工作时谐振频率漂移导致PEM干涉信号的相位延迟量减小的问题,建立了PEM热交换动态模型以及PEM的谐振等效模型,解释了温度对PEM的影响;提出了基于数字锁相技术的驱动电压自调节方法,并搭建了实验系统进行实验验证,实验结果表明:带驱动电压自调节时的相位延迟量变化幅度为0.6 %,电压一定时相位延迟量幅度下降了15.6 %,该方法提高了测量的准确度,使弹光调制器工作稳定。
