双频激光相干探测差频信号影响因素分析

任建迎,孙华燕,赵延仲,张来线

(1.航天工程大学研究生院,北京 101416；2.航天工程大学电子与光学工程系,北京 101416)

1 引 言

激光相干探测可实现对目标速度的精确测量,与直接探测相比具有测量精度高、灵敏度好、抗干扰能力强等诸多优点,研究人员针对激光相干探测技术开展了大量的研究工作[1-4]。但是在高速运动目标探测领域,由于目标的运动速度快,多普勒频移量大,受探测器带宽和数据采集系统的限制,现有的激光相干探测方法无法实现对高速运动目标的探测。

双频激光相干探测技术利用差频光实现高速运动目标的低多普勒频移量探测,大大降低了对系统设备参数的要求[5-7]。课题组提出了高速运动目标双频激光相干探测方法,采用单频光源分光技术实现双频激光的差频,利用差频光对高速运动目标进行探测,因为差频光的频率远低于光频,从而克服了低探测带宽和大多普勒频移的矛盾。作为探测信号的差频光直接影响系统探测的性能,因此分析差频光性能的影响因素对双频激光相干探测技术的应用至关重要。激光器是影响差频光性能的关键,对于平稳准单色光源,其频谱在频域内具有一定的频带宽度,即激光器线宽,在时间域内表现为有限长的相干长度或相干时间。激光线宽是衡量激光器性能的重要指标,根据经典干涉理论可知,相干场的条纹对比度、差频光的线宽与激光线宽有直接关系。李成强等研究了激光线宽对外差激光探测性能的影响,结果表明线宽的增加时影响中频信号提取精度[8]；陈明惠等研究了扫频激光瞬时线宽的影响因素,扫频激光的瞬时线宽随着色散的增加而变宽[9]；安颖等研究了超短时延的DFB激光器的动态线宽,提出了一种利用局部均值分解(LMD)的时频分析法测量激光动态线宽的方法[10]；陈长水等研究了差频法产生中红外光源的方法,结果表明输出光源线宽与抽运光和信号的线宽有关[11]。以上研究充分说明光源线宽对相干探测的重要影响,但对于双频激光相干探测的差频光影响没有具体分析,因此通过理论分析线宽对差频光的性能影响,对双频激光相干探测技术的应用具有重要意义。

本文根据双频激光相干探测高速运动目标的原理,结合随机过程理论分析了差频光的影响因素。通过维纳-辛钦定理得到了差频光的功率谱公式,根据此公式分析了激光线宽、振幅比对差频信号功率谱、信噪比的影响。讨论了差频光的条纹对比度与线宽和光程差的关系。

2 双频激光相干探测技术理论

双频激光相干探测技术通过双频激光相干产生的差频光探测运动目标,经目标反射后的回波光与参考差频光混频,得到低多普勒频移信号,经过滤波降噪处理提取目标的速度和距离信息。双频激光相干探测技术中差频光的产生方法主要包括:一是注入式锁模激光器的光学混频法[12-13]；二是单频光分束后将其中一路移频,然后将两束光合束混频[14]。

在双频激光相干探测中,拍频光的频率噪声和相位噪声与激光器输出信号的线宽、强度稳定性有直接关系。基于单光源分束移频法的双频激光相干探测系统如图1所示,激光器发射光源经过分束镜等比例分束,分束后的光场强度时域特性可表示为:

图1 双频激光相干探测原理框图Fig.1 Principle block diagram of dual frequency laser coherent detection

E1=E0(1+a(t))cos[2πft+φ1(t)]

(1)

其中,E0表示光场振幅;φ1(t)表示光场的随机相位;a(t)表示光源强度的随机波动,反应的是激光器强度噪声的大小,本文主要分析光源线宽对双频相干光的影响,因此忽略强度噪声的影响。另一光束经过移频器移频后的时域光场可表示为:

E2=ηE0cos[2π(f1+fIF)t+φ2(t)]

(2)

其中,η表示移频器的衍射效率,此处是影响差频信号振幅比的主要因素;φ2(t)表示移频后的光场随机相位;fIF表示移频量。移频后的光束与另一路光束通过耦合器混频,产生的差频光场强度的时域特性可表示为:

(3)

差频光经运动目标反射后的时域光场可表示为:

Es=αAcos[2π(fIF+δ)t+φs(t)]

(4)

其中,α表示回波光信号与参考光信号振幅比,0<α<1,δ=2VfIF/c表示目标运动引起的差频信号多普勒频移。由式(4)可知,探测高速运动的差频信号频率为fIF,频移量fIF一般在百兆赫兹到吉赫兹量级,属于微波波段。以1550 nm波长激光器为例,当频移量fIF=1GHz,目标运动速度为V=340 m/s时,双频激光相干探测技术多普勒频移为2.2667 kHz,而传统单频激光相干探测的多普勒频移为438.71 MHz,相比传统单频激光相干探测技术,双频激光相干探测技术多普勒频移量低了5个数量级,大大减小了对探测器、采集设备、数据处理设备性能的要求,可实现更高速度目标的探测。

3 差频信号功率谱分析

当激光光源服从广义平稳随机过程时,根据维纳-辛钦定理,可以通过差频信号自相关函数的傅里叶变换得到信号功率谱密度函数,差频信号的自相关函数可表示为:

=A2cos(2πfIFτ)×Re〈exp[-jΔφ(t,τ)]〉

(5)

其中,Re表示取函数的实部；〈〉表示求函数均值,Δφ(t)=φR(t+τ)-φR(t)表示不同时刻差频光相位的相关性,其服从零均值随机高斯分布。由上式可知,Re〈exp[-jΔφ(t,τ)]〉项是决定差频光线宽的关键量,即激光器的相位噪声是影响线宽的关键因素。根据理论关系式[15-16]:

〈eiΔφ(t,τ)〉=e-〈Δφ2(τ)〉/2

(6)

其中,〈Δφ2(τ)〉=2πΔf|τ|表示差频光随机相位的方差；Δf表示激光器的输出信号的半高全宽(full width at half maximum,FWHM),当时延τ非常小时,两光束是完全相干的[10],τc=1/πΔf表示激光光源的相干时间。则差频光场的自相关函数可表示为:

G(τ)=A2cos(2πfIFτ)e-πΔfτ

(7)

上式的傅里叶变换为差频光场的功率谱,体现的是差频光强的频域特性。差频信号功率谱函数可表示为:

(8)

由上式可知中心频率是fIF,功率谱分布受激光线宽Δf和振幅比的影响,差频信号功率谱函数表现为洛伦兹线型。移频量一定,且衍射效率固定的条件下不同激光线宽的差频信号功率谱分布如图2所示,由图可以看出随着光源线宽的增加,差频信号功率谱随之展宽,功率谱幅度下降。当移频量一定,且光源线宽固定时,不同衍射效率条件下的差频信号功率谱分布如图 3所示,衍射效率影响着两差频信号的振幅比,由图可得,当衍射效率越大功率谱幅度越大,此时的信号幅度越强。

差频信号信噪比计算可以采用频域积分的方法,认为功率谱峰值外的其他部分为噪声。信噪比计算公式:

(9)

差频信号的信噪比随光源线宽变化曲线如图 4所示,由图可得,随着光源线宽的增大信噪比随之下降。受移频器自身噪声、环境、衍射效率等多种因素的影响,频移量并不是一个严格固定的量,而是一个随时间起伏的变化量，移频扰动对功率谱的影响如图5所示。移频器的频率扰动量可以通过移频稳定度来衡量[17],移频稳定度可表示为:

(10)

其中,fn表示移频器的扰动频率；Δf表示移频器的中心频率。

图2 不同线宽的差频信号功率谱Fig.2 Power spectrum of different linewidth

图3 不同振幅比的差频信号功率谱分布Fig.3 Power spectrum distribution with different amplitude ratio

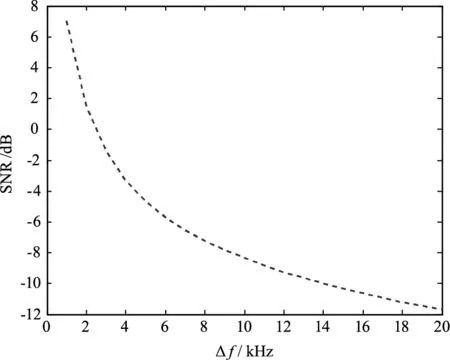
图4 差频信噪比随光源线宽变化曲线Fig.4 SNR curve with the linewidth of the light source

图5 移频扰动对差频光的影响Fig.5 The effect of frequency shift disturbance on differential frequency light

差频光的条纹对比度是衡量相干性能的重要参数,根据两光束在P点的合振动光强度分布为:

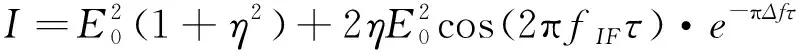
(11)

根据相干场某点的干涉条纹对比度定义[18],条纹条纹对比度可表示为:

(12)

Imax表示相干光场的最大值,当2πfIFτ=2nπ(n=0,1,2,…),差频光场强度取最大值:

(13)

Imin表示相干光场的最小值,当2πfIFτ=(2n+1)π(n=0,1,2,…)时,差频光场强度最小值:

(14)

差频光的条纹对比度可表示为:

(15)

(16)

式中,n是与延迟时间τ成正比的正整数,延迟时间越大n值越大,延迟时间是由两路光的光程差引起的。不同线宽的条纹对比度变化曲线如图 6所示,由图6可知随n的增加,差频光条纹对比度下降,且光源线宽越大下降速度越快,即光源线宽越大受光程差的影响越大。因此在双频激光相干探测中尽量保持合束前两路光的光程相等。不同衍射效率下的条纹对比度变化曲线如图 7所示,由图可以看出,在短延时下的条纹对比度主要受振幅比的影响,因此在生成差频信号中,尽可能的保证两路光的振幅比相等。

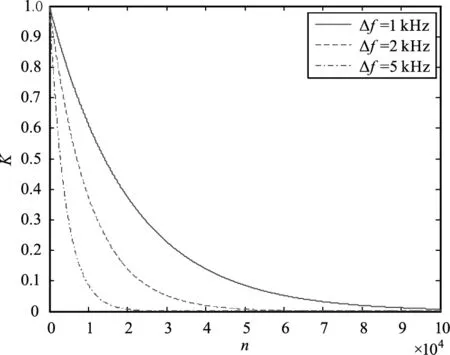
图6 不同线宽的条纹对比度变化曲线Fig.6 Variation curve of fringe contrast with different line widths

图7 不同振幅比下的差频光条纹对比度Fig.7 Contrast of light fringe with different amplitude ratio

4 差频光信号实验测试

实验过程中,采用532 nm单纵模激光器,最大输出功率200 mW,线宽<10-4nm,振幅稳定度<0.5 %,功率稳定性<1 %,相干长度>50 m。分束器的分束比为1:1；移频器采用Gooch&Housego AOMO 3080-125移频器,最大移频量80 MHz,衍射效率0.95,探测器距离合束镜头10 cm,避开的传输信道对差频光的影响。

探测器响应的差频光信号如图8所示,差频光的频率和幅度受到干扰,这是由于激光器、移频器不稳定造成的频率扰动和幅度起伏。差频光的频谱分布如图9所示,图9(a)和9(b)为不同时刻差频光的频谱,图9(a)的中心频率为69.13 MHz,3 dB线宽为760 kHz,图9(b)的中心频率为69 MHz,3 dB线宽为740 kHz。以上不同时刻差频光的中心频率的变化,证明了移频器存在移频量的扰动。差频光线宽的变化主要是由激光器瞬时线宽的变化引起的。

根据实验测试结果可知,由于激光器和移频器噪声的存在,差频光并不是严格的稳定信号,受移频器频率扰动的影响差频光的中心频率存在微小的变化,差频光的线宽受激光器瞬时变化影响存在起伏,频率扰动和强度起伏对差频光的影响在本文中不做描述。

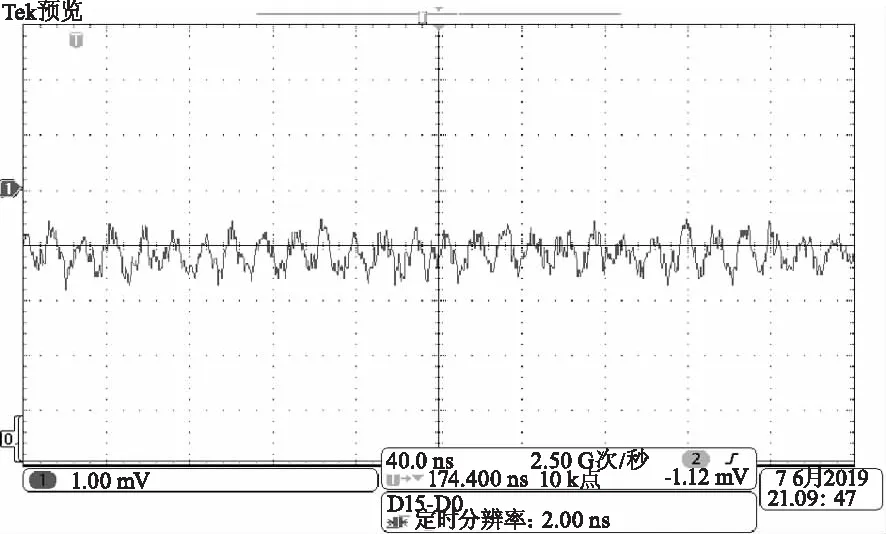
图8 探测器响应的差频光信号Fig.8 The difference frequency signal output by the detector

图9 不同时刻差频信号频谱及3dB线宽Fig.9 Different time difference frequency signal spectrum and 3dB line width

5 结 论

针对单频激光相干探测系统探测高速运动目标时的大多普勒频移与低探测带宽的问题,提出了单光源分束移频的双频相干探测方法,简单分析了双频激光相干探测的低多普勒频移的优势,介绍了差频光的产生方法。结合维纳辛钦定理得到了差频光的功率谱函数,重点研究了激光线宽、振幅比、光程差对差频光功率谱、信噪比、条纹对比度的影响。最后通过实验验证了差频光的产生方法,证明了激光器线宽、移频器频率扰动对差频光线宽和中心频率的影响。同时实验结果证明激光器、移频器等噪声对差频光振幅有一定影响,后续还需要深入的研究激光器和移频器噪声扰动对差频光的影响。