室内环境的数据融合自适应调控方法研究

庞维庆,何 宁,李秀梅,严 成

(桂林电子科技大学信息与通信学院,广西桂林 541004)

1 引言

室内环境污染已经成为全球公共健康的主要威胁,这需要在研究和政策制定领域付出更多的努力[1–3].据统计,大多数城市中的居民超过95%的时间处于封闭的室内环境中[4],而封闭空间中有害气体浓度达到一定值就可能对人体健康造成损害甚至危及生命,比如甲醛超标、一氧化碳中毒、粉尘污染等.因此,提供一个舒适的室内环境是一个提升健康、舒适度、生产力的关键因素[5].如何有效地对室内环境进行调控,为人们提供一个舒适、健康的生活、工作环境,是一个非常值得研究的课题[6].

室内环境是一种具有多变量、强耦合、不确定因素多、纯滞后、大惯性的参数时变系统.往往采用单一的数学模型难以准确描述,因而存在系统误差较大、耗能高、实时性和鲁棒性差等缺陷.针对这一领域目前存在的一些问题,国内外很多学者都进行了深入的探讨[7].Meana-Llori´an等人在考虑室外条件的情况下结合模糊逻辑和物联网技术对室内温度进行调控,该研究能够节省40%的能耗[8].刘运城提出一种运用Agent算法修改模糊规则,结合双线性控制算法提出一种新的智能建筑恒温控制模型,与传统算法相比能够大幅度提高控制系统的鲁棒性[9].以上研究以及文献[1,10–11]等均以室内温度动态调控为研究目标,仅仅考虑到室内温度对人体舒适度的影响,而没有涉及到室内空气质量的研究.Zhang等人综合利用窗户、风扇、空调等环境参数的适应控制方法能够将建筑综合征感染率降低到40%,并且能够节省31%到40%的能量[12],虽然节能效果显著,但是控制模型比较简单,精度较低.葛双等人在考虑室内温湿度、CO2浓度、照度等多种环境因素影响的基础上提出一种基于同策蒙特卡罗算法的控制器,能够较好地跟踪实际情况,误差较小,但是文中没有提及对各传感器数据的滤波与有效融合,在实际应用中还需要进一步改进[13].

由于室内环境体积较大,各参量调控输出具有很强的惯性和滞后性,如果采用传统的PID算法进行调控会引起超调过大,易起震荡,从而导致系统稳定性较差.针对以上最新研究成果中存在的不足,本文提出一种室内环境的数据融合自适应调控方法,在综合考虑室内空气质量、节能、环境舒适度的同时提高系统的智能化、自动化以及调节精度和抗干扰能力.

2 室内环境数据融合调控建模

2.1 多变量卡尔曼滤波模型

卡尔曼滤波器(Kalman filter)是基于最小均方误差准则的最佳线性滤波器[14],它能够从一系列的不完全及包含噪声的测量中,估计动态系统的状态.室内环境是一个缓慢变化的过程量,因而在足够短的信号采样时域T内,室内状态变化为一平稳随机过程,整个室内环境可看作一个离散时变线性MIMO系统[1].考虑到实际室内环境比较复杂,往往受到诸多因素的制约[8],本文选取室内环境质量的主要指标:二氧化碳(CO2)、温度(Temperature)、照度(Illuminance)、总挥发性有机化合物(total volatile organic compound,TVOC)进行研究[12,15–16].于是,室内环境状态可以表示为

根据室内环境状态变量的物理含义及其变化规律,得到以下各环境参量的状态转移关系

由此得到室内环境信号模型的状态方程

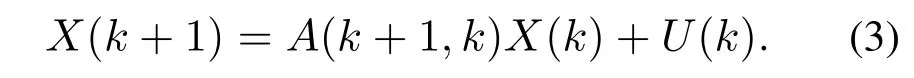
同理,CO2、温度、照度、TVOC对应的量测方程为

由此可以得到室内环境信号模型的量测方程

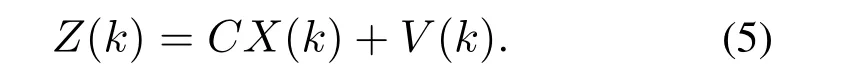
因为T足够短,故可以认为增益矩阵A,C不随时间变化,设U(k),V(k)都是均值为零的正态白噪声,方差分别为Qk和Rk,并且初始状态与U(k)和V(k)都不相关,γ表示相关系数,则有如下关系:

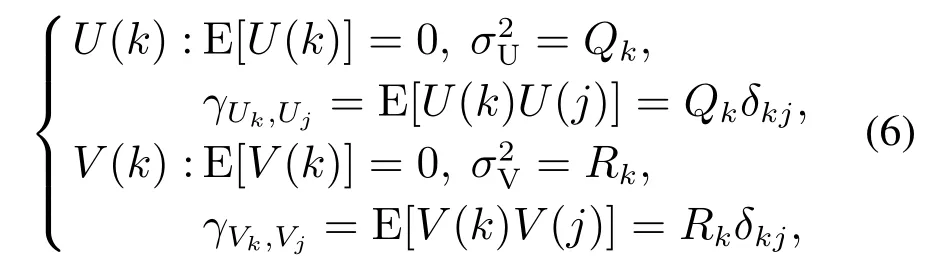
同理可以求出

由于X(k)真值不可知,故对传感器进行两次采样测量得到CO2浓度的两次测量值z1(1)和z1(2),温度的两次测量值z2(1)和z2(2),照度的两次测量值z3(1)和z3(2),以及TVOC的z4(1)和z4(2),从而可以由量测方程(5)得到状态变量的估计

每次测量信号的误差可以表示为

对于第2次测量数据,根据误差信号协方差矩阵P(k)的定义有

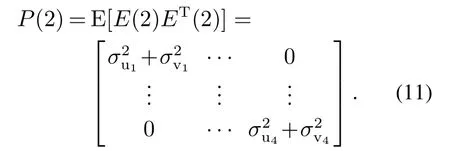
这样根据以上模型可以确定Q(k),R(k),,P(2),在给定初始增益矩阵H(k)时可以根据以下Kalman递推公式进行递推:

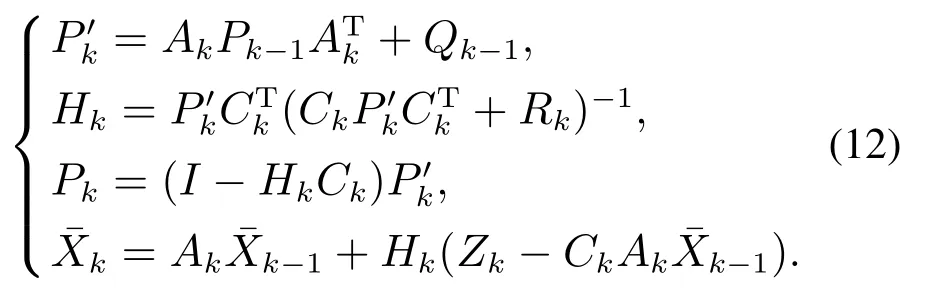
2.2 神经网络融合模型

多传感器测量得到的信号经过Kalman滤波模型处理之后,输入人工神经网络进行分析融合,并对当前各环境质量指标的控制期望值进行估计.BP神经网络(back propagation neural network,BP–NN)模型可以建立多维数据输入到多维数据输出之间的模糊映射,其数据融合过程可以分为两部分:信号的正向传播和误差的反向传播.一旦网络实际输出和期望输出之间存在偏差e,则该偏差沿着网络传输层返回,并调整神经元连接权值和阈值[17].

令模型的输入和输出分别为xi和ui,如图1所示.

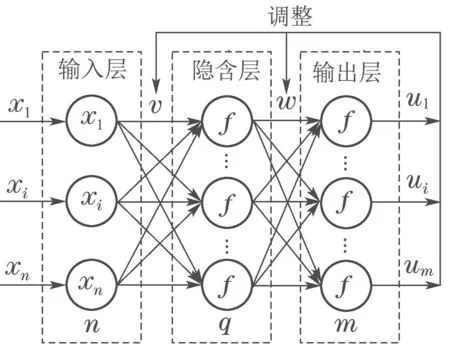
图1 神经网络模型拓扑结构图Fig.1 The topology structure of neural network

图1中:n为输入层神经元的传感器输入节点数,q表示隐含层神经元节点数,m为输出层神经元节点数,传输函数选择Sigmoid函数,其数学形式为

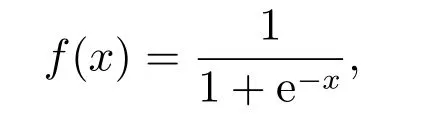
于是,隐含层第j个神经元输出可以表示为

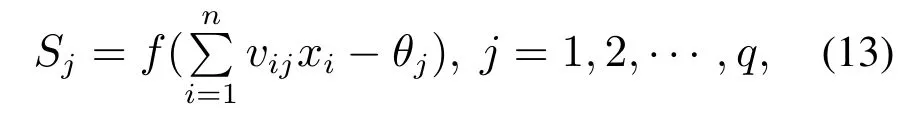
输出层第k个神经元的输出可以表示为

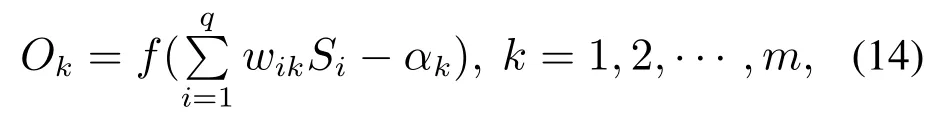
其中:θj,αk分别为隐含层和输出层的阈值,vij,wjk分别为隐含层和输出层的连接权重.d为期望输出,则第t个样本输出的均方误差为

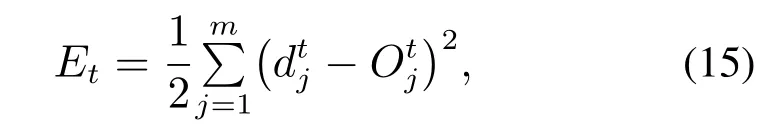
于是k个训练样本的总误差为

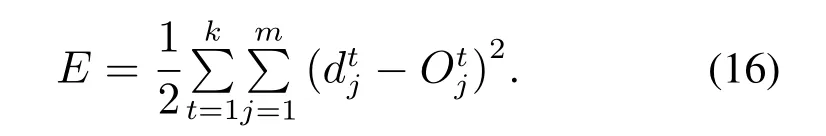
学习算法采用梯度下降法,可以得到

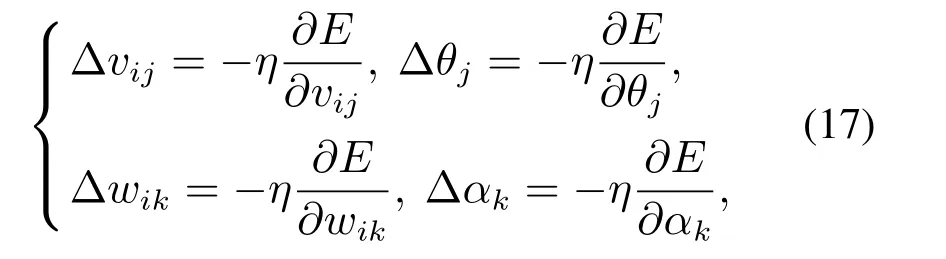
式中:∆vij,∆θj,∆wik,∆αk分别为输入层权值修正量、输入层阈值调整量、输出层权值修正量和输出层阈值修正量.

2.3 DMC控制模型

动态矩阵控制(dynamic matrix control,DMC)是一种基于阶跃响应的增量算法,在预测控制中使用较为广泛,稳定性好、鲁棒性强、能够克服系统的纯滞后或非最小相位特性,综合考虑比较适合室内环境的优化控制.DMC主要包括预测模型、滚动优化以及反馈校正3部分.

1)预测模型.

从k到k+i时刻对室内环境系统施加连续的M个控制增量∆u时,k+i时刻的输出估计为

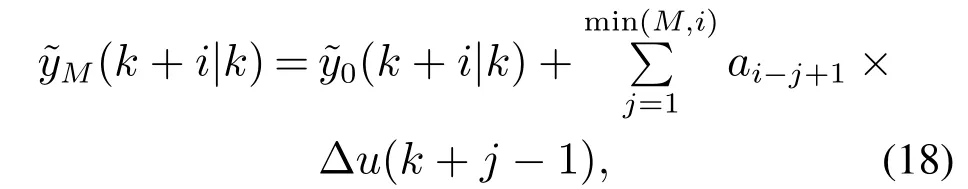
式中:i=1,···,N,为k时刻对k+1时刻的输出估计,N和M分别为建模和控制时域.

2)滚动优化.

控制过程中性能指标函数的范数形式如下:

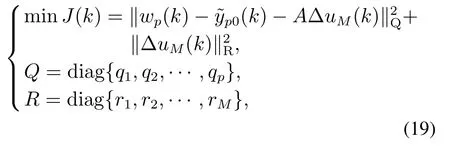
式中:wp(k)为系统在k时刻的输出期望,A为动态矩阵,Q为误差权矩阵,R为控制权矩阵.对性能函数求偏导,取极值时,有

式中:dT为控制向量,cT=[1 0···0]为取首运算.

3)反馈校正.

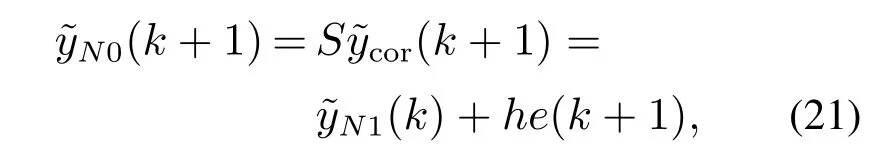
其中:e(k+1)为系统实际输出误差,移位矩阵

因而由预测模型式(18)可得到下一时刻的输出预测值

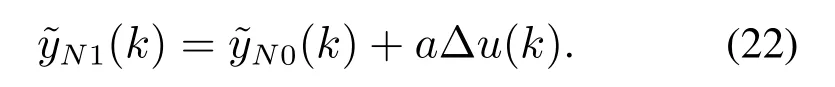
3 最优调控模型的数值求解

取定一个长度为T的信号采样时域,在该时域内对传感器进行N次采样,经过Kalman滤波器进行平滑滤波之后再进行后续的处理.神经网络分为3层:输入层、隐含层、输出层,其中各层神经元数量分别为4、6、4,输入输出变量分别对应CO2、温度、照度、TVOC.在系统运行之前,需要先对神经网络进行训练,依据室内环境国家标准(GBT18883和GB50325)以及文献[15]结合实际情况决定选取以下数据作为神经网络训练标准.

表1中,第1组数据为舒适值,第2组数据为最大值.先对以上期望数据细分为2000个区间,然后作为训练样本输入到网络模型进行训练.

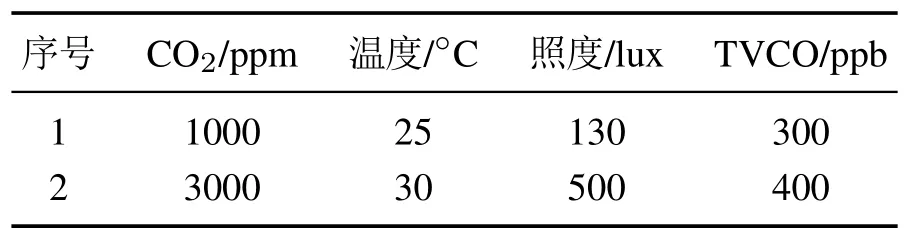
表1 室内环境质量标准值Table 1 Quality standard of indoor environment

图2–3给出了不同迭代次数的训练效果.实线表示网络输入,虚线表示输出期望,点线代表网络实际输出.由图可以看出,照度和温度值的输出期望应与网络输入无关,始终保持在预设的最优值附近;而对于CO2和TVOC等有害气体在输入浓度较小的时候,输出期望可随着输入的增大而增大,说明此时无需施加控制量,直到网络输入达到最大的期望值Vopt,这时候就需要施加控制量使得有害气体浓度稳定在Vopt附近,以避免对人体健康产生不利的影响.对比可以看出,训练次数为50次的时候,在前面的200个样本中CO2和TVOC浓度的网络实际输出跟期望输出差别较大,最大误差分别为160.47 ppm和24.59 ppb,随着样本数量的增加,在后面的训练集中表现则好一些;训练次数为2000次的时候,CO2和TVOC含量的网络实际输出与期望输出比较基本一致,拟合误差小于0.1773 ppb,效果较好,且网络输出能够稳定在Vopt以下,基本能够满足实际需要.

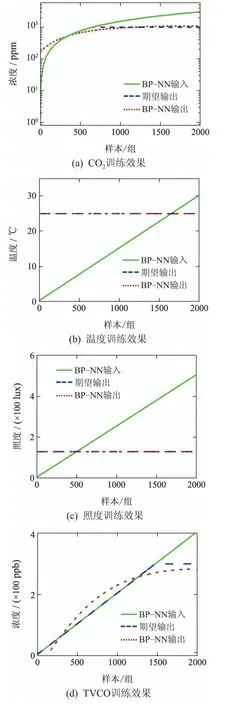
图2 迭代50次训练效果Fig.2 The training effect of 50 iterations

3.1 控制系统模型

控制系统模型结构如下图4所示,各状态变量的采样数据输入到Kalman滤波器进行滤波,得到当前状态的有效估计,然后输入到训练好的BP神经网络进行数据融合,从而得到当前状态的控制期望值,最后将状态估计值及其控制期望值输入到各参量对应的DMC控制器分别根据性能指标进行优化控制,从而达到优化调控的目的.

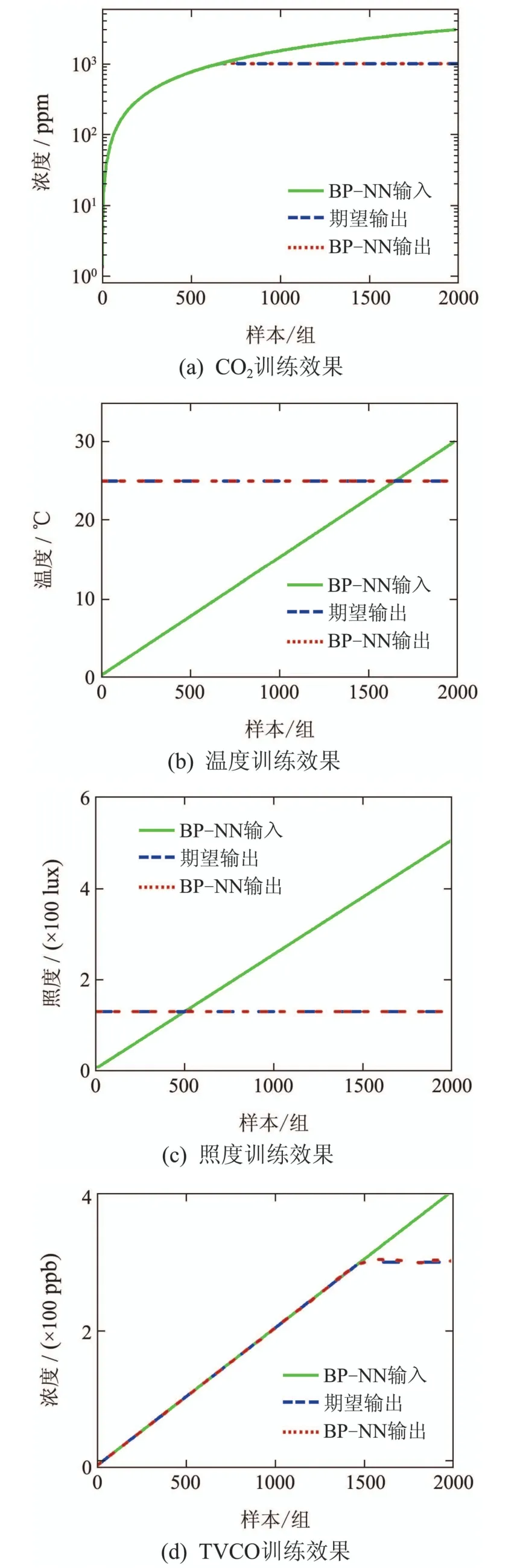
图3 迭代2000次训练效果Fig.3 The training effect of 2000 iterations

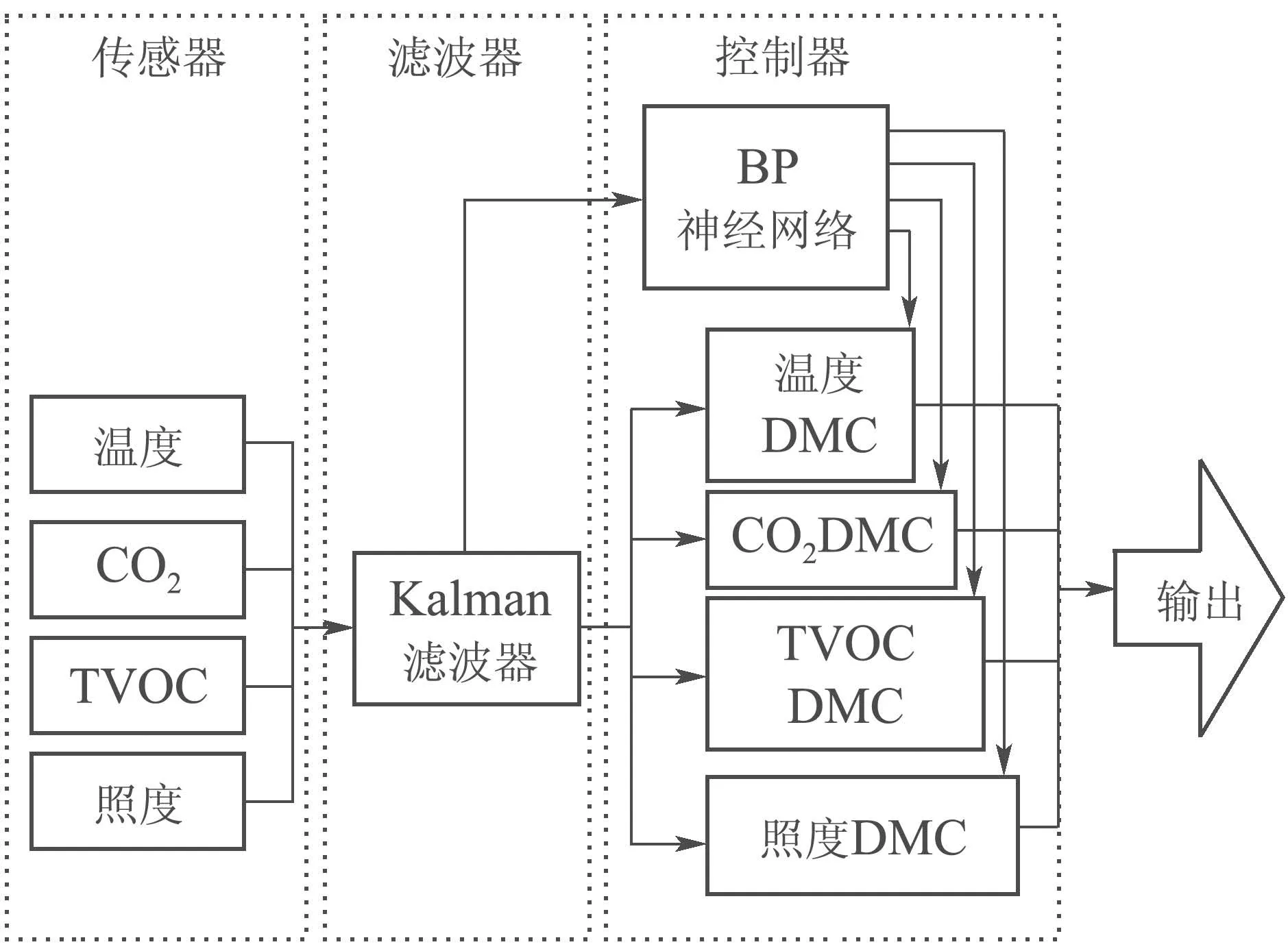
图4 室内环境控制系统结构图Fig.4 The structure of indoor environment control system

3.2 基本算法

步骤1参数初始化.先设定信号采样时域T以及采样次数N、初始Kalman增益H(k);确定DMC控制器的优化策略(即确定N,M,A,Q,R),并由式(20)计算dT;设定各环境参量的舒适值作为输出期望,并根据输出期望生成训练数据,确定神经网络参数(n,q,m,以及训练次数、收敛误差),然后对网络进行训练;

步骤2在信号采样时域T内对各传感器进行N次采样,得到室内环境当前的状态数据;

步骤3将步骤2中的数据输入Kalman滤波模型,按照式(1)–(11)计算Q(k),R(k),,P(2)并结合H(k)代入式(12)进行Kalman算法的迭代过程;

步骤4迭代过程结束,将步骤3中的滤波值输出到训练好的神经网络,对当前各状态变量的控制期望进行估计;

步骤5将步骤3中经过滤波的状态数据和步骤4中对应的控制期望值输入到DMC控制模型进行动态调控;

步骤6系统输出达到控制期望值,转向步骤2进行下一轮调控,否则继续步骤5.

4 系统实现及仿真结果分析

本实验中使用的数据采集硬件如图5所示.

图5 数据采集终端Fig.5 Data acquisition terminal

图6 数据汇聚节点Fig.6 Data aggregation node

为验证本文提出的数据融合自适应调控方法的正确性和有效性,并能够体现抗干扰性和节能优化原则,以某办公室冬季的环境数据为原型进行建模仿真.设定信号采样时域T为60 s,每隔1 s采集一次数据,总采样次数N为60次,部分数据如表2所示.

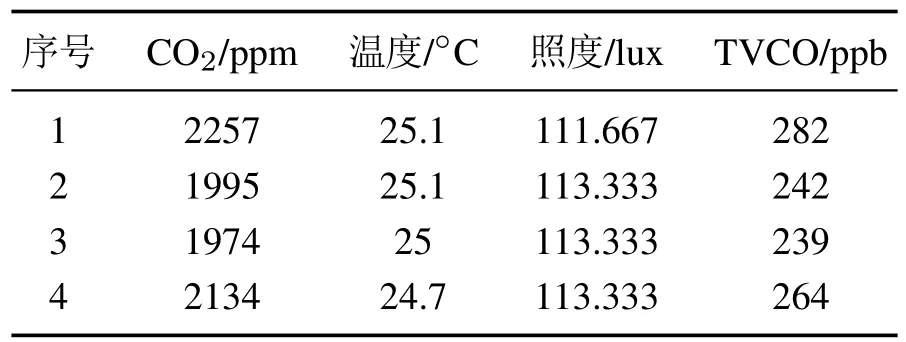
表2 部分采样数据Table 2 Partially sample data

对以上原始数据先进行简单的预处理,即根据表1的数据阈值范围去掉一些异常数据点,并从中选取前20组数据作为实验数据.图7中,表示从1到k时刻CO2量测数据的均值,从均值曲线可以看出,随着测量数据的增加,均值趋向于真值x(k)(由于真值不可知,严格来说,此处为真值的期望,即,实际应用中,往往涉及到多种不同传感器采集的大量数据,考虑到效率问题,N不可能取太大,因而造成一定的测量误差,图9显示了不同环境参量的均值滤波误差随样本数量的变化情况,可见,随着样本数的增加,均值误差趋于平稳且趋向于0.实验中,最终TVCO、照度的均值滤波误差较大,在3%左右,结果如表3所示.

表3 均值滤波结果Table 3 Result of mean filtering

4.1 Kalman滤波效果分析

初始Kalman增益H(k)设为0,取,状态噪声为高斯白噪声,由式(11)计算得到

代入滤波器根据式(12)进行Kalman迭代,限于篇幅,这里仅列出CO2浓度的滤波迭代过程,如图7所示,尽管量测数据z(k)由于随机噪声的干扰而出现较大的波动,状态估计在前面少量的几组数据中能够快速的收敛,并且根据最小均方误差准则不断地动态调整Kalman增益H(k)从而使得¯x(k)越来越接近真值,并且比原始量测数据曲线更为平滑.由于封闭空间中的噪声是平稳随机过程,具有各态历经特性,故统计特性基本稳定,因而不需要大量的样本,Kalman算法就能够达到比较满意的滤波效果.实验证明Kalman滤波算法对环境数据的处理能够有效地抑制系统过程噪声和量测噪声.从图8可以看出各参量的最终滤波误差均<2%,效果较为理想.最终结果如表4所示.

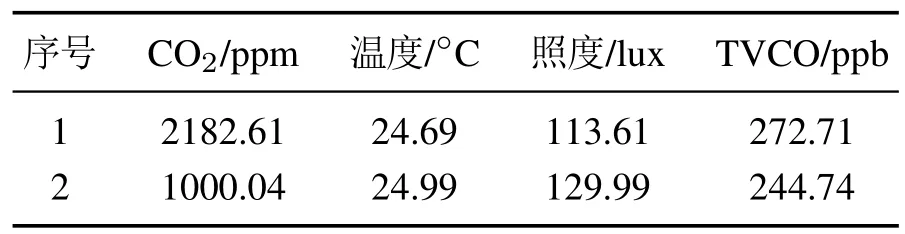
表4 Kalman滤波结果Table 4 Result of Kalman filtering

表4中Kalman滤波输出(第1组)作为输入到控制模型和神经网络模型的状态数据.神经网络输出值(第2组)作为控制模型的输出期望.图10分别给出了均值滤波和Kalman滤波的均方根误差(root mean square error,RMSE)随样本数的变化情况,其中

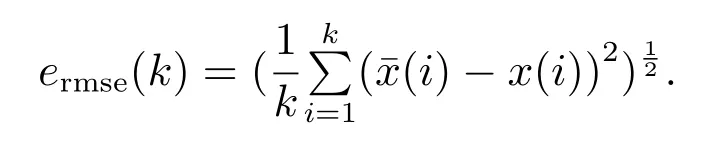
图7 CO2数据滤波过程Fig.7 The data filtering process of CO2

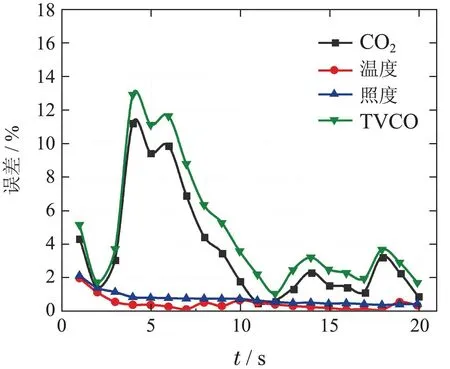
图8 Kalman滤波误差Fig.8 The errors of Kalman filtering

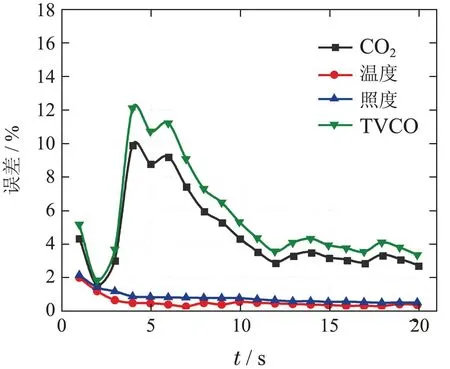
图9 均值滤波误差Fig.9 The errors of mean filtering

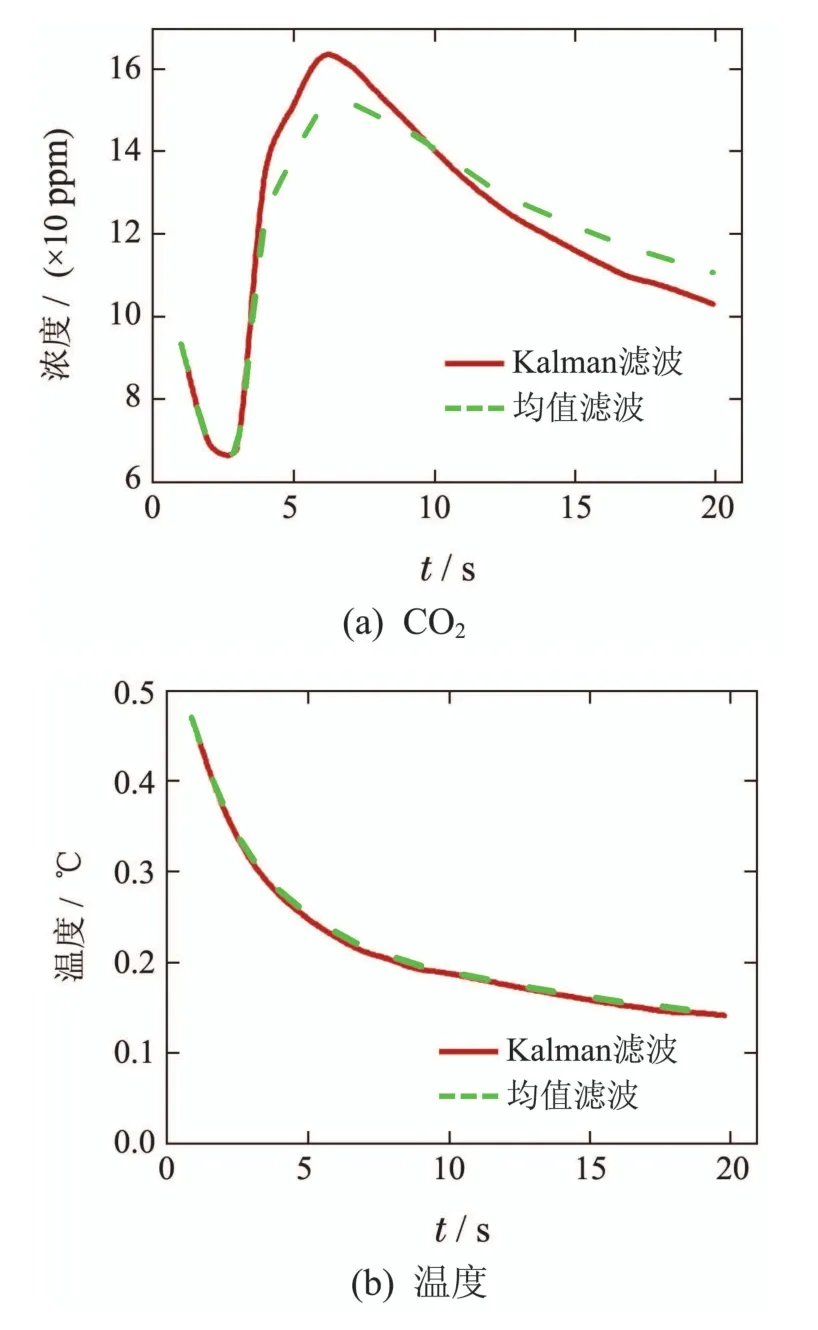
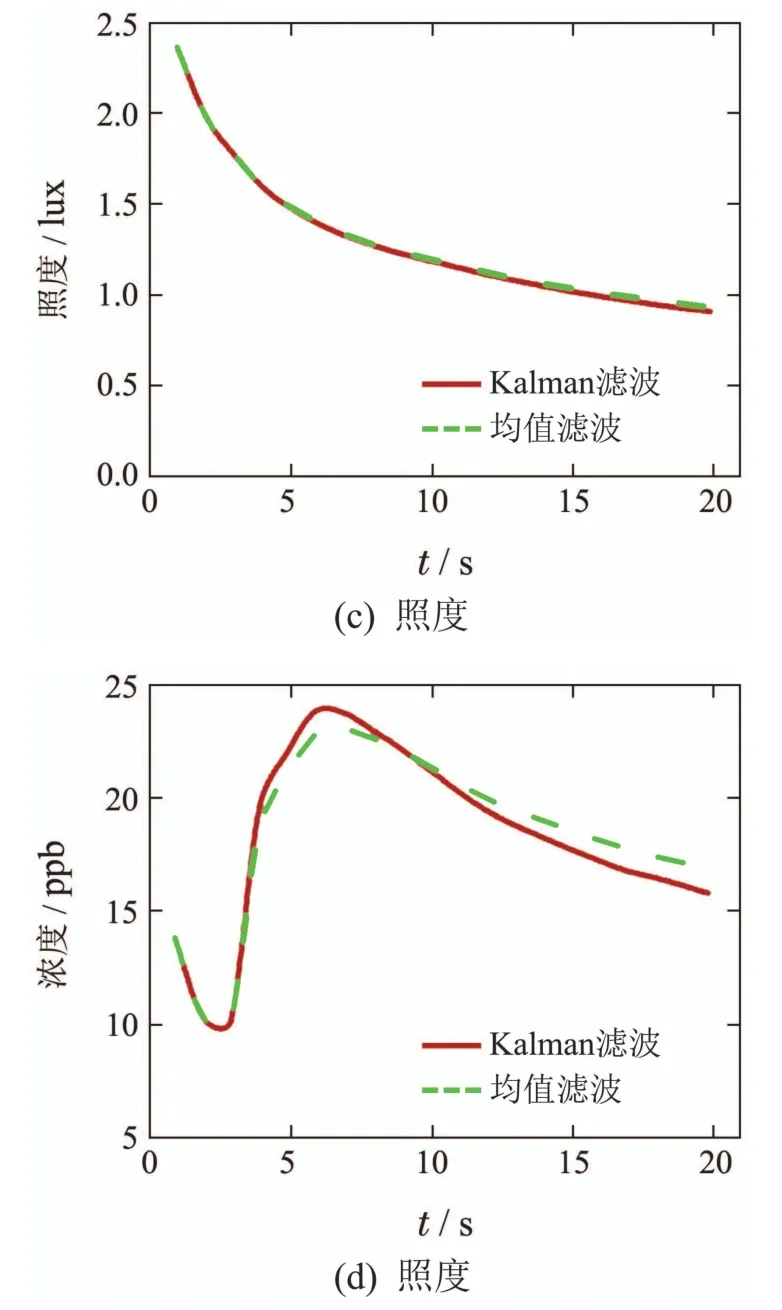
图10 均值滤波和卡尔曼滤波RMSE比较Fig.10 RMSE comparison between Kalman and mean filtering

可以看出,在后面的样本中,均值滤波的RMSE均大于Kalman滤波,可见,后者的精度要高于前者.

4.2 不同控制算法的调控效果分析

对比图11–12,可以发现,对于同一个环境系统的闭环调控,DMC控制器能够在迭代40次左右快速收敛,而PID控制器则需要在60次左右才开始收敛,因而在收敛速度、控制过程的稳定性以及控制精度上DMC控制器的效果都要优于PID控制器.最终的CO2、温度、照度、TVOC的调控误差分别为2.4×10−5,2.5×10−5,2.6×10−6,2.3×10−6.从系统的温度输出曲线可以发现PID算法存在超调现象:在实验数据中,当前温度的状态值已经接近期望值,此时只需要维持系统当前的输出状态即可,而不必改变控制量,即∆u(k)应为0,如图12(b)所示.此外,输入数据作为控制系统工作的起始状态,要求能够尽可能准确地反映当前环境的真实状态,数据的质量直接影响系统整体的调控性能,因此输入数据的预处理就显得至关重要.

4.3 不同控制算法的调控能耗分析

从图12可以看出,由于传统PID控制算法的局限性,使得在调节过程中容易出现超调、震荡现象,这将造成能耗的增加,图13分别给出了关于4种环境参量的DMC控制器(实线)和PID控制器(虚线)的输出控制量以及其相应的差值∆u(k)(阴影区域).图中DMC控制器的输出较为平缓,相反PID控制器的输出过于剧烈.经计算,采用DMC控制算法对CO2、温度、照度、TVOC进行优化调控分别能够有效节约5.63%,0.89%,0.33%,1.49%的能耗.

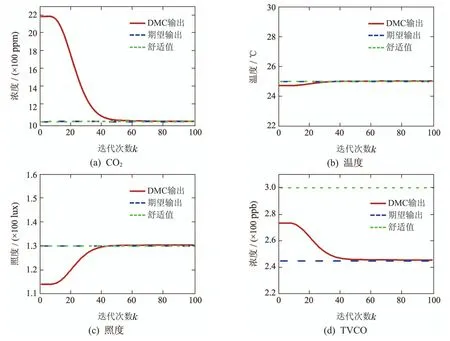
图11 经滤波后的DMC控制曲线Fig.11 Filtered DMC control curve

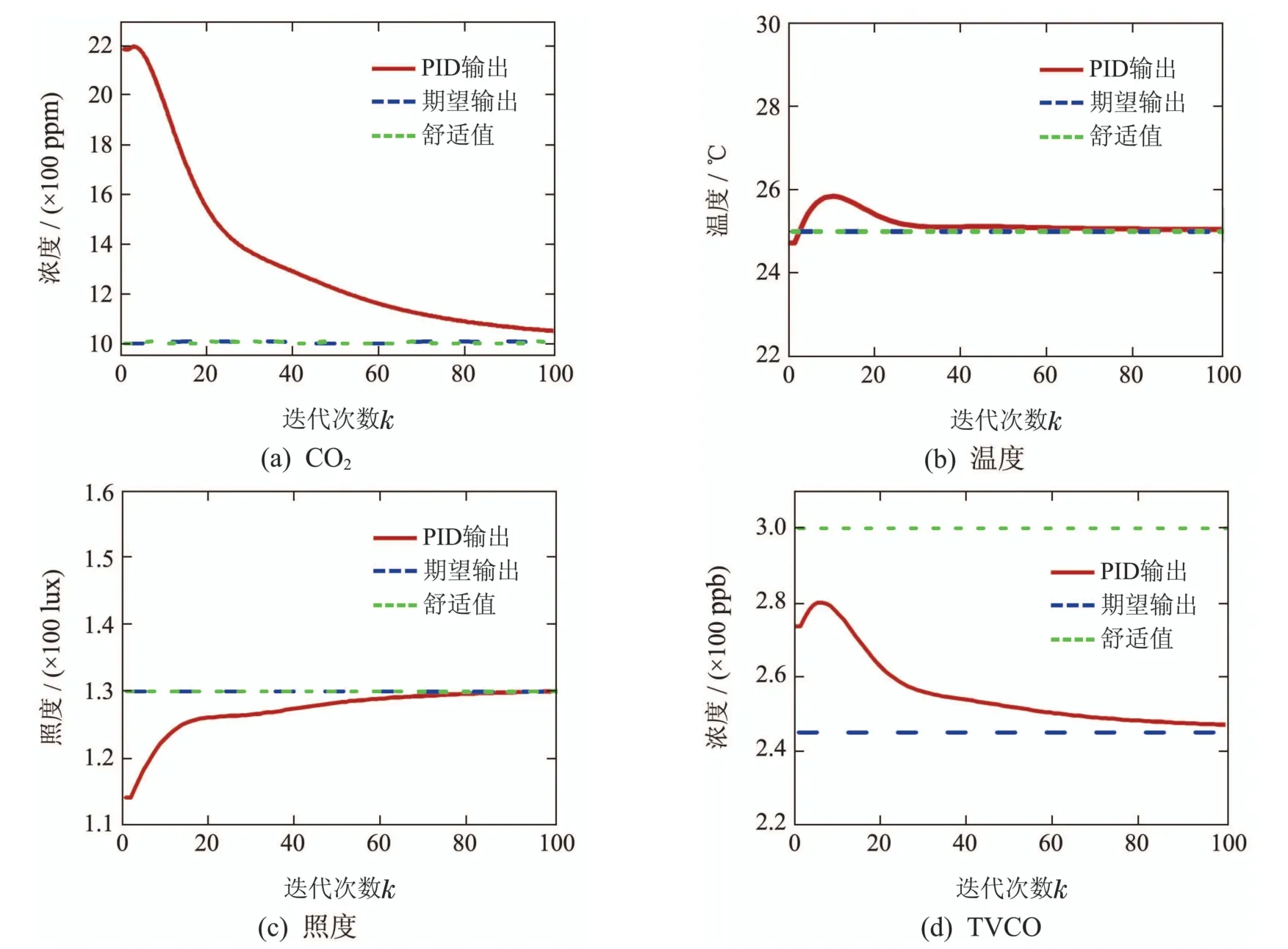
图12 经滤波后的PID控制曲线Fig.12 Filtered PID control curve

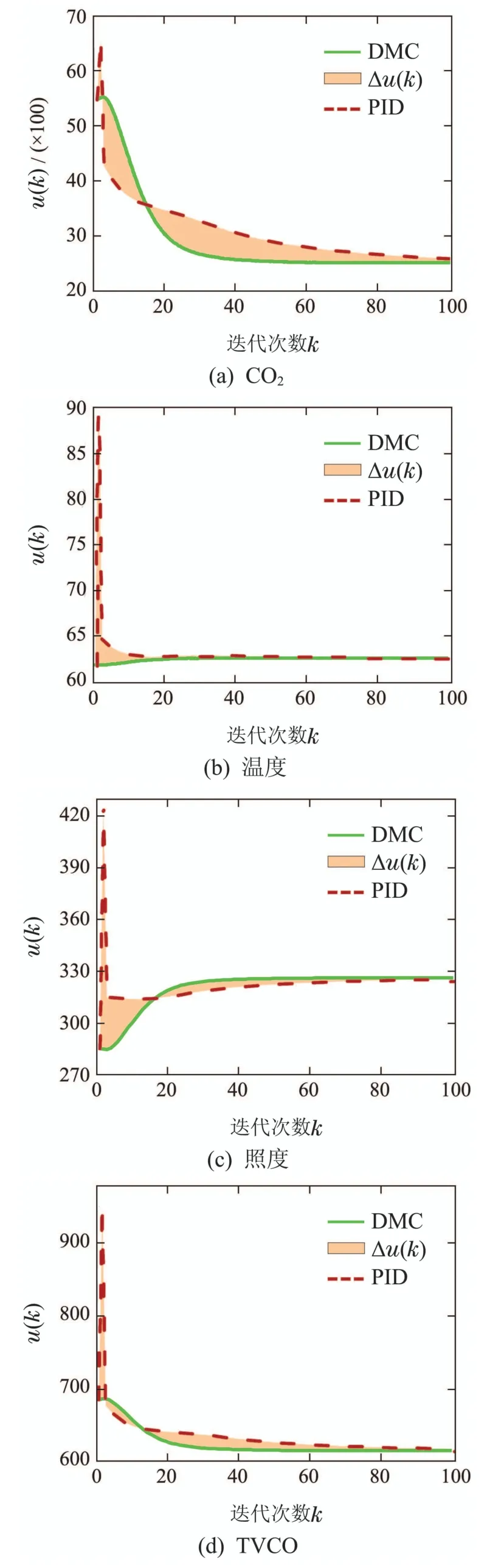
图13 DMC/PID控制器输出对比Fig.13 The output comparison with DMC and PID controller

5 结论

本文提出了一种可应用于室内环境闭环调控的综合建模方法,并以某实验室的冬季室内环境数据为例,对该方法进行仿真验证,实验中,数据滤波误差<2%,针对CO2、温度、照度、TVOC的调控误差分别为2.4×10−5,2.5×10−5,2.6×10−6,2.3×10−6,节能率分别为5.63%,0.89%,0.33%,1.49%.

仿真结果表明,此方法能够有效提高室内环境闭环控制系统的控制精度和抗干扰能力从而提高控制系统的鲁棒性,而且克服了传统增量式PID控制算法出现超调的现象,从节能角度来看效果也优于传统PID控制算法,非常适合用于封闭的室内环境调节.另外,该方法不仅仅适用于普通室内环境的自适应调控,还具有广泛的应用前景,可以推广应用于其他对环境因素要求比较苛刻的场合的精细调节,比如医院、温室、科研实验室等.