数据与未建模动态驱动的非线性PID切换控制

张亚军,牛 宏,柴天佑

(1.东北大学流程工业综合自动化国家重点实验室,辽宁沈阳 110819;2.辽宁石油化工大学理学院,辽宁抚顺 113001)

1 引言

对一类具有强非线性特性并难以建立精确数学模型的复杂过程控制系统,传统的方法大多首先采用实际过程的动态物料平衡原理建立其机理模型,将机理模型在工作点附近进行线性化得到控制器设计模型,并结合参数辨识算法以及未建模动态的智能估计算法进行直接或间接自适应控制器设计,如文[1–2]提出的随机非线性系统的自适应模糊控制方法以及纯反馈非线性系统的自适应控制方法、文[3–9]提出的采用模糊逻辑系统或者神经网络补偿系统未知非线性动态特性的自适应控制方法,文[10–13]提出的非线性模糊滑模切换控制方法等.上述控制方法对一些控制精度要求不很高的过程控制系统能取得较为理想的控制效果,但对于具有综合复杂性的系统将难以取得满意的控制效果.文[14–18]提出了基于神经网络与多模型的非线性切换控制算法和数据驱动控制[19–22]方法,是解决复杂工业过程控制的主要方法,但如果被控对象的机理不清,仍然存在难以选择合适的控制器结构的不足,这种情况下,即使通过大量的输入输出数据来校正控制器参数,也不能确保产生合适的控制输入,造成控制输入的波动,当控制器作用于被控对象时,难以取得良好的控制效果甚至造成系统不稳定[23].文[23]把基于模型的控制思想和数据驱动控制思想相结合,提出了一种新的虚拟未建模动态驱动的非线性控制方法,为解决一类机理不清,难以建立精确数学模型的复杂过程的控制问题提供了新途径.然而,文[23]的方法也是直接对未建模动态直接进行智能建模或者估计,并没有利用未建模动态前一时刻的历史数据信息,致使控制算法复杂,而且有可能增加未建模动态的估计误差,给系统带来潜在的影响.在此基础上,文[24]以氢氧化镍钴矿浆中和过程末槽出口矿浆pH值的控制为应用背景,利用了矿浆中和过程的可测数据以及未建模动态的历史数据提出了一种非线性控制方法并取得了一定的控制效果,但所提的方法并没有对未建模动态的未知增量进行估计和补偿,可能造成系统的瞬态性能欠佳.为此,本文采用文[25–26]的思想,首先利用被控对象可测的输入输出数据信息把被控对象表示成由低阶控制器设计模型与高阶非线性项(未建模动态)和的形式,在此基础上,把工业过程中普遍采用的PID控制与数据驱动、未建模动态估计与补偿技术充分融合,提出了一种新的基于数据与未建模动态补偿的非线性PID控制方法.所提方法克服了常规PID控制器只有出现偏差才开始调节控制器,从而产生滞后的缺陷,而且充分利用了被控对象的输入输出数据信息、未建模动态可测的历史数据信息以及非线性补偿技术,通过对未建模动态的未知增量采用自适应神经模糊推理系统(adaptivenetwork-based fuzzy inference system,ANFIS)进行智能估计并设计补偿器,尽可能地消除或减弱了其对闭环系统的影响,实现了较好的闭环控制效果.另一方面,为了合理的选择PID控制器参数以及未建模动态补偿器的参数,把一步超前最优控制策略与PID控制器设计相融合,从理论上给出了控制器参数选择的一般原则,保证了闭环系统的稳定性和收敛性.最后,将所提控制算法通过数值仿真和水箱液位控制系统的物理实验,实验结果表明了所提算法的有效性.

文章的组织结构如下:首先给出了控制问题描述;第3 节给出了基于数据与未建模动态驱动的非线性PID控制器设计方法、基于ANFIS的未建模动态增量估计算法以及控制器参数选择方案;第4节给出了闭环系统的动态特性分析;最后,给出了所提算法的数值仿真实验和在水箱液位系统的实验结果.

2 问题描述

一类难以用精确数学模型描述的非线性被控对象可以描述为

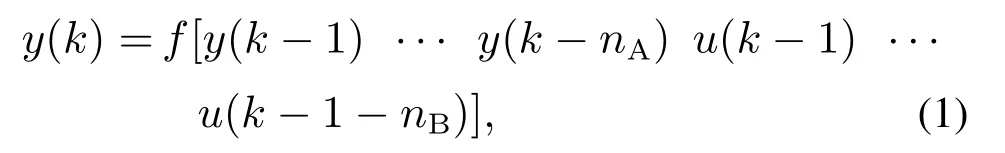
式中:u(k),y(k)分别为被控对象的输入和输出;nA和nB为模型阶次;f(·)∈R是未知的非线性函数.

利用被控对象的输入输出数据建立低阶控制器设计模型,并利用文[27]的思想,可将式(1)化为由低阶线性模型和非线性项组成的形式,即

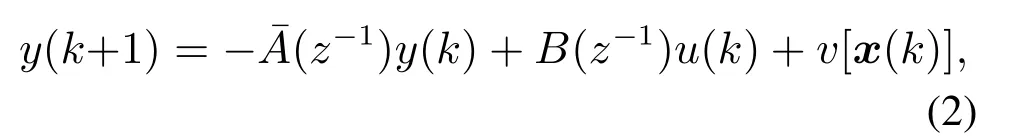
v[x(k)]为未建模动态,x(k)是维数为p=nA+nB+1的数据向量,且

模型式(2)可归结为下列的一般形式:

其中A(z−1)和B(z−1)分别为

其中nA和nB为模型阶次.

注1当时滞大于1时,可将本文的控制思想做相应的推广.

针对被控对象模型式(6),由于v[x(k)]未知,设计带有未建模动态补偿的非线性控制器时,需要对k时刻的未建模动态v[x(k)]进行估计.因此,v[x(k)]的准确估计是影响控制性能的关键.由于未知的未建模动态v[x(k)]可表示成前一拍可测部分v[x(k −1)]与未知的增量∆v(k)之和,即

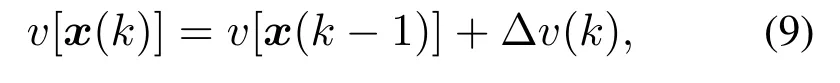
因此,模型式(6)可进一步的表示为

控制目标:针对非线性被控对象模型式(10),设计带有未建模动态前一拍数据补偿与未建模动态增量估计与补偿的非线性PID控制器,保证闭环系统的输入输出信号有界,使被控对象的输出y(k)跟踪参考输入w(k),并使其稳态误差小于或等于预先确定的值ε(ε>0),即

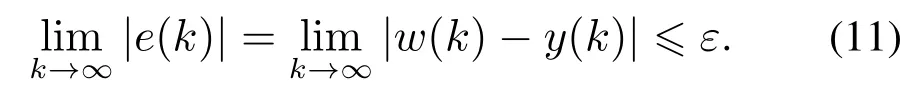
本文假设未建模动态v[x(k)]满足如下线性有界条件[23]:

条件1

其中0 ≤ε1<1,ε2>0均为已知常数.

3 非线性PID控制器设计

3.1 非线性PID控制器

本文提出一种新的带有未建模动态前一拍数据补偿及其增量补偿的非线性PID控制器,其结构如图1所示.

图1 带有未建模动态前一拍数据及其增量补偿的非线性PID控制器结构Fig.1 Nonlinear PID controller structure with unmodeled dynamics dynamics previous sampling data and incremental compensation

由图1所示的非线性PID控制器为

其中:KP,KI和KD分别为PID控制器的比例、积分和微分系数;是z−1的多项式;e(k)为跟踪误差,定义为

其中w(k)是理想输出.由式(13),利用单位迟滞算子z−1可以推出

其中:

把式(14)代入式(15)可进一步将式(15)写成如下形式:

将式(19)代入被控对象模型式(10)可得闭环系统方程为

为确定KP,KI,KD以及,可采用一步超前最优控制策略,为此,引入如下性能指标:

其中P(z−1),G(z−1),Q(z−1)和K(z−1)均为关于z−1的加权多项式.为了求得使性能指标式(23)极小的最优控制律,首先定义广义输出ϕ(k+1)为

广义理想输出y∗(k+1)定义为

广义输出误差eg(k+1)定义为

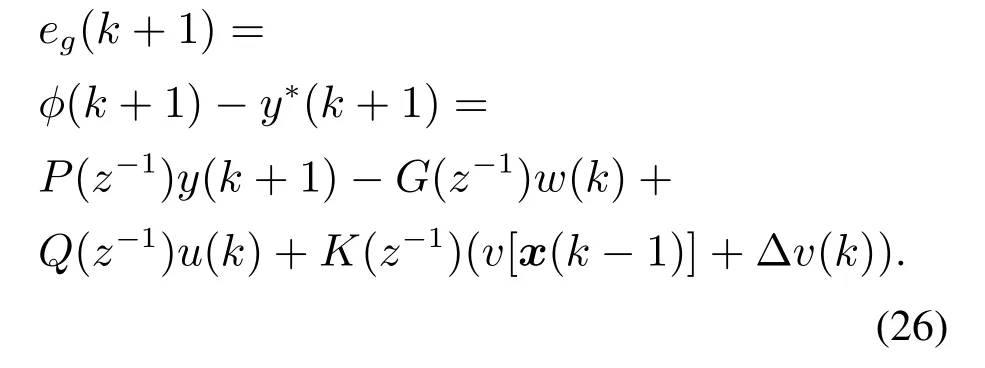
为了求取该最优控律,为此引入如下Diophantine方程:

其中F(z−1)和G(z−1)的阶次nF和nG分别为

由式(28)可得

选择G(z−1)的阶次nG=2,故,G(z−1)为

根据式(29),如果

则A(z−1)的阶次为三阶,即nA=3,P(z−1)的阶次满足nP≤2.

如果

则P(z−1)的阶次为nP=3,A(z−1)的阶次为nA≤2.

由式(10)(24)和式(27)可得

其中

由式(24)和式(34)可得

把式(36)代入式(23),使J最小可得带有未建模动态补偿的非线性PID控制律为

其中G(z−1)由Diophantine方程式(27)唯一确定.

由式(19)和式(37)可知,图6中所示的PID控制器参数与式(37)中的加权多项式的对应关系为

首先离线选择P(z−1)和Q(z−1)使得下式成立:

由选定的P(z−1),通过式(27)和式(39)可以获得,再通过式(16)–(18)可得PID控制器参数如下:

为了消除未建模动态v[x(k −1)]以及∆v(k)对闭环系统的影响,通过选定的Q(z−1),由式(22)(35)(38)以及式(40)可知选择K(z−1)应满足:

3.2 未建模动态增量估计算法

由于未建模动态的增量∆v(k)未知,故控制器(37)将无法实现.本文采用估计算法对∆v(k)进行估计,并通过补偿器的设计来消除未建模动态对闭环系统的影响.

类似于文[23],采用下面如图2所示的由数据处理、基于ANFIS估计器、误差校正器和∆v(k)的估计计算所组成的估计结构来估计未建模动态增量.

图2 未建模动态增量∆v(k)的估计算法结构Fig.2 Structure of the estimation algorithm for the unmodeled dynamics increment ∆v(k)

采用本文所提的未建模动态估计算法时,根据模糊系统的万能逼近定理[28],对任意的ξ≥0,一定存在一个理想的模糊系统使得

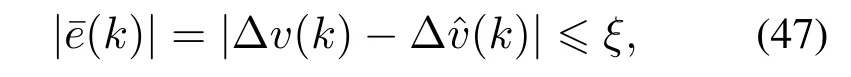
其中ξ是预先指定的任意小的误差限.

3.3 非线性PID切换控制

由于对未建模动态未知增量进行了估计,则带有未建模动态增量估计的非线性PID控制器方程为

当系统在工作点处时,不带未建模动态补偿的PID控制器方程为

上述控制器(48)–(49)通过切换机制协调控制系统,既保证系统的稳定,同时提高系统的性能.由于切换机制与文献[16]类似,为节省空间,这里不再赘述.

3.4 PID控制器参数选择

为了使PID控制器参数设计简单,本文选取低阶线性模型A(z−1)的阶次为nA=2,nB=1.由于G(z−1)的阶次为nG=2,则由式(27)可知,P(z−1)的阶次nP=3.不等式(41)给出了离线选择P(z−1)和Q(z−1)的原则.当nB>0时,式(45)只能求得K(z−1)的最小二乘解,可补偿未建模动态,但不能消除未建模动态.当k →∞,v[x(∞)]为常数时,选择K(z−1)的稳态值为K(1),并且满足

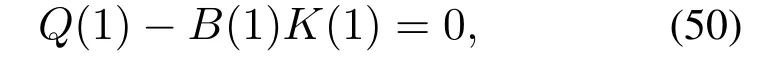
可消除v[x(∞)]对被控对象输出的影响.

设

由式(35)和式(38)可知

因为F=P(0)=p0,nB=1,所以,Q(z−1)为1阶多项式或者常数,即nQ=1或0.下面分两种情况来讨论.

假设1设Q(z−1)为z−1的1阶多项式,即

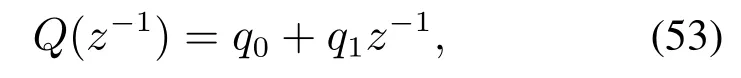
其中

假设2 如果设Q(z−1)为0阶多项式即常数,则

由式(35)(38)可得

其中p0满足

综上讨论可知,选择P(z−1)和Q(z−1)的原则是使闭环特征多项式T(z−1)为稳定的多项式,即

根据选定的P(z−1),由Diophantine方程式(27)可得G(z−1)的系数为

因此,PID参数计算公式如下:

根据式(45)可得补偿器K(z−1)为

由于nB=1,由式(49)可知,满足式(61)的K(z−1)只能有最小二乘解.

4 性能分析

控制器设计必须首先保证闭环系统的稳定性,即系统的输入和输出是有界的,即

并且使得被控对象的输出y(k)与参考输入w(k)之间的跟踪误差满足式(11).

为了说明当未建模动态满足条件1的假设时,本文所提的控制算法能保证闭环系统的稳定性,下面首先建立闭环系统方程,即引理1.

引理1当带有未建模动态前一拍数据补偿及其增量估计与补偿的非线性PID控制器式(48)作用于被控对象式(10)时,闭环系统的输入输出方程为

其中Γ(z−1)=P(z−1)B(z−1)+Q(z−1)A(z−1).

证由式(34)和式(37)可得

B(z−1)乘以式(63)两边,Q(z−1)乘式(10)两边,并利用式(47)可得

A(z−1)乘以式(63)两边,并利用式(10)和式(47)可得

联立式(64)和式(65)可得方程(62). 证毕.

定理1假定被控对象式(10)满足下列条件:

①v[x(k)]满足条件1.

②凑试P(z−1)和Q(z−1)使其满足

选择K(z−1)使其在最小二乘意义下满足

并且在稳态时满足

③存在一个理想的ANFIS,使得未建模动态增量的估计误差满足式(47).则存在一个正常数β1使得当ε1<β1时,所提的非线性PID控制器式(48)作用于被控对象(10)时,闭环系统的输入输出信号一致有界(BIBO稳定),即

并且,闭环系统的稳态跟踪误差e(k)的绝对值小于或等于预先确定的值ε(ε>0),即

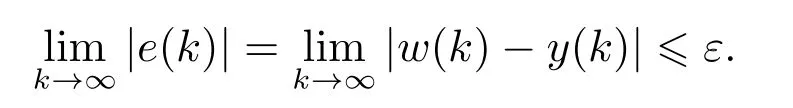
证由引理1,根据闭环系统方程式(62)的特征多项式矩阵的稳定性,采用类似于文[24]的证明方法容易证得定理1的结论成立,这里不再赘述. 证毕.

5 数值仿真及水箱液位系统的控制实验

5.1 仿真1

为了说明本文提出的控制算法的有效性,考虑如下的离散时间非线性系统.

其中:原点是系统的平衡点,d(k)=0.01.

显然,系统的阶次nA=2,mB=1.系统的参数多项式为

显然,该非线性系统Taylor展开后的线性控制器设计模型为

则线性控制器设计模型与被控对象之间的未建模动态为

其中x(k)=[y(k)y(k −1)u(k)u(k −1)]T.由式(12)可知

离线选择加权项

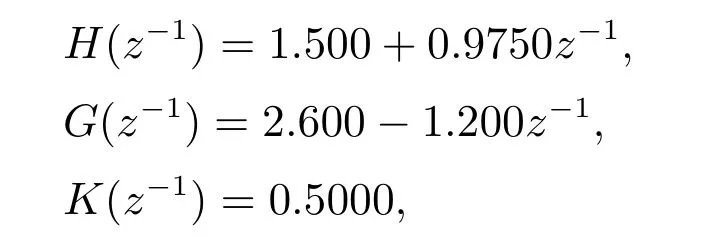
则闭环系统的特征多项式为

其特征根分别为−0.6500,0.4333±0.4607i,均在单位圆内.

控制目标为使闭环系统的输出y(k)跟踪有界参考输入信号:

凑试ε1=0.001,ε2=0.0001.未建模动态增量估计算法中ANFIS的隶属度函数选为高斯型,对每个输入量划分为3个模糊子集;实验结果如图3–6所示.

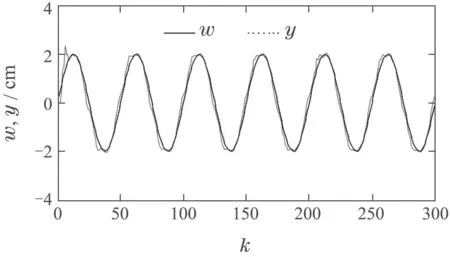
图3 数据与未建模动态驱动的PID控制系统的性能(输出y,参考输入w)Fig.3 Performance of the PID control system based on data and unmodeled dynamics driven(output y,reference input w)

图4 控制输入uFig.4 Control input u

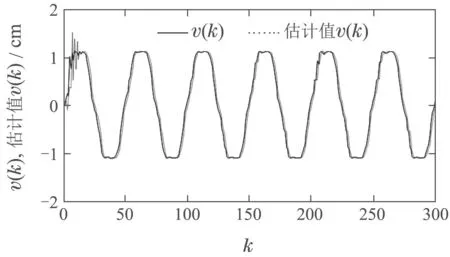
图5 未建模动态及其估计值Fig.5 Unmodeled dynamics and its estimated value

图6 估计误差Fig.6 Estimation error

图3是采用本文提出的非线性控制算法以及未建模动态估计算法时闭环系统的输出响应.从图中可以看出,采用本文的控制算法提高了闭环系统的跟踪特性,闭环系统的输出达到了跟踪给定参考输入的要求,超调量和跟踪误差都很小,有效改善了闭环系统的性能.

图4是控制器的输出曲线.

图5给出了未建模动态的实际值以及采用本文的估计算法所得到的估计值的曲线.从图中可以看出,本文的估计算法有效地估计出未建模动态的大小.

图6是估计误差,从图中可以看出,估计误差随着控制器输出量的增加而增大,这也从另一方面说明了本文的控制算法适合于控制一类控制器增量非突变的非线性系统,如果控制器变化非常剧烈,则估计误差也会随着增大,从而会导致闭环系统的跟踪特性的下降.

5.2 仿真2–水箱液位控制实验

水箱控制系统的实物结构如图7所示,主要由水箱、比例阀门、水泵、储水箱、散热风扇和加热器等组成.由于本文主要针对水箱液位控制系统进行研究.因此,在图7中,标出了与水箱液位实验有关的实物名称,并给出了水箱液位系统的结构框图,如图8所示.

水箱液位系统的控制目标是通过调节水泵的脉宽调制(pulse width modulation,PWM)占空比,从而u(k)改变水泵的电压,使得水箱的液位快速的保y(k)持在预设定的高度.

图7 水箱控制系统Fig.7 Tank-level control system

图7所示的液位系统由水泵、流量传感器、液位传感器、泄水阀、水箱和控制器组成.其中,总的供水量由水泵提供,比例阀门控制水箱的进水流量,液位计可以实时测量水箱的液位值,泄水阀保持全开状态,水泵从蓄水池抽水,水流经过流量传感器进入水箱,最后由泄水阀门排入蓄水池,形成水流回路.图7和图8中所涉及到的符号含义如表1所示.

将本文所提的方法应用在多功能过程控制实验台上进行水箱液位控制实验.实验中,液位的设定值开始为6 cm,w=660 s后设定值变为8cm.根据水箱系统的输入输出模型运用本文所提的方法进行控制器设计,利用控制算法软件包Easycontrol进行算法的编程,然后下载到控制器中实现对单容水箱液位的控制,实验中,采样周期为0.1 s.选择为三阶多P(z−1)项式,即

表1 水箱液位控制工艺过程原理图中所涉及到的符号含义Table 1 Symbolic meaning involved in schematic of schematic diagram of tank level control process

选择Q(z−1)为一阶多项式,即

经验证闭环方程的特征根均在单位圆内,因此闭环系统稳定.根据公式(60)可得PID控制器的参数以及补偿器的最小二K(z−1)=k0+k1z−1乘解分别为

其中:ε1=0.003,ε2=0.001.NFIS采用网格划分法对输入空间进行划分,每个输入量被划分为3个模糊区间,隶属函数选为“高斯型”.实验结果如图9–11所示.

作为对比,在保持PID参数不变的情况下,采用常规的PID控制器进行水箱的液位控制,实验结果如图12–14所示.

从图12–14的实验结果来看,本文提出的控制算法具有良好的跟踪特性,所设计的PID控制器参数以及补偿器能实现了较好的控制效果.

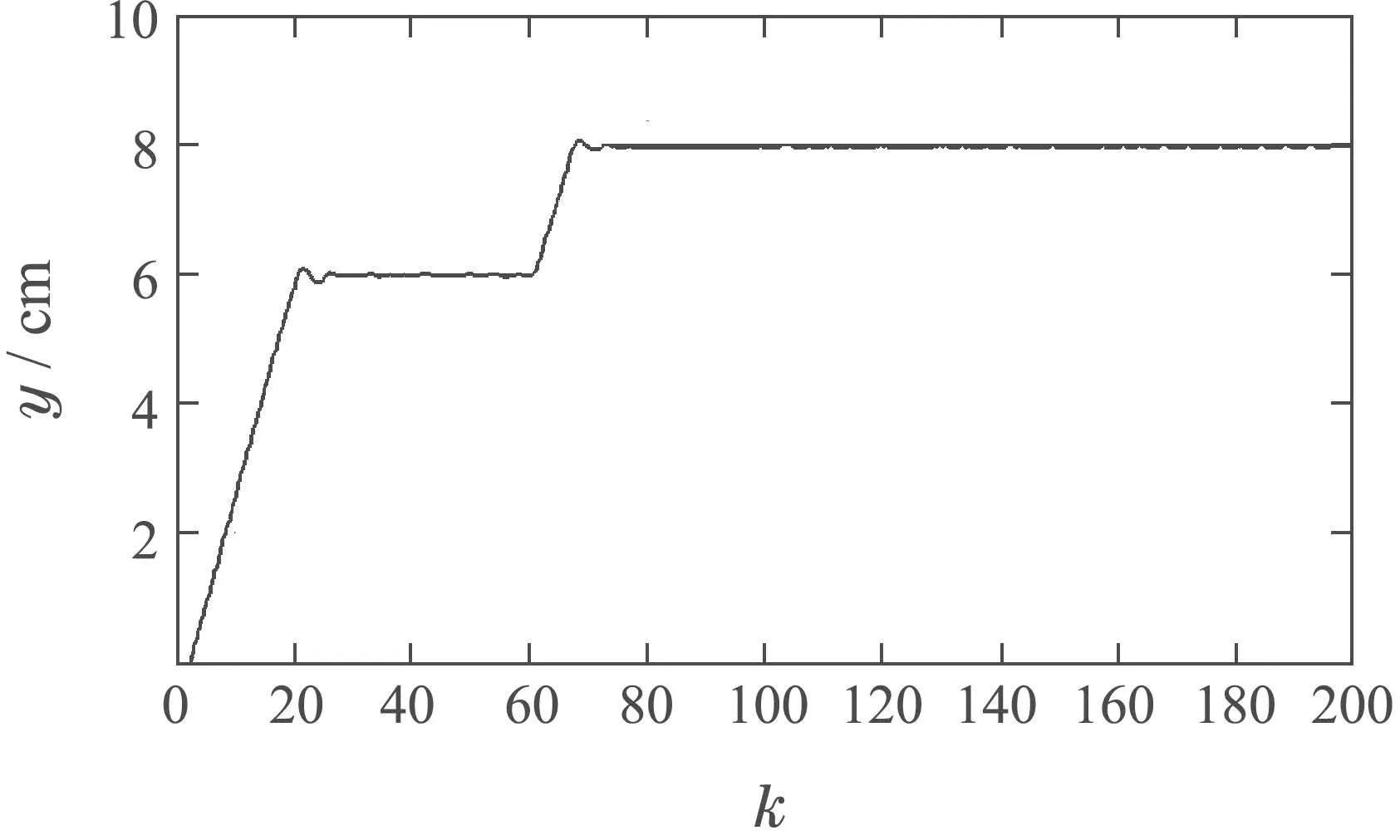
图9 采用本文方法时水箱液位的实际响应曲线(输出y)Fig.9 Actual response curve of tank level using the proposed method(output y)

图11 采用本文方法时水箱的未建模动态v[x(k)]Fig.11 Unmodeled dynamics v[x(k)]of tank using the proposed method

图12 采用常规PID控制器时水箱液位的实际响应曲线(输出y)Fig.12 Actual response curve of tank level using the traditional PID Controller(output y)

图13 采用常规PID控制器时水箱液位的控制输入uFig.13 Control input u of tank level using the traditional PID controller u

图14 采用常规PID控制器时水箱液位的未建模动态v[x(k)]Fig.14 Unmodeled dynamics v[x(k)]of tank level using the traditional PID controller

比较图12和图14可以看出,由于对采用了未建模动态的历史数据以及未知增量进行了动态补偿,系统输出跟踪设定值的效果优于不带补偿的常规PID控制器.

6 结论

本文针对一类难以建立精确数学模型的复杂工业过程在工作点附近采用常规控制算法难以进行有效控制的问题,提出了一种基于数据和未建模动态前一拍数据及其未知增量估计与补偿的非线性PID控制算法.该算法的优势在于充分利用了被控对象的输入输出数据以及未建模动态的历史数据信息,改进了控制算法,并将一步超前最优控制理论与常规PID控制算法相结合,给出了一种设计PID控制器参数的方法,分析了所提控制方法的稳定性和收敛性,最后通过水箱液位控制系统的物理实验,实验结果验证了所提算法的有效性和实用性.