基于多搜索器优化算法的含可再生能源协同优化调度

2020-05-12唐建林张孝顺李卓环陈俊斌

控制理论与应用 2020年3期

唐建林,余涛,张孝顺,李卓环,陈俊斌

(1.华南理工大学电力学院,广东广州 510640;2.汕头大学工学院,广东汕头 515063)

1 引言

随着化石燃料的消耗以及日趋严重的全球变暖形势,可再生能源和高效能源实用技术正引起广泛关注[1].为了解决当前能源短缺、环境恶化问题,世界众多国家都开始调整能源布局,需找新的能源发展方式、提高能源利用率.

在转变能源发展方式、调整能源结构上,人们开始更多的关注以风力发电和光伏发电为代表的可再生能源发电方式[2].这种分布式发电方式具有投资小、占地少、节能环保等优点[3].由于风力发电和光伏发电时输出功率的随机性和波动性,传统的经济调度方法已经不再适用[4].以往的多数研究中没有考虑风力发电、光伏发电产生的成本,在分析计算中均将风电、光电等效成只发电却不产生成本的发电机[5].这种处理方式并没有考虑风电、光电的随机性、波动性对电力系统装机容量提出的额外要求,这势必会对经济调度分析结果的客观性产生影响.

电力系统和热力系统具有天然的互补性,对二者进行统一调度能够在更广的时空范围内提高资源优化配置的能力和能量的利用效率.我国大型风电场、光伏电场集中的北方地区,现有常规机组中50%～70%的发电机组为热电联产[6].高渗透率风电、光电与高比例热电联产机组占主导的电源结构,给电力系统调度和控制带来了巨大挑战.

为了实现风力机组、光伏机组和热电联产机组的综合利用,对热电经济调度(combined heat and power economic dispatch,CHPED)进行优化,在满足系统所有不等式和等式约束的同时,实现了最优的发电调度和供热调度,使供电和供热的总成本降至最低.处理该问题的方法主要有两大类,第一类是以二次规划法[7]、内点法[8]、牛顿法[9]为代表的经典优化算法.它们在求解经济调度问题依赖具体的数学模型且如果系统是非线性的,均在不连续函数和约束时,容易得到局部最优解.虽然应用Cplex等成熟数学求解器可以实现对经济调度的快速求解,但是其模型应用设计比较繁琐.第二类是启发式人工智能算法.遗传算法(genetic algorithm,GA)[10]、粒子群算法(particle swarm optimization,PSO)[11]、差分进化算法(differential evolution algorithm,DE)[12]、灰狼优化算法(grey wolf optimizer,GWO)[13]等智能算法对具体的数学模型要求程度低,应用更简便,在电力系统各类优化问题上已有较为成熟的应用.然而大多数算法都有其各自的弱点,主要特征如下:

1)种群的初始化完全随机,无法提高解的多样性,从而无法避免减少过早收敛问题.

2)求解优化问题效率低下,大部分智能算法采用单一的群体搜索一个潜在的全局最优解,很容易陷入低质量的局部最优解.考虑到发电机的阀点效应和热电联产系统的非凸不等式约束,CHPED问题是一个高度非线性、非光滑、非凸的问题,需要强大的优化方法来求解,以避免陷入局部最优解.本文提出一种新的基于混沌映射理论的优化算法.该算法因其内部具有多层次的搜索器结构,被称为“多搜索器优化算法”.根据3种不同类型的测试函数和27机组热电系统仿真得到的结果,表明多搜索器优化算法在非线性、非光滑、非凸的优化问题上是有用的,并且效果显著.

2 经济调度数学模型

2.1 可再生能源模型

这一部分主要介绍风速和太阳光照的模拟情况与功率输出的关系.

2.1.1 风速和功率输出的关系

风速的概率分布参数是最能体现当地风资源统计特性的指标,同时也是风力发电研究中的重要参数.有很多种模型可用来近似拟合风速概率分布,主要包括威布尔分布、瑞利分布、对数正态分布和正态分布等多种函数.由于两参数威布尔模型可调整参数来适应风速的周期变化,所以在风速的概率建模分中应用非常广泛.服从威布尔分布的概率密度函数定义如下[14]:

相应的累积分布函数为

式中:V为风速随机变量;v为风速;k为风速概率分布函数的形状参数,它决定了风速概率分布密度曲线的总体形状;c为尺度参数,反应风场的平均风速,起放大或缩小曲线的作用,但不影响分布密度曲线的形状.

假设风力发电机的输出特性是一个简化的分段线性函数,对于给定的风速v,其输出功率定义如下[15]:

式中:pwt为单台风力机组的输出功率;为额定功率;vin为风力机组的切入风速;vr为风力机组的额定风速;vout为风力机组的切出风速.

通过如下的线性变换,将风速的概率分布转变为风电的概率分布[16]:

式中:T为一般情况的变化函数形式;PWT为风电随机变量;V为风速随机变量.

对于威布尔函数来说,风电输出功率随机变量的离散部分如下:

当风机的输出功率处于连续变化的范围内时,其威布尔的概率密度函数如下式:

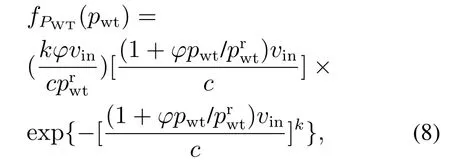
式中φ=(vr−vin)/vin.

2.1.2 太阳光照和功率输出的关系

根据统计数据,太阳的光照强度在一定时间段内可以近视地认为服从Beta分布,它的概率密度函数如下所示[17]:

式中:rmax为最大光照强度;r为实际光照强度;µ为数学期望;σ为标准差.

光伏系统的输出功率与光照强度近视成线性关系,不考虑功率损耗,且忽略环境温度的影响,则可以得到下式[18]:

式中:A为光伏电池阵列总面积;η为光伏组件总的光电转化效率.从而,可以推导出光伏电池的概率密度函数如下:

式中:ppv为光伏系统的输出功率;为光伏系统的最大输出系统.

2.2 成本函数

2.2.1 目标函数

整个系统的架构如图1所示,供给侧主要由燃气发电厂、热电联产装置、供热厂、风电场和光伏电厂所构成,它们产生的电和热分别通过线路和管道进行传输到达需求侧.

图1 含可再生能源的系统框架Fig.1 System framework with renewable energy

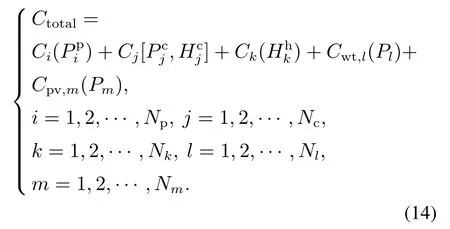
其目标是使整个系统的总生产成本最小.

2.2.2 仅供电成本

通常情况下,燃料成本可以用二次函数来表示,但是在实际操作中,大型发电机组通常含有多气门汽轮机,当蒸汽进气阀开始启动时,由于拉丝效应,燃油损耗将会急剧增加从而导致燃油成本的增加,会在机组耗量曲线上叠加一个脉动效果,产生了阀点效应.为了更加精确地表示发电机组的发电费用,实际上需要在原来二次函数的基础上,再叠加一个正弦函数,这将增加非光滑和非凸的特性,其耗量特性曲线方程如图2所示[19].

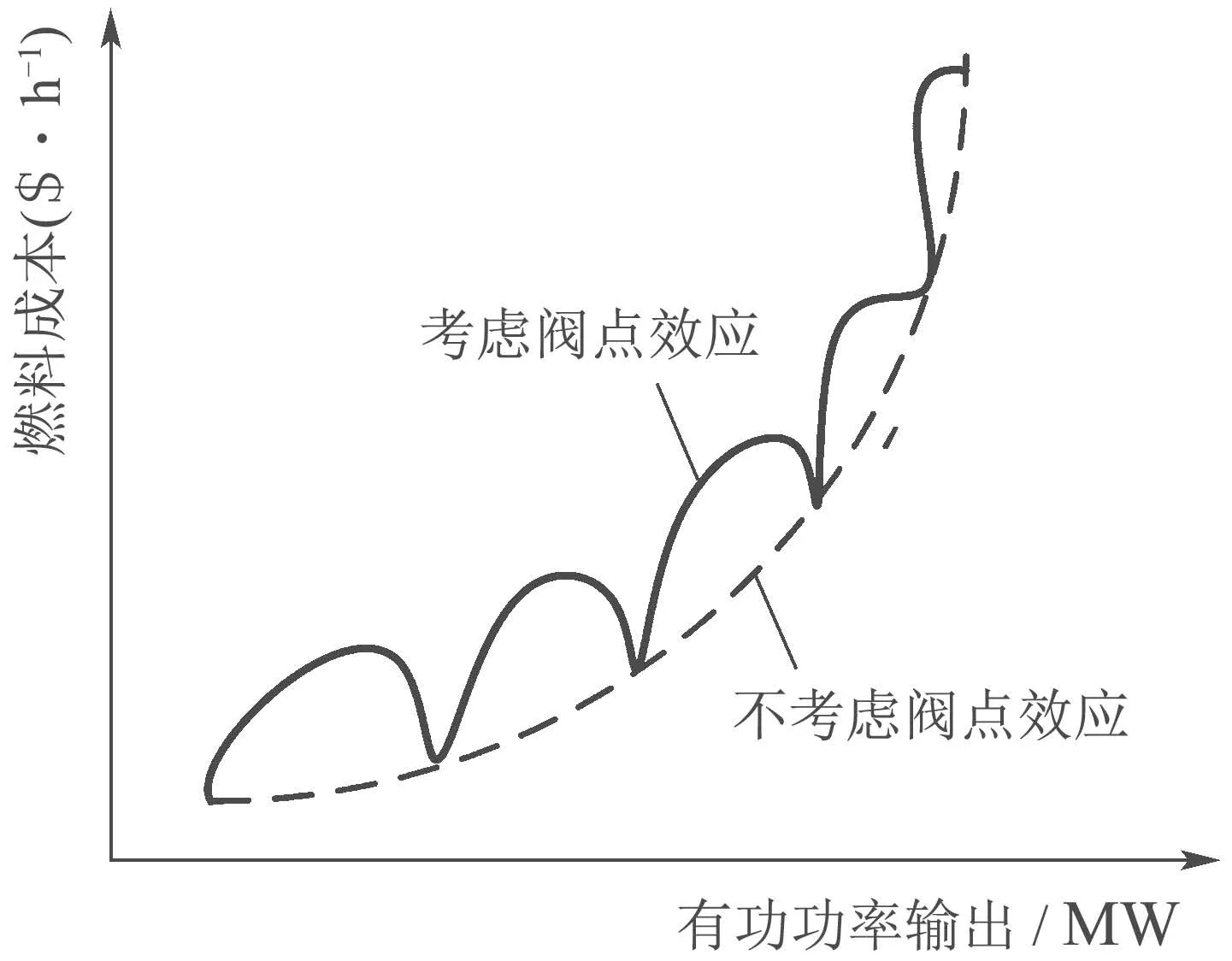
图2 阀点效应Fig.2 Valve-point loading effect

2.2.3 热电联产成本

热电联产机组不仅能实现热与电负荷的供应,还能减少污染气体排放,具有良好的社会效益和经济效益,其成本函数如下[20]:

2.2.4 仅供热成本

产热机组的成本函数如下式[21]:

式中:ak,bk,ck为成本系数;为产热量;Nk为仅供热机组的数量.

2.2.5 风力发电成本

通常情况下,风力发电厂由私人所有,电网运营商需要根据电力购买协议从风力发电商购买电力,需要支付一定的费用[22].其费用包含3个部分.第1部分是购买风力的直接成本.

式中dwt,l为风电的直接成本系数.

第2部分是低估了风电出力而导致的惩罚成本.由于风力发电的波动性很大,风电预测通常会有一些误差.当计划的风力发电量低于可利用的风力发电量时,多余的风能就会被浪费.

式中:Kue,wt,l分别为风电的低估系数;Pwt,rate,l为第l台风力机组的额定功率;Pwt,l为第l台风力机组的计划输出功率.

第3部分是高估风电出力而产生的辅助服务成本.如果按照计划的风力发电高于实际可用的风力发电,那么就应该通过其他地方获得备用电源来满足负荷需求.

式中Koe,wt,l为风电的高估成本.

总的风力发电成本如下:

2.2.6 光伏发电成本

光伏发电的成本函数类似于风力发电,也是由3部分构成[22].

式中:dpv,m为光电的直接成本系数;Kue,pv,m为光电的低估系数;Koe,pv,m为光电的高估系数.

总的光伏发电成本如下:

2.3 约束条件

2.3.1 等式约束

燃油机组、热电联产机组、风力机组和光伏发电机组的电力平衡约束由等式约束来表示,热电联产机组和产热机组的热平衡约束也由等式约束来表示.

式中:Pd为电负荷需求功率;Hd为热负荷需求功率.

2.3.2 不等式约束

1)纯发电机组的运行约束为式(28)、热电联产机组中关于电和热的运行约束为式(32)和式(33)、风力发电的运行约束为式(29)、光伏发电的运行约束为式(30)、纯发热机组的运行约束为式(31):

2)对于热电联产机组,图3表示了热电联产机组的热电耦合关系,是由定点ABCDEF连线所围成的封闭区域,沿着区域的边界线段BC,机组发热量递增,出力递减,而沿着线段CD机组发热量则递减[23].

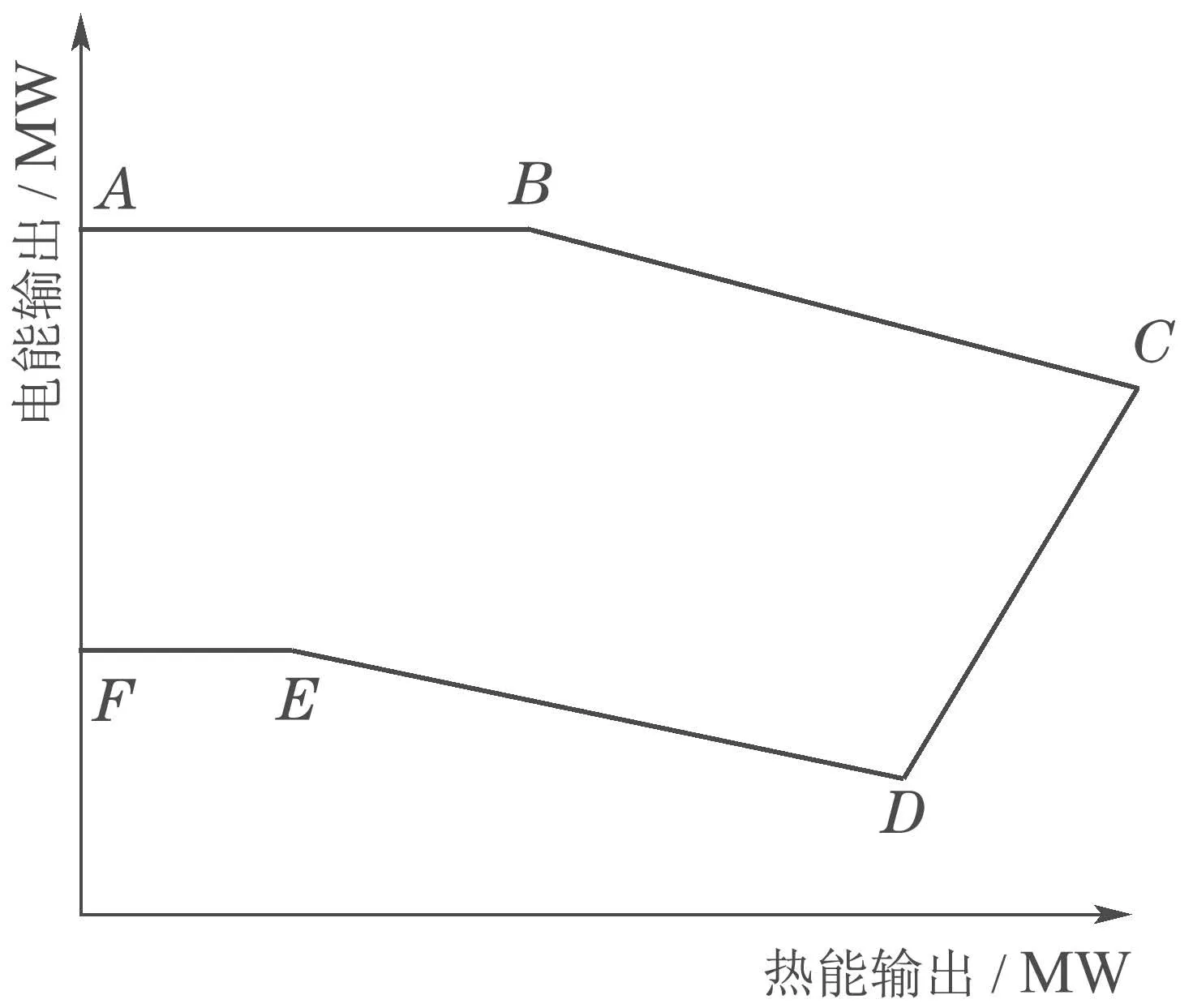
图3 热电联产装置运行区域Fig.3 Feasible operation region of the CHP units

3 多搜索器优化算法

本节主要介绍多搜索器优化算法.大多数启发式算法的灵感来自大自然,人们从大自然的运行规律中找到了许多解决实际问题的方法.但是多跟踪器优化算法并不是受自然的启发,而是根据其他算法的优点和缺点设计出来的,并且整合了混沌理论.

3.1 混沌理论

在许多实际的系统中,混沌是一种无处不在的非线性现象.混沌运动可以根据自身的规律性和遍历性,达到一定规模的每一个状态,这比简单的随机搜索算法要好.混沌搜索具有随机性、遍历性和规律性.因此,在许多优化算法中,通常利用混沌理论引入初始化解或替换算法中的随机参数以增强遍历性并加速全局最优收敛.由于混沌的非重复特性,基于混沌映射的算法比原来的算法更具有更全面的搜索能力.该特性是算法从局部最优中逃逸的关键,避免了过早收敛[24].

多搜索器优化算法在初始化的过程中使用了Logistic映射公式来产生具有混沌状态的混沌变量,混沌迭代公式如下式所示:

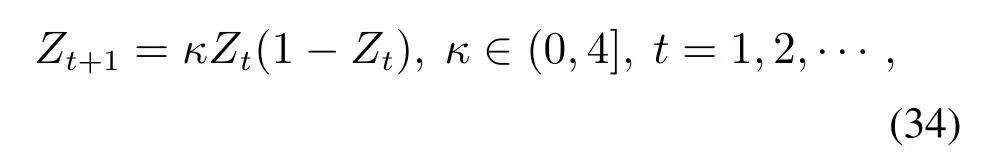
式中:0 ≤Z0≤1,Zt个变量;κ为控制变量,当选κ=4时,系统处于完全混沌状态,其混沌空间为[0,1].

随机产生一个n维且各分量值均在0～1之间的混沌矢量Zl=(zl1,zl2,···,zln)作为第1个种群.以Z1为初始值按照式(34)进行N −1迭代搜索计算,就得到N个矢量Z1,Z2,···,ZN.将产生的混沌矢量Zi(i=1,2,···,N)的各分量按式(35)映射到式(28)–(31)的约束范围,就可以得到各机组的发电功率和发热量的初始化状态,完成种群的初始化过程:

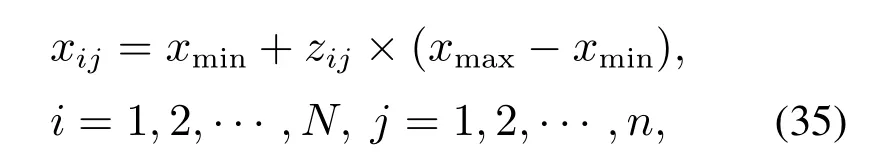
式中xmax和xmin为优化变量的上、下限.

3.2 双层搜索器

在搜索区域内随机分布一系列搜索器,被称为“全局搜索器”,并命名为GS.围绕在每个全局搜索器附近,并在指定半径内以此搜索器为中心,随机分布了另外一些搜索器,被称为“局部搜索器”,命名为LS,这些局部搜索器服从全局搜索器.设立局部搜索器的目的是为了在每个全局搜索器附近能够感知周围的动态变化过程然后进行局部搜索,当全局搜索器搜索完后,局部搜索器便展开后续搜索.这一特性能够提高收敛速度,避免局部最优.

全局搜索器的搜索半径的计算如式(36),它取决于跟全局最优点的距离和每个全局搜索器的等级:

式中:rmin和rmax分别为预先设定的最小半径和最大半径;kGS定义为全局搜索器的等级,当全局搜索器优化后的目标值最小时,kGS为0,以此类推,当全局搜索器得到的目标值最大时,kGS为最大;nGS为全局搜索器的个数;Gbest定义为全局最优解;dist(GS,Gbest)定义了全局搜索器跟全局最优点之间的距离.

3.3 随机游走规则

当局部搜索器的搜索结束后,为了全局搜索器能够找到最优点,全局搜索器开始进行随机游走.随机游走规则见图4,已经成功应用于很多算法里面[25].从一个点随机游走到另一个点,需要考虑两个变量:距离和方向角,其中距离用d来表示,方向角用Θ来表示.

其中w为π/4.

图4 全局搜索器游走规则Fig.4 Global searcher walking rules

当所有的全局搜索器按照随机游走规则移动就可以得到新的位置,所得到的解跟目前的全局最优解Gbest进行比较,如果效果更好,全局最优解将会被替换.

3.4 约束条件处理

本文采用罚函数法把系统的约束条件引入到目标函数中,通过罚函数法处理不等式约束,并保留等式约束的可行解,以避免算法出现“越限”现象.将等式约束优化转换为无等式约束问题,采用一个惩罚系数M构建的适应度函数为

显然,当满足等式约束条件时,此时罚函数为0,适应度函数的值即为成本函数.

3.5 算法流程

本文所提算法的求解流程图如图5所示.

图5 多搜索器优化算法流程图Fig.5 Flow chart of multi searcher algorithm

4 算例分析

为了测试所提算法在电力系统经济调度模型中的求解性能,本文引入10种不依赖于具体数学模型的智能算法与多搜索器优化算法进行求解效率的对比,分别是生物地理学优化算法(biogeography-based optimization,BBO)[26]、文化算法(cultural algorithms,CA)[27]、萤火虫算法(firefly algorithm,FA)[28]、遗传算法(genetic algorithm,GA)[10]、灰狼优化算法(grey wolf optimizer,GWO)[13]、飞蛾扑火算法(moth-flame optimization,MFO)[29]、粒子群优化算法(particle swarm optimization,PSO)[11]、模拟退火算法(simulated annealing,SA)[30]、教与学优化算法(teach-learn based optimization algorithm,TLBO)[31]和改进遗传算法(proposed genetic algorithms,PGA)[32].

根据上述的仿真模型以及大量的测试结果,本文的所有的算法参数设置如表1 所示.仿真计算均在CPU为英特尔Core i7–6700、主频3.4 GHz、内存16 GB的计算机运行.

表1 算法主要参数设置Table 1 Parameter setting of algorithms

4.1 标准测试函数

为了验证算法的有效性,下面将选择3种不同类型的函数进行数值实验.迭代步数均设为100.

Sphere 函数是较为简单的单峰函数,可以考察算法的收敛速度:

全局最优点为xi=0,f(x)=0.单峰函数中的适应度收敛曲线对比结果如图6所示,可以看出MFO无法收敛到全局最优,MSO的收敛速度最快,PGA的收敛速度次之.

图6 11个算法在单峰测试函数中的适应度函数收敛曲线对比Fig.6 Comparison of convergence curves of eleven algorithms in single peak test function

Step函数是个不连续的阶梯函数,可以用来检验算法的有效性:

全局最优点xi=0,f(x)=0.不连续阶梯函数的适应度收敛曲线对比结果如图7所示,可以看出MSO和FA的收敛速度最快.

图7 11种算法在不连续阶梯测试函数中的适应度函数收敛曲线对比Fig.7 Contrast of convergence curves of fitness functions of eleven algorithms in discontinuous step test functions

Rastrigin 函数是多峰函数,可以用来检验算法跳出局部最优能力:

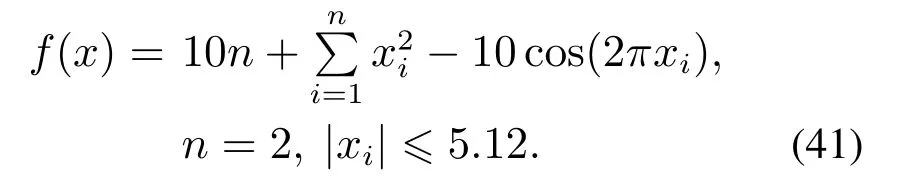
全局最优点xi=0,f(x)=0.不连续阶梯函数的适应度收敛曲线对比结果如图8所示,可以看出MSO的全局寻优能力体现较为明显,其他对比算法都不同程度地陷入局部最优点.

图8 11种算法在多峰测试函数中的适应度函数收敛曲线对比Fig.8 Contrast of convergence curves of fitness functions of eleven algorithms in multimodal test functions

4.2 仿真模型

本系统含有27台机组包含13台燃油机组并且都考虑了阀点效应、4台热电联产机组、4台只供热机组、3台风电机组、3台光伏机组.对于燃油机组、热电联产机组、供热机组来说,其数据分别如表2–4,热电联产机组的可行运行区域如图9所示[33].对于风电机组来说,风力发电机组的容量分别为130 MW,94 MW和94 MW;形状参数k为2,尺度参数c为15;切入风速为15 m/s,额定风速为5 m/s,切出风速为45 m/s[23];对于光伏机组来说,光伏电站的光伏列阵总面积为80000 m2,光电转换效率为14%,最大光照强度为700 W/m2;形状参数为0.95,尺度参数为0.95[23].

风力机组直接成本系数为120$/MWh、低估成本系数为15$/MWh、高估成本系数为20$/MWh.光伏机组的直接成本系数为200$/MWh、低估成本系数为15$/MWh、高估成本系数为20$/MWh[23].总的电力需求、热需求分别为3837.136 MW,615.372 MW[23].所有的网络损耗均被忽略掉.为兼顾算法最佳性能、计算速度和公平性,迭代步数设置为300.

表2 仅发电系统参数Table 2 Parameters of thermal units

表3 热电联产系统参数Table 3 Parameters of CHP units

表4 仅产热系统参数Table 4 Parameters of heat-only units

图9 热电联产装置运行区域Fig.9 Feasible operation region of the CHP unit

4.3 结果分析

图10代表了各种算法分别运行10次的盒须图,从盒须图对比中可以发现MSO收敛稳定性不如GA和GWO,但是其变化范围仍然是在可以接受的,且优化效果要好于GA和GWO.

为了验证MSO的速度,图11给出各种算法分别运行10次得到的平均运算时间对比条形图.从对比图中可以看出,MSO算法的计算时间用时最少,比SA算法快了接近4.96倍,能够很好地满足时间上要求.

图12、表5和表6给出了不同算法适应度函数的收敛情况和优化结果对比,其中:Power代表机组类型为仅发电的燃气机组;CHP代表热电联产机组;Heat代表仅发热的热机组;WT 代表风力发电机组;PV代表光伏发电机组.从最后优化的结果可以看出,MSO得到的适应度函数值最小,从而可以验证MSO算法能够跳出局部最优的缺点,具有很好的全局寻优能力.并且由图可得MSO从114代就开始收敛,极大提高了优化效率.