冷链物流越库调度的拉格朗日松弛算法

周炳海,宗 师

(同济大学机械与能源工程学院,上海 201804)

1 引言

越库(cross-docking)是一种物流策略,旨在使货物在供应链中快速的运输和分拣.越库也是一种仓储策略,目的是减少或消除仓储,从而降低供应链的成本.越库这一策略现已经广泛地应用于零售、制造等各个行业.

多年来,越库调度问题引起了国内外学者的关注,并针对不同的应用场景进行了深入的研究.Nassief等[1]研究了带有临时存储区域的越库门分配问题(cross-dock assignment problems,CDAPs),给出了两个整数规划模型,并对模型参数进行了灵敏度分析.Yin等[2]考虑了绿色环保的越库调度问题,在越库模型中增添了二氧化碳浓度的约束,并提出一种新的记忆人工蜂群算法进行求解.Karimi等[3]研究了越库网络在伊朗邮政系统内的应用,通过设置邮件的预设到达时间以控制和提高整个邮政系统的送件速度.Serrano等[4]考虑在雷诺汽车供应链的越库内部加入包装车间,实现了运输和加工同时进行的需求.Nassief 等[5]采用了拉格朗日松弛算法研究越库调度问题,但是仅研究了卡车到门的分配,未考虑卡车的排序问题.上述文献研究了越库在各类不同供应链或物流中的应用,其研究成果为接下来越库调度问题的研究提供了很好的参考和借鉴.

冷链物流作为一种特殊的物流方式,其最大的技术难点在于严格的时间和低温控制.冷链物流强调货物运输过程中的全局控制,如果有环节出现“断链”,即货物温度高于其最高贮藏温度,就会影响到产品质量与安全,使得整个供应链的可靠性大大降低.此外,高昂的冷库存储成本也阻碍着冷链物流的应用和发展.许多学者和企业也一直在寻找一种针对冷链物流的及时且高效的运作方法.越库调度策略在物流系统中具有及时性、高效性、低成本的特点,越库作为供应链上的中转站和连接点大大提升了物流效率,降低了仓储成本.因此,将越库调度策略运用到冷链物流中,一方面,减少了冷库存储需求,大大降低了成本;另一方面,越库使得货物具有了快速被分拣并装载的能力,货物暴露在常温下的时间大大降低,减少了“断链”的风险.

针对冷链物流的特点,提出了越库内的货物时间窗口,要求每种货物在规定的时间内通过越库[6].此外为了贴合实际应用,考虑设置越库门前临时存储区域,内设冷库,并分别给定不同的存储容量.基于越库的基本运作原理和冷链物流的特殊要求,提出了冷链物流越库调度的数学模型,并采用拉格朗日松弛算法,根据决策变量松弛复杂约束,提高模型求解速度和稳定性[7].

2 数学建模

2.1 问题描述

研究的越库配送调度主要包含3个部分,示意图见图1.

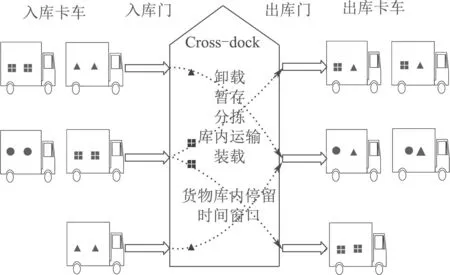
图1 冷链物流中的越库调度问题Fig.1 Cross-dock scheduling problem in cold-chain logistics

图1中:1)入库卡车到越库门的分配和入库卡车的排序:将装载着货物的入库卡车分别分配至一入库门,并对分配到同一入库门的卡车进行排序,按照排序进入越库.2)货物的库内运输:入库卡车进入越库后,将货物卸载于入库门前的临时存储区域,然后立即将货物运输至为其分配的出库门,暂存在出库门的临时存储区域内等待装载.此阶段考虑冷链物流中,每个货物在库内的时间窗口约束,根据不同的货物种类,要求货物在规定的时间内完成库内运输.3)出库卡车到越库门的分配和出库卡车的排序:将出库卡车分别分配至一出库门,并对分配到同一出库门的卡车进行排序,按照排序进入越库,装货后离开越库[8].

2.2 数学模型

基于上述的问题描述,建立如下数学模型:

1)模型假设.

①每个越库门在同一时间只能服务于一辆运输卡车;②货物在越库内部运输时,越库门距离越远,运输时间越长;③将货物分为k个种类,每个种类的货物对应于一个时间窗口约束tk,每种货物从入库到出库必须要在此时间窗口约束内完成;④临时存储区域设有冷库,可保证货物在低温下的存储.同时,每个临时存储区域设有容量限制,区域内货物之和不得超出此容量限制.

2)参数.

k ∈P为货物的种类;i ∈I为入库门编号;j ∈J为出库门编号;m ∈M为入库卡车编号;n ∈N为出库卡车编号;ULT为一辆入库卡车的卸货时间;LT为一辆出库卡车的装货时间;wk为货物k的数量;sm为入库卡车m装载的货物数量;rn为出库卡车n装载的货物数量;Si为入库门i前的临时存储区域容量;Rj为出库门j前的临时存储区域容量;dij为入库门i到出库门j的运输时间成本;tk为货物k在越库内部运输的时间窗口.

3)决策变量.

zkij:0～1变量,表示货物k是否由入库门i卸载并发往出库门j装载;xmi:0～1变量,表示入库卡车m是否被分配到入库门i进行卸货;ynj:0～1变量,表示出库卡车n是否被分配到出库门j进行卸货;pmn,qmn:0～1变量,表示入(出)库卡车m在卡车入(出)库排序中是否排在入(出)库卡车n的前面;Pm,Qn:整数变量,表示卡车在卡车入(出)库排序中的位次;Cm:整数变量,表示入库卡车m进入越库进行卸货的时间;Ln:整数变量,表示出库卡车n装货完成后离开越库的时间.

根据上述问题描述、模型假设、参数以及决策变量,对所研究的越库模型建模如下:

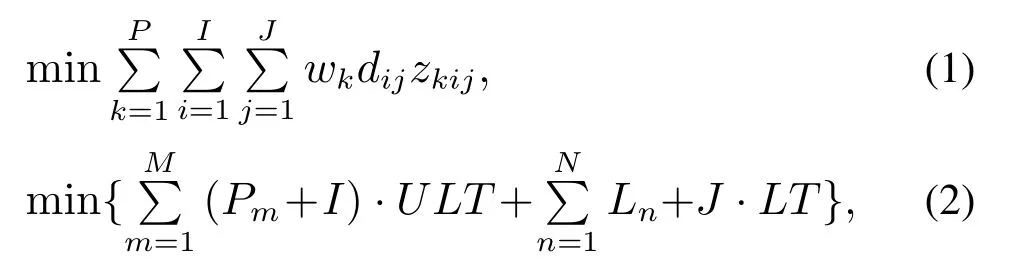
上述模型中,目标函数(1)是库内运输成本之和;目标函数(2)是卡车等待时间之和;约束(3)表明每种货物只能且必须被分配给一个入库门和一个出库门;约束(4)–(7)表明每辆卡车只能且必须分配给一个越库门;约束(8)–(11)给定了每个越库门前临时存储区域的容量限制;约束(12)表明每一种货物k在库内运输时与其对应的时间窗口;约束(13)–(16)表明卡车在越库门前等待队列中相互的先后顺序;约束(17)–(18)表明了每辆卡车在越库门前等待队列中的位次;约束(19)为入库卡车的入库卸货时间;约束(20)表明了入库卡车的卸货时间与出库卡车的装货时间的关系;约束(21)为出库卡车装货时间的先后关系;约束(22)为0～1变量约束.

3 拉格朗日松弛算法

3.1 松弛约束

将原模型中的约束(4)–(5)和约束(10)–(11)松弛到目标函数(1)中,引入拉格朗日乘子µ,ν,λ和γ,形成如下的松弛问题:

将原模型中的约束(19)松弛到目标函数(2)中,引入拉格朗日乘子η,形成如下的松弛问题:

拉格朗日对偶问题可表示为

3.2 求解子问题

根据拉格朗日分解思想,可将L(µ,ν,λ,γ)和L(η)根据不同的决策变量分解成多个子问题:1)关于决策变量z的子问题Lz(µ,ν,λ,γ);2)关于决策变量x的子问题Lx(ν,λ);3)关于决策变量y的子问题Ly(ν,γ);4)关于决策变量Pm的子问题Lp(η);5)关于决策变量Ln的子问题Lq(η)[9].

1)求解子问题Lz(µ,ν,λ,γ).

Lz(µ,ν,λ,γ)为关于决策变量z的子问题,是货物在越库内部运输路线的分配问题,可以被分解为基于货物种类k的独立子问题

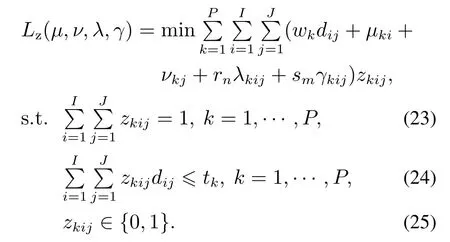
基于决策变量约束(23)和货物的时间窗口约束(24),求解出子问题Lz,从而得到货物k在越库中的由入库门到出库门的移动路线.

2)求解子问题Lx(µ,λ)和Ly(ν,γ).

Lx为关于决策变量x的子问题,是入库卡车到入库门的分配问题,可以被分解为基于入库门i的独立子问题

同理,Ly为关于决策变量y的子问题,是出库卡车到出库门的分配问题,可以被分解为基于出库门j的独立子问题

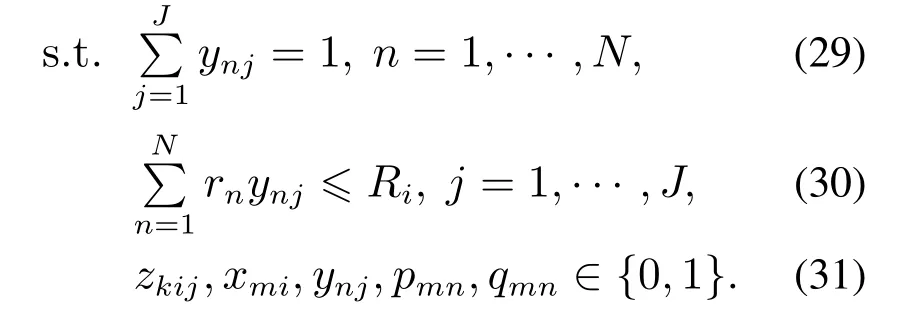
求解出子问题Lx和Ly得到卡车到越库门的分配情况.

3)求解子问题Lp(η)和Lq(η).

将求解子问题Lx(µ,λ)和Ly(ν,γ)得到的xmi和ynj代入式(32)–(33),即

其中:m,m′=1,···,M,m≠=m′,n,n′=1,···,M,n≠n′.然后进行车辆排序问题的求解,即求解子问题Lp(η)和Lq(η).

Lp(η)为关于决策变量Pm的子问题是入库卡车在每一个入库门的排序问题:

其中m,m′=1,···,M,m≠m′.

Lq(η)为关于决策变量Ln的子问题是出库卡车在每一个出库门的排序问题:

求解出子问题Lp(η)和Lq(η)得到卡车在越库门的排序.

3.3 次梯度算法

引入次梯度算法来求解拉格朗日对偶问题,每次迭代过程中根据如下公式进行拉格朗日乘子更新:

是货物在越库内部的运输成本,而目标函数(2)

是卡车在越库门的等待时间.对两个目标函数进行无量纲化处理并加权相加,得到一个统一的目标函数[10]

3.4 构造可行解

上述拉格朗日松弛的过程在大多数情况下得到的是目标函数的下界及其对应的不可行解.现采用拉格朗日启发式算法,对上述传统的拉格朗日算法进行改进,获得可行解.

拉格朗日启发式算法共包含两个过程:第1步,如上述过程采用次梯度法进行优化迭代计算;第2步,采用系数修正法对第一步得到的解进行可行化.系数修正法是拉格朗日启发式算法的一种形式,用于检验用次梯度法求解的当前解是否满足各条被松弛的约束.若存在未被满足的松弛约束,则选取出其对应的目标函数系数中的最小值di,并更新其对应的拉格朗日λ(t+1)=λt+di,直到此条约束被满足.直到当所有的约束(无论是否被松弛)都被满足时,则当前解为可行解.

3.5 拉格朗日松弛算法流程

步骤1初始化,令当前迭代次数t=0,令所有拉格朗日乘子为0;

步骤2求解每个子问题,目标函数值加权相加,得到下界;

步骤3对松弛问题的解通过系数修正法进行可行化;

步骤4判断是否符合次梯度法的停止准则,若符合则算法停止,否则继续;

步骤5进行拉格朗日乘子更新,返回步骤2[11].

4 实验与分析

本实验结果通过以下数据进行衡量:1)每一组数据运算的CPU时间;2)对偶间隙(%gap):

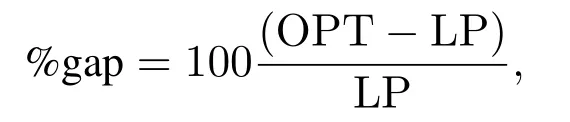
其中LP是每组实验通过拉格朗日松弛算法得到的目标函数值下界,OPT是根据系数修正法得到的可行解;3)对比算法的偏移(%dev):

其中UB是每一组实验数据通过贪婪算法得到的目标函数值上界.通过可行解和下界、上界比较得到了对偶间隙(%gap)和对比算法的偏移(%dev),这两个参数是拉格朗日松弛算法重要的评价指标,反映了可行解的优良程度和当前算法的可靠性.设定最大迭代次数为500,次梯度优化算法中取参数β=2[12].

本实验测试了所提出的拉格朗日松弛算法求解各种不同规模越库调度问题的性能.问题实例数据取值如下:卡车数量M,N=5,6,7,8,9,10,11,12,15;货物数量P=3,4,5,6;每种货物的数量wk在[200,500]间随机生成;临时存储区域的总量

其中:α分别取0.1,0.15,0.2,0.3;库内运输成本

每种货物k的库内运输时间窗口在库内最长运输时间的60%～100%间离散均匀分布产生.对于每种车–门数量组合,根据临时存储区域总量宽放α产生3–4种实验实例,一共产生49组实验.

原模型内双目标分别为库内运输成本之和以及卡车等待时间之和,两个目标数值差异较大,对最终结果的影响程度也相差较大.本实验用无量纲化加权的方法,将原模型内的双目标转换为单目标.经过多次实验,取b=0.95,此时统一的目标函数为

此时两个目标的数值接近,对模型的影响程度相近.以问题1为例,经多次迭代,库内运输成本之和为11520,卡车等待时间之和为741,采用b=0.95的加权方法后两目标函数分别为576和704,符合预期.

采用贪婪算法作为对比算法:一方面通过贪婪算法得到每组实验目标函数的初始上界;另一方面与通过拉格朗日松弛算法得到的近优解进行对比,判断解的质量.对比贪婪算法思路如下:将每辆卡车的货物由多至少进行排列,按照此顺序依次进入越库,每辆卡车在入库时选取当前库门剩余临时存储区域最大的入库门进入;入库后,依然按照上述排列顺序依次出库,每辆出库卡车依次选取当前库门剩余临时存储区域最大的出库门.

算法采用以下计算机配置进行实现:CPU:1.6 GHz Intel Core i5;内存:4 GB;电脑系统:Windows 7;编程语言:MATLAB.

实验结果如表1所示.

表1 不同规模问题的拉格朗日松弛算法与贪婪算法的结果对比Table 1 Comparison of Lagrangian relaxation algorithm and greedy algorithm of different scale problems

从表1可以得出如下结论:

1)大多数情况下,对于每一对车–门数量组合,随着临时存储区域宽放的增加,对偶间隙(%gap)会降低.因为临时存储区域总量增加后,对卡车入库的货物容量约束会降低,货物入库的条件得以放松,因此解的质量会有所提高;

2)大多数情况下,当卡车数量不变,库门数量增加时,对偶间隙(%gap)会降低.因为此时,分配到每个门的卡车数量相对减少,卡车可停靠的库门资源相对增加,卡车的排序问题相对简化,因此解的质量也会有所提高;

3)随着实验实例的规模增加,目标函数上界值(即对比贪婪算法的目标函数值)相较于目标函数近优解的偏移(%dev)越来越大.因此随着实验规模的增加,可行解数量的增多,拉格朗日松弛算法的优势逐渐显现,其解的质量相对于贪婪算法愈发优良;

4)本实验所有实例的平均对偶间隙和平均CPU时间分别为5.74%和990.67 s.因此,拉格朗日松弛算法能够在合理的时间内得到较为满意的目标函数下界和近优可行解.

5 结论

针对以冷链物流为背景的越库调度问题,考虑到实际运输过程中货物的冷藏条件,提出了带有货物时间窗口约束的越库调度问题,并对该问题进行描述,以最小化库内运输成本和卡车排序等待时间为目标,建立数学模型.继而采用了拉格朗日松弛算法,根据重要的决策变量将原问题分解为五个子问题,并通过次梯度算法进行模型的求解.实验分析了不同规模的越库调度实例,并得到相应结论.结果表明,拉格朗日松弛算法能够在合理的时间内得到较为满意的目标函数下界和近优可行解.后续研究将考虑如何进一步的提升解的质量,并提高算法运行速度.