学生的错误给我的启发
2020-05-11邓双婷
邓双婷
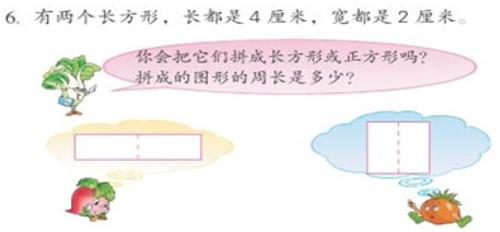

在教学三年级学生长方形、正方形周长的计算中,课堂练习有这么一道题如下图:
学生们通过动手操作拼组,拼成了两种不同的图形,如上图(下),大部分学生都通过观察,找到新拼的长方形的长和宽,然后根据周长的意义进行计算。在反馈中我发现学生都完成得比较好。
但有几个学生的做法及解释如下:先计算一个长方形的周长:4+2=6(cm)6×2=12(cm)。因为新图形是由两个相同的长方形拼接而已,所以得出新图形的周长是两个长方形的周长的和,即12×2=24(cm)。拼接的两个不同的新图形,它们都是由两个完全相同的长方形拼接而成,所以拼接的两个不同的新图形的周长相等,都是24cm,针对学生的错误,一方面,我引导学生描出新图形的周长,让学生感悟周长的意义,认识造成错误的原因是没有理解新图形的周长。并能够按照计算周长原始的方法正确地计算2+2=4(cm)。4×4=16(cm)或4+4=8(cm)8+2=10(cm)10×2=20(cm)。另一方面,学生的错误给了我为学生创设问题的启发,我提出了几个问题:(1)能不能用这种方式解决这个问题?(2)怎么解决?同时引导学生们再次动手拼接操作,带着问题去观察。在拼接过程中,再次引导学生思考:新图形比原来的两个长方形少了什么?少了几条长或宽?学生在回答问题时,我利用自己制作的简单的课件,加以演示。让学生们清楚地知道,新图形周长比原来的两个长方形的周长少了两条长或两条宽,新图形的周长是24-4×2=16(cm)或24-2×2=20(cm)。
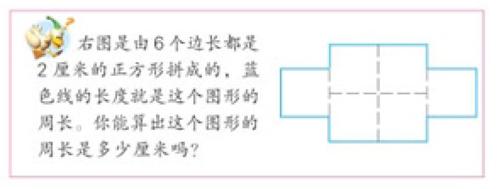
用这种方法解决本题,虽然没有很多的优势,但这种解题思想,去解决其它的问题就迎刃而解。如课堂练习中的思考题如下:
本题可以用平移成规范的长方形再计算。也可以先计算6个小正方形周长和:6×2×4=48(cm),再观察数出重叠的小正方形边数,从中减去就是。48-12×2=24(cm)。也可以将重叠的边数折合成小正方形周长的个数,直接算出。即:3×2×4=24(cm)。这种解题思想,为高年级表面积的计算打下了良好的基础,如左下图:
有了低年级的这种思想方法,高年级的学习能够马上体会到:可以用6个正方体的表面之和减去重叠的几个面的面积。要解决哪个立体图形的表面面积大这个问题,就看哪个立体图形减少的面少,表面积就大,这样复杂问题就简单化了。
思维灵活的学生用这种方法,举一反三解决下面的难题:
例1:4个周长17厘米的长方形拼成一个大的长方形,如左图:求大长方形的周长。
解题思路是:拼成大长方形后减少了4条长和4条宽,即减少了两个长方形,所以只能算2个长方形的周长和:即17×2 =34(cm)
例2:将一张边长45厘米的正方形剪成4个完全一样的小正方形纸片,问这4个小正方形周长的和比原来的正方形周长增加了多少厘米?
解题思路是:只要将问题转化为增加了几条正方形的边,再转化为增加了几个正方形的周长,即45×2=90(cm)
“错误常常是正确的先导。”只要我们注意经常引导学生去分析总结解题中出现的错误,并利用这些错误,积极改进教学方法,就能达到增加兴趣,啟迪思维,培养能力,更好地预防差错、纠正差错的目的。
