整体观指导下的初中函数单元总复习实践研究

丁福珍

(浙江省天台县教育局教研室 317200)

复习课的教育价值是建立系统和简约的知识体系，提炼数学的思想和方法，积累数学活动经验，并把得到的数学知识、思想方法和活动经验迁移应用，在此过程中提升学生的数学素养.也就是说，复习课要帮助学生在知识的结果性认知基础上，建构知识之间的关系网络，使本单元知识、相关单元知识之间建立起具有简约性、多触点、结构化的系统[1]；在理解数学知识的本质、建立相关知识的联系中，概括数学思想和方法；在应用知识解决问题的过程中，积累数学活动经验，发展数学素养.

当前，初中复习教学普遍存在知识碎片化现象，课堂上尽可能多地讲题型，再进行“无死角的知识点覆盖”训练.这种复习存在两个突出问题：第一，没有对知识形成联系性的认识，导致对知识缺乏系统的整体理解，细碎的重复训练加重了学生的课业负担；第二，缺乏数学思想与方法的指导，生搬硬套的题型训练导致思维僵化，学生只会机械地模仿解题，导致独立思考、灵活运用知识解决问题的能力低下，难以积累有效的数学基本活动经验.

那么，怎样的复习教学才能使学生在认知重构过程中落实“四基”、发展“四能”呢？本文以“一次函数、二次函数和反比例函数”复习教学为例，谈谈整体复习教学的实践与思考.

1 内容分析

1.1 地位与作用

函数是中学数学的核心内容，是联系数学不同分支的桥梁和纽带，是研究变化过程的重要数学模型.初中阶段学习一次函数、二次函数、反比例函数，借助图象直观研究函数性质(图象的特征和函数的增减性).这三类函数对高中阶段的函数学习起到奠基作用.

1.2 主要的思想和方法

每一类函数概念的抽象过程中蕴含着抽象思想；借助图象研究函数性质的过程中蕴含着数形结合思想；观察图象、探索性质过程中的抽象思想；根据参数取值范围讨论函数性质的分类思想；研究一类函数的基本套路.

1.3 关键能力

整理知识，构建体系，概括思想方法及研究套路过程中的数学抽象能力；建立函数模型刻画变化过程的数学建模能力；利用函数性质分析变化过程中的逻辑推理能力；借助图象理解变量之间关系的直观想象能力.

1.4 教学重点

整理三类函数的知识结构，提炼建立函数模型解决问题的方法，概括函数研究的一般套路并能用这种套路研究一些简单的新函数.

2 教学策略

采用整体建构教学策略[2]：在一般观念指导下，对三类函数进行整合复习.首先，引导学生分别回顾一次函数、二次函数、反比例函数的定义、图象和性质以及它们的研究思路、研究内容和研究方法；其次，在回顾的基础上进一步概括这三种函数的定义、图象、性质的共性和区别，对“函数图象用来做什么”、“函数性质指什么”这些问题进行一般性的回答，帮助学生理解函数图象及性质的本质；第三，分析这三种函数的研究思路、研究的内容和研究方法，概括出它们的共性，形成研究的基本套路及思想方法的一般性理解，积累数学活动经验；最后，用概括出的这种一般观念指导新函数的研究，实现思想方法、活动经验的迁移.在上述复习的基础上，设计专门的习题课，进一步研究函数、方程和不等式的关系，在更广阔的领域中构建知识之间的关联，体会函数的纽带作用，初步形成函数思想.

3 教学过程

将三类基本函数复习整合成两个课时，第一课时“一次函数、二次函数和反比例函数的图象和性质”，第二课时“一次函数、二次函数和反比例函数的图象和性质习题课”.本文只呈现第一课时的教学过程.

3.1 承上启下，提出问题

基于前一节课“变量与函数”的复习，回顾用函数模型研究变化过程的框架：

在此基础上，着重指出从定义出发研究函数的性质，对于一些典型变化过程的研究、变化规律的把握是至关重要的，从而提出本节课复习内容“一次函数、二次函数和反比例函数的图象和性质”.

3.2 类比思考，回顾三类函数的相关知识

首先，由老师引导学生回顾一次函数的研究思路、研究内容和研究方法，得到一次函数的相关知识.

研究思路：定义——图象——性质.

研究内容：图象特征(形状、位置)和性质(增减性).

研究方法：对k进行分类，画出具体函数的图象——观察发现——归纳推广.

一次函数的有关知识：

定义图象与特征性质一次函数y=kx+b(k≠0)y=kx+b (k>0)y=kx+b (k<0)k>0,图象过一、三象限k<0,图象过二、四象限k>0,y随x的增大而增大.k<0,y随x的增大而减小.

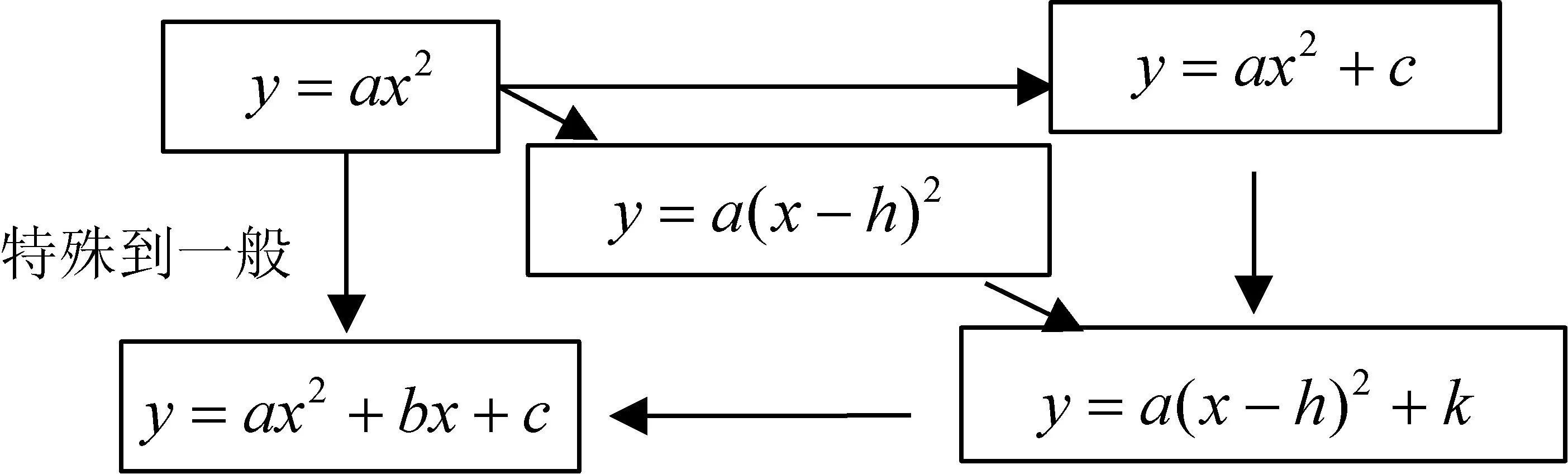
接着，让学生类比上述过程，独立回顾二次函数和反比例函数的研究思路、研究内容、研究方法和有关知识，并写出相关内容.例如，二次函数的相关内容如下：

研究思路: 定义——图象——性质.

研究内容：图象特征(形状、位置、对称性)和性质(增减性、最值).

研究方法：对a进行分类，画出具体函数的图象——观察发现——归纳推广.

二次函数的有关知识：

定义图象与特征性质二次函数y=ax2+bx+c(a≠0)y=ax2+bx+c (a>0)y=ax2+bx+c (a<0)a>0,开口向上,顶点最低.a<0,开口向下,顶点最高.a>0,对称轴的左侧,y随x的增大而减小,对称轴的右侧,y随x的增大而增大.a<0,对称轴的左侧,y随x的增大而增大,对称轴的右侧,y随x的增大而减小.

3.3 整理归纳，构建三类函数的知识体系和研究套路

引导学生说出三类函数模型的共性与差异性,整理知识结构如下表:

定义图象与特征性质一次函数y=kx+b (k>0)y=kx+b(k<0)k>0,图象过一、三象限k<0,图象过二、四象限k>0,y随x的增大而增大.k<0,y随x的增大而减小.二次函数y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)a>0,开口向上,顶点最低a<0,开口向下,顶点最高图象关于直线x=-b2a对称a>0,对称轴的左侧,y随x的增大而减小,对称轴的右侧,y随x的增大而增大.a<0,对称轴的左侧,y随x的增大而增大,对称轴的右侧,y随x的增大而减小.反比例函数y=kx (k>0)y=kx (k<0)k>0,图象过一、三象限k<0,图象过二、四象限图象关于原点对称k>0,在每个象限内,y随x的增大而减小.k<0, 在每个象限内,y随x的增大而增大.

让学生归纳三类函数的研究思路、研究内容和研究方法的共性：

研究思路:定义(给出函数解析式的特征)——图象——性质；从特殊到一般.

研究内容:图象的形状、位置和特征(线性与非线性、连续与不连续、对称性)；函数的性质(增减性、最值等)；图象用来直观地反映函数的性质，函数性质指的是当自变量的值增加时，函数值是增大还是减小，是按照什么规律(线性与非线性，是否有间断点，是否有最值，变化速度快慢等)变化的[1].

研究方法:从定义出发，画出具体函数的图象——观察发现——归纳推广；其中蕴含着数形结合和分类讨论的思想.

这种研究套路同样适用于其它函数的研究.

3.4 拓展提升，促进数学活动经验的迁移

学生尝试研究：分k>0和k<0两种情况.

(1)k>0时，研究特例:k=1，先研究b=0,b=1,b=-1的情况，分别画出图象(如图1)：

图1

归纳性质：当k>0时，图象是关于(-b,0)对称的两支双曲线，当x<-b时，y随着x的增大而减小，当x>-b时，y随着x的增大而减小.

(2)k<0时.研究特例:k=-1，再研究b=0,b=1,b=-1的情况，分别画出图象(如图2)：

图2

归纳性质：当k<0时，图象是关于(-b,0)对称的两支双曲线，当x<-b时，y随着x的增大而增大，当x>-b时，y随着x的增大而增大.

3.5 总结反思，将知识体系纳入长期记忆

让学生说说一次函数、二次函数和反比例函数的图象和性质的研究思路、研究内容、研究方法和相关知识，形成简约化的知识体系.

4 教学反思：价值取向

4.1 通过单元整体复习，构建系统简约的知识体系

单元整体复习是指依据学习内容的逻辑关系划分具有紧密联系的单元，进行单元整体教学设计，让学生自主建构知识体系，实现知识结构的重构[2].本节课把三类函数的图象和性质进行整体复习，通过分析比较，让学生在相互联系中进一步理解三类函数图象和性质的区别与联系：区别是指三类函数的变化模式不同；联系指的是三类函数的定义方式、性质所指、研究套路是相同的，即都是从现实背景中引入，都是根据解析式的特征加以定义的，性质指的是“当自变量的值增大时，函数值是变大还是变小，是按照什么规律变化的”，研究的套路都是相同的，只不过所研究的函数类型不同.这样做可以让学生从相互联系中深化知识的理解，掌握三类不同函数的变化趋势和变化规律及其适用的变化过程，便于学生在选择适当的函数模型研究变化过程中运用自如.

4.2 一般观念引领，注重从内容中提炼数学思想和方法

章建跃博士指出，一般观念指的是对内容及其反映的数学思想和方法的进一步提炼和概括，是对数学对象的定义方式、性质指什么、怎样研究等问题的一般性回答，是研究数学对象的方法论，对学生学会用数学的方式对事物进行观察、思考、分析以及发现和提出数学问题等都具有指路明灯的作用.本节课的教学中特别注意体现“一般观念”的指导作用，“回顾”阶段，创设类比情境，回顾三类函数的相关知识及研究套路；“整理”阶段，把三类函数的定义、图象、性质进行比较，理解这三种函数变化模式的区别与共性，从而对“一类函数是怎样定义的”“函数图象有什么用”、“函数性质指什么”等问题给出一般性的回答，在此基础上概括“一类函数是如何研究的，研究的思路、内容、方法分别是什么”.这样，通过分层次的概括，帮助学生理解函数性质的本质，形成研究的一般思路，提炼与内容融合的数形结合、分类讨论等思想方法，并明确这些思想方法是在哪些环节运用以及如何使用，从而有效积累数学活动经验.

4.3 设计挑战性问题，促进知识和经验的迁移

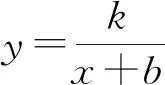
学生在这样的复习过程中，不只是知识的简单提取与套用，而是需要用已有的知识和经验研究新问题，从而形成有效的深度学习，保证了复习过程中数学思维的含金量；学生在这样的过程中获得的知识经验是可迁移的，所形成的是真正意义上的数学活动经验；学生在这样的过程中，可以结合知识理解的深入而深刻体会内容蕴含的数学思想与方法，形成研究问题的一般套路，并发展有逻辑、创造性的思考能力。所以，整体观指导下的单元复习是提升学生数学素养的有效举措.