利用“同构”法解决正方体展开图问题

江加乾

(北京一零一中学 100091)

数学与人类发展、社会进步息息相关，数学素养的提高是数学教育的着力点．本文从正方体展开图这一课例出发，对数学素养的培养进行一些思考．

有些立体图形是由一些平面图形围成的，将它们的表面适当剪开，可以展开成平面图形．这样的平面图形称为相应立体图形的展开图．[1]

从认知心理学方面来说，心理学家们致力于研究我们是如何进行推理、问题解决和决策的．其中的“问题解决”是指将现有信息与头脑中储存的信息结合起来解决问题的行为．在人工智能方面做出突出贡献而获得图灵奖的美国学者纽厄尔和西蒙，将问题分为初始状态、目标状态和问题处理三个阶段．提出在问题解决策略中，可以采取一系列方法，尤其是算法，来最终获得问题的解决[2]．心理学中的算法是指为了获得问题的解决而一步一步执行的程序．算法可以是一些公式和程序，在正确使用的情况下，总是能够奏效的．因为这是“按部就班地遵循了直接把问题引向答案的程序”[3]．借助于算法，在某一类相似的问题中，我们不但能够让我们的大脑来采取相似的“程序”来解决问题，甚至还可以利用计算机程序来实现算法进而解决问题．在研究正方体的展开图这一具体问题中，我们从展开图的结构出发，探索展开图之间的联系，尝试应用算法思想，探索“程序化”的方法，让静态的展开图“动”起来，获得解决问题的新角度，进而在探究过程中，培养学生的几何素养．

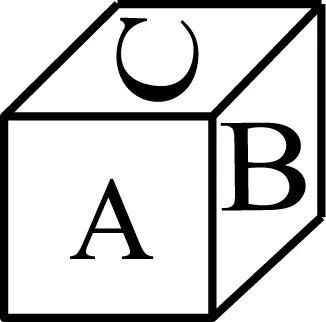
将右边的正方体展开，能得到的图形是 ( ) .

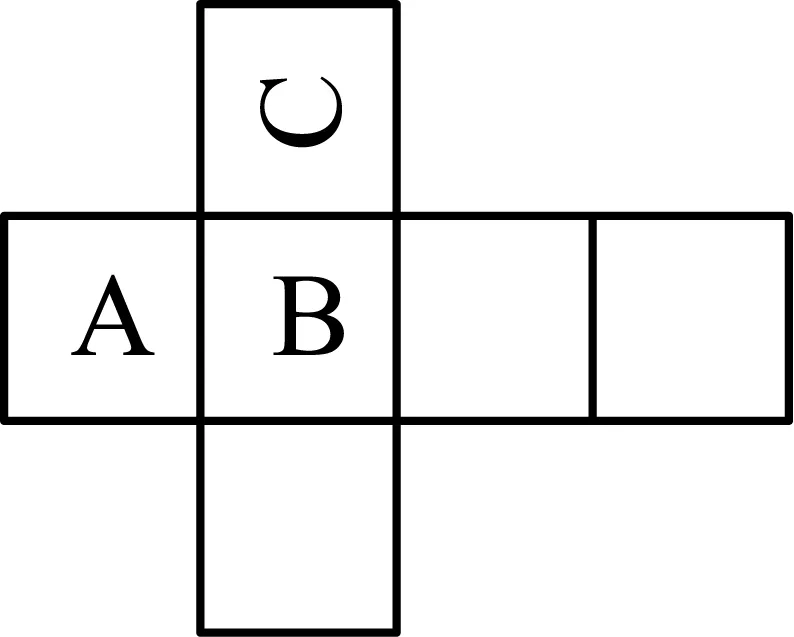
A

B

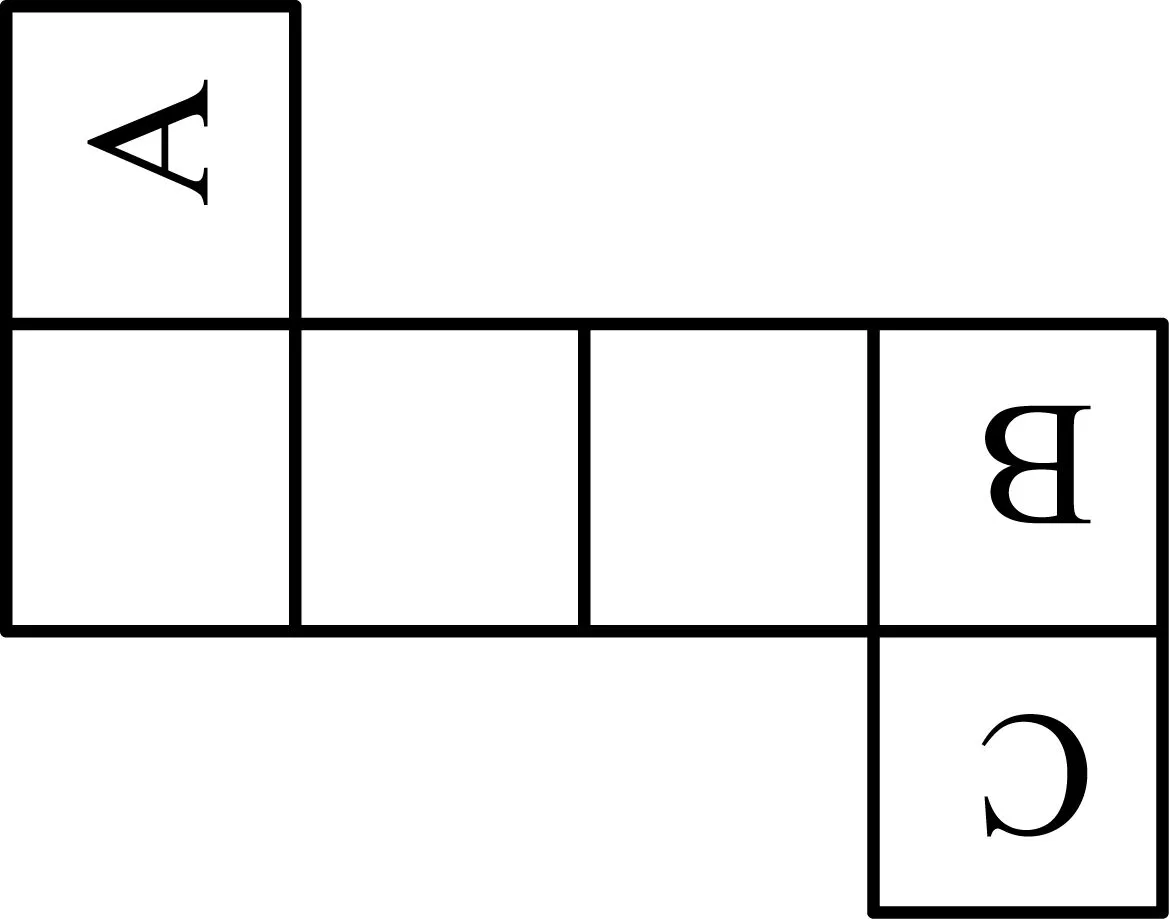
C

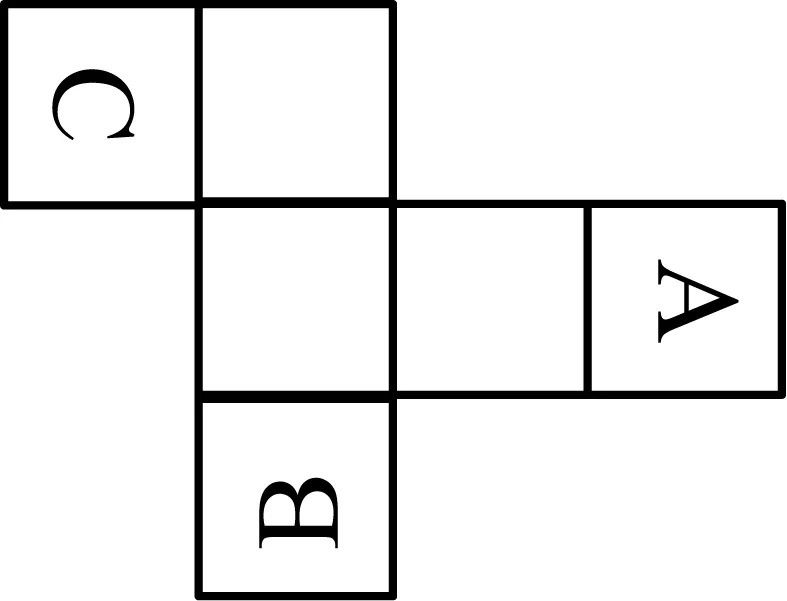
D

问题分析：

我们把正方体中有公共顶点(记为M)的三个面的三条棱剪开一条后展开，其结果对应于图1～3所示的图形之一，要注意图形里三个面的字母是有方向的．

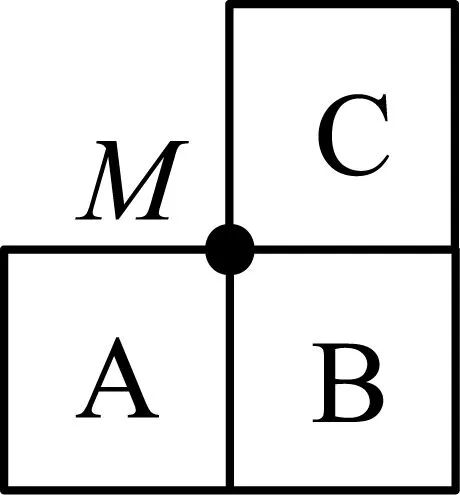
图1

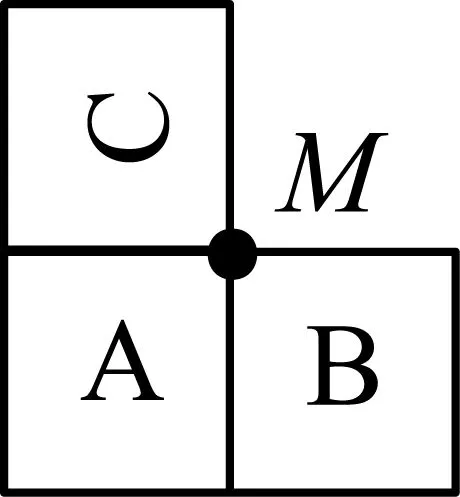
图2

图3

这三个图形之间有什么联系呢？

把图1的正方形C绕公共顶点M逆时针旋转90°可以得到图2，把图2中的正方形B绕公共顶点M逆时针旋转90°可以得到图3，把图3中的正方形A绕公共顶点M逆时针旋转90°再整体顺时针旋转90°就可以得到图1．这三步操作都是可逆的．虽然这些图形不同，但它们都是同一个正方体的组成部分，笔者把这些图形称为“同构图形”．

这样，我们发现: 如果正方体展开图中有三个面是共顶点的，那么其中有两个面可以绕公共顶点旋转90°到新的位置，这样就得到新的展开图，新、旧展开图都可以折叠成同一个正方体，它们是“同构展开图”．

笔者把这种由旋转得到同构展开图的方法称为“同构”法．这一算法的初始条件是三个面共顶点的情况．步骤是将这三个面中的某一个面绕着公共顶点旋转．目标就是能够得到一些同构展开图．

需要注意以下两点．

第一，我们在利用同构法时，要判断初始条件．例如下图展示的两种旋转，图4是把正方形C绕着点N顺时针旋转90°，图5是把正方形C绕着点N顺时针旋转180°，这两种变换都不是使用同构法．因为不符合初始条件，从已有图形看来，点N不是某三个面的公共顶点．

图4

图5

第二，如果被旋转的正方形连接其它正方形，这些正方形可以一同跟着旋转，例如，下图使用同构法是把正方形A，B，C，D绕着正方形B，C，E的公共顶点P顺时针旋转90°从而得到新的同构展开图．

类似地，以下这些展开图都是同构的：

例：将右边的正方体展开，能得到的图形是 ( ) .

A

B

C

D

解法：选项A中，字母B的上方和字母C的左侧相对，而题干中字母B的上方和字母C的下方是相对的，不符合题意；

选项B中，展开图的字母比较分散，不容易判断，我们可以用同构法，把正方形A绕着点M逆时针旋转90°，我们看到，字母B的右侧和字母A的左侧相对，不符合题意；

选项C中，我们可以利用同构法，第一步把正方形A绕着点P顺时针旋转90°，第二步绕着点M顺时针旋转90°，第三步绕着点N顺时针旋转90°，得到同构展开图．

这样旋转三次，我们看到，字母A的上方和字母B的下方相对，不符合题意；

选项D中，我们利用同构法，第一步把正方形C绕着点P逆时针旋转90°，第二步把正方形C绕着点M逆时针旋转90°，第三步，把正方形A连同它左边的正方形一起绕着点N顺时针旋转90°，第四步，把正方形A绕着点R顺时针旋转90°，很显然，选项D符合题意．

下面我们再通过一些例子来看看同构法的应用．

例1． 如图6，在正方体的表面上画有斜线，图7是其展开图，但只在A面上画有斜线，那么将图6中剩余两个面中的斜线画入图7中，画法正确的是 ( ) .

图6

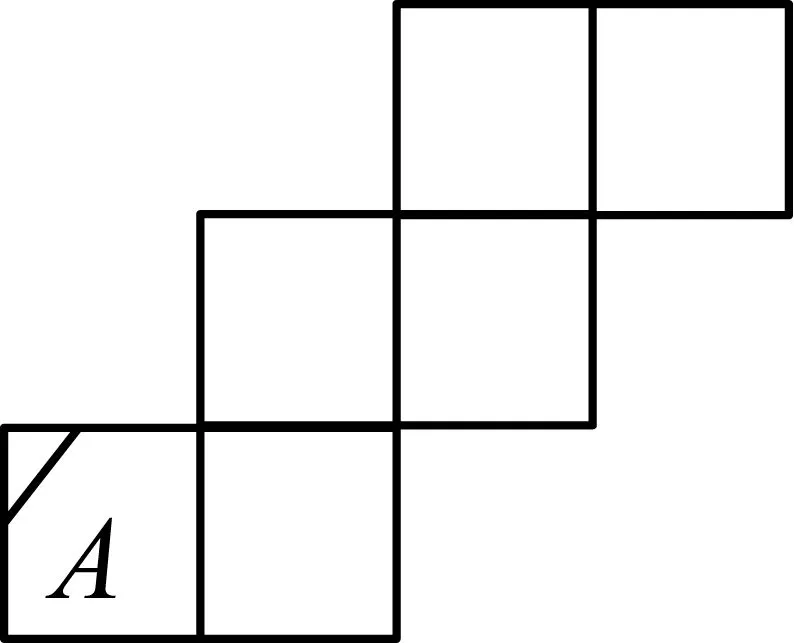
图7

A

B

C

D

解: 对于选项A中的展开图，我们可利用同构法依次进行如下变换:

图8

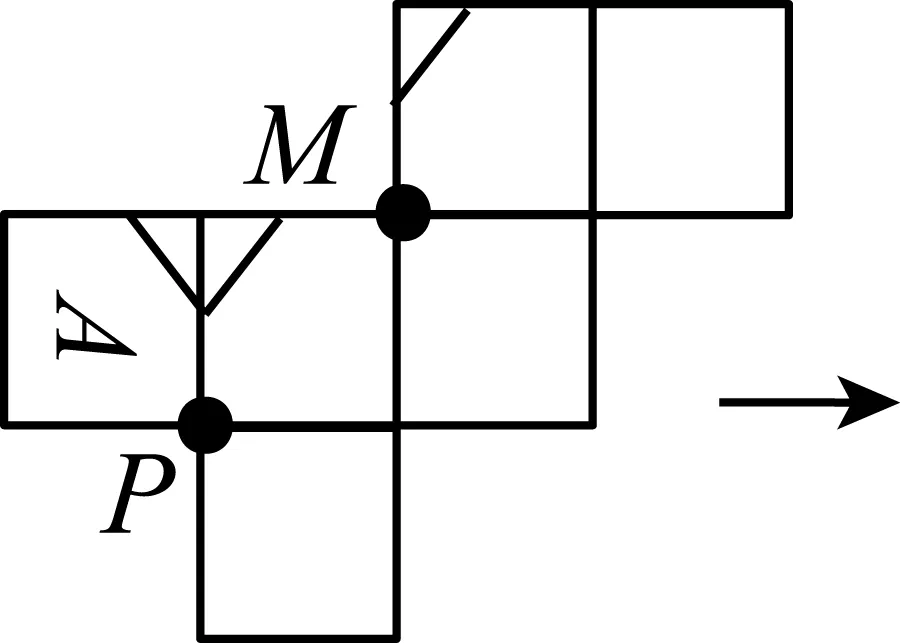
图9

图10

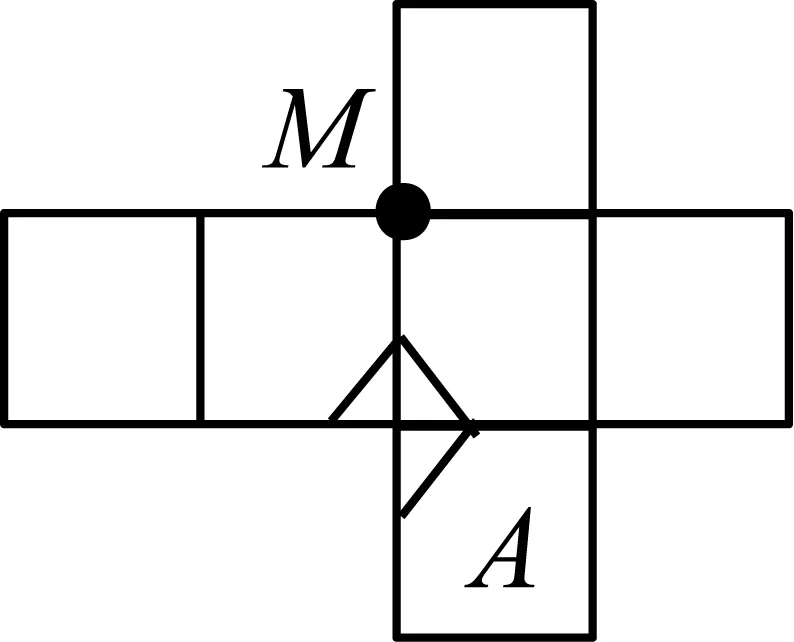
图11

首先把图8中的点P左下方的正方形绕着点P顺时针旋转90°，然后把图9中的点M右上方的正方形连同它右边的正方形一起绕着点M逆时针旋转90°，最后把图10整体逆时针旋转90°得到图11，容易看出图11符合题意，从而选项A是正确的．

例2． 右图表示一个正方体的展开图，下面四个正方体中只有一个符合要求，那么这个正方体是 ( ).

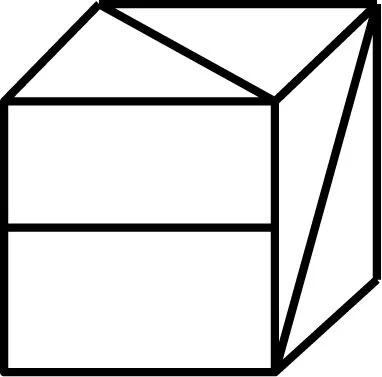
A

B

C

D

解: 因为选项C和D中空白侧面和带有横线的侧面是相邻的，这和它们本应是相对的面矛盾，因此排除选项C和D．

对于选项A，我们可依次把展开图进行如下同构变换:

图12

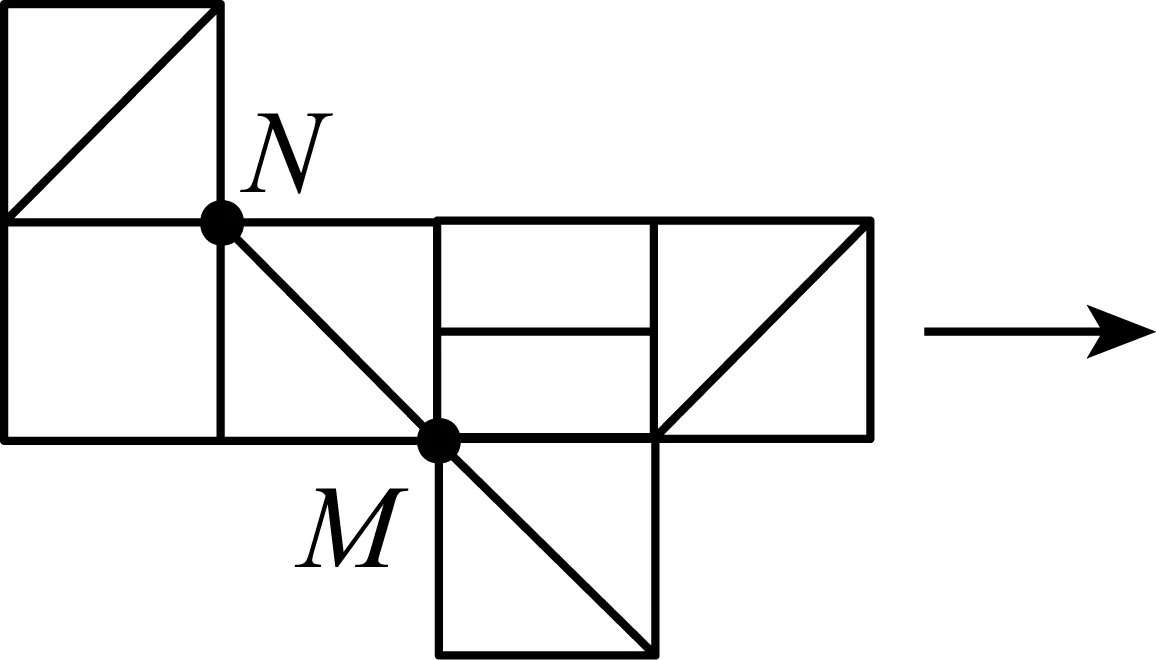
图13

图14

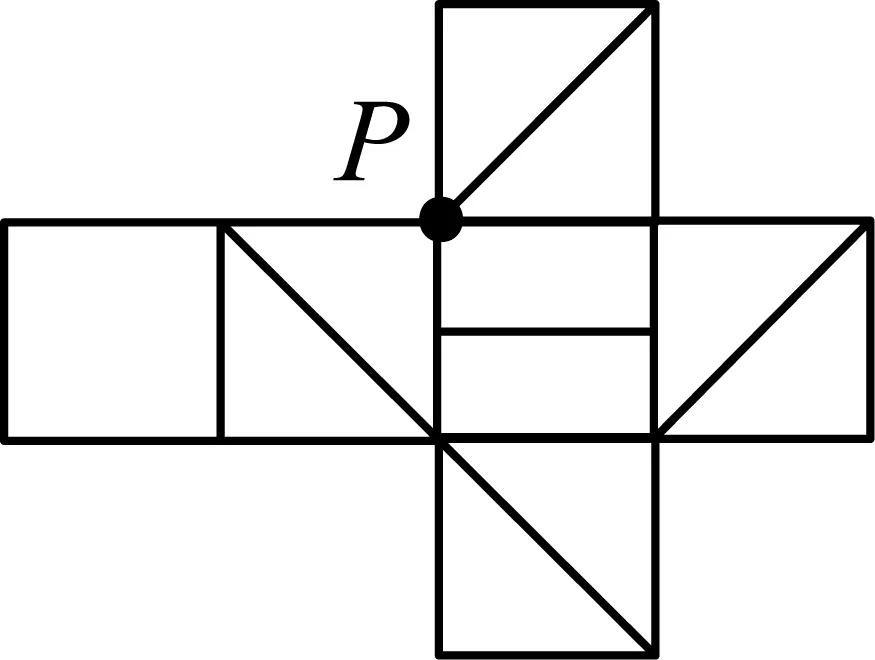
图15

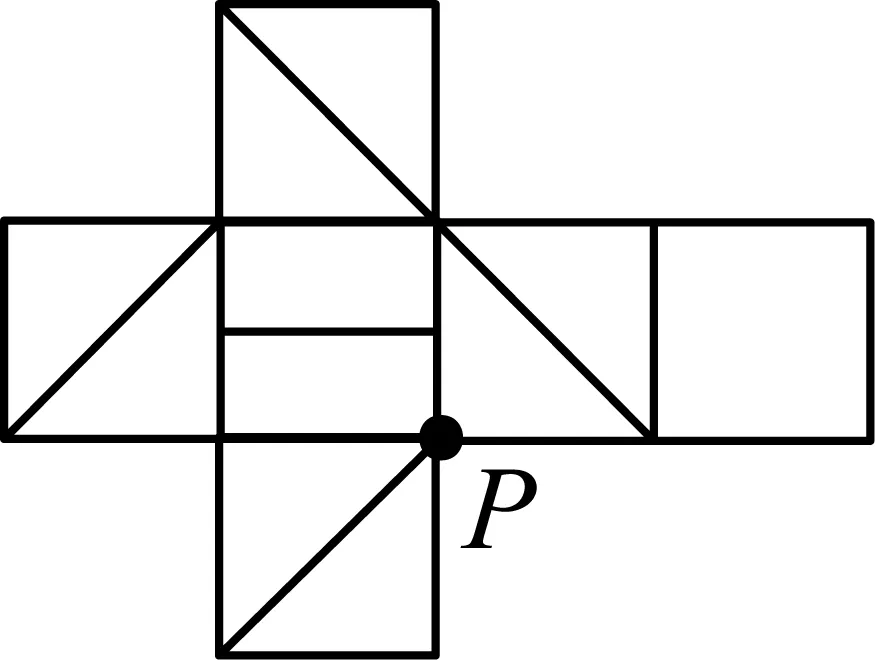
图16

首先把图12中的点M左下方的三个正方形，绕着点M顺时针旋转90°，再将图13中的点N左上方的正方形绕着点N顺时针旋转90°，再将图14中的点P左上方的正方形，绕着点P顺时针旋转90°，这时得到图15；再将图15整体旋转180°得到图16，这时发现图15和图16，均不符合A选项．

对于选项B，我们可以依次把展开图进行如下同构变换:

图17

图18

图19

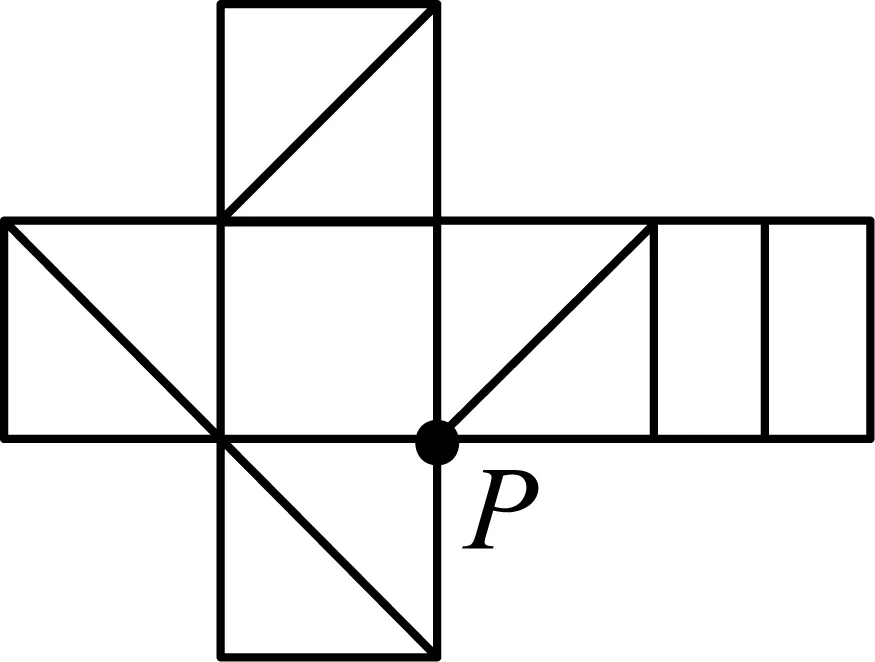
图20

图21

首先把图17中的点M右上方的三个正方形，绕着点M顺时针旋转90°，再将图18中的点N右下方的正方形，绕着点N顺时针旋转90°，再将图19中的点P右下方的正方形绕着点P顺时针旋转90°，得到图20；再将图20整体逆时针旋转90°得到图21，这时发现，图21是符合题意的．所以此题选择B．

通过上面的例子我们可以感受到，利用同构法，我们很容易得到一系列同构展开图，能够准确地解决正方体的展开图这类问题．

这一探索过程，对于我们的几何教学有一些启发．

首先，各课程的不同层次要进行区分．

古德莱德将课程分为五种：理想的课程，正式的课程，领悟的课程，运作的课程和经验的课程．就本文的呈现方式来说，开篇直接展示了教师领悟的课程，而在运作的课程中，应当逐步引导学生探索发现同构法，使之成为学生体验到的课程．学生在逐步的体验过程中，感受立体图形和平面图形的联系，在归纳同构法的过程中，提高学生的几何素养．

其次，问题解决为导向的研究方法可以适用在几何变换中．

代数式的变型和化归，常常要分析目标代数式与初始代数式之间的联系和桥梁．而在正方体展开图这一几何问题中，我们也可以用问题解决来指导我们的思路分析．我们将初始的展开图，经过一系列同构变换，得到与之同构的目标展开图，顺利解决了问题．由于同构法有明确的操作步骤，学生可以很快掌握，这样学生今后在解决这一类问题时更加顺利．

第三，结构性的知识归纳需要对空间想象能力进一步提升才能够形成．

教育学中结构性的知识是指规范的、具有内在逻辑的、抽象出来的基本原理和方法．同构法就是这样一种结构性知识，按照一定的规律操作，我们总能解决目标问题．这容易形成一个误区，即教师把结论教给学生就够了，学生容易自满于模仿．因此，尤其要强调，知识的归纳不仅仅是目的．探索总结出这样的结构性的知识，是在教师解决了一系列正方体展开图问题的基础上实现的．学生在使用该方法的过程中，也需要空间想象能力作为保障，并不是单纯的记忆和操作．该方法的归纳是空间想象能力提升的结果，同时也是空间想象能力的进一步强化．

最后，教师应在教学中多关注典型问题的教育价值．

从我们的数学教育课程方面来说，《普通高中数学课程标准(2017年版)》[4]中提出数学学科核心素养包括六个方面：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析．《义务教育数学课程标准(2011年版)》[5]提出要注重发展学生的“空间观念”、“几何直观”等．几何方面的直观想象与空间想象能力一直是数学素养的重要组成部分．对于初中的学生来说，正方体的展开图是学生在中学阶段接触的较早的平面几何与空间几何相结合的问题，非常有助于培养学生的几何素养．从教师的专业发展角度来说，需要平时多积累，关注数学素养各方面的典型问题，发掘这些问题的教育价值，不断提高教师自身的专业素养．