测量误差分析及数据处理若干要点系列论文(二)——随机性分布统示法综论

林洪桦

测量误差分析及数据处理若干要点系列论文(二)——随机性分布统示法综论

林洪桦

（北京理工大学，北京 100081）

阐述现代数据处理中随机性分布统示法必要性及表示方法，包括基于分布函数的理论方法、频率分布的近似方法、基于样本数据的直接方法等，并概述了各自特点及实用中应注意的问题；对误差分析及数据处理归结出基本观念、目标、依据、推论原则、处理方法等要点，结合统示法论述，并针对统示法进行选择。

数据处理；数学模型；误差；统示法

在文献[1]中，笔者已阐述了现代数据处理基本观念，包括数据处理目标、依据、实质、现实问题的性质和随机性分布，并根据数据处理对策，对现代数据处理归结出“实、佳、智、验”四字要诀。本文将进一步阐述现代数据处理中随机性分布统示法的必要性以及表示方法。

1 随机性分布统示法的必要性

数据处理实质只是对现实的模拟，以数学模型模拟样本数据及先验信息所体现出的现实总体规律性，故数据处理结果应能准确地模拟出最本质总体规律，更具体、准确地模拟出现实问题待求的某一总体特性。

现实问题均属非线性、非高斯、非平稳的“三非”问题，其中对非高斯问题的研究不及非线性、非平稳广泛与成果显著，如可线性化、平稳化简捷处理等。唯独现实的随机性分布不可简化，只能够准地模拟。可见，对于现实随机性变量不宜说为××理论概率分布（在概率论中有严格定义），只能说可按××分布处理或够准地模拟为××分布。

在现实问题中，高斯分布随机影响因素未必占大多数，而非高斯分布的随机影响却客观存在，并随处可见，且对非高斯分布随机影响的统计处理方法较高斯分布复杂又难处理。非高斯分布不仅在理论分析上较难，即使在统计处理的特征量分析上，也比高斯分布仅需前二阶矩要多，至少需多考虑表示偏态、峰态的三阶、四阶矩，甚至更高阶矩。随着计算机及最优化技术广泛应用，对非高斯分布随机影响的统计处理已可实现，并已研究出许多有效而实用的统计处理方法。以往之所以多按正态分布处理，主要依据中心极限定理及渐近性理论条件（现实中这样条件却未必成立），而更重要的还在于其简便实用。况且，需考虑到必然会存在某些重要的非高斯性先验影响因素。总之，宜建立非高斯性为常态，而高斯性仅为特例的观念。

因此，在误差分析及数据处理中，研究非高斯分布随机影响的实用性统计处理方法，不仅十分必要，且是亟待解决的现实问题及主要研究方向之一。多年研究表明：在非高斯性为常态的观念下，运用随机性分布统示法处理概率分布模式问题颇有见效。

2 随机性分布统示法的表示方法

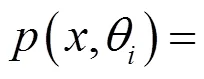
2.1 基于分布函数的理论方法

2.1.1 多参数分布族

早在19世纪末就已提出的理论分布函数族的统示方法（当时无此称呼），如Pearson分布族、Johnson分布族等。直到研究出蒙特卡罗（Monte Carlo, MC）方法、启发式算法、人工智能算法等可按样本数据进行分布函数拟合方法之后，基于分布函数的理论统示法才得以实际应用。

分布统示法：分布属PearsonⅠ型，直至20世纪中叶才出现按样本数据拟合分布函数的实用方法[3-4]，此后才逐步得以扩展应用。分布函数、特征量及其与参数关系及其对称性分布如表1所示。

关于分布，在此仅概述其特点及实际应用中需注意问题：

1）理论上是有界的，符合误差的有界性，不利于表述寿命、磨损等带拖尾形态的分布函数，只依据样本数据界限难以定准分布界限；

2）分布形态具有多态性，可呈对称分布、非对称分布、单峰分布、单谷分布、递增或递减分布等，可逼近各种常见的理论分布函数及实用误差分布，其覆盖面较大，难以表述多峰型分布；

3）具有一定的理论可解析性、实用的拟合方法，尤其当前可选用的智能算法颇多，宜选择具有全局优化性算法；当前仅利用前四阶矩，还未用到更高阶矩，特别要顾及分布界限的估计会受限于数据样本界限；还需强调，样本数据常不显示其对称性，而对称分布并不罕见，表1已显示出拟合对称分布更为简捷，可见经预作对称性识别后，宜按对称性优先原则处理[7]；

4）计算速度提升、存储加大以及运用专用软件等均有利于分布的应用，很有必要编制具有全局优化性且简捷的拟合分布通用软件；

5）按从特殊到特殊的转导型推理可知，估计出分布参数就可得到该分布的所有统计特性，无需去纠缠其是何理论分布。分布实际应用见文献[2,4-6]。

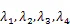
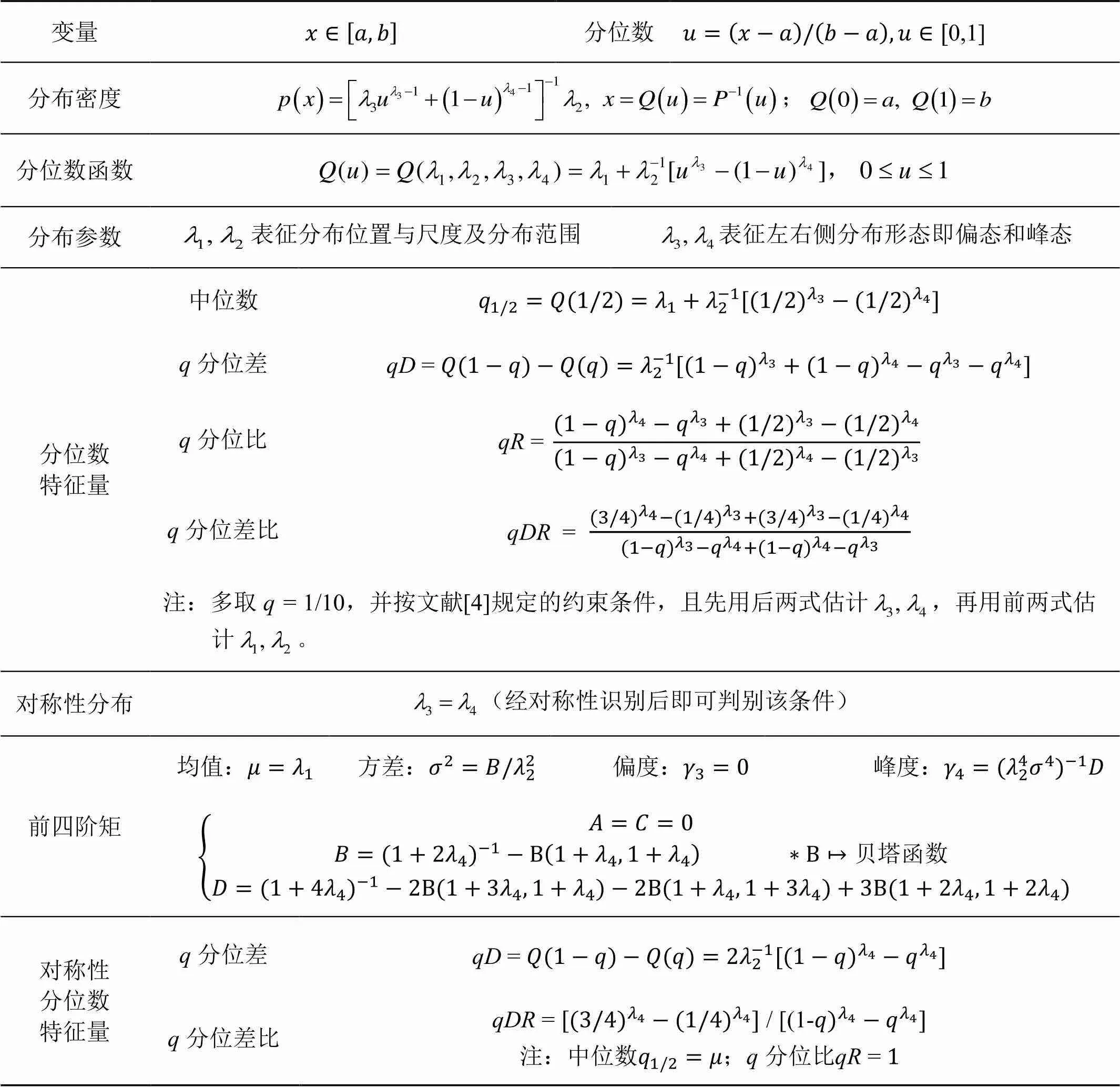
表2 λ分布统示法

同理，关于分布实际运用见文献[4,8]，这里仅概述其特点及实用中的问题：

1）分布更便于以分位数表述，只是拟合概率分布中应顾及分布参数所适应值域，然而其适应的条件较复杂，难以校验分布参数的适应阈值；

2）分布形态具有多态性，所能覆盖的实际分布较分布的覆盖面更广，尤其可涵盖拖尾分布，适于应用到寿命、磨损等专业范围，却仍未能覆盖多峰型分布；

3）现代智能算法尤其具有全局优化性能者可用于拟合分布（无论利用分位数法还是样本矩法），只是运用分位数法拟合分布中，其样本容量不宜过小，可借MC方法利用自助（Bootstrap）样本予以增大；

4）为简化拟合分布，尽量经对称性识别，按对称性优先的处理原则；

2.1.2 展开式分布族

据函数逼近论，满足一定条件的正交多项式可对任一连续函数作最佳逼近，文献[2]已证得Hermite正交多项式可逼近概率分布函数，构成其在实用中的展开式：Gram-Charlier级数、Edgeworth级数等的理论依据。

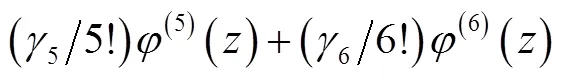
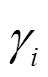
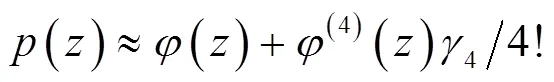
显然，实质上是直接依据统计特征量表示分布函数的方法。

利用一种通用办法，借MC方法求数值积分，即

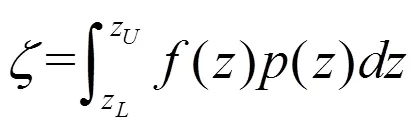
由于运用高价标准化累积量，就可方便地表示分布函数，然而需计算标准化正态分布密度及其阶导数或查找其数值表；通用MC方法，可得待求分布统计特性数值，但运算量大。当前随机性分布统示方法及其拟合处理手段已大有发展提高，故已较少运用展开式统示法。

2.1.3 混合分布类型

为适于更复杂分布，特别是多峰型分布，上世纪末出现应用混合分布类型，尤其是高斯混合模型（Gaussian mixture model, GMM），即2～5个高斯分布线性组合：

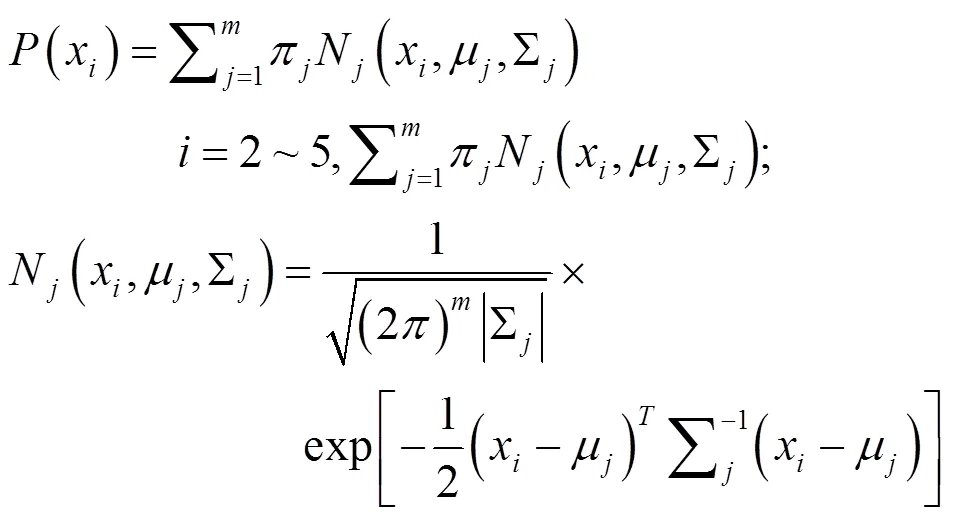
GMM优异之处在于其分布覆盖面最大，含对称、非对称、拖尾型，特别是涵盖多峰型，已成为应用渐广的分布统示法。但预先难定混合模型，需拟合分布处理后才能定型。故采用含隐变量参数的分布拟合处理方法，如EM算法。虽算法复杂，有时迭代算法收敛较慢，计算时间较长，却可用现成软件，但对于含隐参数的数据处理方法值得改进完善。

EM算法由Dempster等于1977年提出，用于含隐变量下求后验分布众数的极大似然估计迭代算法。交替利用求期望和最大化两步迭代计算求得最大对数似然期望估计。

E-step（求期望）：用当前参数评估响应后验概率

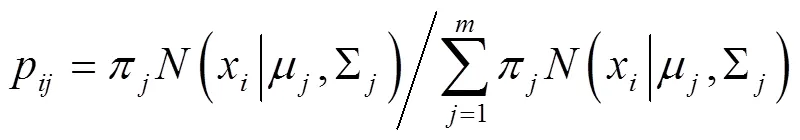
M-step（最大化）：用当前参数值重新评估参数

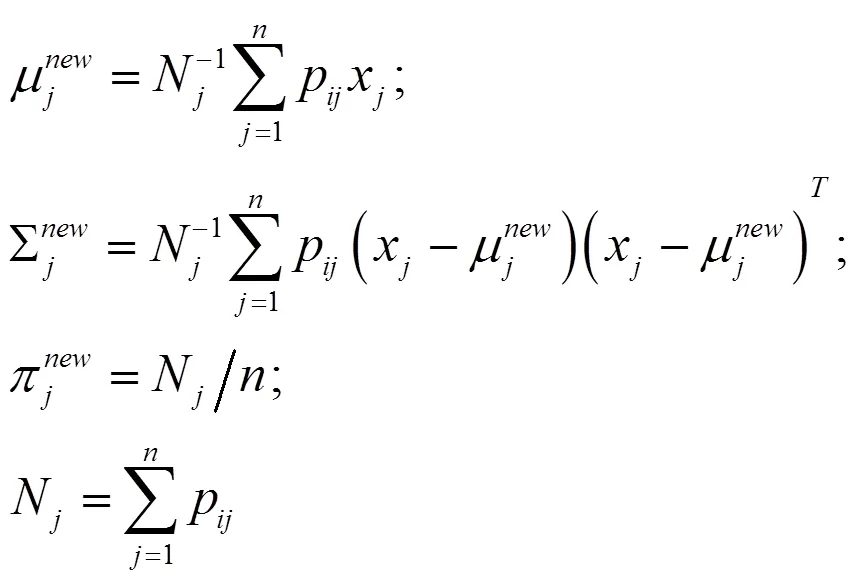
两步迭代计算至收敛。最终，评估对数似然：

2.2 基于频率分布的近似方法

统计试验所得到的频率分布如直方图、折线图等，在样本容量足够大时，能较全面地显现出随机现象的总体统计特性[2,9]。然而，实用中样本容量并不大或在小样本下，可用折线分布逼近直方图的方法使其体现总体统计特性更具代表性。前苏联于上世纪中叶采用四段对称折线分布逼近法，未能覆盖非对称分布类。作者也用过两段折线分布逼近法，用以统示常见的对称、非对称分布[10]。看之似粗略，实则经拟合优度检验表明与其他方法效果相近，且简便、实用。

多参数折线分布密度、分布图及不同参数下可表示的分布图形分类表分别如式(8)、图1、表3所示。

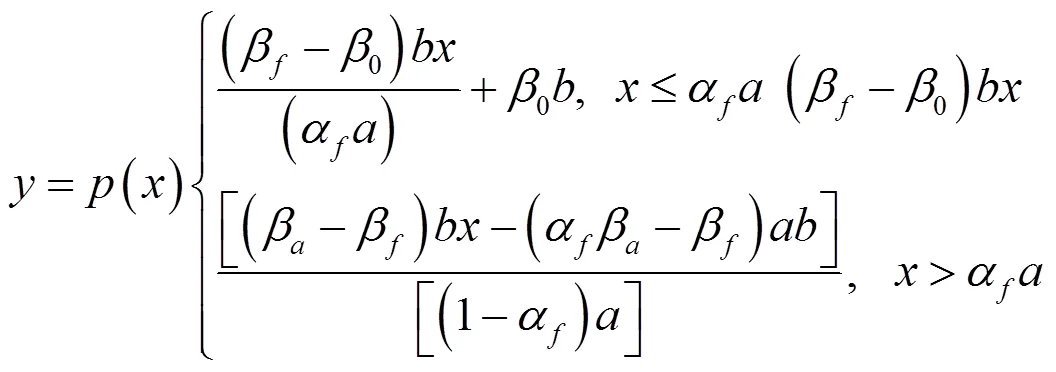
图1 多参数折线分布图

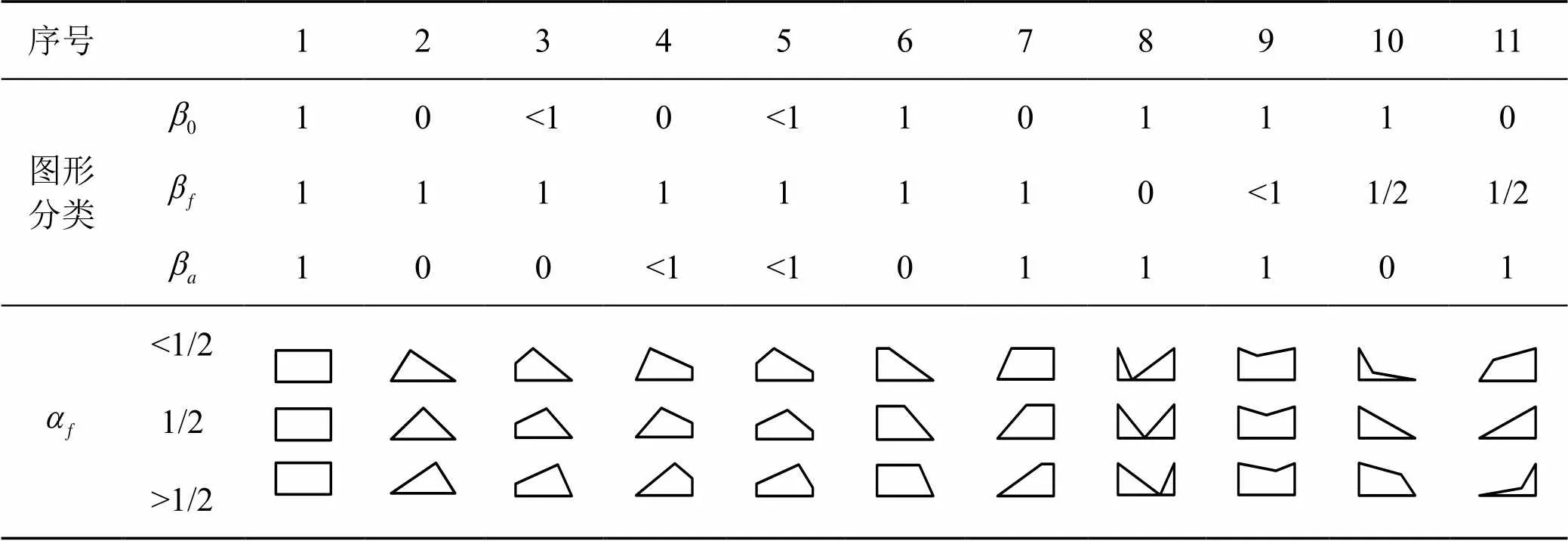
表3 不同参数下可表示的分布图形分类表

注：3与4；6与7；10与11互为对称。

应用结果表明：由于基于统计试验所得的频率分布更贴合现实，仅运用直线构成分布函数，又有一定的覆盖面，简便、易用，故多参数折线分布统示法对于小样本统计分析具有实用价值。然而，毕竟仅能粗略体现总体统计特性，不含拖尾型、多峰型分布，其覆盖面有限。若改进为6参数三段折线分布，将逼近更佳，覆盖面更大，可扩展其应用范围。然而，同样因分布统示方法及其拟合处理手段已发展提高，故少用。

2.3 基于样本数据的直接方法

无论何种分布统示法无不基于样本数据，若能仿真所需随机性分布的样本数据列（数据量足够大)，也就可直接得出其总体统计特性，此即构成样本数据直接统示法的思想。马尔科夫链蒙特卡罗（Markov Chain Monte Carlo, MCMC）方法可用于实现该思路，尤其适于解决复杂分布、高维分布等难题，因而近年来得到广泛应用。如文献[11,12-实例3]的粒子滤波就用到MCMC方法。

MCMC方法始于上世纪中叶，在MCMC中后一MC即熟知的生成随机序列的蒙特卡罗方法，主要利用前一MC即马尔科夫链。它具有无记忆/无后效性也直接称为马尔科夫性：设随机过程{(),∈}，对于内任意1个时间参数1<2<...<t<t+1和取值状态空间内任意1个状态1,2,...,j,j+1，若下述条件概率关系恒成立：

{(t+1) =j+1|(1) =1,(2)=2,...,(t) =j}

={(t+1)=j+1|(t) =j} (9)

则称此过程为马尔科夫链。满足式(9)的性质称为马尔科夫性。可理解为：已知系统现在状况下，系统将来变化状况只取决于现在状况，而与系统过去经历状况无关。马尔科夫链状态空间是离散的，而参数集可为离散（未必是等间隔的）或连续的两类。

注意，并非所有马尔可夫链都可用于统示法。只有一定条件下，如齐次性、遍历性（不可约性、非周期性）等经过足够多步转移后，能收敛至平稳性序列的齐次马尔可夫链才能用于统示法。核心问题在于一步转移概率；离散马尔科夫链()在时刻t由状态一步转移到状态的一步转移概率，简称转移概率，也称转移核为

{(t+1) =|(t) =} =p(t) (10)

马尔科夫链转移概率不依赖于时间参数，具有齐次性，即p(t) =p。

MCMC方法核心在于运用某些专有方法所需平稳分布构造转移核（如Gibbs算法、Metropolis-Hasting (M-H)算法等），使之得出样本序列（如后验分布样本数据）。MCMC方法因其通用性，适用于复杂分布与高维问题，且已有些可选软件而得到广泛应用，尤其可解决不少难题。但有时转移次数偏多，计算量较大，迭代收敛较慢[13]。

3 结语

1）基本观念：随机性分布模式以非高斯性为常态，导致研究并应用分布统示法。

2）目标：最本质或够准确的总体规律，目的在于获得研究课题待求的总体统计特性。

3）依据：样本信息、先验信息。在以非高斯性为常态下，应获取样本高价矩/分位数和可靠而重要的先验信息，并导致研究运用先验信息的方法（如贝叶斯统计推论等具体方法）。

4）推论原则：特殊到特殊的转导推理，具体化为依据所得到的样本高价矩/分位数并辅以可靠先验信息而估计出统示分布参数，直接统计推论待求的总体统计特性（无需追究其理论概率分布）。

5）处理方法：对称性优先，以及实用性、普适性全局优化智能算法。导致研究分布对称性简易识别

上述虽针对统示法，其核心思路具有普适性，尤其前面5条应是一般误差分析及数据处理之通则。

[1] 林洪桦.测量误差分析及数据处理若干要点系列论文（一）——现代数据处理基本观念与四字要诀[J].自动化与信息工程,2020,41(1):1-4,9.

[2] 林洪桦.测量误差与不确定度评估[M].北京:机械工业出版社,2010.

[3] Hart H, Hartig C. Non-Gaussion error boundaries, In: Measurement for progress in science and technology, North Holland, 1980.

[4] Karian Z A, Dudewicz E J. Fitting Statistical Distributions: The Generalized Distribution and Generalized Bootstrap Methods CRC Press, 2000.

[5] 林洪桦.再荐误差的分布统示法[J].中国计量学院学报，2004(2):96-101.

[6] 林洪桦,潘峰.重复测量数据分布的自助法估计[J].北京理工大学学报,2004(11):947-951.

[7] 席同鑫,林洪桦,王中宇.误差分布对称性的识别方法研究 [J].电子测量与仪器学报, 2010(增刊):39-44.

[8] 林洪桦,席同鑫,王中宇.分布统示法用于小样本数据处理的探讨[C].第十一次全国误差理论与不确定度学术与教学交流研讨会,海南三亚,2011.

[9] 林洪桦,马升.误差分布及其合成分布差判别的数值仿真分析[C].全国计量测试学术大会论文集,计量学报期刊社,1998.

[10] 林洪桦,吴春增.折线分布及其在精度分析中的应用[J].北京理工大学学报,1994,14(2):145-152.

[11] Shuhui Li, Xiaoxue Feng, Honghua Lin, et al. Joint state and parameter estimation for stationary ARMA model with unknown noise [C]//第36届中国控制会议论文集（B）,2017-07,中国辽宁大连:s.n.,2017:607-612.

[12] 林洪桦.探讨小样本下“三非”问题的分析与处理[C].第十四次全国误差理论与不确定度学术与教学交流研讨会,南京,2018.

[13] 刘金山,夏强.基于MCMC算法的贝叶斯统计方法[M].北京:科学出版社,2016.

Some Key Points of Measurement Error Analysis and Data Processing Series Papers (2)——An Overview of Random Distribution Uniform Expression Method

Lin Honghua

(Beijing Institute of Technology, Beijing 10081, China)

This paper expounds the necessity and representation of random distribution uniform expression method in modern data processing, including theoretical method based on distribution function, approximate method based on frequency distribution, direct method based on sample data, the characteristics of each and the problems that should be paid attention to in practice are summarized. The key points such as basic concept, objective, basis, inference principle, processing method for error analysis and data processing are summed up, which are combined touniform expression method,and the selection method of uniform expression method is clarified.

data processing; mathematical model; error; uniform expression method

林洪桦，男，1932年生，教授，主要研究方向：测试误差分析及数据处理。

TP274

A

1674-2605(2020)02-0001-07

10.3969/j.issn.1674-2605.2020.02.001