基于EMD样本熵与改进DS证据理论的故障诊断方法*

郑日晖　岑健　陈志豪　熊建斌

基于EMD样本熵与改进DS证据理论的故障诊断方法*

郑日晖1,2,3岑健1,2陈志豪1,2熊建斌1,2

（1.广东技术师范大学，广东 广州 510665 2.广州市智慧建筑设备信息集成与控制重点实验室， 广东 广州 510665 3.广东水利电力职业技术学院，广东 广州 510635）

针对单一传感器故障诊断信息源简单、信息不完整的局限性，提出一种基于经验模态分解样本熵与改进DS证据理论的多传感器信息融合故障诊断方法。该方法对每路传感器采集的振动信号进行经验模态分解，并计算其固有模态函数IMF的样本熵作为故障特征变量；将故障特征变量输入事先训练好的各个随机森林分类器进行分类；以每个随机森林的分类结果作为证据体，采用改进的DS证据理论进行融合并输出最终分类结果，实现多个传感器信息有效融合，各传感器间形成信息互补，达到优化决策目的。实验结果表明：该方法故障诊断准确率达98.85%，且具有鲁棒性。

故障诊断；经验模态分解样本熵；随机森林；DS证据理论；信息融合

0 引言

利用传感器采集机械故障信息是故障诊断的重要环节之一[1]，但由于受到工作环境以及传感器本身性能的约束，单一传感器提供的信息有限、不完整。依靠单一传感器的信息进行故障诊断，准确率难以提高、鲁棒性较差。因此，多传感器信息融合技术被广泛应用于故障诊断领域，而DS（Dempster-Shafer）证据理论在多传感器信息融合故障诊断中发挥了重要作用。王晶晶等[2]采用DS证据理论与不精确概率理论相结合的方法对多传感器信息进行融合，并通过实验证明该方法在振动故障诊断方面的有效性；Cheng等[3]采用DS证据理论对SOM神经网络的输出进行多传感器信息融合；Jiang等[4]采用DS证据理论进行多传感器决策级融合并用于旋转机械故障诊断。尽管DS证据理论在信息融合中取得良好成效，但存在以下缺陷：1）如果冲突因子较大，合成结果不理想，甚至可能导致与直观情况相违背的现象；2）鲁棒性较差；3）存在“一票否决”现象，影响信息融合准确率的进一步提高。

本文将经验模态分解（empirical mode decompos-tion, EMD）样本熵[5]与随机森林分类算法相结合构建诊断单元；对传统DS证据理论的缺陷进行改进，并采用改进的DS证据理论对来源于多个诊断单元的识别信息进行融合，得到最终识别结果。

1　EMD样本熵

EMD样本熵诊断单元结构图如图1所示，包含信号采集、信号分析、特征提取、模式识别、信息输出5部分。诊断单元信号来源于安装在机械设备不同位置的传感器。

图1　EMD样本熵诊断单元结构图

振动信号包含各种随机过程的耦合成分，且具有较强的非平稳性，因此直接对原始振动信号进行特征提取效果不理想[6]。EMD可对信号进行自适应、多分辨分析[7]，将复杂振动信号按照不同的时间尺度分解为若干个固有模态函数（intrinsic mode function, IMF）分量和1个单调余量，可有效平稳振动信号，适用于非平稳信号的分析与处理[8]。

为更全面、合理地提取故障特征，本文采用EMD将来源于多个同质传感器的振动信号分解为若干个IMF分量，进一步计算各个IMF分量的样本熵并将其作为振动信号的特征向量。IMF分量样本熵具体计算方法[9]如下：

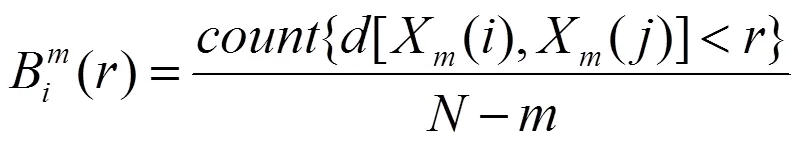
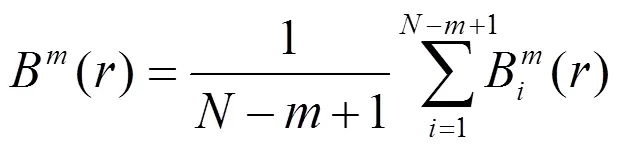
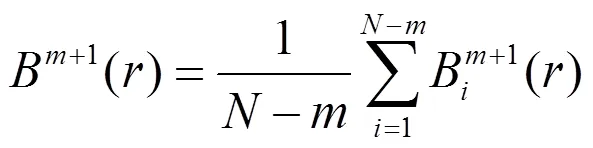
6）理论上定义样本熵

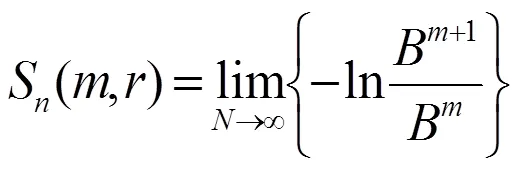
工程实际中，数据点数为有限值，计算过程通常采用

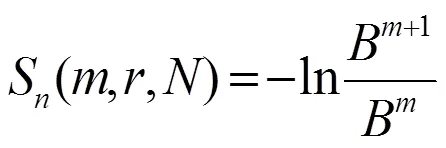
2　DS证据理论及其改进

2.1　传统DS证据理论[11]

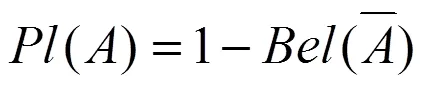
传统DS证据理论提出，当有2个证据体存在时，按以下规则进行组合：

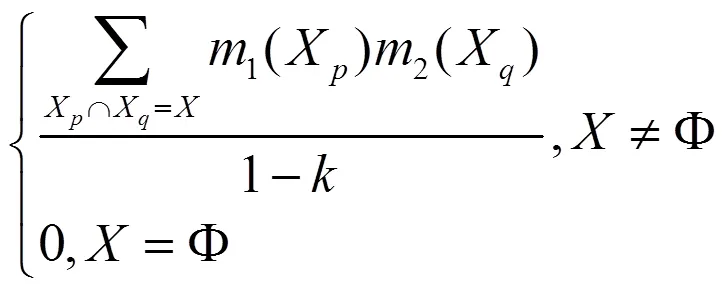
式中为冲突因子，计算公式为

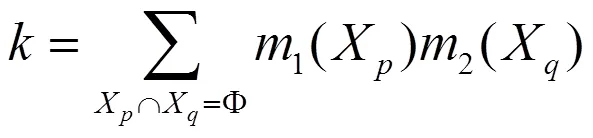
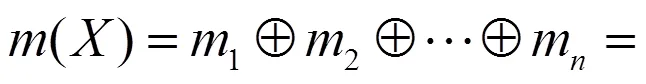
此时冲突因子

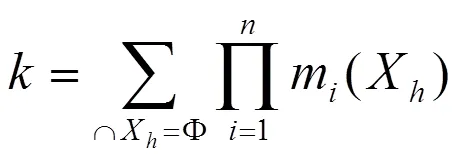
2.2　基于Cosine相似度的改进方法

针对传统DS证据理论存在的缺陷，几十年来国内外专家学者对其改进方法进行了大量研究，主要分为3大类：第一类是修改组合规则；第二类是修改模型；第三类是同时修改模型和组合规则。由于传统DS证据理论的组合规则本身具有坚实的数学基础，故本文选择修改模型而不修改组合规则的方法。考虑到采用距离计算证据相似度的方法需要寻求两者间映射关系，且映射关系的选择直接影响权重系数的合理性和可靠性，故本文采用Cosine相似度直接计算证据体间的相互支持度。将Cosine相似度累加并归一化得到证据体的可信度；以可信度作为权重系数对证据体进行加权平均；以加权平均证据体替代原始证据体；最终采用DS证据组合规则进行合成。采用加权平均的方法对证据体进行处理，不仅有效克服传统DS证据理论存在的缺陷，还充分利用可信度对证据体的权重进行分配，使改进后的模型更合理、改进效果更理想。

1）求各证据之间的Cosine相似度

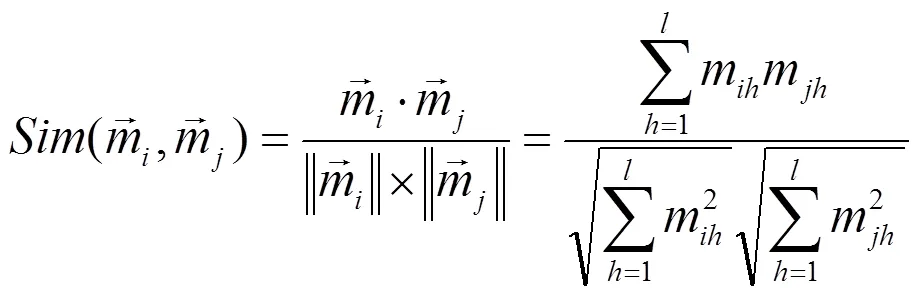
遍历计算任意2个证据体之间的相似度，形成相似性矩阵：

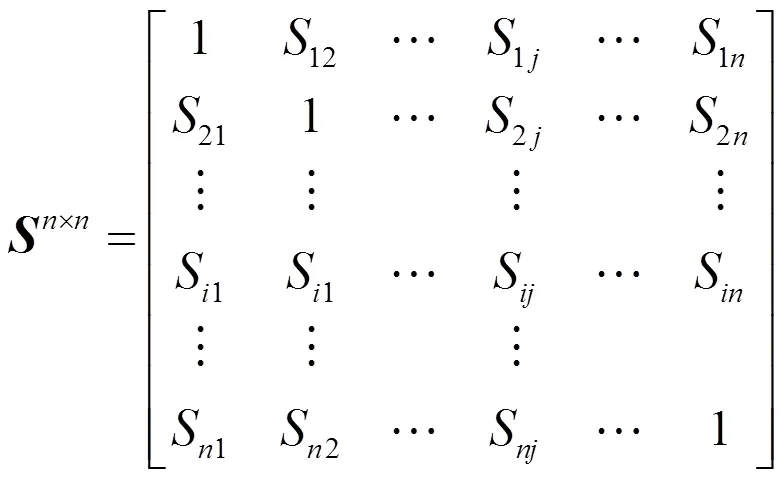
2）求各证据之间的相互支持度

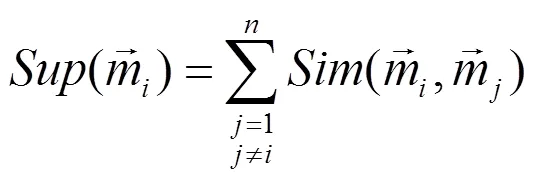
3）求各证据体的权重系数

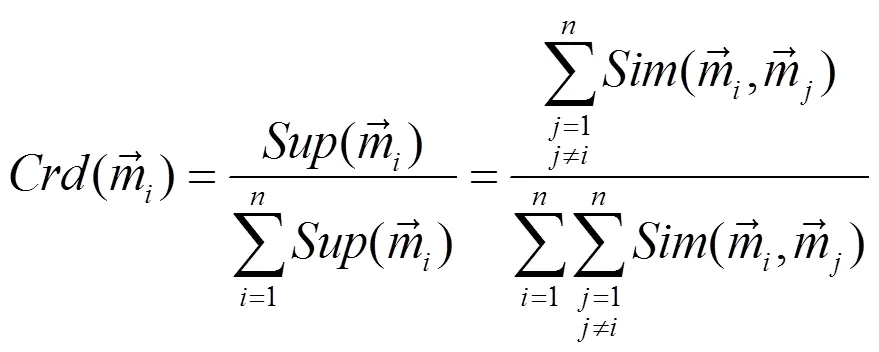
4）求加权平均证据

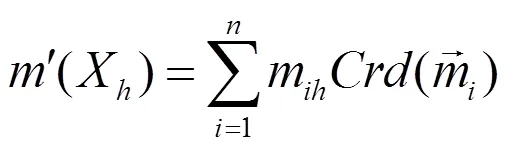
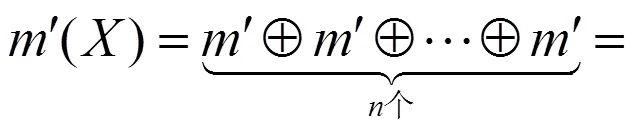
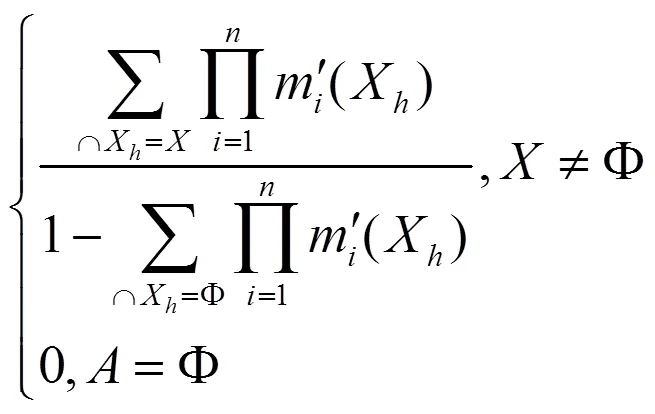
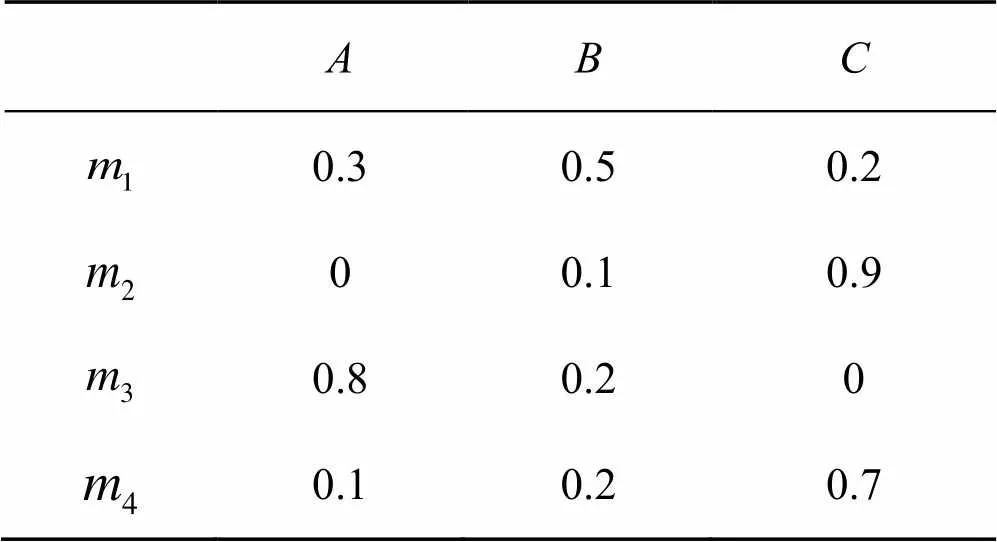
表1　算例1基本概率分配

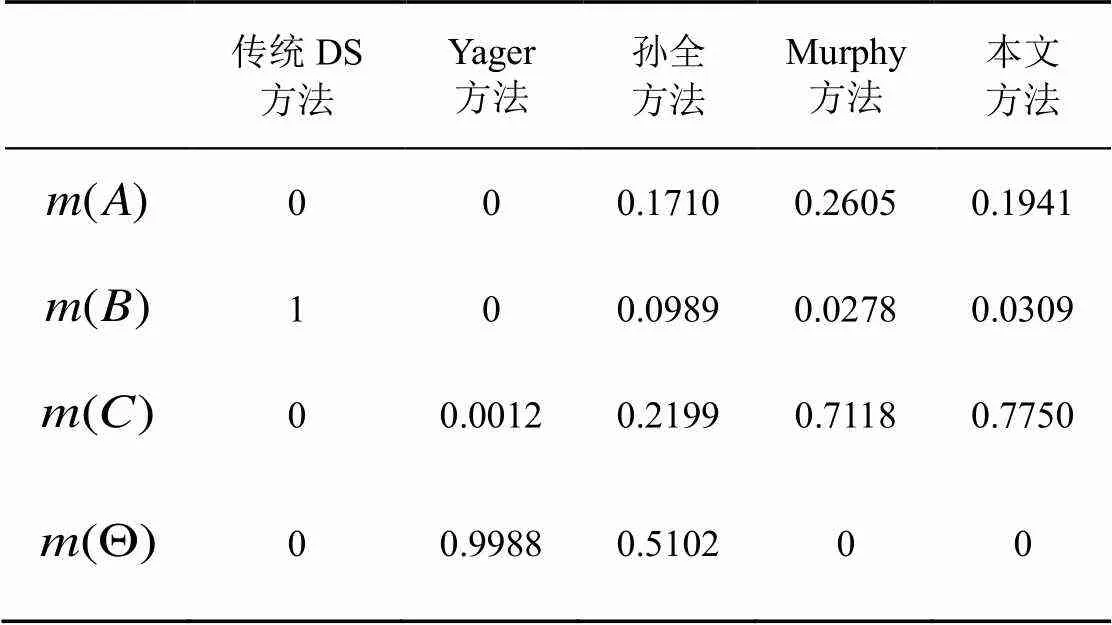
表2　本文方法与其他方法比较

由表2可以看出：由于证据体之间存在较大冲突，传统DS方法完全失效；Yager方法几乎没有任何判断价值；孙全方法虽然可以做出判断，但倾向性明显不足；Murphy方法和本文方法都能得到满意的结果，但本文方法倾向性更明显，融合效果优于其他方法。

3　算法分析

3.1　EMD样本熵特征提取可行性分析

为验证EMD样本熵特征提取方法的可行性，采用美国凯斯西储大学轴承数据中心的部分轴承数据进行仿真[12]。选取其中4种故障类型，每种故障类型共100个样本，样本总数为400个。如果直接对原始故障信号进行样本熵提取，在平面坐标中，400个样本的特征值分布情况如图2所示。如果对故障信号进行EMD，再提取前3层IMF分量的样本熵为特征向量，三维坐标根据3个特征参数标注样本的空间位置，400个样本的空间分布情况如图3所示。

由图2可以看出：直接计算原始信号的样本熵，除故障2外，另外3种故障类型的样本熵数值分布有部分混叠（故障1与故障4、故障3与故障4），甚至完全混叠（故障1与故障3），这样的特征值无法用于识别区分不同类型的故障。

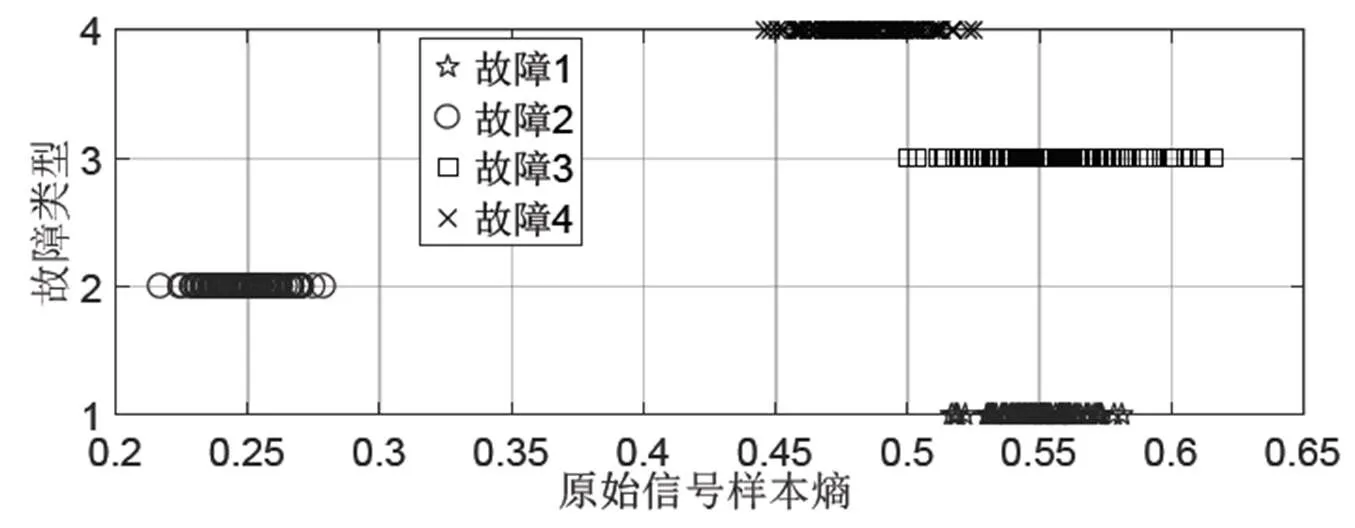
图2　原始信号样本熵分布情况

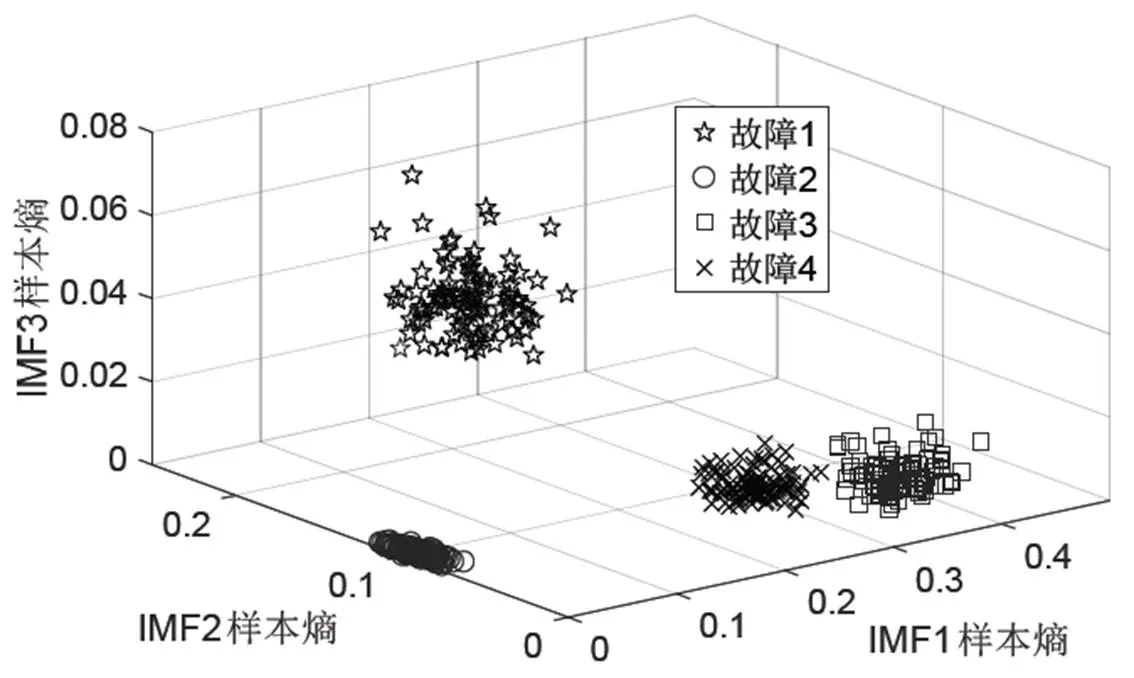
图3　EMD样本熵分布情况

由图3可以看出：通过前3层EMD样本熵，可在样本空间中将4种故障清晰地区分开，这说明前3层EMD样本熵适合作为识别故障的特征向量。

3.2　随机森林与DS证据理论结合的可行性分析

为实现诊断单元的智能化，诊断单元采用机器学习算法中的随机森林分类器根据特征向量对故障进行识别诊断。随机森林分类器是采用决策树进行组合的集成算法，不仅准确率高、运算速度快，并且能有效容忍噪声，具有较强的鲁棒性[13]。运用DS证据理论进行决策融合的前提是BPA的有效获取[14]，而随机森林分类算法采用决策树投票的方式获得输出，投票结果反映了对判别结果的支持程度，因此将随机森林分类器的投票结果作为证据，求出每种故障类型的得票数占决策树总数的比例即可作为DS证据理论的BPA，这也是将随机森林算法与DS证据理论进行结合的巧妙之处。

4　实例验证

4.1　故障诊断流程

随机森林是机器学习算法，需采用历史数据进行训练才能用于模式识别[15]。因此，本文故障诊断方法分为线下训练和在线诊断2部分。

线下训练每一个诊断单元独立进行，诊断单元的随机森林分类器训练流程如图4所示，具体步骤如下：

1）采集该位置的各类故障信号作为训练样本；

2）对训练样本进行EMD；

3）选取训练样本前3层IMF分量并计算每个IMF分量的样本熵；

4）以前3层IMF分量的样本熵作为输入变量对随机森林分类器进行训练。

图4　诊断单元的随机森林分类器训练流程

基于EMD样本熵与改进DS证据理论的多传感器信息融合故障诊断流程如图5所示，具体步骤如下：

1）各位置传感器分别对该位置的振动信号（实际中同一时刻为同类故障）进行采集；

2）各诊断单元对传感器采集的振动信号进行EMD，计算前3层IMF分量的样本熵构成特征向量，将特征向量输入训练好的随机森林分类器并获得各类故障的投票结果；

3）将每个诊断单元的输出信息转化为BPA，为决策融合提供证据体；

4）采用改进的DS证据组合理论对每个诊断单元的证据进行决策融合并输出诊断结果。

图5　多传感器信息融合的故障诊断流程

4.2　实验结果分析

为验证本文提出的多传感器信息融合故障诊断方法，选用美国凯斯西储大学轴承数据中采样频率为12 kHz、故障直径为0.1778 mm、电机载荷为735 W条件下驱动端轴承的4种故障数据：内圈故障（故障1）、滚动体故障（故障2）、外圈故障6点钟方位（故障3）、外圈故障3点钟方位（故障4）。以上4种故障数据中，每种故障数据均含有基座、风扇端底座、驱动端底座3个位置的振动信号数据。因此，实例采用3个诊断单元进行信息融合。

从传感器通信的角度来看，基座、风扇端底座和驱动端底座3个位置的传感器都能采集到以上4种故障的振动信号。每个位置对应每个诊断单元，每个诊断单元的每种故障都选取100个样本供训练和测试，这样每个诊断单元都有400个样本。将每个诊断单元的400个样本随机抽取300个作为相应随机森林分类器的训练样本（3个诊断单元共3组），其余100个作为测试样本（3个诊断单元共3组）。需要说明的是：实际过程中，同一时刻每个位置的传感器采集到的是同一种故障类型的信号。本文实验为保证测试时每次输入3个诊断单元的信号来自于同类故障，在随机抽取训练数据和测试数据时，3个诊断单元的样本抽取均采用同样的随机序列。

按图5所示故障诊断流程，每个诊断单元按相同的随机序列随机抽取300个数据样本对相应的随机森林分类器进行训练，其余的数据样本（共3组，每组100个，按相同的随机排序）用于测试。采用3组测试样本模拟在线诊断，每次同时在3个诊断单元输入相同故障类型但来源于不同位置的故障样本进行测试。3个诊断单元对3组测试样本中4类故障进行识别分类的单次实验（每个诊断单元都用完100个测试样本）结果分别如图6、图7、图8所示。可以看出：3个诊断单元的诊断准确率分别为80%，91%，87%。

图6　第1个诊断单元分类结果

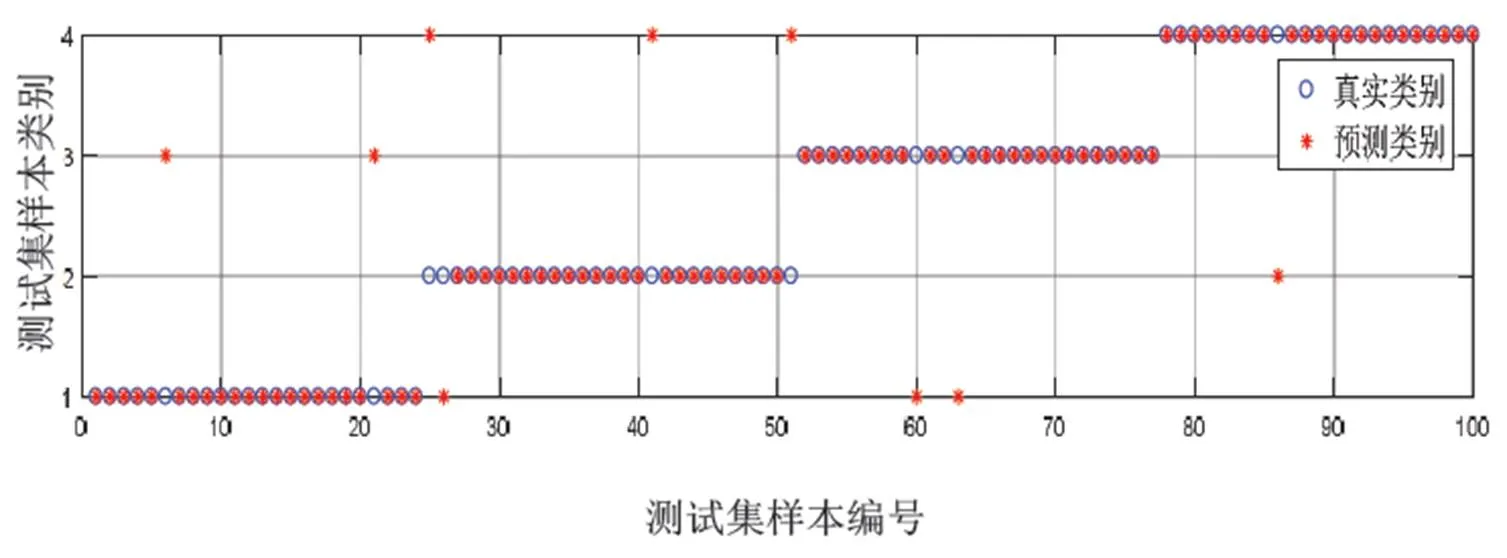
图7　第2个诊断单元分类结果

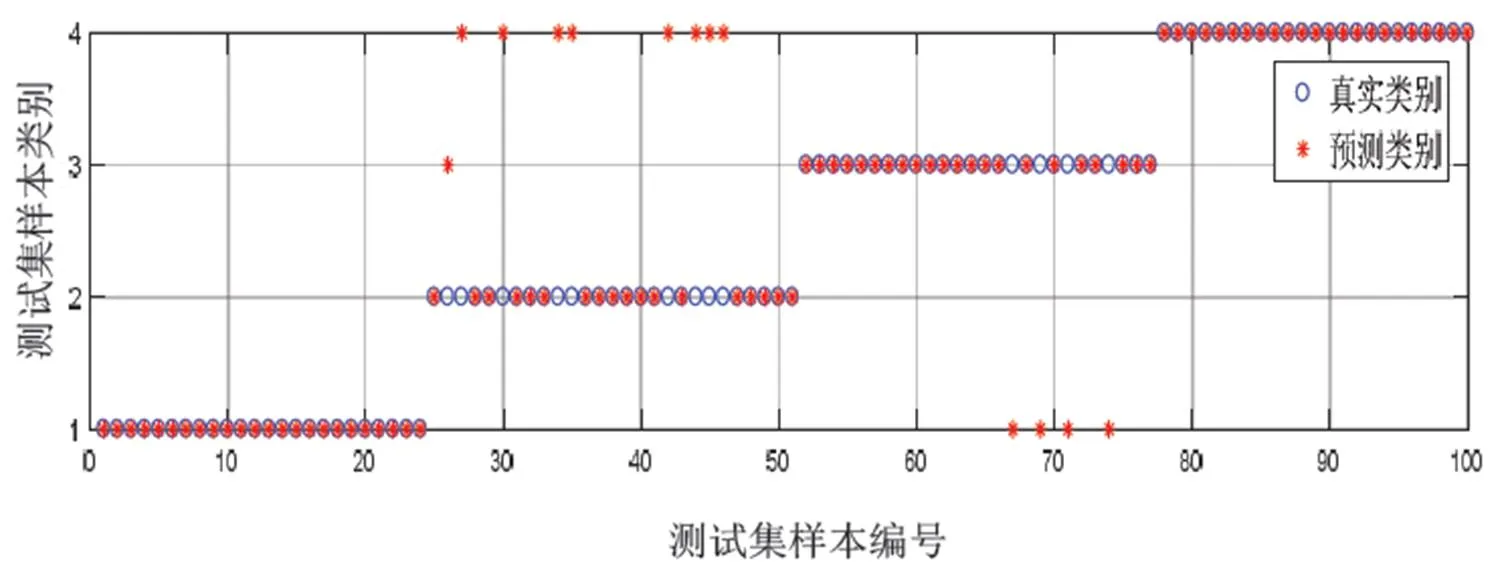
图8　第3个诊断单元分类结果

根据每个随机森林中决策树的投票情况，求出每个样本测试结果中每种故障类型得票数占决策树总数（本文为500）的比例，并以该比例作为BPA。每个样本测试均采用传统DS证据理论对3个诊断单元的输出信息进行融合，形成1个诊断结果，每个诊断单元都进行100个样本的测试，融合后的100个诊断结果如图9所示。由图9可以看出：采用传统DS证据理论融合后的诊断准确率为96%。

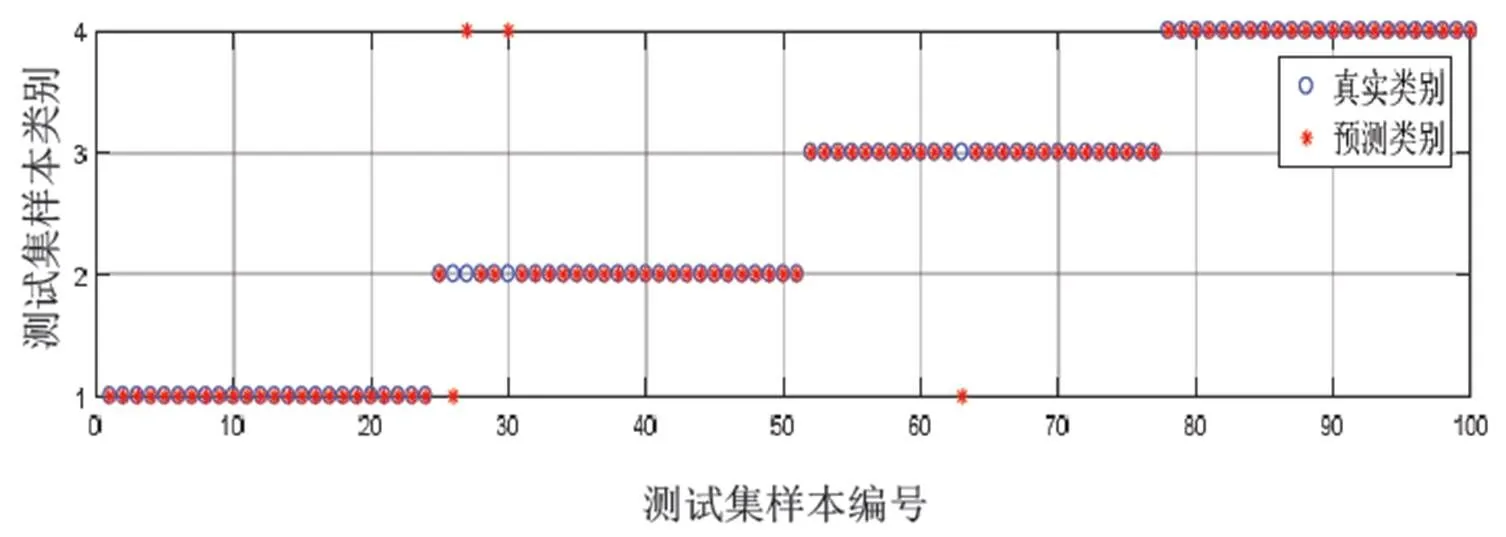
图9　传统DS证据理论融合分类结果

同样以每种故障类型得票数占决策树总数的比例为BPA，采用改进的DS证据理论进行融合，融合后的100个诊断结果如图10所示。对比图9与图10可知：改进前有4个样本分类错误，改进后纠正了其中2个样本，使诊断准确率进一步提高到98%。

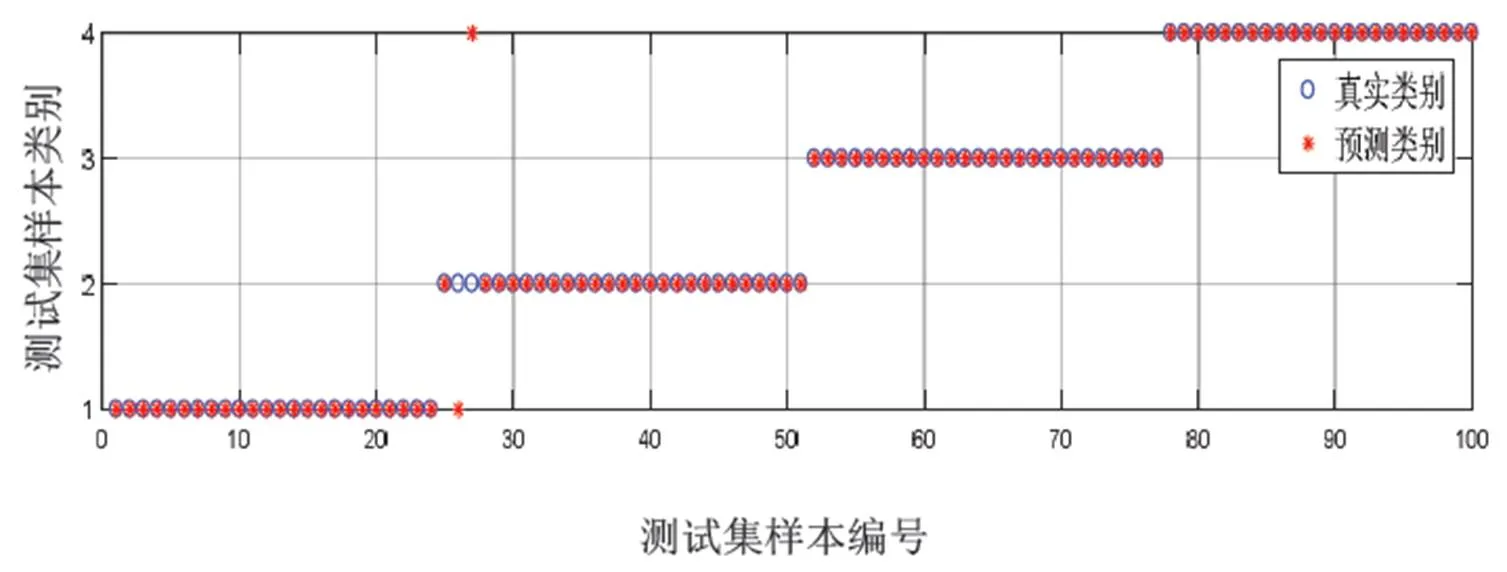
图10　改进DS证据理论融合分类结果

由以上单次实验的结果可以看出；基于DS证据理论的多传感器信息融合明显地提高了故障诊断准确率，且改进DS证据理论后诊断准确率进一步提升。同时，对比图6~图10发现：第1个诊断单元对故障3的诊断准确率很低，但通过信息融合后另外2个诊断单元对其进行了信息补充，使故障3的诊断准确率大幅度提升，这说明多传感器信息融合可以相互补充、有效克服单一传感器信息不完整问题。

为消除随机误差、更充分地验证本文方法的有效性，随机独立重复实验20次。3个诊断单元、传统DS证据理论融合、改进的DS证据理论融合每次实验的诊断准确率如图11所示。以上5种情况20次实验的平均诊断准确率、标准差统计结果如表3所示。

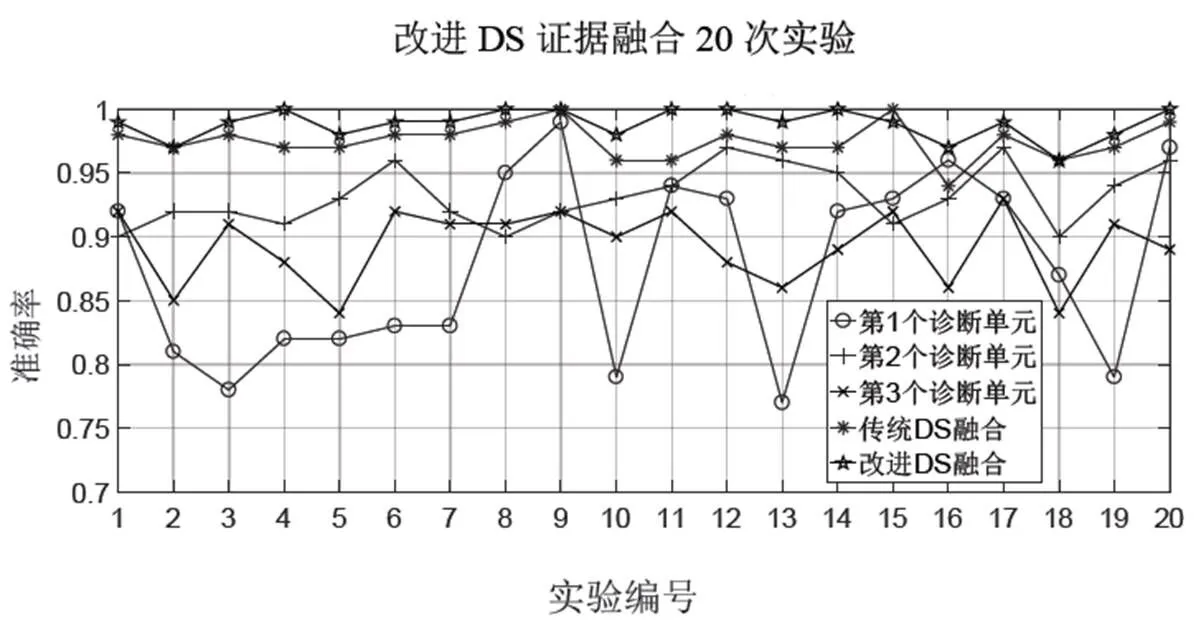
图11　随机独立重复实验20次分类结果

表3　随机独立重复实验20次统计结果

由图11及表3可以看出：1）单靠1个诊断单元进行故障诊断时诊断准确率都不高，分别为87.75%，93.20%，89.30%，采用传统DS证据理论将3个诊断单元的信息进行融合后诊断准确率明显提高，为97.50%，而经过改进的DS证据理论融合，诊断准确率进一步提高到98.85%；2）尽管第1个诊断单元的诊断准确率随机变动很大，标准差达7.30%，但由于经过融合后3个诊断单元之间形成有效互补作用，传统DS融合方法和改进的DS融合方法的诊断准确率都相对比较稳定，标准差仅为1.43%和1.18%。

5　结论

本文采用基于Cosine相似度改进的DS证据理论对来源于多个诊断单元的识别信息进行融合。诊断单元将来源于不同传感器的振动信号进行EMD后计算其IMF分量的样本熵，以EMD样本熵为特征变量输入随机森林分类器进行分类并输出投票结果。将诊断单元的投票结果转换为BPA，采用改进后的DS证据理论进行融合得到最终的诊断结果。经实验验证：本文提出的多传感器信息融合故障诊断方法不仅可以克服单一传感器信息不完整问题，还可以有效提高故障诊断准确率，并且比单一传感器故障诊断更具有鲁棒性。

[1] 苏乃权,熊建斌,张清华,等.旋转机械故障诊断研究方法综述[J].机床与液压,2018,46(7):133-139.

[2] 王晶晶,梁青.基于证据理论与不精确概率的振动故障诊断[J].传感器与微系统,2018,37(6):108-111.

[3] Cheng G, Chen X H, Shan X L, et a1. A new method of gear fault diagnosis in strong noise based on multi-sensor information fusion[J]. Journa1 of Vibration and Contro1, 2016, 22(6):1504-1515.

[4] Jiang W, Wei B Y, Xie C H, et a1. An evidentia1 sensor fusion method in fault diagnosis[J]. Advances in Mechanical Engineering, 2016, 8 (3):1-7.

[5] 魏文军,刘新发.基于EEMD多尺度样本熵的S700K转辙机故障诊断[J].中南大学学报(自然科学版),2019,50(11):2763-2772.

[6] 陈强强,戴邵武,戴洪德,等.基于IMF特征提取的滚动轴承故障诊断[J].噪声与振动控制,2020,40(1):46-50.

[7] 张安安,黄晋英,卫洁洁,等.基于EMD-SVD与PNN的行星齿轮箱故障诊断研究[J].机械传动,2018,42(12):160-165.

[8] 王海龙,夏筱筠,孙维堂.基于EMD与卷积神经网络的滚动轴承故障诊断[J].组合机床与自动化加工技术,2019(10):46-48,52.

[9] Alcaraz R, Rieta J J. A review on sample entropy applications for the non-invasive analysis of atria1 fibril1ation electrocardiograms[J]. Biomedical Signal Processing and Control, 2010, 5(1): 1-14.

[10] Pincus S M. Assessing serial irregularity and its implications for health[J]. Annals of the New York Academy of Sciences, 2001, 954 (1) :245-267.

[11] Shafer G．A mathematical theory of evidence[M].Princeton: Princeton University Press,1976．

[12] 赵光权,姜泽东,胡聪,等.基于小波包能量熵和DBN的轴承故障诊断[J].电子测量与仪器学报,2019,33(2):32-38.

[13] 张钰,陈珺,王晓峰,等.随机森林在滚动轴承故障诊断中的应用[J].计算机工程与应用,2018,54(6):100-104,114.

[14] 宝石,许军.基于证据理论与多模型结合的模拟电路故障诊断[J].火力与指挥控制,2018,43(7):145-150.

[15] 李兵,韩睿,何怡刚,等.改进随机森林算法在电机轴承故障诊断中的应用[J].中国电机工程学报,2020,40(4):1310-1319, 1422.

Fault Diagnosis Method Based on EMD Sample Entropy and Improved DS Evidence Theory

Zheng Rihui1,2,3Cen Jian1,2Chen Zhihao1,2Xiong Jianbin1,2

(1. Guangdong Polytechnic Normal University, Guangzhou 510665, China 2. Guangzhou Intelligent Building Equipment Information Integration and Control Key Laboratory, Guangzhou 510665, China 3. Guangdong Polytechnic of Water Resources and Electric Engineering, Guangzhou 510635, China)

Aiming at the limitation of single information source and incomplete information for single sensor fault diagnosis, this paper proposed a fault diagnosis method of multi-sensor information fusion based on empirical mode decomposition (EMD) sample entropy and improved DS evidence theory. In this method, EMD is performed on the vibration signal collected by each sensor, and the sample entropy of its intrinsic mode function (IMF) is calculated as the fault characteristic variable. The fault characteristic variables are input into the previously trained random forest classifiers, and the classification results of each random forest are used as evidence bodies. Then the improved DS evidence theory is used to fuse and output the final classification results. The proposed method realizes the effective information fusion of multiple sensors, and the information between the various sensors is complementary, which achieves the purpose of optimization decision. Results of the experiment show that the accuracy of the method is 98.85%, and it is robust.

fault diagnosis; empirical mode decomposition sample entropy; random forest; DS evidence theory; information fusion

广东省自然科学面上项目（2019A1515010700）；广东省普通高校人工智能重点领域专项项目（2019KZDZX1004）；广东省普通高校重点（自然）项目（2019KZDXM020）；广州市科技计划项目（201903010059）。

郑日晖，男，1986年生，硕士生，主要研究方向：智能故障诊断。E-mail: 617943811@qq.com

岑健（通信作者），女，1967年生，博士，教授，硕士生导师，主要研究方向：智能故障诊断。E-mail: mmcjian@163.com

TP206

A

1674-2605(2020)02-0004-08

10.3969/j.issn.1674-2605.2020.02.004