FeW 的差分故障攻击

谢敏，李嘉琪，田峰

（西安电子科技大学综合业务网理论及关键技术国家重点实验室，陕西 西安 710071）

1 引言

近年来，随着物联网的快速发展，轻量级分组密码算法相关的研究十分热门。传统密码分析方法在轻量级算法研究中取得了不错的成果，如在MIBS[1]、LBlock[2]、TWINE[3]等算法的分析中，利用多种分析方法相结合的方式获得更高轮数的攻击[4-6]。与传统密码分析方法不同，差分故障攻击（DFA,differential fault attack）[7]利用加密算法的特点和最大似然估计技术来推测加密系统中的关键信息，其密钥搜索空间远小于差分密码分析和线性密码分析等方法。故障攻击[8]自提出后一直不断发展和改进，差分故障攻击作为故障攻击的一种方法，对轻量级密码算法构成严重威胁[9-11]。

FeW 是Kumar 等[12]在2014 年提出并于2019 年正式发表的一种轻量级分组密码算法，它可以在规格很小的硬件和微型控制器上实现。此外，Kumar等[13]还提出了一种基于FeW 的哈希函数HeW，它在软硬件实现上都拥有很高的效率。FeW 的设计采用了广义Feistel 结构，分组长度为64 bit，轮数为32 轮，密钥长度分为80 bit 和128 bit 这2 个版本，分别记为FeW-64-80 和FeW-64-128。算法结构中包含半字节置换、非线性层和线性层。FeW 对于差分、不可能差分、线性、零相关、相关密钥等分析方法都具有良好的安全性。Shibayama 等[14]利用高阶差分攻击了12 轮FeW-64-80，时间复杂度和数据复杂度均为263.2。Aayush 等[15]使用神经网络模式识别的技术分析了FeW 算法，实验结果表明，FeW 算法的遗传偏差很小，能有效抵御该类攻击。但是目前还没有人评估过FeW 面对差分故障攻击时的安全性，因此对FeW 进行差分故障攻击是十分必要的。

2 FeW 算法介绍

2.1 FeW 的加密算法

FeW 算法的分组长度为64 bit，密钥长度分为80 bit 和128 bit 这2 种，明文经过32 轮迭代得到密文。该算法采用了广义Feistel 结构，如图1 所示，其中使用到的S 盒如表1 所示。

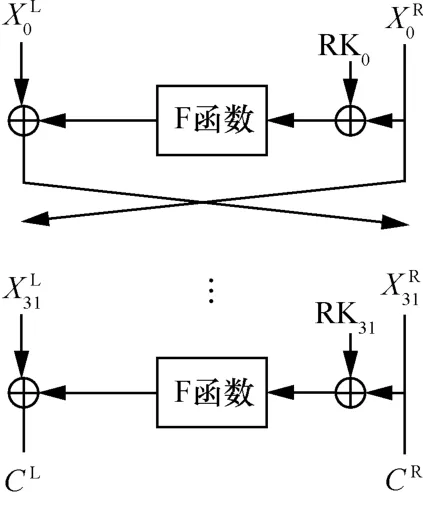
图1 FeW 的轮结构

表1 FeW 的S 盒

2.2 FeW 的F 函数

FeW 的F 函数如图2 所示，它由P 置换（如表2所示）、8 个4 bit 的S 盒以及2 个16 bit 的线性扩散函数L1和L2构成。线性扩散函数L1和L2分别为

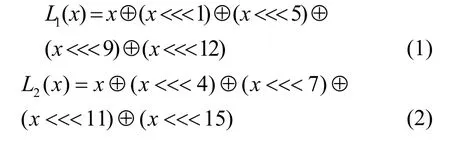
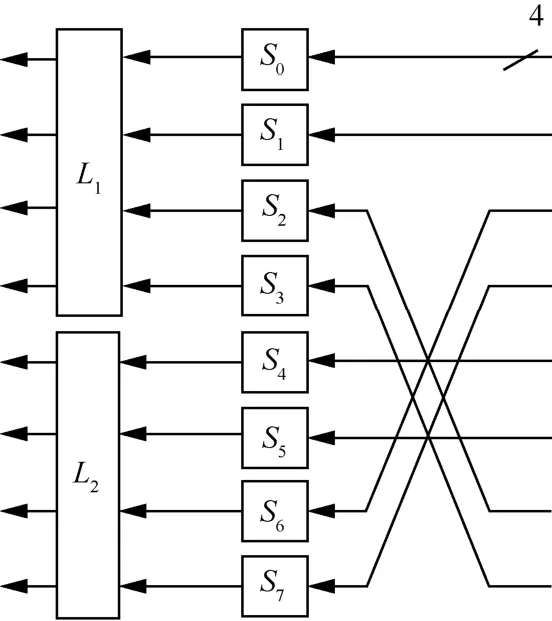
图2 FeW 的F 函数

表2 P 置换

2.3 FeW 的密钥编排算法

2.3.1 FeW-64-80 的密钥编排算法

FeW-64-80 的80 bit 主密钥存储在名为MK=(K0K1…K78K79)的特定寄存器中，并由其更新算法进行64 轮计算，每次取最左侧16 bit 为密钥编排子密钥ki，每2 次更新计算所得共计32 bit 作为轮密钥RKi。当i＜ 64时，MK 的更新算法执行以下计算。

2.3.2 FeW-64-128 的密钥编排算法

FeW-64-128 的 128 bit 主密钥存储在名为MK=(K0K1…K126K127)的特定寄存器中，并由其更新算法进行64 轮计算，每次取最左侧16 bit 为密钥编排子密钥ki，每2 次更新计算所得共计32 bit 作为轮密钥RKi。当i＜ 64时，MK 的更新算法执行以下计算。

3 FeW 的DFA 过程

3.1 故障模型

本文用到的符号说明如下。

i：轮数，0≤i≤31。

Sk：第k个S 盒，0≤k≤7。

IN =(in0,in1,…,in7)：第31 轮中8 个S 盒32 bit输入的半字节块表示。

ΔIN=(Δin0,Δin1,…,Δin7)：第31 轮中8 个S盒32 bit 输入差分的半字节块表示。

OUT=(out0,out1,…,out7)：第31 轮中8 个S盒32 bit 输出的半字节块表示。

ΔOUT=(Δ out0,Δout1,…,Δout7)=(y0y1y2y3…y30y31)：第31 轮中8 个S 盒32 bit 输出差分的半字节块表示和比特表示。

x=(x0x1…x15)：线性扩散函数L1的16 bit 输入的比特表示。

本文采用的故障模型包括以下2 个基本假设。

假设1攻击者可以选择需要的明文，并且可以获得相应的正确密文和错误密文，即选择明文攻击（CPA,chosen plaintext attack）。

假设2攻击者可以在加密过程中的某一轮导入单字节故障，但是故障导入的具体位置和故障值是未知的。

3.2 攻击过程

3.2.1 轮密钥恢复

FeW-64-80 和FeW-64-128 具有相同的轮结构、迭代次数和分组长度，因此以下分析过程对它们均完全适用。

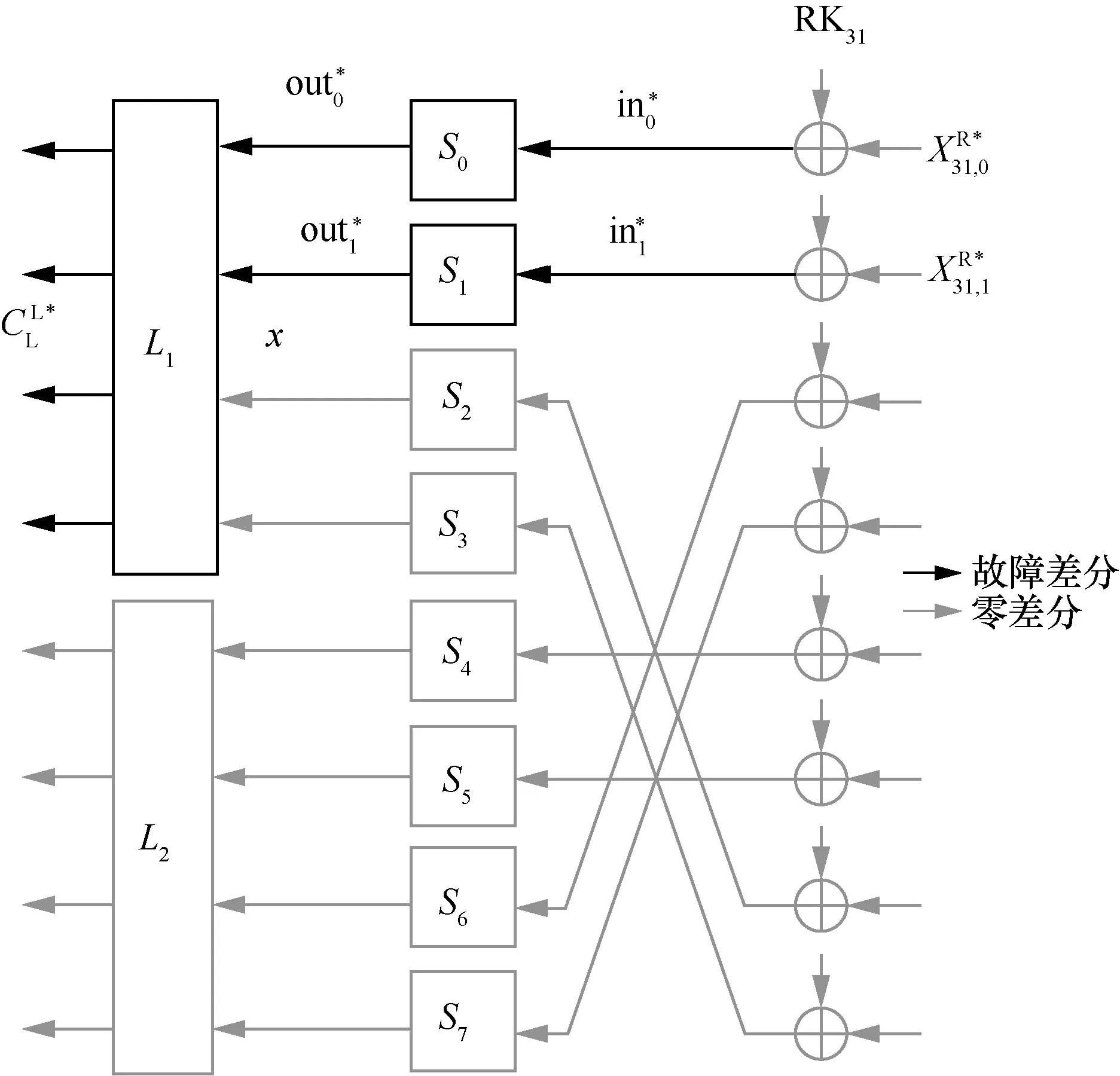
图3 故障传播路径

由图3 可知，该单字节故障经过线性扩散函数L1后会扩散到两字节的密文，即影响密文CL*中最左侧16 bit 的。对于第31 轮右半段的输入和S 盒的输入IN，有，根据FeW 算法最后一轮的结构易知，因此一旦确定了S 盒的输入IN，也就确定了轮密钥RK31。

下面，利用算法结构推导出第31 轮S 盒的输入IN。

1)计算S0的输入差分Δi n0和S1的输入差分Δin1

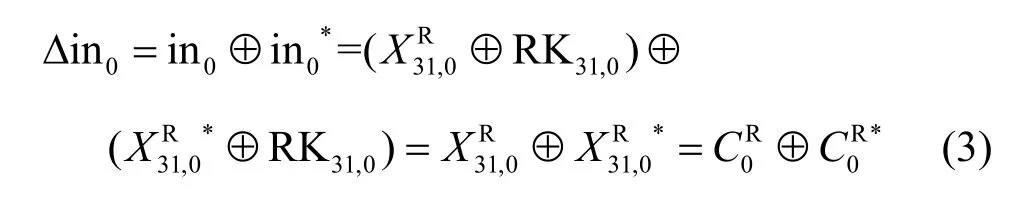
2)计算S0的输出差分Δout0和S1的输出差分Δout1

由图3 可知，故障传播到CL处时将影响它最左侧的16 bit 密文，设这16 bit 密文差分为，则

又由S2和S3不是活动S 盒可知

从而有

由此，可得关于未知量y0,y1,…,y7的16 个方程，即

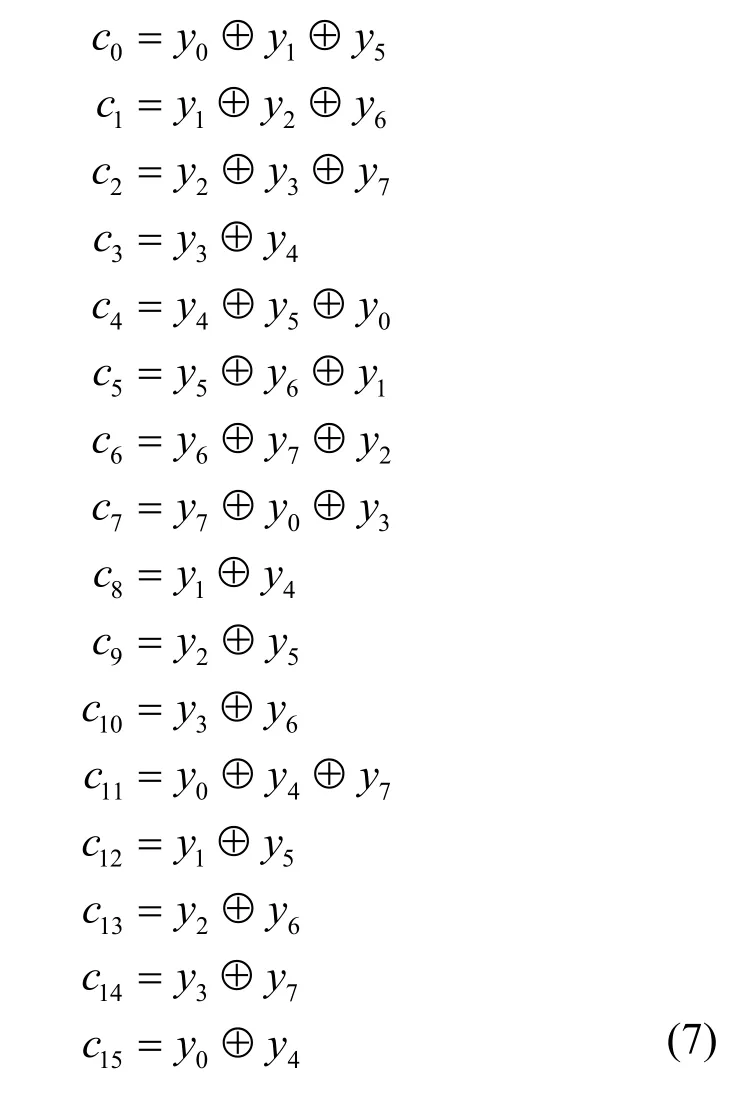
求解上述方程组，可得S0和S1的输出差分为

综上，在第31 轮引入一次单字节故障，总能够获得该轮2 个活动S 盒的输出差分。

3)求S 盒输入IN 及轮密钥

利用FeW 算法S 盒的差分特性来确定相应活动S 盒的输入，为此给出了S 盒输入输出差分对应的所有可能输入，如表3 所示。由表3 可知，对任意一对可能的输入输出差分，FeW 算法S 盒的所有可能输入至多有4 个。设第31 轮8 个S 盒的输入in0,in1,…,in7的候选值集合分别为E0,E1,…,E7，候选值个数分别为n0,n1,…,n7。首次故障引入可以使其中2 个S 盒的输入候选值个数减少到2 个或4 个。采用2 种方式来确定最终的IN。

①多次引入故障直至IN 确定

一次故障引入可以得到某2 个S 盒的输入inα、inβ的候选值集合Oα、Oβ，其中α,β∈{0,1,2,3,4,5,6,7}，将集合Oα、Oβ与Eα、Eβ分别取交集得到新的Eα和Eβ，则nα和nβ随之减小。通过不断引入新的故障，直到所有 S 盒输入候选值个数n0,n1,…,n7都为1，则此时E0,E1,…,E7中唯一的元素即可确定第31 轮S 盒的输入IN。

②利用故障攻击完成初筛，然后通过穷举计算确定最终的IN。

由表3 知，对于任意inα，首次故障引入将以较大概率使Eα中的元素减少到2 个。一旦在所有位置完成首次故障引入，即为初筛完成，此时剩余的候选值将非常少，可以通过少量的加密验证来确定最终的IN。

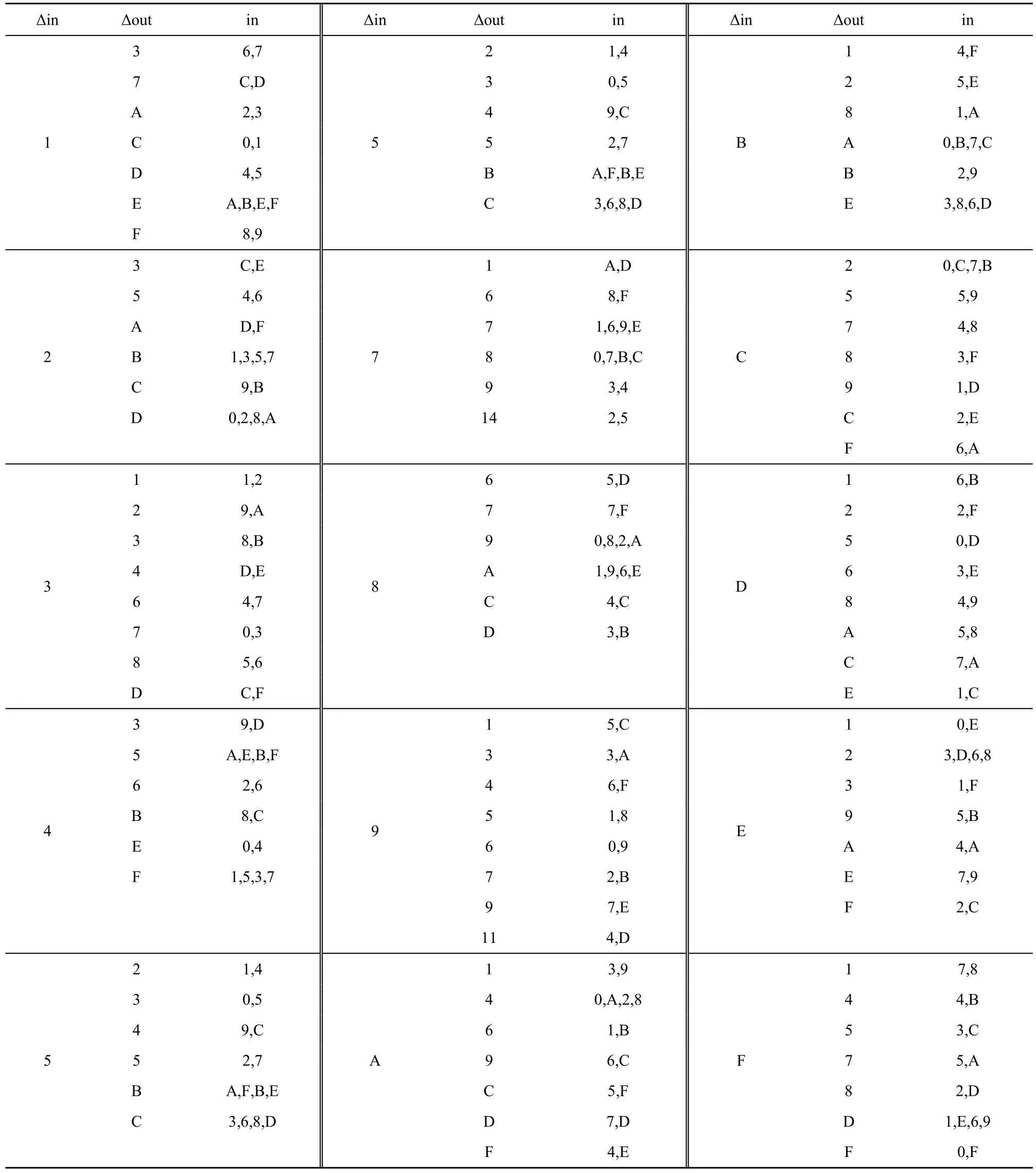
表3 固定输入差分下输出差分与输入的对应关系

设初筛完成后in0,in1,…,in7的候选值个数分别为m0,m1,…,m7，此时 IN 的可能值共有T=m0m1…m7种，故所需加密验证次数最多为T=m0m1…m7次。

确定IN 的值后，即可恢复轮密钥RK31=IN⊕CR。

3.2.2 主密钥恢复

根据FeW 的密钥编排算法，攻击者若能获得主密钥寄存器MK 的某一轮全部位置的比特值，就能通过密钥编排算法向上逆推最终获得全部主密钥。FeW-64-80 和FeW-64-128 具有不同的密钥编排算法，下面分别给出它们的主密钥恢复过程。

对于FeW-64-80，从其密钥编排算法的最后一轮向上逆推，易知密钥编排算法第58 轮MK 的值仅由RK31的25 bit、RK30的26 bit 和RK29的29 bit 共同决定。利用3.2.1 节中差分故障攻击获得RK31后，向上解密一轮，在注入故障，可恢复RK30，之后再向上解密一轮，用同样的方式可获得RK29，在此3轮轮密钥的基础上，利用密钥编排算法的逆算法即可完全恢复FeW-64-80 的80 bit 主密钥。

同理，对于FeW-64-128，易知其密钥编排算法第54 轮MK 的值仅由RK31的22 bit、RK30的26 bit、RK29的26 bit、RK28的26 bit 和RK27的29 bit 共同决定，利用3.2.1 节中差分故障攻击获得该5 轮轮密钥，即可完全恢复FeW64-128 的128 bit 主密钥。

3.3 实验仿真结果和分析

3.3.1 实验环境

硬件配置为一台PC 机（CPU 为Intel Core i5-7300HQ 2.5 GHz，操作系统64 位，内存16 GB），编程环境为Eclipse 平台下的Java 语言。

3.3.2 实验设计

恢复最后一轮轮密钥为一次完整实验，该实验过程对密钥编排算法不同的 FeW-64-80 和FeW-64-128 没有区别，但本文仍分为FeW-64-80和FeW-64-128 这2 组实验，其中明文、主密钥、单字节故障位置及故障差分值均完全随机选取。每次故障引入后，执行以下过程。

1)由3.2 节所示的攻击过程，完成对IN 候选值集合E0,E1,…,E7的筛选，故障次数加1。

2)判断IN 候选值个数n0,n1,…,n7是否均小于16，若不是，则直接返回步骤1)继续执行；若是，则对IN 恰好完成初筛，记录该故障次数为完成初筛所用的故障数，并根据此时IN 候选值个数n0,n1,…,n7计算得到本次实验所需的加密验证次数T=n0n1…n7，完成初筛后不再执行此判断。

3)判断n0,n1,…,n7是否均为1，若不全为1，则继续引入新的故障；若全为1，记录此时的故障次数即为恢复轮密钥所需的故障次数，一次实验结束。

3.3.3 实验结果

表4 展示了针对FeW-64-80 和FeW-64-128 这2 种算法各2 组（共4 组）一万次实验的结果。由表4可知，不同的密钥编排算法对单轮轮密钥恢复没有影响。因此，将4 组结果相结合作为FeW 算法单轮差分故障攻击的结论，即平均15.91 次故障引入可以恢复32 bit 轮密钥；若采用初筛后穷举的方式，则需要平均8.30 次故障引入和199 次加密验证才可以恢复32 bit轮密钥。

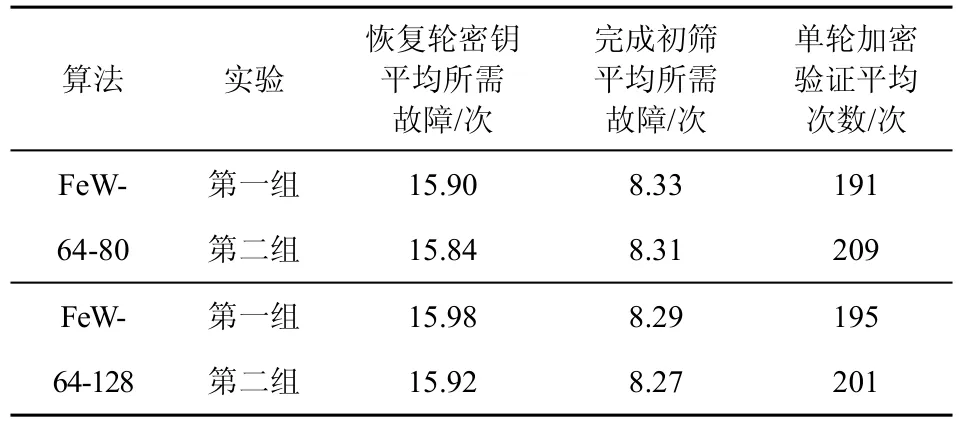
表4 2 组一万次模拟攻击结果

图4 展示了FeW 一万次实验中恢复轮密钥所需故障次数的分布情况。结果表明，大多数情况下20 次以内的故障注入即可恢复轮密钥。

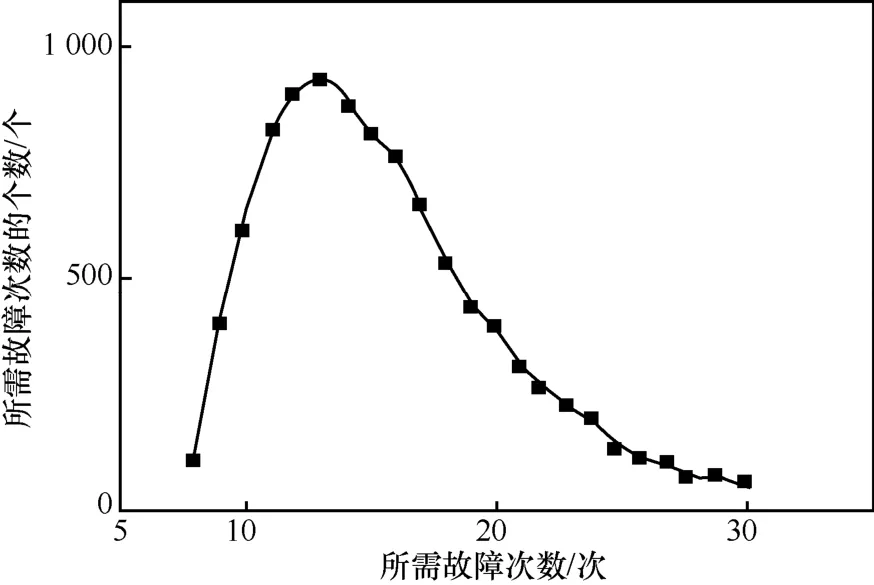
图4 Few 一万次实验中恢复轮密钥所需故障次数的分布情况

根据实验结果可知，对于FeW-64-80，平均需要15.91×3=47.73 次故障引入才可以直接恢复主密钥。若采用初筛后穷举的方式，则进行199×3=597，约 210次加密验证才可将故障次数降为8.30×3=24.90 次。

对于FeW-64-128，平均需要15.91×5=79.55 次故障引入才可以直接恢复主密钥。若采用初筛后穷举的方式，则进行199×5=995，约210次加密验证才可将故障次数降为8.30×5=41.50 次。

4 结束语

本文利用FeW 算法线性扩散函数的特点，采用差分故障对其进行了攻击。通过在第31 轮右侧输入引入单字节随机故障，较好地完成了FeW 的差分故障攻击。实验结果表明，平均需要15.91 次故障可恢复FeW 单轮轮密钥，根据FeW 的密钥编排算法，恢复80 bit 主密钥和128 bit 主密钥分别需要3 轮和5 轮轮密钥；此外，由于故障引入恢复效率的变化，本文提出了一种初筛加穷举的密钥恢复策略，结合210的穷举搜索，可将主密钥恢复平均所需故障引入次数降低一半，为同类攻击提供了新的思路。差分故障攻击对FeW 是十分有效的，为了避免此类攻击，需要对加密设备进行保护。