低轨卫星星座动态波束关闭算法

刘帅军，胡月梅，范春石，凌腾，刘立祥

（1.中国科学院软件研究所，北京 100190；2.北京中科宇航探索技术有限公司，北京 101100；3.航天东方红卫星有限公司，北京 100094）

1 引言

低轨（LEO,low earth orbit）卫星星座以星地链路时延低、传播损耗小等优点，在服务全球多媒体及物联网等业务上发挥着重要的作用。考虑到卫星链路可用带宽较小，星载发射机通常采用多波束天线配置以提供空分增益，提升系统传输效率。同时，为实现全球范围的连续无缝覆盖，需要LEO 星座的各波束间可以无缝地覆盖全球。然而，这种全球覆盖需求造成了LEO 波束间存在较大的重叠覆盖，且带来了大量无用波束的资源开销，该问题在近极轨道星座下的高纬度区域覆盖中尤其突出[1-2]。例如，近极轨道LEO 星座——铱星（Iridium）系统，为避免相邻卫星多波束间在高纬度区域产生严重重叠，该系统采用动态波束关闭策略，降低系统运行过程中的相互干扰，并节省星上功率等资源开销。相关文献指出，铱星系统在实际运行过程中仅需2 150 个波束（关闭1 018 个波束）即可满足覆盖全球的通信业务[3]。

低轨星座网络动态波束关闭策略是在多波束低轨卫星星座场景下确定卫星多个波束如何关闭的策略，需在既定目标和约束下从给定波束集合中选择一组波束进行关闭。针对该问题，国内外航天机构开展了相关研究。文献[4]提出了一种全球低轨星座系统中的动态波束关闭方法，主要考虑了在星载太阳能帆板充放电约束下的波束开关策略，通过地基控制中心集中调度以最大化卫星功率利用率。文献[5]提出了一种干扰抑制技术，综合考虑了低轨星座内波束重叠、负载轻重等因素，通过确定第一卫星第一波束覆盖带而关闭剩余波束，同时由第二卫星第二波束子集进行补充覆盖，在满足全球连续覆盖下可降低星座内的干扰并优化负载均衡。与文献[5]类似，文献[6-7]提出了通过动态波束关闭实现低轨星座频率规避的方法，重点考虑了与地球同步轨道（GSO,geosynchronous orbit）卫星的干扰规避问题。

现有研究以顶层策略为主，即仅定义或约束一些波束关闭的原则，尚未进行严谨的数学模型建立及动态波束关闭算法的深入研究。在此基础上，本文建立低轨星座网络动态波束关闭的系统场景及数学模型，并在给定目标函数和约束条件下建立、求解优化问题。本文首先对低轨星座网络动态波束关闭的系统场景和数学模型进行建模，在保证全球连续无缝覆盖和有业务传输的波束不关闭这2 项约束条件下，建立了旨在最小化低轨星座激活波束个数的最优化问题，从而最小化由波束间重叠所造成的干扰与资源闲置。然后，通过将待求解的最优化问题转化为集合覆盖问题（SCP,set cover problem），阐明了该问题的NP 完全属性；结合低轨星座网络动态运行特点，急切需要一种快速收敛且高效的探索式算法。基于此，本文提出一种门限控制截断的探索式算法，其基本思想是在给定时间域内进行探索，以保证高动态低轨星座网络下的快速收敛特性。最后，仿真结果以实际低轨星座网络——铱星系统为仿真场景，验证了所提算法在降低波束重叠方面的效果。

本文主要工作归纳如下。

1)建立了低轨星座网络动态波束关闭的数学模型。基于低轨星座卫星动力学方程、星上波束配置、星座覆盖要求等约束，以最小化星座激活波束个数为目标，建立了低轨星座网络动态波束关闭的最优化模型。

2)提出一种基于门限控制截断的探索式算法。对动态波束关闭优化问题进行转化与分析，证明了该问题是NP 完全问题；结合低轨星座对地覆盖的高动态特性，提出了具有时效性的基于门限控制截断探索式算法。

2 系统模型与问题建模

2.1 LEO 卫星星座场景描述

本文以低轨多波束卫星星座为研究对象，该星座网络内各星采用星载多波束天线。记该低轨星座的卫星个数为NS，星座内卫星为si,i=1,2,…,NS。对于每颗卫星而言，采用半长轴、偏心率、轨道倾角、升交点赤经、近地点幅角和近地点时刻这6 个参数即可实现卫星位置与运行规律的表征。为了更清晰地表征星座网络的空间关系，定义卫星本体坐标系[8-9]：以卫星平台质心为坐标原点O，以原点指向地心为正Z轴，以原点指向卫星切线运行方向为正X轴，根据右手法则得到Y轴。卫星本体坐标系如图1 所示。

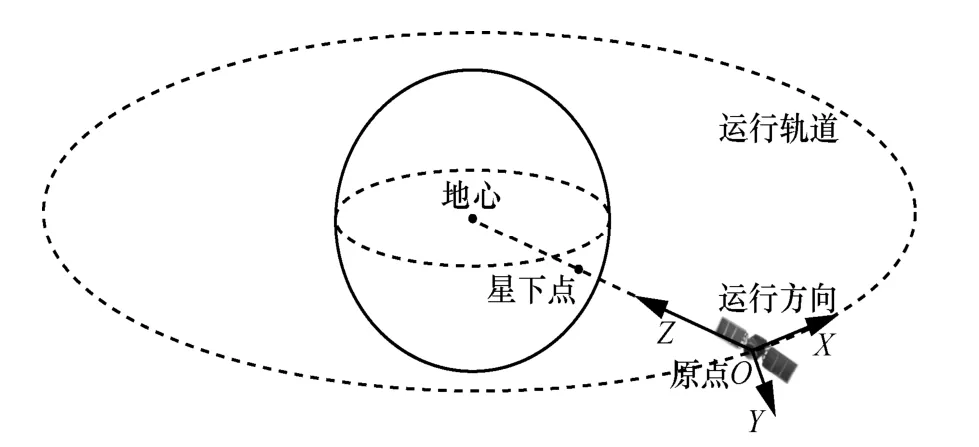
图1 卫星本体坐标系

记每颗卫星的波束个数为NB，bi,j表示卫星si的第j个波束，i=1,2,…,NS,j=1,2,…,NB，则系统总波束个数为NB,tot=NSNB。记星座网络的目标覆盖区域为G，对于任意终端gk={Latgk,Longk}而言，若该终端位于服务区域内，则表示为gk∈G；否则表示为gk∉G。

卫星多波束通过星载多波束天线生成，即多波束空间指向与卫星平台自身密切相关，基于此，卫星多波束空间指向的定义需以卫星本体坐标系为参考。对于波束bi,j而言，其在卫星si本体坐标系下，定义其空间指向，其中，Azi,j为方位角，Eli,j为仰角。方位角定义为以正X轴顺时针方向到波束指向在XOY平面投影的角度，仰角定义为波束指向与XOZ平面的夹角。同样，可求得在卫星si本体坐标系下卫星si指向终端gk的方向为。进一步，通过式(1)可获得空间向量对应的OXYZ表示，即。

此时，波束指向与卫星终端指向的空间夹角θi,j,k如式(2)所示。

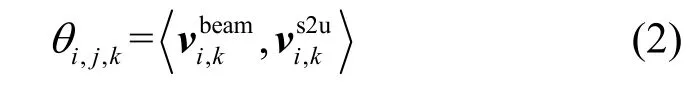
其中，θi,j,k可根据空间角度关系计算得到。卫星多波束指向示意如图2 所示。

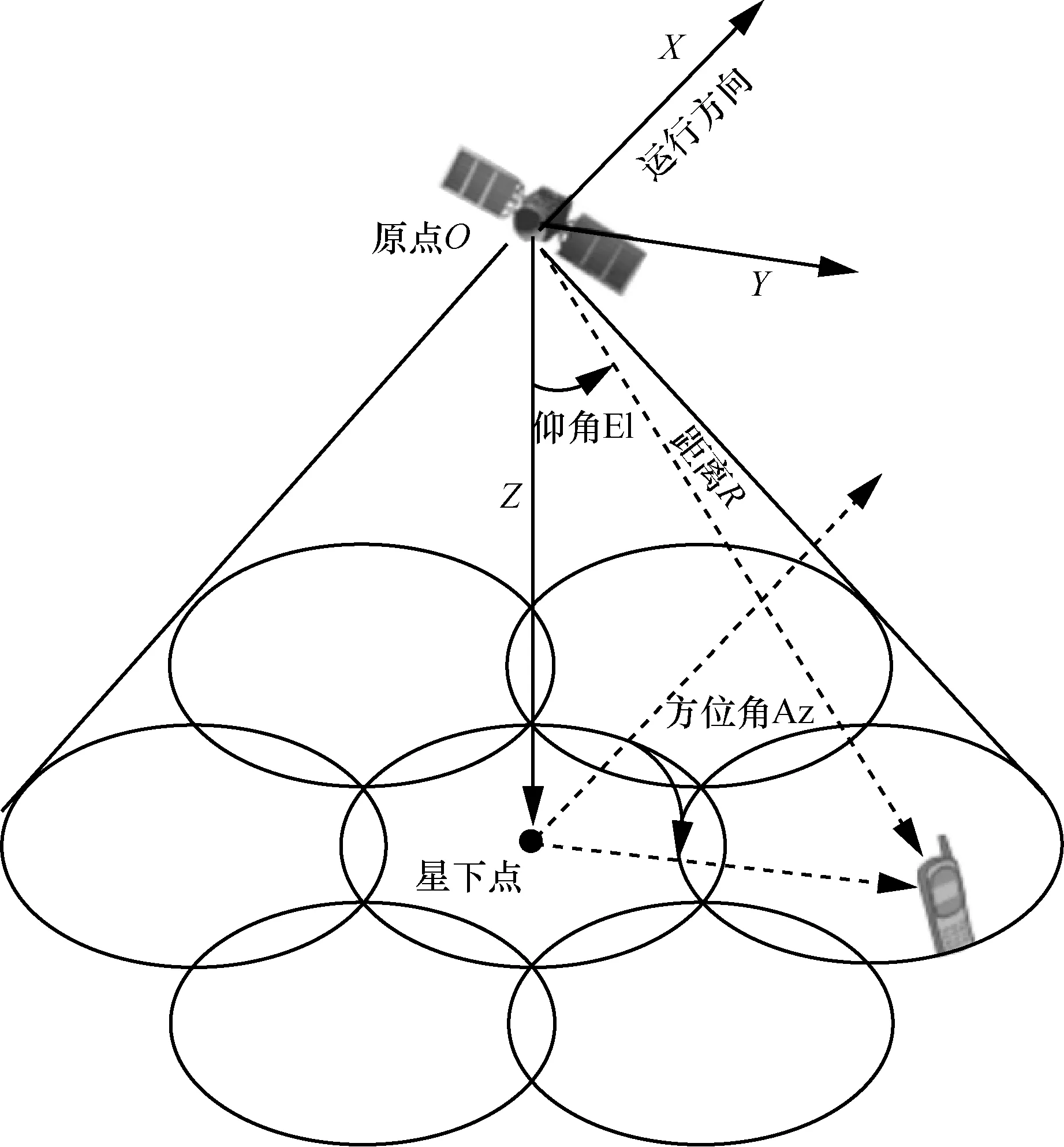
图2 卫星多波束指向示意

卫星各波束采用圆波束模型，对应的波束角（BW,beam width）记为。对于采用具有其他非圆波束的星座网络而言，也可通过求解终端与星间相对空间角度判断覆盖与否。对于波束bi,j、终端gk而言，当卫星终端指向与波束指向之间空间夹角小于该波束半波宽时，认为终端被该波束覆盖，否则认为该终端不在波束覆盖范围内。为此，定义终端-波束相关的覆盖因子ci,j,k，表征终端gk是否被波束bi,j覆盖。覆盖因子ci,j,k的计算式为

同时，定义波束激活与否因子ai,j，以表征波束处于激活或关闭的状态。ai,j计算式为

2.2 问题建模

本文研究目标是最小化星座网络工作的波束数，如式(5)所示。

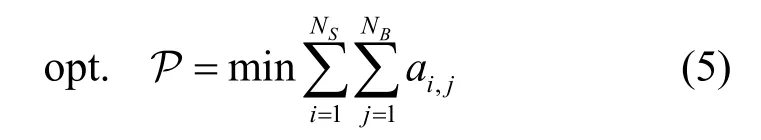
当星座网络内部分波束关闭时，应满足如下2个约束条件。

约束1保证服务区域的覆盖，即在若干波束关闭的情况下，对于服务区域内任意终端而言，至少存在一个激活的波束可覆盖该终端。该约束为

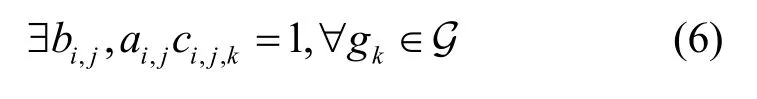
约束2若有正在进行业务传输的波束不可关闭，不妨将此波束集合记为 Bserving，Bserving⊂B。该约束为

综上，本文研究的动态波束关闭最优化问题为

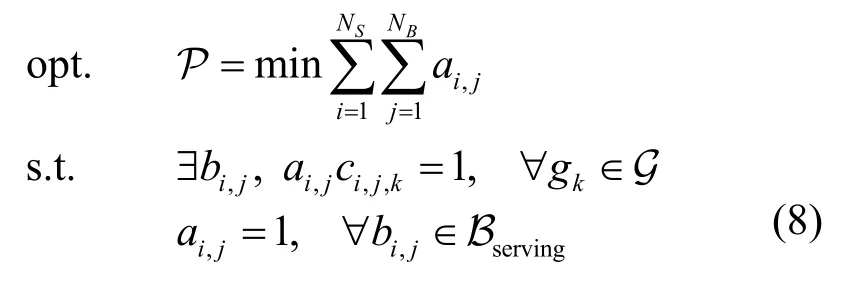
3 门限控制截断的动态波束关闭算法

本节描述了所提门限控制截断的动态波束关闭算法。首先对式(8)中的优化问题进行分析和转化，进而设计所提算法。

3.1 问题分析与转化

考虑到式(8)所建立的最优化问题属于二重求和问题，目标是最小化激活波束的个数，而约束需保证连续覆盖与有业务传输波束不关闭。由此，可将此二重求和重写为以波束为基的一重求和问题。

构造波束与终端相关的一个矩阵D，该矩阵的行表示一个波束，列表示终端，如式(9)所示。

记dn为矩阵D的行向量，任意若干组行向量组成子矩阵，则最优化问题(8)可转化为求解一个最小SCP，如式(10)所示。

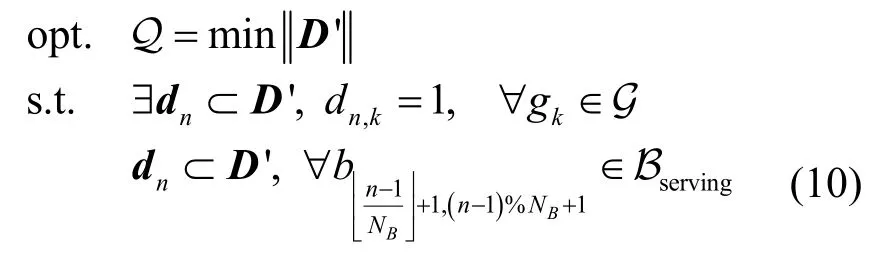
以下将阐明2 个引理，以证明本文所求解动态波束关闭问题（即式(8)）是一个NP 完全问题。

引理1式(8)的优化问题P 等价于式(10)的优化问题Q。

证明由式(9)可知，矩阵D是由覆盖因子ci,j,k组成的二维矩阵，而最优化问题Q 目标是最小化子矩阵D'的行向量个数，即最小化波束个数；优化问题Q 的约束1 保证了子矩阵中至少存在一个行向量（即波束），可满足对覆盖区域G 内任意终端的覆盖；进一步结合由式(9)对矩阵D的定义可知，优化问题Q 的约束2 保证了正在进行业务传输的波束处于激活状态。综上，优化问题Q 在目标函数与2 个约束条件上与优化问题P 是一致的，即式(8)的优化问题P 等价于式(10)的优化问题Q。

证毕。

引理2式(10)的优化问题Q 是一个最小SCP。

证明SCP=(X,Y,W)描述为给定一个全集X及该全集的若干子集Y，有∪∀y∈Y=X，记子集Y内每个元素的权重为w(y)，则目标是找出一个集合F⊆Y，在满足全集X所有元素下，∪∀y∈F=X，使该集合权重和最小，即。结合优化问题Q，可将其建模为一个SCP 实例，具体如下。令X={k|k=1,2,…,K}，Y={yn|n=1,2,…,NB,tot}，且有yn={k|dn,k=1}，由星座内所有波束可对区域G 内终端全覆盖可知，∪∀y∈Y=X，且w(y)=1。综上，优化问题Q 是一个最小SCP。

证毕。

结合上述2 个引理，可给出如下定理及证明。

定理1式(8)的优化问题P 是NP 完全问题。

证明由引理1 可知，式(8)优化问题P 等价于式(10)优化问题Q；由引理2 可知，式(10)优化问题Q 是一个最小SCP；同时，SCP 是已知的NP 完全问题[10-12]。综上可知，本文待求解的动态波束关闭优化问题P 是NP 完全问题。

证毕。

3.2 门限控制截断探索式算法

由3.1 节可知，本文待求解的问题是一个最小SCP。针对此问题的求解方法可分为精确求解方法和启发式求解方法。考虑到SCP 的NP 完全属性，使用精确求解方法虽然可以保证得到最优解，但随着求解问题规模的不断扩大，精确求解方法的求解时间呈指数上升，此时无法保证在可接受的时间内返回一个候选解。相比而言，启发式方法在合理的求解时间内能够获得一个尽可能好的候选解，但是不能保证这个候选解是最优解。考虑到本文所求问题的规模较大，例如，对于铱星系统的3 168 个波束，终端全球分布取1 经度×1 纬度情况下，则需求解矩阵为3 168×64 800 的规模；对于OneWeb 系统，则需求解矩阵为11 520×64 800 的规模，精准求解方法求解时间开销难以接受。

基于此，本文给出一种门限控制截断的探索式算法，基本思想是在保证全覆盖与某些波束不关闭的约束下，逐次尝试关闭波束；为保证算法的时效性，采用了门限控制的方式以截断执行时间窗。在每次执行过程中选择哪个波束进行关闭则是本文算法的难点。首先，给出本文算法执行的总体流程设计；然后，详述算法过程中关闭波束选择的设计。

1)门限控制截断探索式算法总体流程设计

门限控制截断的探索式算法基本流程如下。

步骤1令波束-终端相关的覆盖矩阵D'=D，且在D'中选择一个行向量dn，将此行向量从矩阵D'中去除（即等价于关闭行向量dn所代表的波束）；令Niter=0。

步骤2若D'仍满足式(10)中的约束条件，则更新D=D'，返回步骤1 继续执行；否则，迭代搜索次数Niter加1，跳至步骤3。

步骤3判断迭代搜索次数是否超过门限，即Niter＞NTh，若满足，跳至步骤4；否则，返回步骤1。

步骤4算法结束，输出波束关闭算法的解D。

2)关闭波束选择的设计

关于步骤1 中“在D'中选择一个行向量dn”，选择dn的依据如下。

原则1有正在进行业务传输的波束不关闭。

原则2重叠覆盖最严重的波束应优先选择关闭。对该波束所覆盖的终端而言，其波束平均覆盖重数（同时被波束覆盖的次数）最大的将被优先选择以关闭。因此行向量dn的选择方法如式(11)所示。

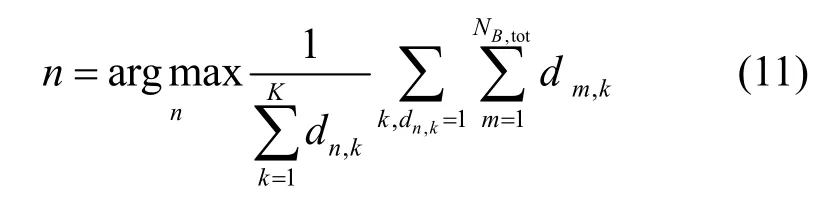
4 仿真结果与分析

4.1 仿真配置

以铱星星座网络为仿真场景，铱星星座空间段为66 颗星，每颗星具备48 个点波束，则铱星星座网络波束个数总计为66×48=3 168。铱星星座的仿真参数配置[13-14]如表1 所示。

表1 仿真参数配置

铱星采用星载三幅相控阵天线，每副天线生成16 个点波束。考虑到卫星实际48 波束的波束宽度及指向等并未公布，基于铱星星座终端最小工作仰角8.2°等参数，本文仿真场景采用表2 中的点波束配置。

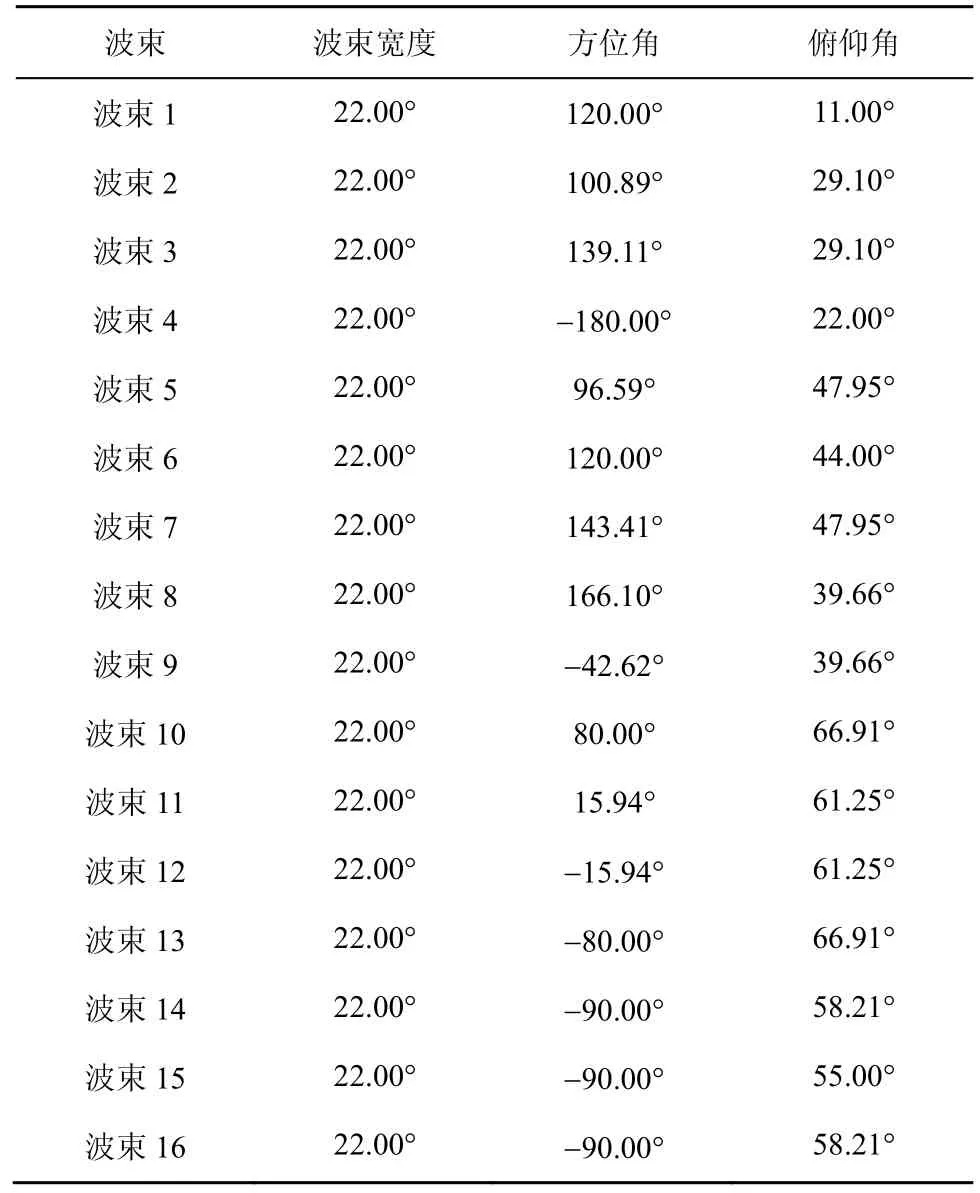
表2 铱星单幅相控阵天线16 波束仿真配置

其余两幅相控阵生成的32 副天线，只需在上述天线基准上分别顺时针和逆时针旋转120°即可。通过仿真可以得到48 波束配置下的单星覆盖区域仰角及多波束分布特性，如图3 所示。其中，纬度的正值表示北纬，负值表示南纬；经度的正值表示东经，负值表示西经。图3(a)为终端对卫星的仰角分布。从图3(a)可以看出，处于卫星星下点区域的终端仰角较大，星下点处终端对卫星的仰角为90°；随着终端位置远离星下点，仰角越来越小，卫星对单颗终端的覆盖可实现最小工作仰角8.2°，与铱星网络工作参数一致。图3(b)为星载48 波束对地覆盖，不同颜色表示48 个波束的对地覆盖区域。由于本文假设同一波束宽度的圆波束配置，因此，星下点附近的波束覆盖范围较小，远离星下点区域的波束覆盖范围较大。

4.2 结果与分析

通过仿真可知，铱星星座网络可关闭1 255 个波束，仅1 913 个波束同时工作即可满足全球覆盖要求，即本文所提方案可节省39.61%的波束资源。铱星星座网络波束全部激活情况下对地覆盖分布如图4 所示。采用本文波束关闭策略后，铱星星座网络对地覆盖分布如图5 所示。

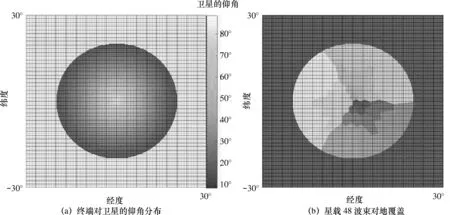
图3 卫星覆盖区域仰角及多波束分布

由图4 可以看出，铱星星座对地覆盖在赤道与中低纬度区域较稀疏，而在极地区域及高纬度区域较密集。对于任意终端而言，至少有一个波束的覆盖保证了网络的全球覆盖，而极地区域存在多达15 个波束重叠覆盖。相比而言，当采用波束关闭策略后，极地区域可在保证全球连续覆盖的情况下，降低至最多7 个波束重叠覆盖。图4 和图5 的覆盖分布可进一步通过波束覆盖重数的累计分布函数（CDF,cumulative distribution function）来表征，如图6所示。

图4 铱星星座网络波束全部激活情况下对地覆盖分布

图5 铱星星座网络采用波束关闭策略后对地覆盖分布

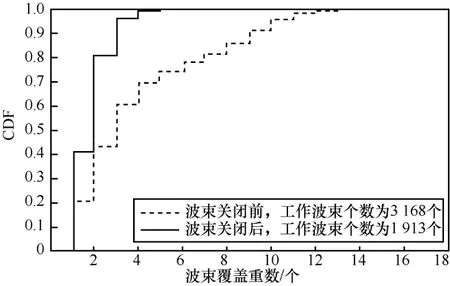
图6 铱星星座网络波束覆盖重数CDF

由图6 可知，波束关闭前，有超过80%的终端具备至少2 个波束重叠覆盖；采取波束关闭策略后，该比率下降到60%。波束关闭前，39%的终端超过了3 个波束重叠覆盖；采取波束关闭策略后，该比例下降到3%。由此可看出，波束间重叠覆盖的问题得到显著改善。进一步地，探究卫星工作波束个数与卫星工作纬度的关系，如图7 所示。其中，纬度的正值表示北纬，负值表示南纬。

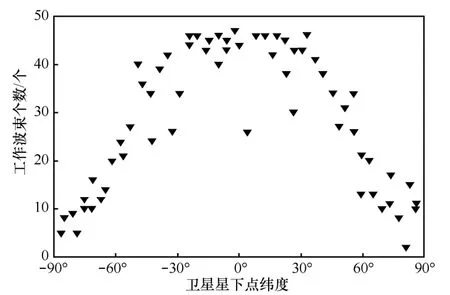
图7 波束关闭策略后激活波束个数与星下点纬度的关系

由图7 可知，对于运行在中低纬度上空的卫星而言，波束工作的个数较多，如纬度低于40°区域内，卫星工作波束个数在40 个以上，即仅关闭了不到8 个波束；对于运行在高纬度上空的卫星而言，波束工作的个数较少，如纬度高于75°区域内，卫星工作波束个数大多在10 个以下，即关闭了38 个波束。

综上，针对星座网络在高纬度区域重叠覆盖严重的问题，本文采取的波束关闭策略可显著降低高纬度区域重叠波束覆盖，在保证全球覆盖的基础上最小化星座系统的工作波束个数，在降低波束间干扰的同时降低了39.61%的波束资源开销。

5 结束语

针对低轨多波束卫星星座网络存在的波束间严重的重叠覆盖问题，本文建立了波束关闭优化问题，在阐明该问题的NP 完全特征后，采用探索式方法进行求解。以铱星星座网络为仿真场景，对于系统内3 168 个波束仅需1 913 个波束同时工作即可满足要求，降低了39.61%波束资源的开销。下一步工作主要包括考虑非正圆波束形状下的动态关闭方法，如高椭圆波束及其他成形波束；考虑在对GSO 卫星干扰规避下的动态波束关闭方法。