大规模MIMO 系统中基于谱分离的导频去污染

王海荣，董健，王玉辉

（1.南京邮电大学通信与信息工程学院，江苏 南京 210003；2.中通服咨询设计研究院有限公司，江苏 南京 210019；3.南京船舶雷达研究所，江苏 南京 211100）

1 引言

随着经济全球化及互联网技术与移动通信技术之间的不断融合发展，未来将会是移动互联网的时代。在接下来的10 年中，数据传输速率将达到10 Gbit/s，无线数据流量将面临1 000 倍的增长[1]，在此驱动下，第五代移动通信技术（5G）得到了充分的发展。但如果5G 技术仅仅是当前4G 技术的一个简单演进，可能无法满足这1 000 倍的无线速率的增长，显然，需要具有突破性的技术。massive MIMO[2-4]（又称为“large-scale MIMO”或者“大规模天线系统（LSAS,large-scale array system）”）将是5G 中提升频谱效率的关键技术之一。massive MIMO 技术以其相对直观地提高系统容量的方式成为当前的研究热点[5-7]。massive MIMO 是指在基站端配置超过100 根且少于1 000 根天线，即每个基站都有一个大规模的天线阵列，可以同时服务大量的用户。大规模的天线可以带来以下优势：简化了多用户的处理，随着天线数的大量增加，采用诸如最大比合并发射和迫零预编码等线性处理方法就足以获得非常接近复杂编码如脏纸编码算法的最优性能；显著降低上下行链路的发射功率，符合未来以降低能源消耗和保护人类生存环境为目标的“绿色通信”的要求[8-10]；同时可以很好地消除热噪声和快衰落效应。

虽然采用massive MIMO 技术能获得巨大性能增益，但还是依赖于实际收发机的设计。要实现下行链路的多用户预编码和上行链路的多用户检测，基站都必须获知全部或者部分的信道状态信息（CSI,channel state information）。但是，基站处天线数目的大量增加，会导致无法沿用传统的信道状态信息反馈模式，这是因为传统的CSI 反馈量是会随着天线数目线性增长的，当天线数量巨大时，反馈所需的时间将会远远大于信道相干时间。所以，当前的massive MIMO 技术多应用于时分双工（TDD,time division duplex）系统中，利用信道互易性来获得信道状态信息[2-4]。由于在TDD 系统中信道状态信息是依靠上行导频信号估计的，而导频信号空间的维数总是有限的，因此在未来的稠密多小区多用户TDD 系统中，不可避免地总是存在多个小区的用户采用相同导频同时发射，从而导致基站无法区分本小区用户的导频来获得足够精确的信道状态信息，形成所谓的“导频污染”（pilot contamination）[2,4,11]，这已成为massive MIMO 技术新的性能瓶颈。

针对导频污染问题，现有文献已经给出了大量理论研究和减轻导频污染的方法[12-17]。比较值得注意的是Müller等[18]所提出的盲导频去污染，他们指出导频污染并不是massive MIMO 技术所固有的问题，而是因采用线性信道估计方法所导致的，通过适当地设计系统参数，利用发射功率控制及切换，以及接收信号协方差矩阵渐近谱中有用信号、干扰信号及噪声信号彼此可分离的特性，可以构造一个完全没有导频污染的massive MIMO 多小区系统。但要实现这一目标，目前来看还是很复杂的，比如各个参数应当满足怎样的条件，以及参数之间有着怎样的关系都还没有非常清晰的表述。另一方面，大维随机矩阵谱分析理论也在不断发展，Bai等[19]早在1998年就证明了没有特征值位于大维样本协方差矩阵的极限谱分布支撑集之外，这是谱分离理论的基础。进一步地，文献[20]在1999 年证明了大维样本协方差矩阵的特征值是可以精确分离的。近年来，Mestre[21]给出了不同采样维度下大维样本协方差矩阵特征值的渐近密度，随着采样维度的增加，该密度会集中到特定的几个特征值周围。Couillet等[22]在感知无线网络中利用大维随机矩阵理论中的谱分离和特征推断来估计多个信源的发射功率。Paul 等[23]进一步证明了没有特征值位于可分离协方差矩阵的极限经验谱分布支撑集之外。Couillet等[24]和Wen等[25]则利用大维随机矩阵谱分析的相关理论分别给出了高斯和非高斯相关MIMO 多接入信道的确定等价式。

本文考虑采用massive MIMO的多小区TDD系统。利用大维样本协方差矩阵特征值分布函数的几乎确定收敛性，得到了当噪声方差σ2一定时，基站接收信号的样本协方差矩阵渐近谱中有用信号、干扰信号以及噪声信号可分离条件首先取决于f0和P（用户上行发射功率），之后才与f相关。其次，在f0和P的取值能保证实现谱精确分离的前提下，给出了当f＜ 1时，系统参数的一个设计方法，使盲导频去污染更趋实用。

本文使用的符号及其含义如下。(A)T表示矩阵A的转置，(A)*表示矩阵的共轭，(A)†表示矩阵的共轭转置；tr{A}表示矩阵的迹，det(A)表示矩阵的行列式，表示矩阵的Frobenius范数，E{·}和var{·}分别表示期望和方差，IN表示N阶单位矩阵，CN(0,1)表示均值为0、方差为1的高斯分布，z∈C+表示{z∈C,ℑ[z]＞0}，mF(z)表示分布F的Stieltjes 变换。

2 系统模型

考虑一个由L个小区组成的massive MIMO 多小区多用户TDD 系统，假设各小区之间时间同步全频谱复用，每个小区基站配置M根天线，同一基站的M根天线所组成的天线阵列足够紧凑，对特定的发射天线有着相同的大尺度衰落。第j小区的单天线用户数为nj(nj≤M)，且有。小区内的导频正交，小区间的导频则完全复用。那么目标小区基站接收到的上行信号为

其中，Hj是M×nj的矩阵，表示第j小区的nj个发射天线到目标小区基站天线阵列的小尺度衰落因子，其所有元素是独立同分布的（IID,independently and identically distributed）且满足CN(0,1)；Dβj是nj×nj对角矩阵，对角元素为βj=[βj1,；pr表示每根天线的平均发射功率；为第j小区nj根发射天线所用的导频向量，τ为用户发送的导频训练序列长度，而且Ψj中元素独立且也满足均值为0、方差为1。W表示M×τ的加性噪声满足CN(0,1)，σ表示噪声标准差。进一步地，令，为了后续推导方便，设同一小区内Pj的nj个对角元素相同，都为Pj。那么式(1)可以表示为

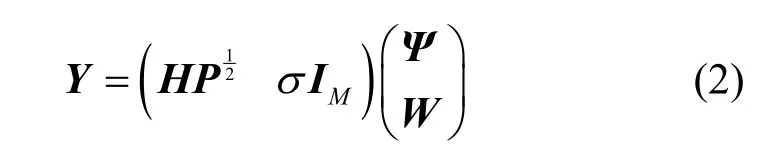
3 渐近谱分析

由于H满足其元素是独立且有有限四阶矩，根据文献[26]中的定理3.1 可知，若M，n1,…,nK→∞且，那么HPH†的经验谱分布（ESD,e mpirical spectral distribution）弱且几乎确定收敛到一个极限分布G。对于z∈C+，分布G的Stieltjes变换mG(z)是关于mG的方程具有正虚部的唯一解，如式(5)所示。

因此，HPH†中ESD 的几乎确定收敛性保证的几乎确定收敛性，同时可以得到的ESD 几乎确定收敛到一个分布H，对于z∈C+，其Stieltjes 变换mH(z)满足式(6)所示条件。

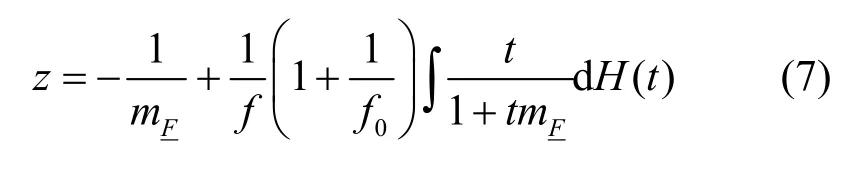
因此得到了与文献[18]不一样的结论。文献[18]中给出的可分离条件认为当功率矩阵P、噪声方差σ2确定后，分布的可分离特性是由确定的，即f、f0对最终可分离特性的影响是同等的，可以互相补偿来实现谱的精确分离。但是由前文的推导发现，f、f0对极限谱分布最终可分离特性的影响不同的，即具有不同的优先等级。分布F的可分离特性首先是由分布H的可分离特性来保证的，而分布H的分离特性是由极限分布G的分离特性确定的。也就是说，当f0的取值无法保证分布G的分离特性时，无论如何调节f，都是无法获得分布的分离特性的；而当分布G是分离时，f的大小才对分布的分离特性有影响。归纳起来，可以描述如下。

4 实现导频去污染的分层参数设计方法

由第3 节的分析可知，实现massive MIMO 系统中导频去污染的可分离条件应当是分层实现的：首先考虑分布G的分离特性和f0的关系，然后考虑f对分布的分离特性的影响。

4.1 分布G的分离特性和f0

形如HPH†的样本协方差矩阵的极限分布G的谱分离特性是通过对分布G支撑集的划分来构建的。文献[26-28]对此有较为详尽的分析，本文引用文献[28]中的定理，如定理1 所示。

定理1令集合，其中是分布G的支撑集SG的补集，并且xG是定义在B上的函数，满足

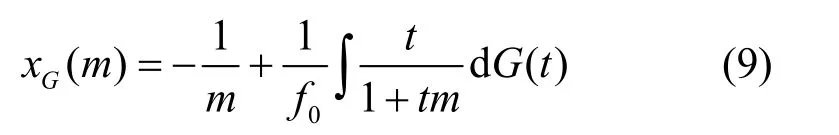
对x∈R*，能确定mG(z)的极限m0(x)，在z→x时，遵循以下规则。

规则1如果x∈SG，那么m0(x)是关于虚拟变量m的方程x=xG(m)在B上唯一有正虚部的解。

规则 2如果，那么m0(x)是使的关于虚拟变量m的方程x=xG(m)在B上唯一的实数解。反之，对m∈B，如果，那么。

由规则2 可以很容易地确定分布G的支撑集，即

考虑本文的分布G和式(9)，则有

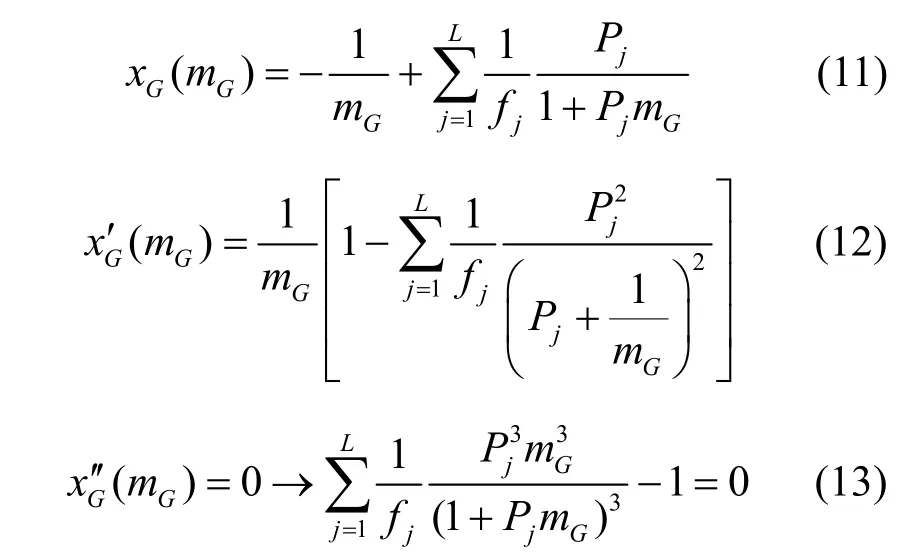
考虑以下情况：当L=3，(P1,P2,P3)分别为(5,3,1)和(8,3,1)，f0=10，f1=f2=f3时，那么函数xG(mG)和分布G的支撑集分别如图1(a)和图2(a)所示。由这 2 个图可知，当函数xG(mG)递增时，xG(mG)不在分布G的支撑集之内。对于不同的(P1,P2,P3)取值，分布G的支撑集会被划分为LG≤L块，当LG=L时，(P1,P2,P3)对应的每一个特征值都是精确分离的；当LG＜L时，有对应的特征值混叠在一起。结合前文的渐近谱分析，可以分别得到对应于图1(a)和图2(a)的经验谱和渐近谱的分布，如图1(b)和图2(b)所示。从这2 个图可以看到的谱分离性与分布G的支撑集的分离性是完全对应的。

具体来看，图1(a)中的圆圈表示局部极值点，是成对出现的，表示为；方块表示拐点，表示为mG,j，其中j=1,…,LG，LG≤L；粗实线表示的是分布G的支撑集。图1(b)中是对应的的渐近谱和经验谱密度，其中，虚线表示渐近谱，柱状图表示经验谱（经验谱实验中取N=120），为了考察f0对分布G可分离性的影响，本文实验取f=100，图2 标识同图1。

图1 分布G的支撑集分离特性与的谱分离性对应关系（不完全分离）

图2 分布G的支撑集分离特性与的谱分离性对应关系（完全分离）

此外，由图1 和图2 中局部极值点和拐点与分布G的支撑集的关系可以发现，成对出现的极值点对应右侧一段支撑集，如图1 和图2 中的所示（其他极值点省略未标出）；而在每对局部极值点之间总有一个拐点，如图1 和图2 中的之间有拐点mG,1所示（其中，在图中未标出），因此根据式(10)～式(13)，可以得到一个判定相邻特征值是否精确分离的条件，如命题 1所示。

命题1当满足

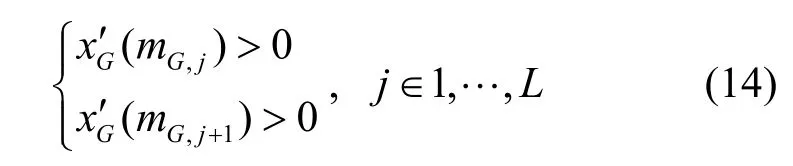
本文给出一个直观的判定条件，并不进行证明，相关的严格数学推导参见文献[26-27]。根据命题1，可以得到如图3 所示的对应于f0和的可分离区域。由图3 可以得出对应于图1和图2 的2 个点分别是。很明显位于可分离区域外而位于可分离区域内，这与图1 和图2 所示的结果是相符的。

图3 对应于 f0和的可分离区域

由图3 也可以看到，当期望信号与干扰的功率差异越大时，f0的设计越简单，而两者功率很接近时，区分彼此则是很困难的。然后，与特征推断中需要把每一个对应的特征值都精确分离不同，当实现盲导频去污染时，只需将期望信号与左右相邻最近的干扰信号精确分离出来即可，其他离得更远的干扰源的多少并不会影响最终分离的结果。最后还发现，当对应特征值的分离性存在时，期望信号的功率并不一定要大于干扰信号功率，以图2 为例，一般考虑功率值为8 时对应期望信号功率，而为1 和3 时是干扰信号功率。但当假设期望信号功率为3，干扰信号功率为1 和8 时，往功率值为3 的对应子空间投影和往功率值为8 时的子空间投影几乎是没有什么区别的。

4.2 分布的分离特性和f

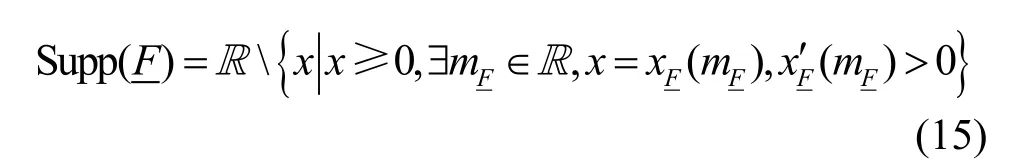
F的支撑集是无法实现的。至今，关于这个问题仅有一个充分条件在文献[22]中被提出，该充分条件假设了f≥ 1。这对于实际系统设计而言，无疑是不可行的，因为f≥ 1意味着在大规模MIMO 系统中所采用的导频长度要大于或者等于基站的接收天线数。

命题 2为了求解式(15)中的支撑集，都可以通过mG来计算。

证明由式(8)可以看到对于每一个给定的值，还与mH相关，由式(6)可知，mH可以通过mG来计算，所以显然是可以通过mG来计算的。对于则没那么简单，首先对式(8)求导得到

其中，有

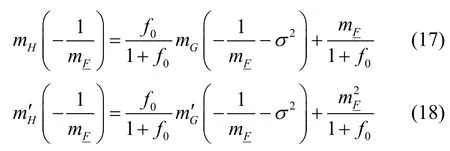
显然，式(17)可以通过mG直接计算获得。而式(18)则没那么直接，需要知道的表达式，直接对式(5)求导来计算是困难的。但利用反函数的导数就等于原函数导数的倒数这一结论，则很容易就能得到式(19)。

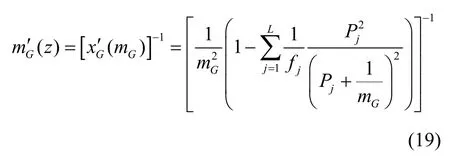
证毕。

算法1对给定的f(f≤1)，判断是否位于分布的支撑集之外

2)求解关于mG的方程。

5 仿真结果

本节通过数值仿真来评估本文所提的分层参数设计方案来实现massive MIMO 系统中的导频去污染。由于本文研究的是盲导频去污染的分层参数设计方案，因此数值仿真关注的是所提方案的有效性，实现渐近谱可分离后，对通信系统性能（BER,bit error ratio）的对比与文献[18]是类似的，因此本文不再赘述。不失一般性地，设L=3，σ2=0.1。依据分层参数设计首先要确定f0的值，假设(P1,P2,P3)=(8,3,1)，那么对于massive MIMO系统而言，f0=10是一个典型值。由图3 可知，位于可分离域内。接下来就需要寻找最小的参数f，使其能满足的谱精确分离。由于要使得f∈(0,1)，很自然想到用二分法来搜索可能的f。对每一个可能的f值可采用4.2 节中的数值算法来验证其是否支持G和的支撑集分离性。对于上述的设定：σ2=0.1，(P1,P2,P3)=(8,3,1)，f0=10，f1=f2=f3，可以最终搜索得到最小的f值为0.5（搜索步长为0.1），这是一个实际系统可以接受的参数值，如图4 所示。图4中右侧纵轴表示的支撑集，而下侧横轴表示的支撑集。对应的的渐近谱和经验谱密度分布如图5 所示，其中虚线表示渐近谱，柱状图表示经验谱（经验谱实验中N=120）。可以看到其谱的分离性与图4 中分析的支撑集分离性是相一致的。

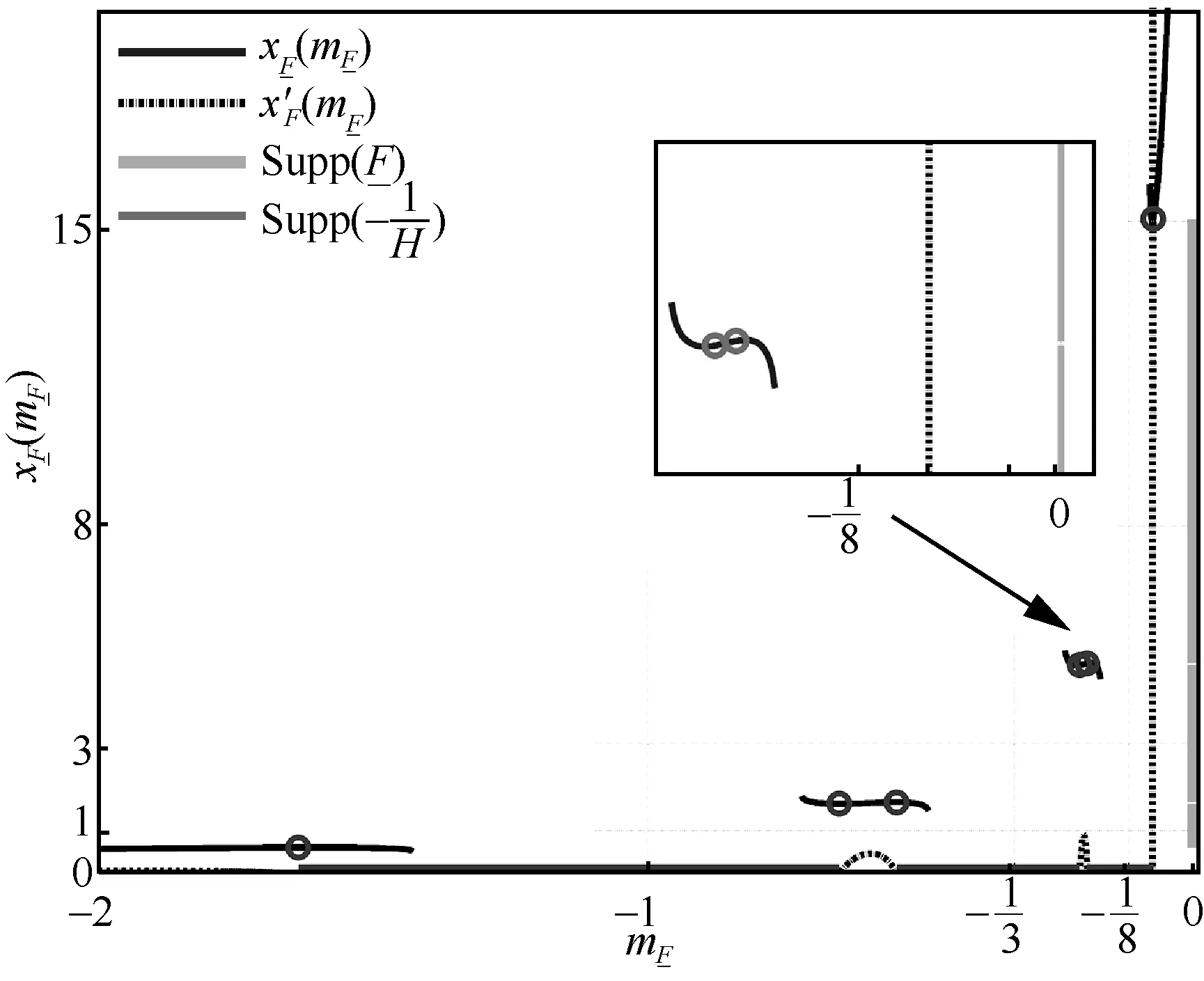
图4 分布支撑集的分离性（f=0.5）

图5 的渐近谱和经验谱分离性（f=0.5）

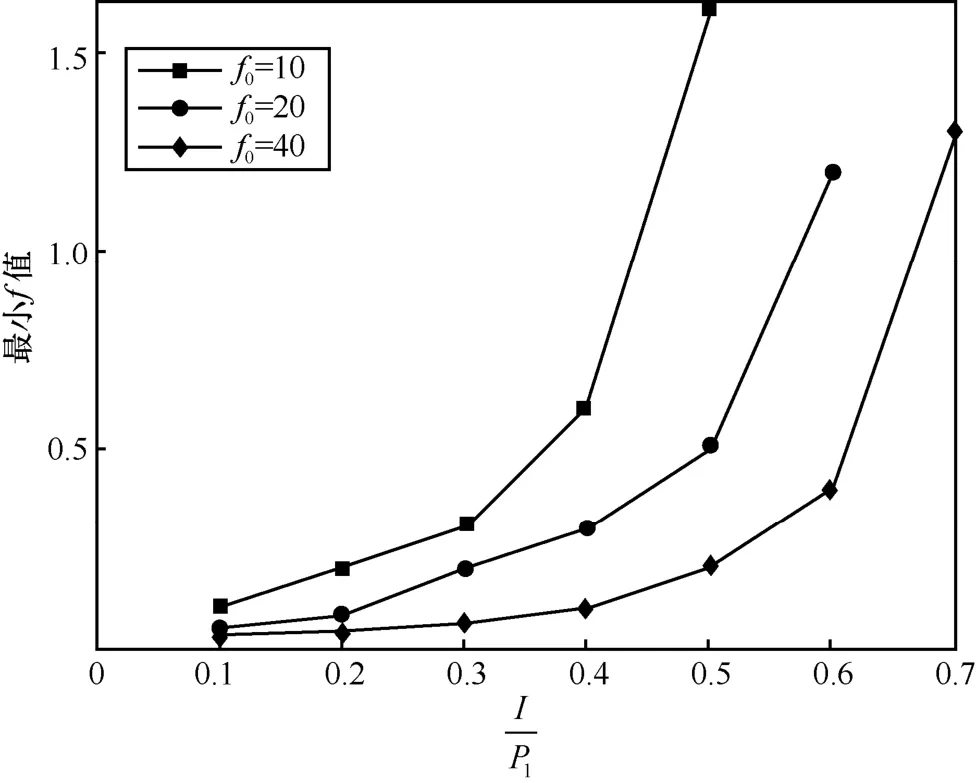
图6 满足可分离条件的最小f值

6 结束语

本文提出了一种适用于massive MIMO 系统的，采用系统参数分层设计，实现了基站接收导频信号的样本协方差矩阵的谱能精确分离，从而消除导频污染的方法，解决了现有的盲导频去污染方法的不足。通过进一步的研究发现期望导频信号与干扰信号之间的功率差异是实现谱分离的重要参数，而非期望导频信号功率越大越好。当已经实现接收信号谱的精确分离后，干扰源的多少并不会影响最终的结果。在此基础上，首次给出了数值方法，当f＜ 1，即所采用的导频序列长度小于基站接收天线数时，仍然能实现谱分离，完全消除了上行信号的导频污染。