波浪滑翔机水下牵引机结构设计与分析

2020-05-10曹守启冯江伟

海洋工程 2020年2期

曹守启，冯江伟

(上海海洋大学工程学院，上海 201306)

近年来，随着世界各国对海洋工程装备不断深入的研究，波浪滑翔机应运而生。作为一种新型海洋工程装备，它克服了传统海洋作业平台需要自带能源的弊端，无需额外提供动力源，仅靠捕获波浪能、太阳能及风能等新能源即可实现行走[1]，具有较高的续航能力和较强的环境适应性，可用于不同海况的海域进行长时间、大范围的监测任务。

目前，关于波浪滑翔机的研究，我国涌现出不少专家学者，并取得了初步成果。李小涛等人将波浪滑翔机与其它监测设备进行了对比[2]，研究发现波浪滑翔机具有长时间、大范围监测的优势。田宝强等人研究了波浪滑翔机的运动效率[3]，论述了水下牵引机的推进原理，分析和计算了波浪的波高和周期对平台运动效率的影响，为后续水下牵引机结构的优化分析提供了理论基础。贾力娟研究了波浪滑翔机的工作机理以及运动情况[4]，建立起波浪滑翔机的二维动力学模型，将模型导入软件进行运动仿真研究。总的来说，我国针对波浪滑翔机的研究仍处于起步阶段，关于该设备的结构设计和三维水动力学分析的相关文献较少。

文中考虑水下牵引机主体结构参数对水动力性能的影响，率先通过ANSYS软件进行三维数值模拟，并采用控制变量法对水下牵引机翼型选择、侧翼板的最大摆动角度及安装分布间距进行水动力仿真研究，将水下牵引机的设计参数作进一步的优化，为同类型波浪滑翔机水下牵引机的设计提供了更加可靠的参考建议。

1 波浪动力滑翔机

1.1 总体结构

波浪滑翔机主要由漂浮在水面上的水面母船和浸没在水中的水下牵引机以及位于二者之间用于连接水面母船和水下牵引机的柔性立管缆绳三大部分组成。水面母船主要用于安装太阳能电池板、风力发电装置、电控系统以及监测系统中用到的各类传感器、水下摄像头和声纳等设备[5]；水下牵引机由垂直安装的主支撑框架和平行安装的侧翼板组成，是整个平台行走的主要动力来源；柔性立管缆绳用于连接水面母船和水下牵引机，并在其内部安装用于水面母船和水下牵引机通信的电缆。图1为波浪滑翔机的三维模型：水面母船长2～3 m，宽0.6～0.8 m；水下牵引机长2～2.6 m，高0.3～0.6 m，侧翼板宽1～1.5 m；柔性缆绳长6～7 m。

1.2 工作原理

波浪滑翔机主要依靠捕获波浪能作为动力源进行推进，同时水面母船上装有太阳能电池板和风力发电装置作为辅助动力源，并通过转向尾舵进行方向的掌控。太阳能电池板和风力发电装置捕获的电能储存在蓄电池中，用于整个平台电力系统的能源供应。在滑翔机随波浪爬升的过程中，柔性缆绳处于紧绷状态，水面母船拖动水下牵引机上移，此时水下牵引机的侧翼板在水动力的作用下向后下方转动，从而产生使水下牵引机向前运动的推力；在滑翔机随波浪回落的过程中，柔性缆绳处于松弛的状态，水下牵引机靠其自身的重力下移，此时水下牵引机的侧翼板在水动力的作用下向后上方转动，从而也产生使水下牵引机向前运动的推力，因此，不论水下牵引机上升还是下移，其侧翼板受到的水平分力总是向前[6]。如此反复，就将滑翔机随波浪的上下起伏运动转化为水下牵引机向前的运动，从而实现了整个波浪滑翔机的持续向前运动。其受力情况如图2所示。

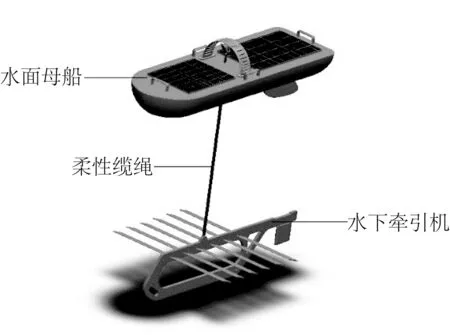
图1 波浪滑翔机三维模型结构示意Fig. 1 Schematic diagram of 3D model structure of wave glider

图2 水下牵引机受力分析Fig. 2 Force analysis of underwater tractor

2 水下牵引机的结构设计

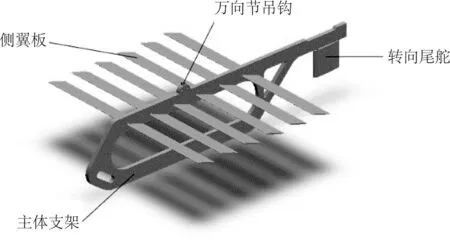
图3 水下牵引机三维模型Fig. 3 3D model of underwater tractor

水下牵引机主要由主体支架、六组互相平行安装的侧翼板、转向尾舵和万向节吊钩等组成，其中，主体支架的结构形状、侧翼板结构的重心和浮心位置会直接影响到整个波浪滑翔机波动推进的效率。因此，水下牵引机在设计过程中需要着重考虑以下几个关键点[7]：①为了保证水下牵引机在升降运动过程中姿态的稳定性，吊点、浮心、重心和水动力中心必须位于同一条竖直线内；②水下牵引机侧翼板的翼型和尺寸需要与实际海况的水流冲刷作用相适应，保证较高的前行效率与适当的垂向往复运动频率；③侧翼板的分布间距和摆动角度应与实际海况相适应，以保证较高的推进效率。

综合目前波浪滑翔机水下牵引机的外形特征，利用Solidworks三维制图软件对水下牵引机进行建模，建模结果如3所示，主要技术参数如表1所示。

表1 水下牵引机设计关键参数Tab. 1 Key parameters of underwater tractor design

3 水下牵引机水动力仿真研究

3.1 理论基础

3.1.1 基本控制方程

在流体仿真计算中，不管是模拟水下牵引机的定常运动，还是模拟水下牵引机的非定常运动，都需要选取恰当的湍流模型。对水下牵引机进行仿真计算时，水流流过其流场，通常状况下将流体看作是不可压缩的液体，并假设在整个计算过程中没有任何热能交换的发生，此时则可以采取不可压缩介质的雷诺平均纳维-斯托克斯(Reynold Saveraged Navier-Stokes, RANS)方程来作为其求解控制方程，流体在流动过程中满足基本的牛顿力学定律、质量守恒定律、动量守恒定律和能量守恒定律[8]，对于黏性的不可压缩牛顿流体建立如下连续方程：

(1)

式中：ui(i=1,2,3)分别为三个坐标轴方向上的速度分量，xi(x=1,2,3)分别为三个坐标轴方向上的坐标分量，P为压力，ρ为流体的密度，v为流体的运动黏性系数，t为时间。

在模拟湍流运动计算时，方程中的变量是由分解平均量和脉动量构成：

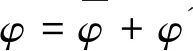
(2)

再对方程左右两侧的时间取平均，得到不可压缩流体RANS方程的张量形式：

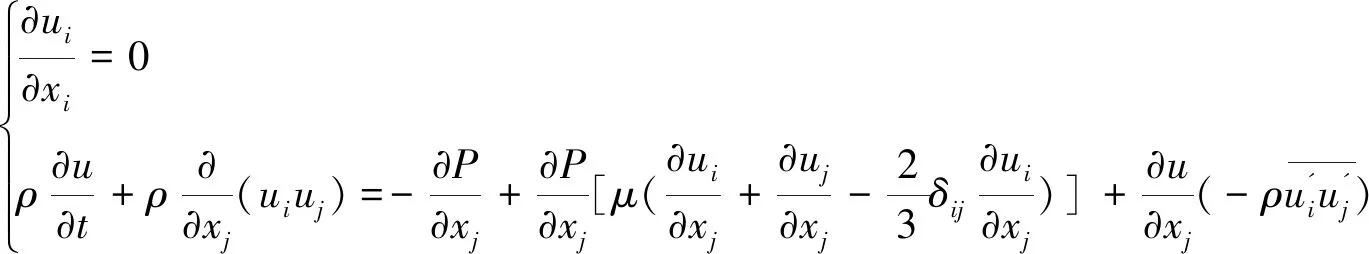
(3)

(4)

式中：k为湍流动能，μt为湍流黏度。

Boussinesq常常用于湍流模型，其优点是在计算湍流黏度时所耗费的时间较少。在k-ε中使用时，必须多解一对方程，分别是与湍流耗散率和湍流动能有关的方程，求解时将μt看成k和ε的函数。Boussinesq黏度有一个很大的缺点：它认为μt是一个标量，在某些情况下使用可能会出现较大的误差。

3.1.2 湍流模型

一般地，模拟湍流时有三种常见的方法：大涡模拟法(LES)、直接数值模拟法(DNS)和平均N-S方程求解法。在模拟湍流方法的计算中，通常采用平均N-S方程的方法进行求解[9]，平均N-S方程求解法用来求解数值模拟中相对较为复杂的一些问题，其本质是对N-S方程中的时间概念进行平均计算，然后得到所建立的湍流时间平均运动方程，即RANS方程。由于平均N-S方程的不封闭性通常含有新的未知数变量——雷诺应力，故湍流模型常用来求解封闭方程组问题。

k-ε湍流模型在计算水下牵引机的流体力学计算中用作广泛。k-ε湍流模型的计算类型共有三种，分别为Standard、RNG和Realizable。通常情况下，RNG计算类型用来求解有涡流存在的一系列较为复杂的问题。本文所设计的水下牵引机体型较小，雷诺数较低，选用RNG计算水动力学参数，计算结果相对准确，也符合实际问题中的理论值。RNG计算如下:

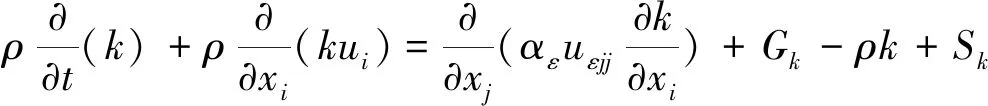
(5)

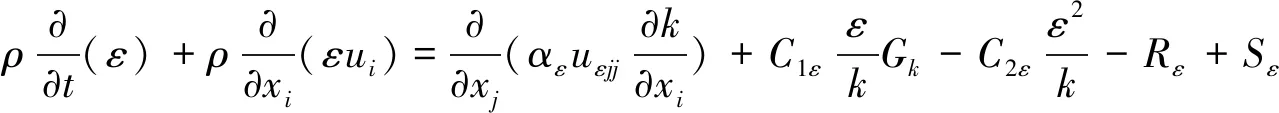
(6)

式中：uεjj为有效黏度，Sk与Sε为源项，Gk为湍流动能，计算如下：

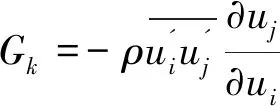
(7)

RNG计算中，湍流黏度方程为：

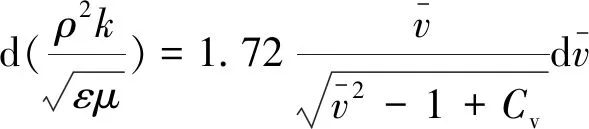
(8)

当雷诺数变高时，方程变形如下：

(9)

式中：Cμ和Cv为经验系数。

3.2 仿真分析

3.2.1 计算域设置和网格划分

水下牵引机的三维模型建立好后，需要根据模型的尺寸设置计算域进而进行网格的划分，设置计算域时一定要保证二者在尺寸上的适应性。采用长方体的计算域，在平行于水流流向的方向，取6倍于水下牵引机的高度为尺寸，在垂直于水流流向的方向，分别取3倍于水下牵引机的长度和宽度为尺寸建立计算域，这样可以基本保证计算的合理性。网格的划分不仅直接影响计算结果的精度，而且对计算时间的长短也影响较大，因此在划分网格时要进行综合考虑，在满足计算精度的前提下，尽量将计算时间控制到最短。在进行网格划分时，整体采用非结构网格划分，并进行局部加密处理[10]，最终的网格单元总数约为2 066 558，其中全局网格大小为3 mm，面网格大小为20 mm，part网格大小为5 mm，fluid网格大小为10 mm，符合计算的基本要求。网格划分结果如图4所示。

图4 计算域和水下牵引机网格划分结果Fig. 4 Meshing results of calculation domain and underwater tractor

3.2.2 边界条件设定

水下牵引机在竖直方向的运动状态为随波浪的起伏运动，文中所有模型的水动力分析均选取柔性缆绳拉动水下牵引机向上运动的过程，水流方向相对于水下牵引机的方向为竖直向下。将长方体流域的上边界设置为速度入口(velocity-inlet)，下边界设置为压力出口(pressure-outlet)，四周边界设置为远边界(wall)。根据实际对海洋状况的研究，并结合海况等级表取平均海况为3级海况，则海面以下6～7 m处海水的垂直流速为0.75 m/s左右，因此仿真计算时取入口处的速度为0.75 m/s，迭代计算的步数设为1 000，以保证模型计算的收敛性。

此外，取海洋环境条件为：海水温度4°C，海水密度1 027.77 kg/m3，海水运动黏性系数1.6110-6m2/s。

3.2.3 计算模型

波浪滑翔机的主要动力来源于水下牵引机水翼的摆动，六组平行翼板翼型的选择、翼板的最大摆动角度以及翼板的安装间距均对波浪滑翔机的行走效率有着较大影响。因此，经过将模型简化，建立了如下三组对比计算模型：1)在其它因素均相同的条件下分别取NACA0012翼型和平板翼型进行对比仿真；2)在其它因素均相同的条件下分别取水翼的最大摆动角度θ为：5°、10°、15°、20°、25°、30°进行对比仿真；3)在其它因素均相同的条件下分别取水翼的安装间距d为：40、80、120、160、200和240 mm进行对比仿真。

3.3 仿真结果及分析

3.3.1 翼型的选择

图5、图6、图7为相同参数设置下NACA翼型和平板翼型的压力云图、流场流线图以及速度矢量图。

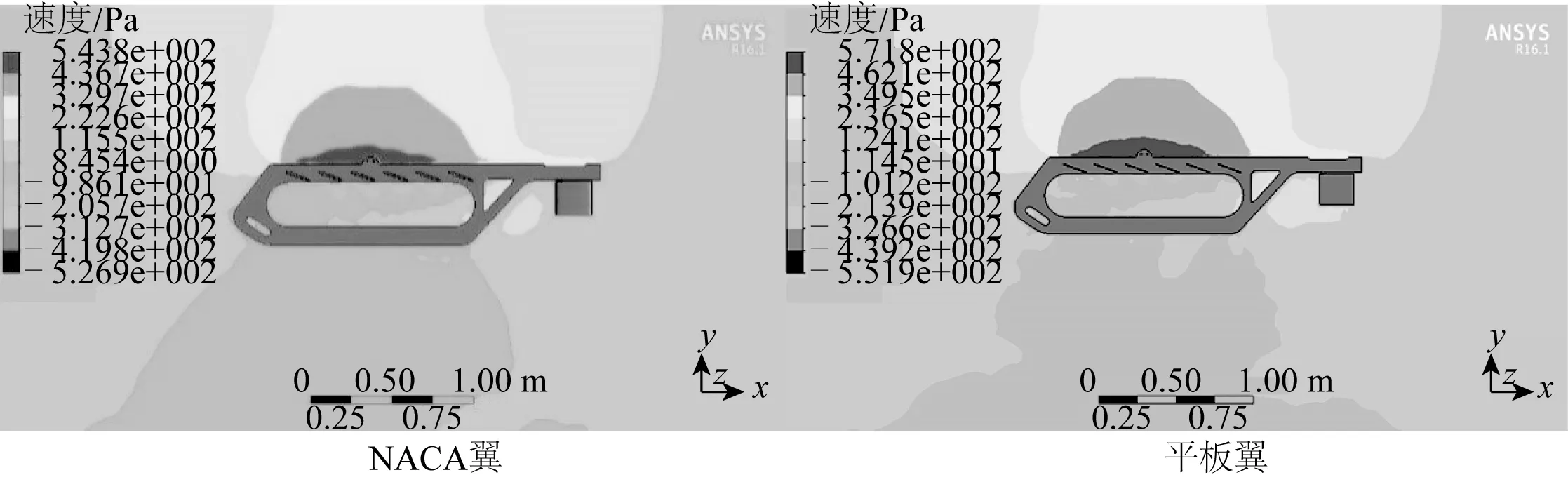
图5 NACA翼型和平板翼型压力云Fig. 5 Pressure cloud diagram of NACA airfoil and flat airfoil

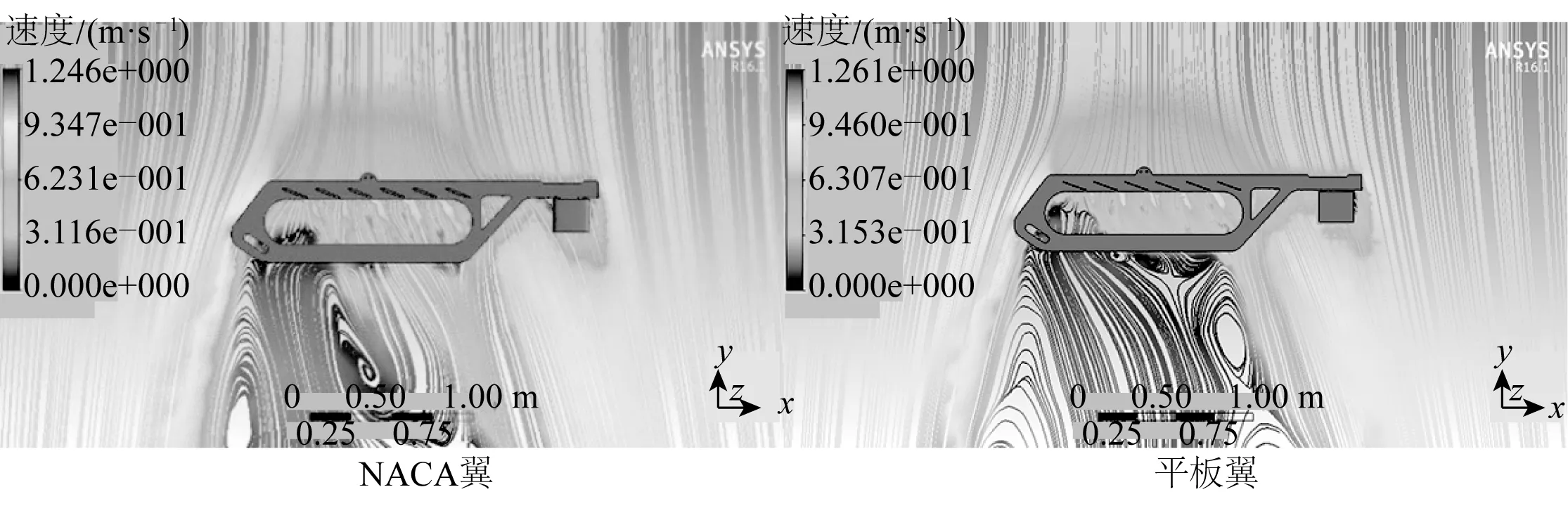
图6 NACA翼型和平板翼型流场流线Fig. 6 Flow field curves of NACA airfoil and plate airfoil

图7 NACA翼型和平板翼型速度矢量Fig. 7 Velocity vector of NACA airfoil and flat airfoil

由分析结果可知，在相同参数的情况下，NACA翼型的升阻比更大，即在同等海况的条件下，NACA翼型可获得更大的前向推力。此外，平板翼型的侧翼板所受压力区域较为集中，在承受较大的压力时，容易引起侧翼板的屈曲，以至于影响水下牵引机的整体推进效率，甚至可能引发水下牵引机的失效；而NACA形水翼所受的压力区域则较为分散，同时还有结构强度高，阻力系数小，水动力性能好等优点。尽管NACA翼板的加工成本远高于平板水翼，但综合各方面因素，将水下牵引机侧翼板的形状选为NACA0012型侧翼板。

3.3.2 最大摆角确定

图8为NACA0012型侧翼板在相同来流速度、相同分布间距、相同运动波长等因素下，只控制最大摆动角度不同时所得到的压力云图，最大摆动角度θ的取值为：5°、10°、15°、20°、25°、30°。其中，水下牵引机在不同最大摆动角度下的仿真计算结果如表2所示。

表2中各项计算流体力学(CFD)参数为通过仿真计算得到的不同最大摆动角度下水下牵引机所受的总阻力、前向推力、总阻力系数、推力系数以及进一步计算求出的升阻比。为了更加直观地显示总阻力和推力的变化趋势，将表2数据绘制为图9、图10所示的曲线图。

图8 不同最大摆角时压力云图Fig. 8 Pressure cloud diagram at different maximum yaw angles

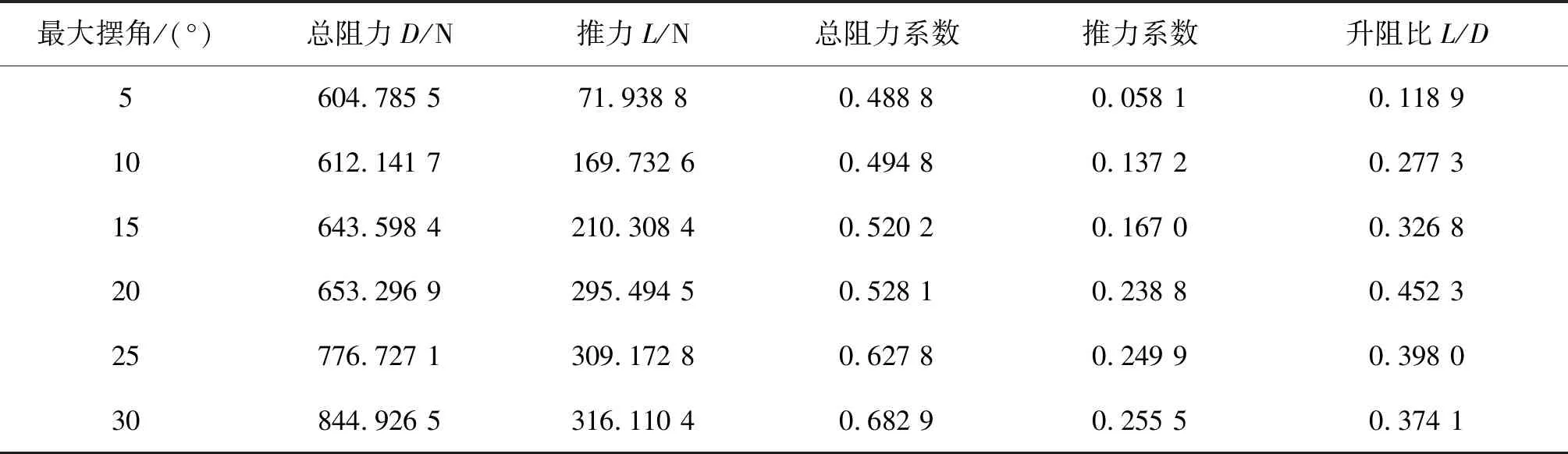
表2 不同水翼最大摆角—CFD分析结果Tab. 2 Maximum swing angle of different hydrofoils—CFD analysis results

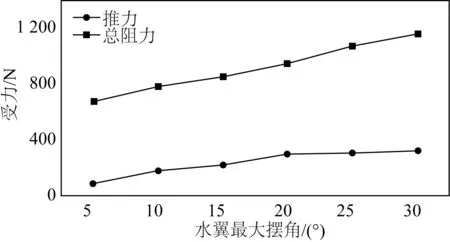
图9 不同最大摆角受力曲线Fig. 9 Force curves with different maximum yaw angles

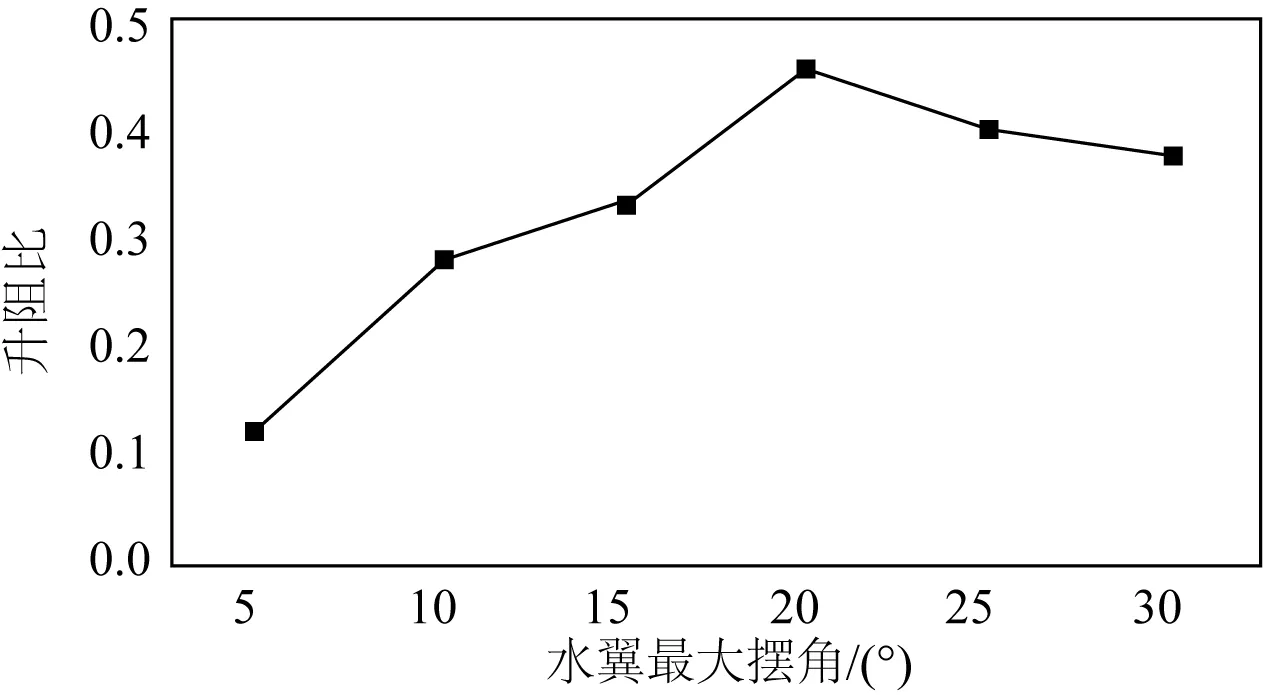
图10 不同最大摆角升阻比Fig. 10 Lift-drag ratios at different maximum yaw angles

分析以上图表可知，在来流速度、侧翼板分布间距、运动波长等因素一定的条件下，每个水翼所受的推力系数随最大摆动角度的变化规律大致相同，均为先增大后减小，由此可见，侧翼板的最大摆动角度存在一个最佳的数值。随着最大摆动角度的增大，推力L和阻力D均增大，只是在最佳数值之前，推力L增加的幅度大于阻力D增加的幅度；而在最佳数值之后，阻力D增加的幅度则大于推力L增加的幅度，所以升阻比表现为先增大后减小。从仿真计算的结果来看，这一最佳数值位于θ=20°附近。

3.3.3 最佳安装间距选取

图11为NACA0012翼型在最大摆动角度θ=20°，且设置来流速度、运动波长等因素均相同时，侧翼板在不同水翼分布间距下所得到的压力云图。安装间距d的取值为：40、80、120、160、200和240 mm。其中，水下牵引机在不同安装间距下的仿真计算结果如表3所示。

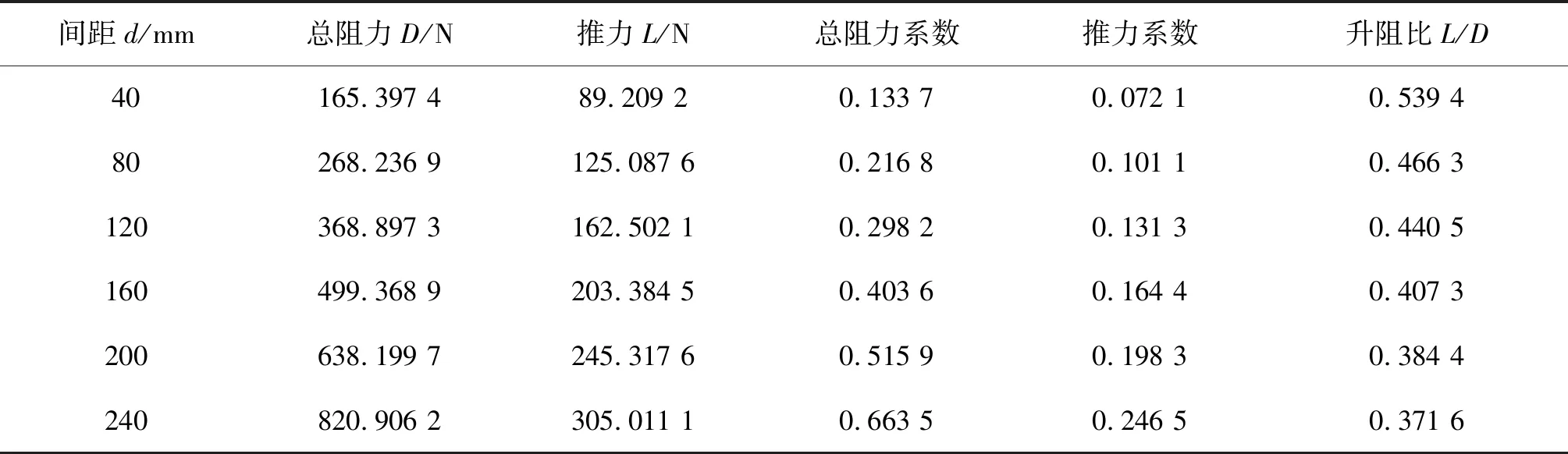
表3 不同水翼分布间距—CFD分析结果Tab. 3 Different hydrofoil spacing—CFD analysis results

表3中的各项CFD参数为通过仿真计算得到的侧翼板在不同分布间距下水下牵引机所受的总阻力、前向推力、总阻力系数、推力系数以及进一步计算求出的升阻比。为了更加直观地显示总阻力和推力的变化趋势，将表3绘制为如图12、图13所示的曲线图。

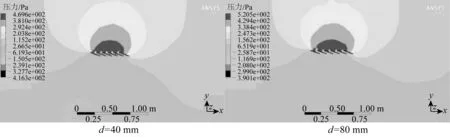
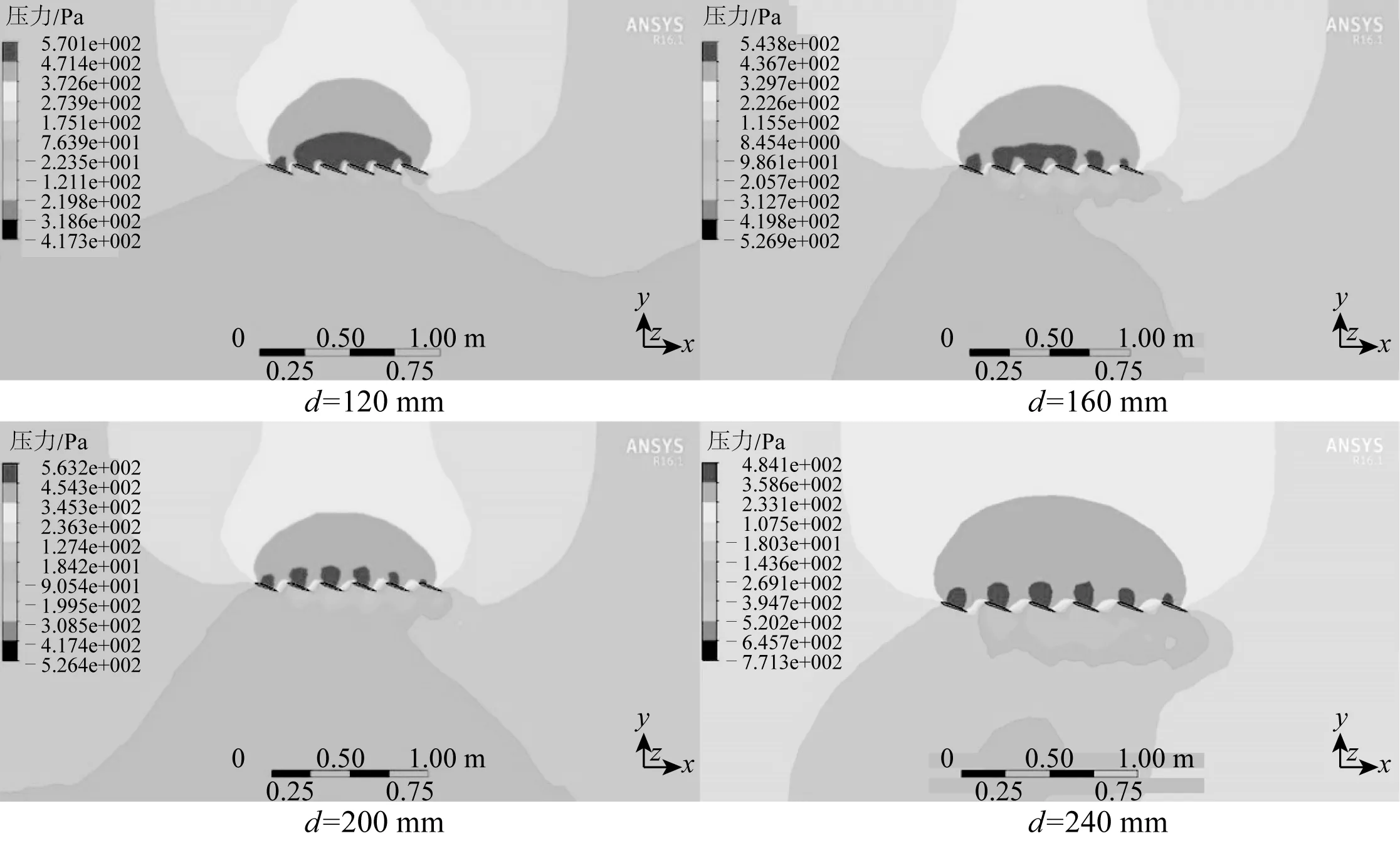
图11 不同分布间距时压力云图Fig. 11 Pressure cloud diagram at different spacing distributions

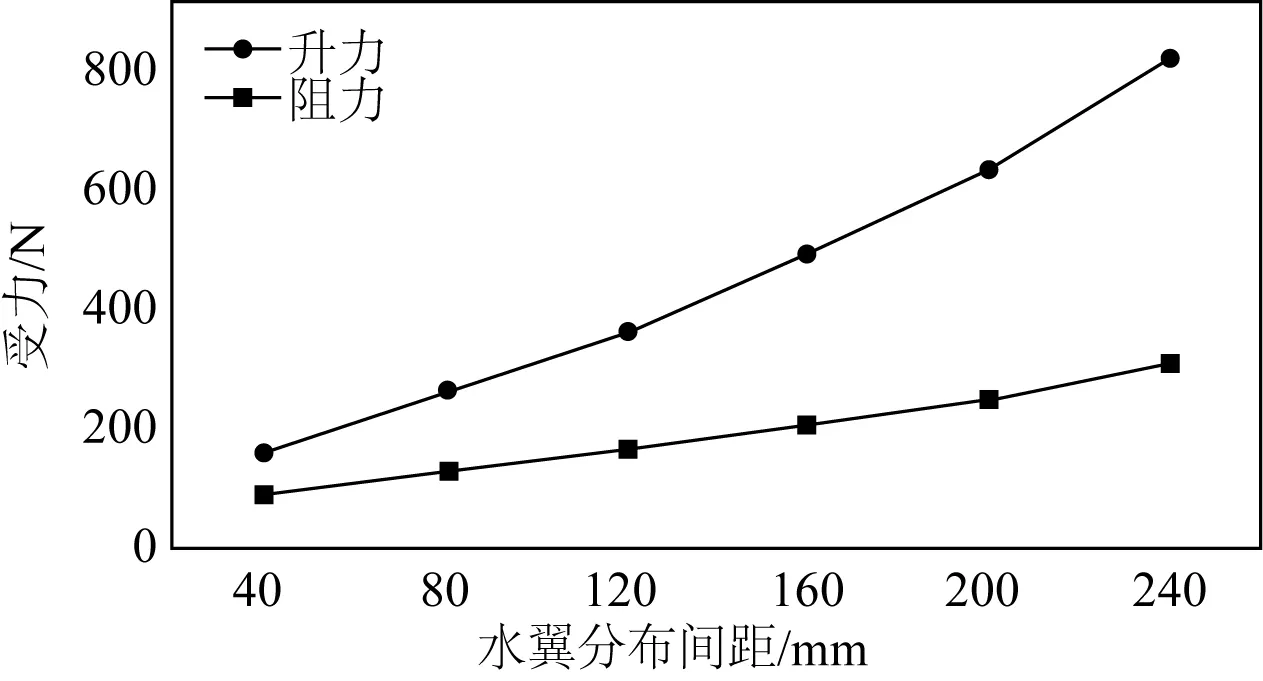
图12 不同水翼分布间距受力曲线Fig. 12 Stress curves of different hydrofoil spacing

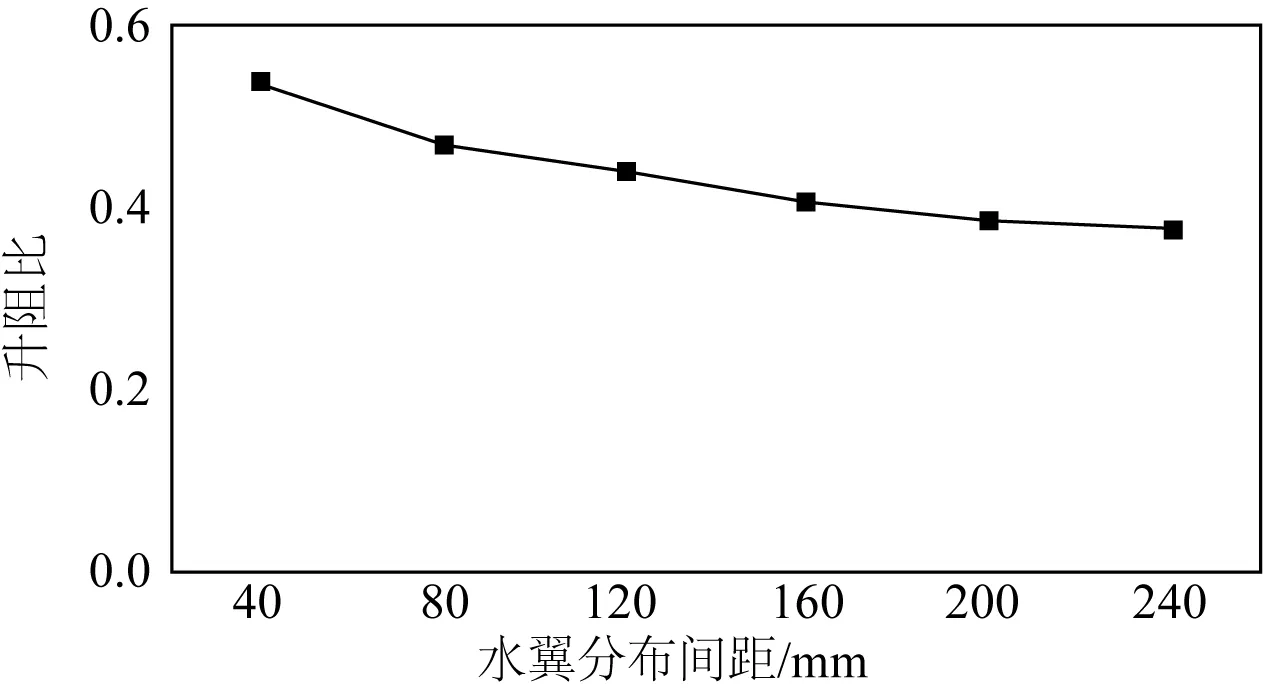
图13 不同水翼分布间距升阻比Fig. 13 Lift-drag ratios of different hydrofoil spacing

分析以上图表可知，在来流速度、侧翼板最大摆动角度、运动波长等因素一定的条件下，每个水翼所受的推力系数随分部间距的变化规律大致相同，都是随分部间距的增大而减小。由此可见，适当减小水翼分部间距对提高水下牵引机的总体推进效率是有益的，因为在不同水翼分布间距下每个水翼产生的首缘涡和尾涡的方向基本相同，但强度各异，随水翼分布间距的增大，首缘涡和尾涡的强度均有所衰减。水翼分布间距较小时，前面水翼的尾涡还未完全衰减，就与后面水翼的首缘涡融合在一起，如此传递，使得每个水翼的尾涡均有一定程度的加强，从而产生较强的前向推力；而当水翼分布间距较大时，每个水翼所产生的首缘涡和尾涡衰减程度都较大，各旋涡之间的相互影响较小，产生的前向推力也较弱。当间距过小时，虽然其侧翼板获取的推力最大，但压力负载区域过于集中，水下牵引机的稳定性较差，从而影响其总体推进效率，综合考虑，取水翼分部间距为d=80 mm时总体推进效果最佳。