海洋工程中双柔性圆柱流激振动响应特性

徐万海，李宇寒，闫术明，马烨璇

(1. 天津大学 水利工程仿真与安全国家重点实验室，天津 300072; 2. 中国石油天然气管道工程有限公司，河北 廊坊 065000)

海洋立管、海底管线和浮式平台系泊缆等柔性圆柱结构长径比大、阻尼比低、质量比小，极易在海流的作用下发生流激振动(flow-induced vibration，简称FIV)。流激振动是造成上述结构疲劳损伤的重要因素。关于单个柔性圆柱结构的流激振动研究已有很多，并取得了大量研究成果[1-5]。但实际工程中，圆柱结构并不总是单独存在，通常会与周围的结构组成多圆柱系统，多圆柱的尾流发生相互干涉，使多圆柱系统的流激振动特性更为复杂[6-8]。

双圆柱系统通常被看作多圆柱系统的基本组成单元，为了研究多圆柱系统的流激振动特性，一些学者研究了双刚性圆柱的流激振动[9-10]。对于并列的弹性支撑刚性圆柱，间距比(圆柱中心间距与外径的比值)小于1.5时，两圆柱的相互作用会抑制结构的振动；间距比为1.7时，高流速下两圆柱的响应位移大于单圆柱的结果[11]；间距比为4.0时，并列双刚性圆柱之间的相互影响基本可被忽略[12]。串列弹性支撑刚性圆柱的流激振动特性更为复杂。Assi等[13]试验研究了弹性支撑刚性圆柱在固定圆柱尾流影响下的单自由度振动特性，下游圆柱的横流向位移在“锁频”区后显著增大。上游固定圆柱的尾流对下游圆柱的影响随间距比增大而减弱。随后，Assi等[14]进一步研究了弹性支撑刚性圆柱在固定圆柱尾流影响下的双自由度振动特性，结果表明下游圆柱的双自由振动响应与单自由度响应相比并无本质上的差异。当上游圆柱也能振动时，间距比大于4.0的情况下，下游圆柱对上游圆柱的影响较小，上游圆柱的振动特性与单圆柱相似。但受上游圆柱尾流的影响，下游圆柱的响应位移会显著增大[15]。弹性支撑刚性圆柱交错排布时，上游圆柱和下游圆柱的响应模式随圆柱横流向和顺流向之间的间距比发生变化，结构可能会发生涡激振动也可能会发生驰振[16]。下游圆柱的运动轨迹与上游圆柱的结果相比存在显著差异[17]。柔性圆柱具有多阶固有频率，流激振动响应通常表现为多模态特性。因此，双柔性圆柱系统的流激振动特性与双刚性圆柱系统相比更为复杂。Huera-Huarte和Gharib[18]试验研究了并列双柔性圆柱的流激振动特性，结果表明：间距比大于等于3.5时，两圆柱之间的同步振动减弱。而Sanaati和Kato[19]的试验结果表明，并列双柔性圆柱的间距比为5.5时，两圆柱的振动仍存在显著的相互影响。Huera-Huarte和Gharib[20]试验研究了串列柔性圆柱的流激振动特性，两圆柱的间距比为4.5～8.0。随着间距比的增大，上游圆柱的响应与单圆柱的响应呈现明显的相似性。下游圆柱在“锁频”区表现为经典的涡激振动，而在“锁频”区后表现为尾流诱发振动(wake-induced vibration，简称WIV)。Prastianto等[21]开展了交错布置的双柔性圆柱流激振动试验，结果表明：随着两圆柱横流向间距比的增大，圆柱之间的相互作用逐渐减弱；横流向间距比较大时，两柔性圆柱的运动轨迹与单圆柱相似。

目前，关于柔性圆柱结构多柱体的流激振动特性研究仍然较少，许多现象和机理仍尚未明确。为了弥补相关研究的不足，基于双柔性圆柱流激振动试验，采用模态分析法将测量得到的应变信息转化为位移，分析了双柔性圆柱在并列、串列和交错排布方式下的流激振动特性。相关研究成果可为海洋工程中多根柔性圆柱系统的设计提供一定的参考和借鉴。

1 模型试验

柔性圆柱结构多柱体的流激振动试验在拖曳水池中开展，水池尺寸为137.0 m×7.0 m×3.3 m(长×宽×深)。柔性圆柱模型#1和#2具有相同的物理参数，如表1所示。柔性圆柱模型由内部铜管和外部硅胶管构成，铜管外径8 mm，壁厚1 mm，其外表面黏贴应变片，外部包裹硅胶管，整个模型的外径为16 mm，模型均布7个测点(G1～G7)，整体布置如图1所示。至于测点布置的数量，文中分析的模型在横流向和顺流向下分别所能达到的最高模态为4阶和6阶，借鉴相关学者在模态法重构位移方面的已有成果以及模态法的相关原理，设置7个测点能确保识别出结构振动的6阶模态，可满足测量的需求。电阻应变片黏贴于铜管各测点处，分别测量结构横流向和顺流向的应变。外部硅胶管既能提供光滑规则的外表面，又能保护应变片和测量导线。如图2所示，圆柱模型通过万向节固定于试验装置一侧的支撑板上，另一侧通过钢丝绳依次连接弹簧、张紧器和拉力传感器。试验过程中，横向支持架与拖曳水池上的拖车相连，试验装置的导流板完全浸没于水中，圆柱模型距水面约1.0 m。通过拖车匀速前进模拟均匀来流，来流速度为0.05～1.00 m/s，速度间隔为0.05 m/s。每个流速工况的采样时间为50 s，采集频率为100 Hz。试验中两圆柱的相对位置如图3所示，包括并列、串列和交错位置共21组工况。S表示两圆柱横流向的中心间距，T表示两圆柱顺流向的中心间距。

表1 柔性圆柱模型参数Tab. 1 The parameters of the flexible cylinder model

图1 试验圆柱横切面布置及应变片轴向位置示意Fig. 1 A sketch of cross section of experimental cylinder and layout of strain gauges along the axis

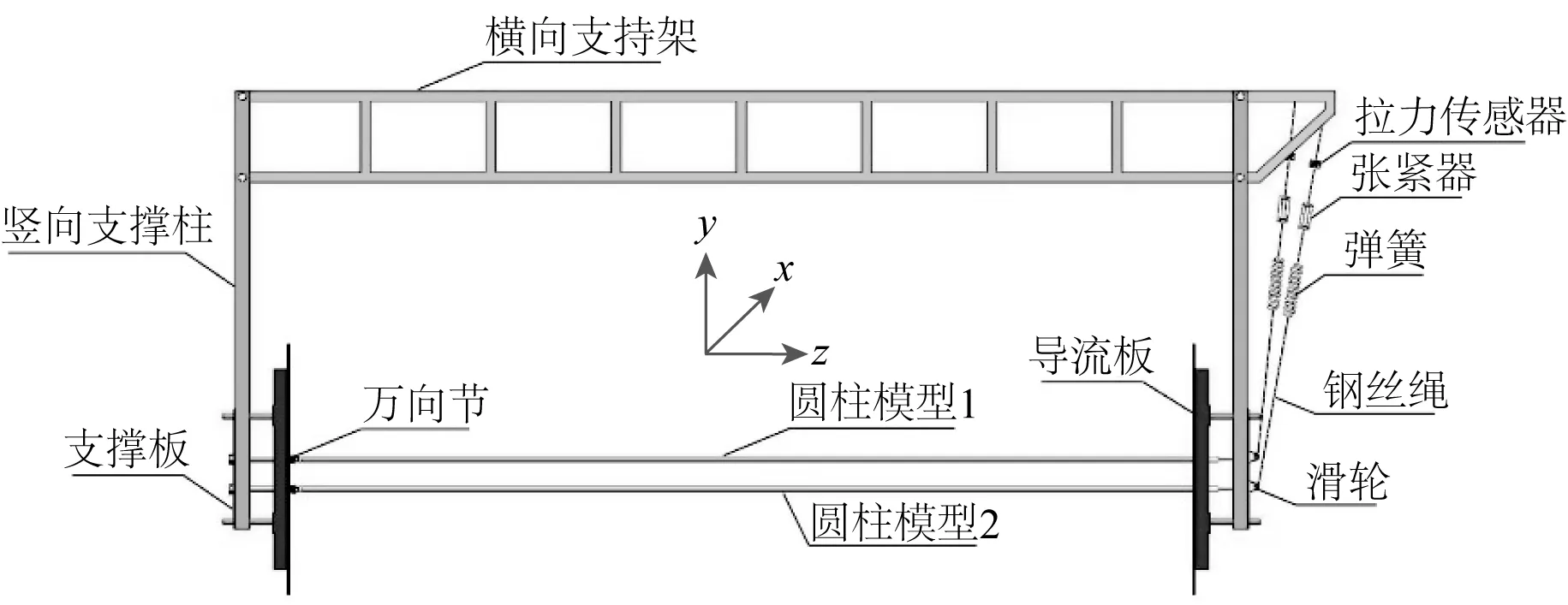
图2 试验装置示意Fig. 2 Schematic diagram of the experimental setup

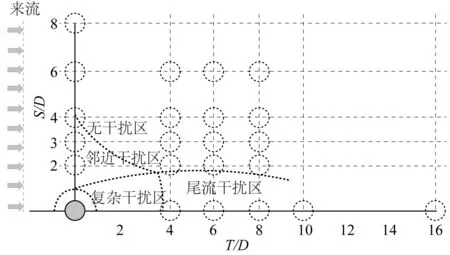
图3 试验中两圆柱模型相对位置示意Fig. 3 Relative position of two cylinder models in the test

2 数据处理

试验中直接测量的是柔性圆柱模型的应变信息，采用模态分解法即可将试验测量的应变信息转化为柔性圆柱位移[1-2, 22]。为简化起见，仅以横流向位移的重构为例进行说明。圆柱结构位移可写为：

(1)

式中：y(z,t)为横流向的位移，z为轴向坐标，t为时间，wn(t)为模态权重，n为圆柱结构的模态阶次，M为确定结构位移所需的模态数目，φn(z)为模态函数。试验中圆柱为两端简支约束，φn(z)可表示为：

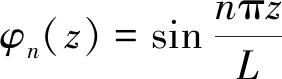
(2)

根据应变与位移的关系可得：

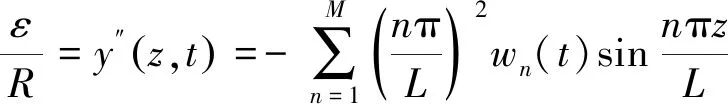
(3)

式中：ε为测量获得的应变，R为铜管半径。由式(3)可以求得模态权重，将模态权重代入式(1)即可获得结构位移。顺流向位移的重构方法与横流向类似，但在计算顺流向位移时，需先去除顺流向平均挠曲变形产生的应变，仅重构顺流向的振动位移。

3 结果分析

单圆柱在均匀流作用下，当涡脱频率接近结构某阶固有频率时，“锁定”现象发生，该阶模态即为结构振动的主控模态，其模态权重最高，其它阶次模态的权重相对较小。计算不同约化速度下结构振动的各阶模态权重，若某阶模态的权重占绝对主导地位，则表明在该约化速度下结构发生该阶模态的“锁定”，也称振动的主控模态为该阶，即该约化速度位于“锁频”区[1]。

随着约化速度的增大，可能发生下一阶模态的“锁定”，称这个主控模态升阶的现象为“模态转化”，在下一阶模态“锁定”发生前的约化速度区间定义为“模态转化区”。在模态转化区，存在模态竞争现象，相邻两阶模态的权重在大小上相当。可以通过计算各阶模态的模态权重，大致判断某个特定的约化速度位于锁频区，还是模态转化区。

为了方便比较单圆柱与双圆柱的结果，下文中所提及的“锁频区”和“模态转化区”均是针对单圆柱的FIV。

3.1 并列柔性圆柱的FIV响应

图4为并列柔性圆柱横流向最大位移均方根与单圆柱结果的比值。

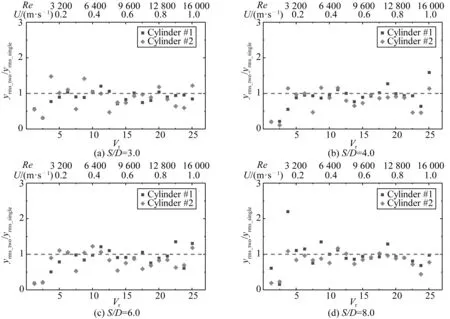
图4 并列柔性圆柱横流向最大响应位移均方根与单圆柱结果比值Fig. 4 Max RMS displacement ratio of side-by-side cylinders to single cylinder versus reduced velocity in the CF direction

横流向最大位移均方根为结构轴向所有节点位移均方根的最大值，其计算公式为：

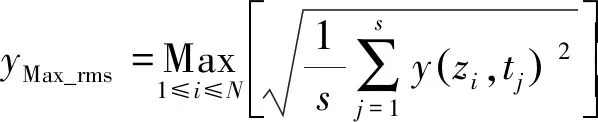
(4)

式中：s代表节点个数。顺流向最大位移均方根的计算方法类似，但需要在计算前去除均匀来流作用下产生的平均位移。

当约化速度(Vr=U/f1D)小于3.76时，柔性圆柱#1和#2的最大位移均方根均小于单圆柱的结果。约化速度大于5.01且间距比S/D=3.0, 4.0和6.0时，柔性圆柱#1和#2的最大位移均方根与单圆柱的结果呈现较大的差异。而在间距比S/D=8.0时，柔性圆柱模型#1和#2的最大位移均方根与单圆柱的结果较为接近。上述现象表明，并列柔性圆柱之间的间距比为6.0时，两圆柱横流向的振动仍存在较为强烈的干扰，间距比为8.0时横流向振动之间的相互干扰减弱。Sanaati和Kato[19]通过试验研究表明间距比为5.5时并列柔性圆柱之间的振动存在强烈的相互影响，与本文的结果一致。

图5为并列柔性圆柱顺流向最大位移均方根与单圆柱结果的比值。柔性圆柱#1和#2的最大位移均方根在绝大多数约化速度下大于单圆柱的结果，尤其是圆柱振动发生模态转化时，例如约化速度为6.26～7.52，13.78～15.03和22.55～23.80，其对应的控制模态分别由2阶向3阶、3阶向4阶、5阶向6阶转化。由于圆柱之间的相互影响，并列柔性圆柱顺流向的位移显著增大。间距比为8.0时，并列柔性圆柱顺流向的振动仍存在较强的相互影响。Sanaati和Kato[19]试验测量了并列柔性圆柱顺流向的脉动流体力，结果表明：约化速度大于6.74后，并列柔性圆柱顺流向的脉动流体力系数大于单圆柱的结果。虽然圆柱顺流向的流体力系数在本文试验中并未直接测量，但根据Sanaati和 Kato[19]的结果可知，并列柔性圆柱顺流向位移的增大与顺流向脉动流体力系数的增大有关。

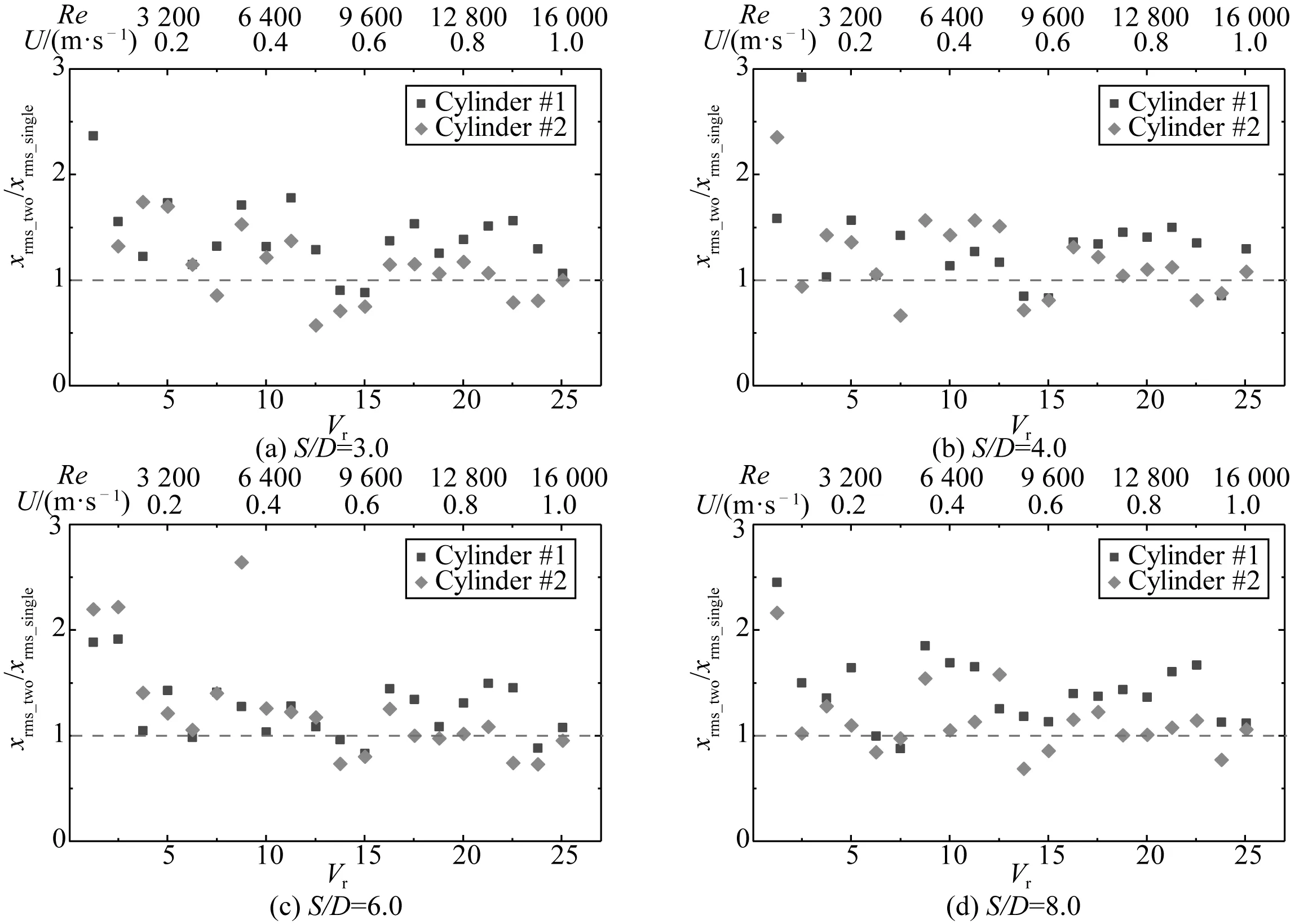
图5 并列柔性圆柱顺流向最大响应位移均方根与单圆柱结果比值Fig. 5 Max RMS displacement ratio of side-by-side cylinders to single cylinder versus reduced velocity in the IL direction

3.2 串列柔性圆柱的FIV响应

图6为柔性圆柱串列布置时上游圆柱最大位移均方根与下游圆柱结果的比值。上游圆柱横流向的响应位移大多位于下游圆柱位移的0.5～1.5倍之间，而上游圆柱顺流向的位移大多位于下游圆柱位移的0.5～2.5倍之间。两圆柱顺流向位移比的分布更为散乱，表明两圆柱之间的间距比对顺流向位移的影响更为显著。大多数约化速度工况下，上游圆柱横流向和顺流向的位移大于下游圆柱的结果。主要原因在于上游圆柱对下游圆柱存在遮蔽效应，下游圆柱的局部流速小于均匀来流速度。间距比为16.0时，上游圆柱对下游圆柱仍存在较强的遮蔽效应。Assi等[13]关于单自由度串列刚性圆柱流激振动的研究结果表明，下游圆柱受上游圆柱尾迹的影响振动幅值显著增大，出现WIV现象。但本文的结果表明，对于串列柔性圆柱而言，仅在某些约化速度下，下游圆柱的位移略高于上游圆柱的结果，但并未出现显著的增大。出现上述差异的原因是：刚性圆柱的振动为单模态，WIV通常发生于“锁频”区之后；而柔性圆柱具有多阶固有频率，某一阶模态的“锁频”区结束后，会激发下一阶模态，因此未出现显著的WIV现象。

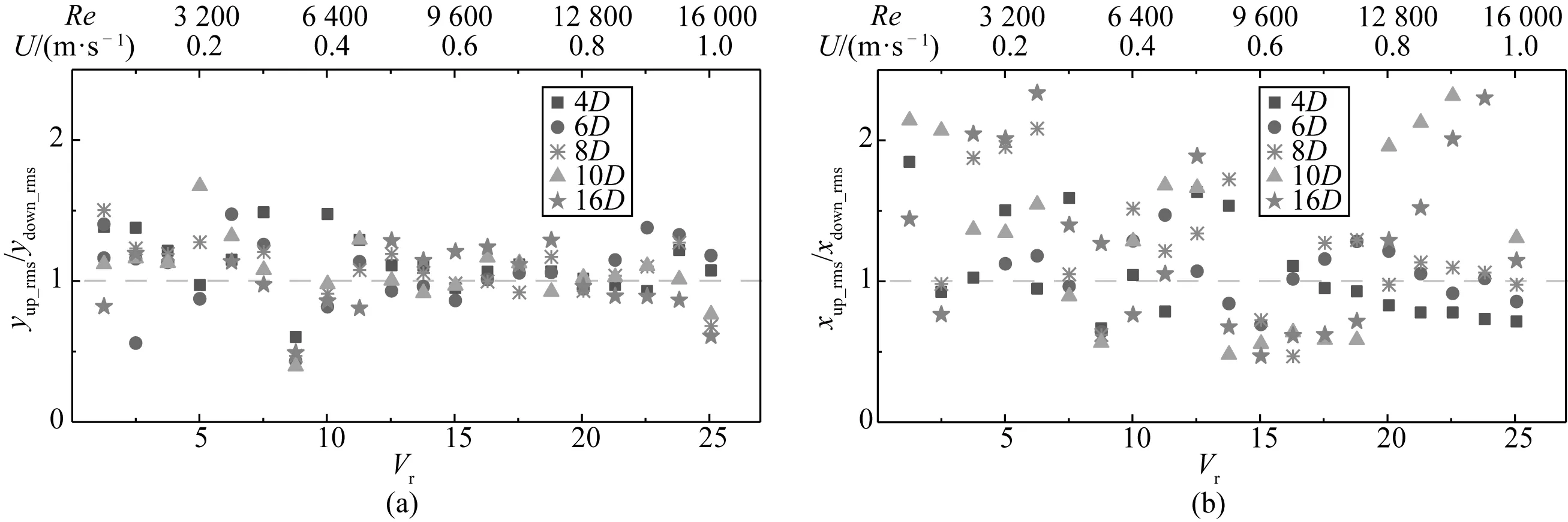
图6 串列布置时上游圆柱最大位移均方根与下游圆柱结果比值Fig. 6 Max RMS displacement ratio of the upstream cylinder to the downstream one versus reduced velocity in a tandem arrangement

图7和图8为串列柔性圆柱与单圆柱横流向和顺流向的位移云图，选取的工况为T/D=10.0,Vr=10.03。在此工况下，单圆柱横流向振动的控制模态为2阶，顺流向振动的控制模态为3阶。横流向和顺流向的位移沿圆柱轴向呈非对称式分布。与单圆柱的结果相同，上游圆柱横流向和顺流向的控制模态分别为2阶和3阶。表明下游圆柱对上游圆柱的响应特性影响较小。但上游圆柱对下游圆柱的响应位移影响显著，下游圆柱横流向和顺流向的控制模态均为1阶。由于上游圆柱对下游圆柱存在遮蔽效应，下游圆柱的局部流速小于自由来流速度，所以下游圆柱的振动控制模态低于上游圆柱和单圆柱的结果。

图7 串列柔性圆柱与单圆柱横流向位移云图(T/D =10.0, Vr=10.03)Fig. 7 Space-time varying dimensionless CF displacement contours of the tandem cylinders and the single one with T/D = 10.0, Vr=10.03

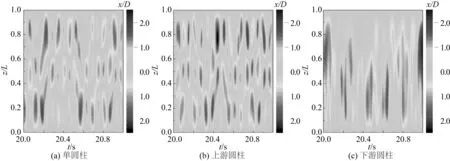
图8 串列柔性圆柱与单圆柱顺流向位移云图(T/D =10.0, Vr=10.03)Fig. 8 Space-time varying dimensionless IL displacement contours of the tandem cylinders and the single one with T/D=10.0, Vr=10.03

3.3 交错柔性圆柱的FIV响应

由于柔性圆柱交错排布时开展的试验工况较多，仅展示部分典型结果。分析所有交错工况的结果后发现：上游圆柱受下游圆柱的影响较小，而下游圆柱受上游圆柱的影响较大。以T=8D时，下游圆柱的响应结果为例进行分析。图9和图10分别绘出了下游柔性圆柱和单圆柱横流向和顺流向的最大位移均方根。图9和图10中的虚线表示单圆柱的结果。

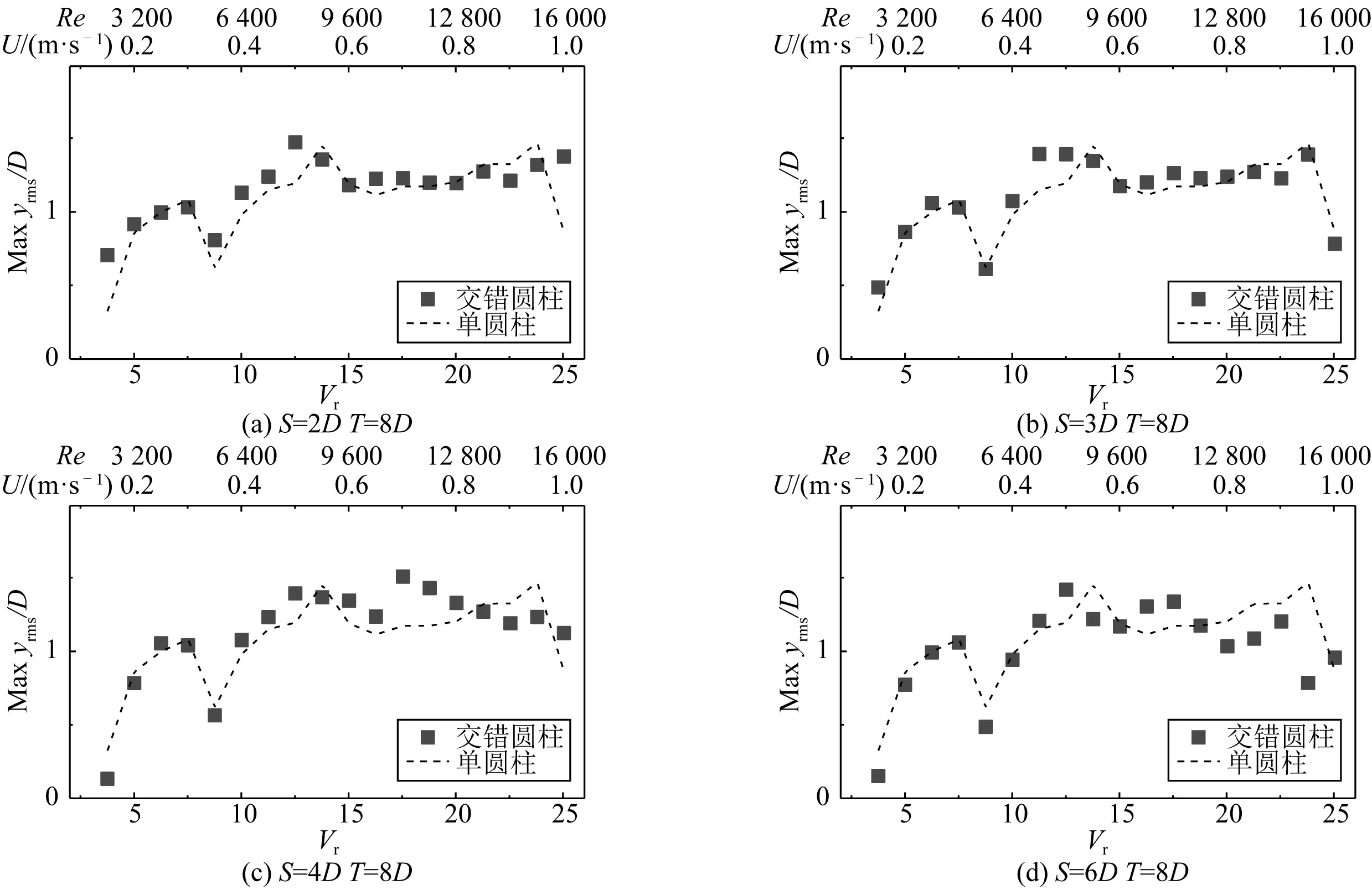
图9 交错布置时下游柔性圆柱与单圆柱横流向最大位移均方根Fig. 9 Max CF RMS displacement of the downstream cylinder and the single one in a staggered arrangement

图10 交错布置时下游柔性圆柱与单圆柱顺流向最大位移均方根Fig. 10 Max IL RMS displacement of the downstream cylinder and the single one in a staggered arrangement

可以发现，下游圆柱横流向最大位移均方根与单圆柱的结果吻合较好，仅在某些约化速度下存在较小的差异。但下游圆柱的顺流向最大位移均方根与单圆柱的结果存在显著差异。根据模态权重及对应的控制频率，顺流向振动的各个“锁频”区对应的约化速度范围为：一阶锁频区1.25～2.51、二阶锁频区5.01～6.26、三阶锁频区10.02～12.52、四阶锁频区15.03～16.28、五阶锁频区20.04～21.29、六阶锁频区23.80～25.05。在“锁频”区的后半段，下游圆柱的顺流向位移并未像单圆柱的位移那样减小，而是持续增大。

为了分析下游圆柱顺流向位移增大的原因，绘制了S=6D，T=8D，Vr=7.52时下游圆柱中点处横流向、顺流向位移的时频图和运动轨迹，如图11所示。图11中的小波系数是位移信号经过小波分解后得到的小波基函数的线性系数，反映了小波基函数与原信号的相关程度。小波系数可以理解为各个频率成分的权重系数，每一频率对应一个小波系数，小波系数越大，则代表信号频率与该频率的相关性越高，集中在该频率上的能量也就越大。不难看出，下游圆柱横流向和顺流向的控制频率相同，均为2.90 Hz，对应的运动轨迹为椭圆形。已有研究表明，单圆柱顺流向的控制频率为横流向控制频率的2倍，运动轨迹为“8字”形。产生上述差异的原因是：下游圆柱受上游圆柱尾流的影响发生了“Wake-flutter”。“Wake-flutter”现象的典型特征是横流向与顺流向的控制频率接近，顺流向的位移显著增大。

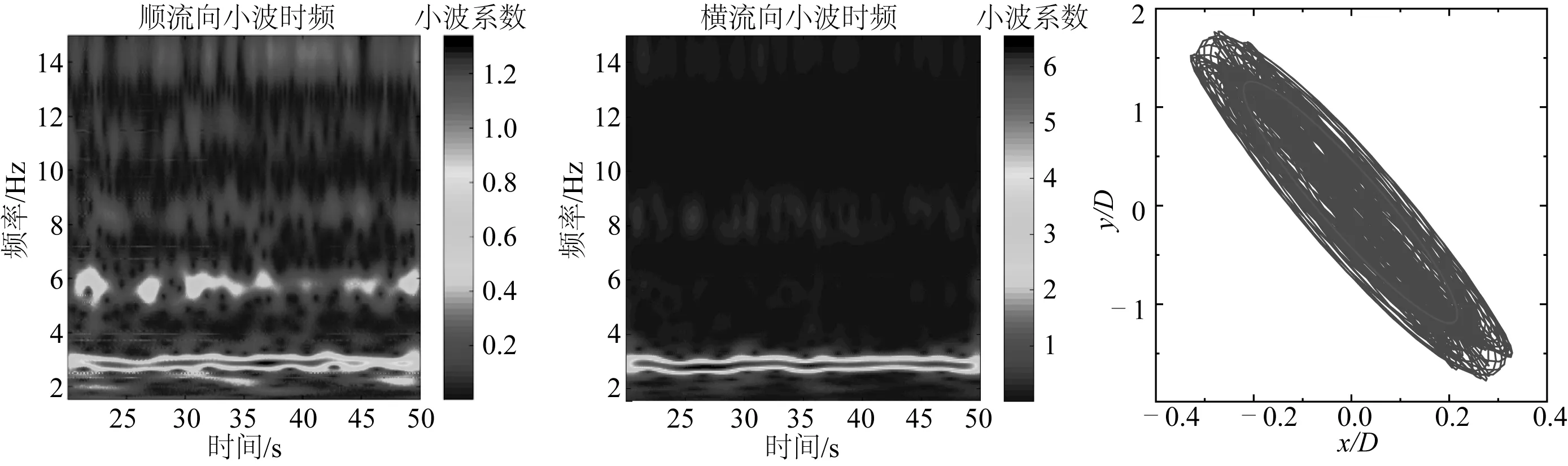
图11 交错布置时下游圆柱中点处横流向、顺流向位移的时频图与运动轨迹(S=6D，T=8D，Vr=7.52)Fig. 11 Time-frequency diagrams with respect to CF and IL displacement of middle measurement point along the downstream cylinder and x-y trajectories in a staggered arrangement

4 结 语

基于柔性圆柱多柱体流激振动试验，采用模态分析法将测量的应变信息转化为位移，分析了两根柔性圆柱在并列、串列、交错排布方式下的流激振动响应特性，得到以下结论：

1) 对于并列布置的柔性圆柱，间距比S/D≤ 6.0时两圆柱横流向振动存在显著的相互影响。两圆柱之间的相互作用使顺流向的位移增大，间距比S/D=8.0时两圆柱顺流向振动之间的相互影响仍然较强。

2) 柔性圆柱串列布置时，下游圆柱对上游圆柱的影响较小。受上游圆柱遮蔽效应的影响，同一流速工况下，下游圆柱的控制模态较低。由于柔性圆柱的多模态响应，下游圆柱的响应位移并未像串列刚性圆柱那样显著增大。

3) 柔性圆柱交错布置时，上游圆柱对下游圆柱横流向位移的影响较小，但对顺流向位移的影响较大。下游圆柱发生“Wake-flutter”，顺流向的位移显著增大，控制频率与横流向的控制频率相近，运动轨迹呈椭圆形。