基于GPU加速的Boussinesq类波浪传播变形数值模型

孙家文，朱 桐，房克照，刘忠波

(1. 大连理工大学 海岸和近海工程国家重点实验室 DUT-UWA海洋工程联合研究中心，辽宁 大连 116024； 2. 国家海洋环境监测中心，辽宁 大连 116023； 3. 大连海事大学 交通运输工程学院，辽宁 大连 116026)

作为一种典型的水波方程，Boussinesq类方程同时考虑色散性与非线性特征，能较准确地描述近岸海域波浪的传播演变过程，再现波浪在传播过程中出现的折射、绕射、散射、反射、浅水变形等物理现象。因此，Boussinesq方程被广泛应用于近海区域波浪的数值计算[1-2]。Peregrine[3]于1967年推导了适应变水深的二维Boussinesq方程，该方程被称为经典Boussinesq方程。但是该方程仅含有弱非线性和弱色散性项，难以适应大水深及非线性较强的问题。针对这类问题，Madsen和Sørensen[4]于1992年推导了二维扩展型Boussinesq水波方程(后称MS92方程)。该方程在动量方程中加入具有特定系数的三阶偏导数项，使得方程的色散性提高了一阶。因为MS92方程形式简单，又具有较好的色散性，得到广泛应用。

以Boussinesq方程建立的时域数值模型属于相位解析模型，为保证计算精度则需要较高的时间和空间分辨率。研究表明，单纯使用有限差分方法求解这类方程易产生高频数值震荡，影响计算的稳定性，通常需要采用具有耗散性质的光滑器以满足稳定性的需求[5-6]。利用有限体积法求解Boussinesq方程一定程度上可解决上述问题[7-8]。求解时，采用有限体积方法计算对流项，剩余项则采用有限差分方法求解，这一方式经过验证已经取得了较好的效果[9-10]。但是利用有限体积法离散对流项时，需要对界面左右变量进行状态重构和数值通量求解，过程较为复杂，耗时较高，当网格数目较多时更会大幅度增加计算时间。若想同时保证计算的精确性与高效性，单个主机的计算性能已经很难满足要求。采用主机与图形处理器相结合的方式搭建高性能计算平台是解决办法之一。迄今，众多CPU上的算法已成功移植到GPU上，计算效率得到了明显提升[11-12]。近两年，GPU已经开始使用到Boussinesq类模型的数值计算当中。Tavakkol[13]开发了一种基于GPU加速的Boussinesq类波浪模拟软件，不仅能提高计算效率，而且交互性强，提供了包含真实化渲染等很多可视性选项。Kim等[14]使用CUDA FORTRAN语言实现了Boussinesq方程模型的GPU并行化，计算效率相比CPU模型明显提升，最大加速比(CPU时间/GPU时间)可达20以上。GPU具有高并行性与强大的数据处理能力，能很好地解决当下数值模拟中网格数量多和计算效率低的问题。将来，采用GPU的海洋数值模型是海洋研究发展的重要方向之一。

利用CUDA C语言搭建基于GPU加速的Boussinesq类波浪传播变形数值模型，并模拟一系列经典工况，把所得的结果与解析解及CPU模型的模拟结果相比较，以验证模型的计算精度。除此之外，还比较了同种工况采用GPU模拟与CPU模拟的运算效率，得到了计算效率与网格数目之间的关系。

1 数学模型

1.1 控制方程

MS92方程的守恒形式如下[15]：

Ut+F(U)x+G(U)y=S(U)

(1)

式中：U为变量矢量，F和G为x与y方向上的通量矢量，定义为：

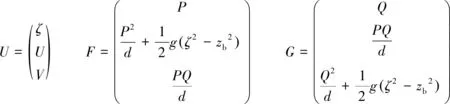
(2)

其中，

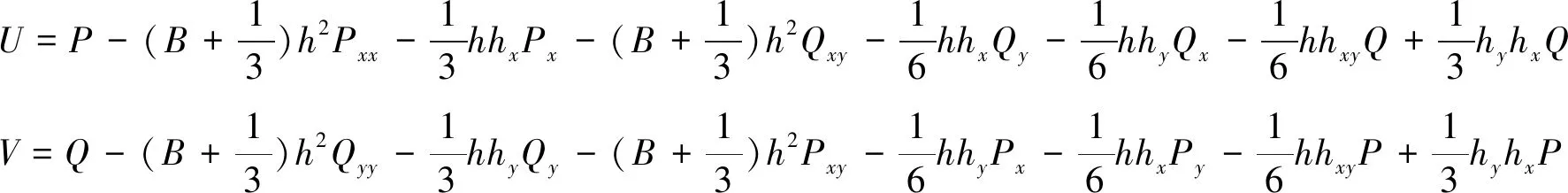
(3)

式中：d=η+h为总水深，η表示自由波面，h为静水水深，P和Q分别表示x和y方向上的速度通量(P=du和Q=dv，u、v分别表示x、y方向的水深平均速度)，B为色散性参数，取1/15。为实现海床变化和海岸水-陆动边界存在时高精度有限体积方法的和谐解，引入水位ζ=zb+d。式(1)中S为源项，可将其分成三个组成部分，分别为水底坡度项Sb、水底摩擦项Sf和色散项Sd，如下：

(4)

式中：色散项为：

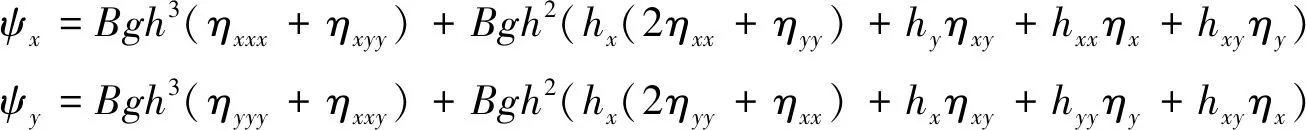
(5)

水底摩擦项：

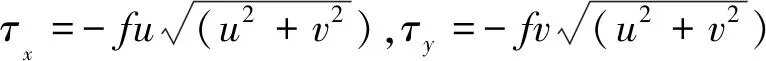
(6)

式中：f为底摩擦系数，取值范围为0.000 1～0.01，本文所有工况计算均未考虑海床摩擦。

1.2 方程空间离散、时间积分与模型边界条件

采用矩形网格单元，将计算域在空间、时间上均匀划分单元网格，波面η和速度u均定义在控制体中心。为了提高空间精度，采用四阶高精度状态差值方法(MUSCL)对界面左右变量进行重构，应用重构后的界面变量进行通量计算。模型的时间积分采用具有TVD性质的三阶龙格-库塔方法[16]。为保证计算收敛，时间计算步长由Courant-Friedrichs-Lewy(CFL)稳定性限制条件确定：

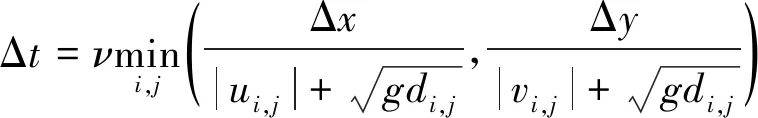
(7)

式中：ν为常数，这里取ν= 0.25。

对于文中计算工况，波浪通过给定初始条件或内部造波方法产生，计算域末端均为固壁边界，视情况不同在固壁前设置海绵层以吸收波浪能，以有效降低数值计算中的二次反射[15]。

2 GPU并行计算简介

在CUDA的并行计算模型中，CPU作为主机端，负责运行主程序并在运行过程中调用核函数。GPU作为设备端，主要进行线性化的并行计算。在设备端运行的函数被称为核函数。每个核函数对应的线程均以线程网格(grid)的形式存在，线程网格又被分成多个线程块(block)，每个线程块又由大量的线程(thread)组成。文中模型采用每个线程块1 024个线程的分配方案。

由于GPU无法直接读写内存中的数据，因此在核函数运行先需要初始化数据并将其由主机端传递到设备端的全局存储器中；之后，各个线程块会分配到不同的GPU大核 (Streaming Multiprocessors，简称SM)上，线程块上的不同线程交给GPU大核上不同的CUDA核心 (Streaming Processor，简称SP)来执行，从而达到并行运算的效果，如图1所示。为充分发挥GPU计算效率，在程序设计时，将主循环中计算耗时较重的模块，如状态重构、通量计算、时间积分等设计为核函数，在设备端运行。模型的初始化参数以及输入输出等模块在主机端部署。设备端和主机端之间通过CUDA C提供的内置函数(memcpy)进行数据传递，模型计算流程见图2。

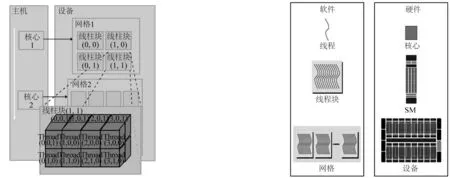
图1 CUDA编程模型Fig. 1 CUDA programming model

3 数值验证

针对所建立的GPU模型，通过几个典型工况的数值模拟分别对其进行验证。其中工况一为常水深孤立波的长距离传播问题；工况二为规则波跨越潜堤传播；工况三为封闭方形水池中的水面晃动；工况四为波浪在椭圆形浅滩上的传播。

3.1 孤立波在常水深水槽中的传播

在本工况中，x方向计算域长度为409.6 m，静水水深h0为1.0 m，在计算域内给出孤立波解析解作为初始条件，波高H=0.6 m，孤立波从计算域的左侧向右侧传播，初始时刻波峰位于x0=25 m处，网格尺寸Δx=0.2 m，忽略底摩擦的影响，且计算域边界处均采用固壁边界条件。图3给出了模拟的孤立波在t=0，10，20，30，40，50，60，70和80 s时的波面状态。从图中可见，经过长距离的传播，孤立波的波形和波高值均保持稳定，几乎未发生变化，说明数值离散正确，未引入额外的数值耗散和数值弥散。图4为时间t=80 s时，模型计算结果与解析解的比较，可以看出两者高度吻合，说明模型具有较好的精确性。

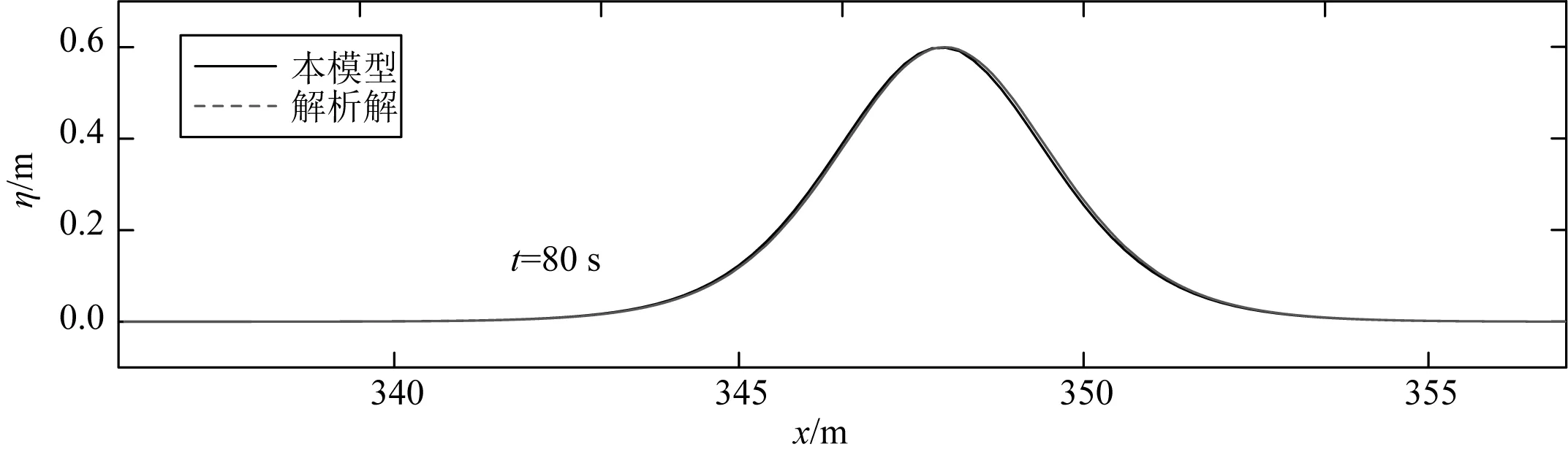
图4 t= 80 s时数值模拟结果与解析解的对比Fig. 4 Comparison of simulated and analytical surface profiles at t=80 s

3.2 规则波在潜堤海床上的传播

规则波跨越水下潜堤传播是非常复杂的波浪演化过程，涉及波浪的变浅、高次谐波产生释放等，该类试验被用来检验各类数值模型的色散性和非线性等综合性能。采用Dingemans[17]的规则波跨越潜堤传播的试验来对数值模型进行检验，试验海床设置如图5中所示，海床两端设置1.5倍波长海绵层吸收波浪，造波机在x= 0 m处，平底处静水水深为0.4 m，梯形坝的坡脚位于x=6.0 m处，梯形坝顶端长为2.0 m，距离静水面0.1 m，梯形潜堤前坡坡度为1∶20，后坡坡度为1∶10，根据Dingemans[17]的试验，在计算域内设置10个浪高仪，位置分别为x= 2，4，10.5，12.5，13.5，14.5，15.7，17.3，19和21 m。入射波波高H=0.02 m，周期T=2.02 s，计算网格长度为Δx=0.025 m。

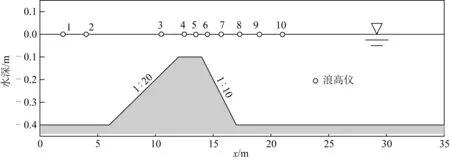
图5 规则波跨越潜堤传播试验布置Fig. 5 Experimental setup of regular waves propagation over submerged bar

图6给出了10个浪高仪位置上数值模拟结果与试验数据和CPU模型模拟结果的对比。如图6所示，规则波跨越堤顶传播过程中，水深变浅，波浪的非线性增强，高次谐波产生，波形发生明显变化，潜堤前以及堤顶位置处波面的数值计算结果与Dingemans的试验数据吻合程度高，说明GPU模型能够准确模拟规则波的传播及跨越潜堤时的波浪状态。堤后伴随水深的增加，各次谐波变成自由波，计算结果与实测值存在一定误差，这主要是方程捕捉高次谐波的色散性和非线性均不够造成的。整体来看，GPU模型与CPU模型的计算结果高度一致，验证了GPU模型的正确性。

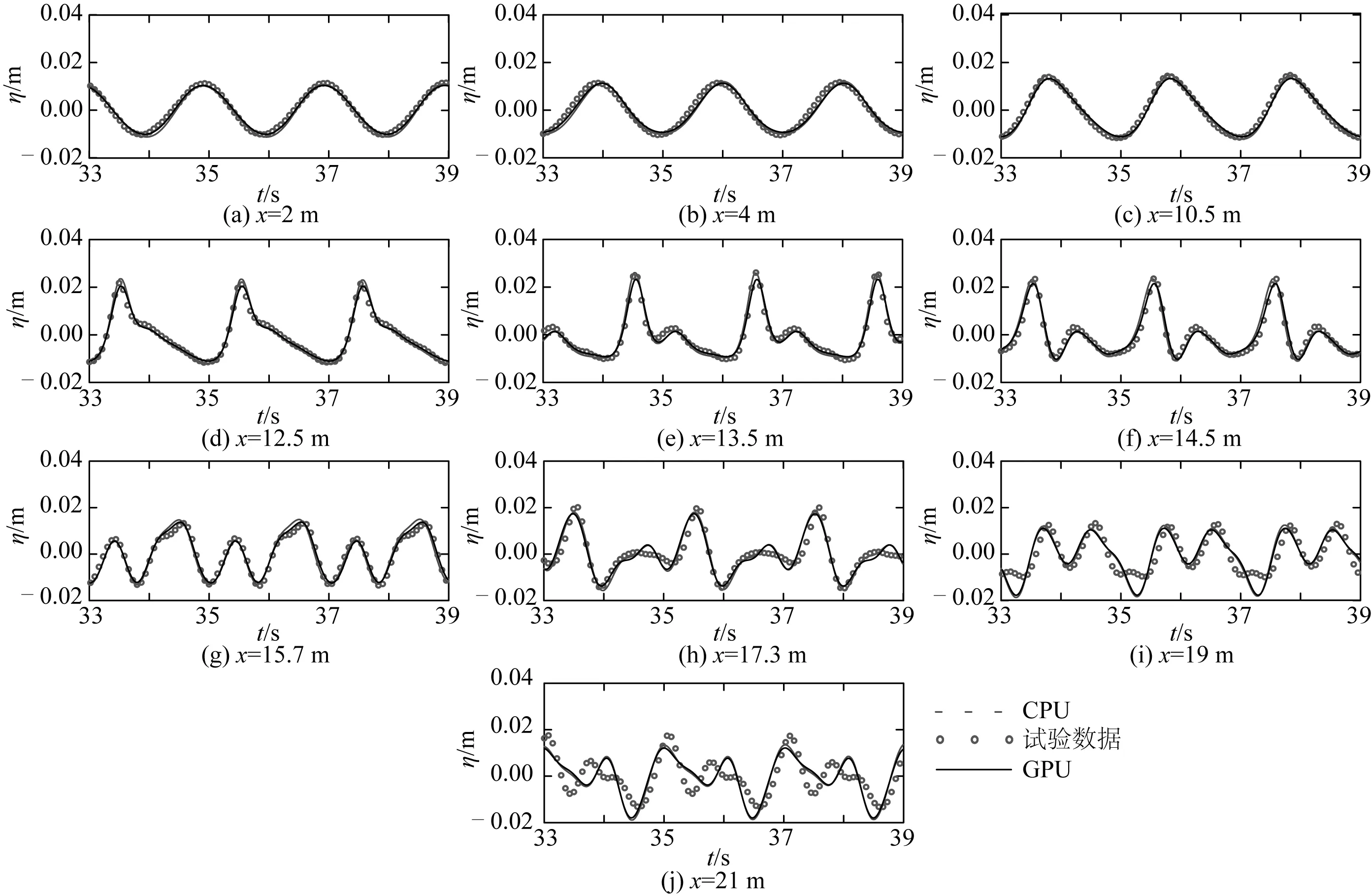
图6 规则波跨越潜堤传播各浪高仪处的波面时间序列Fig. 6 Time series of surface elevations for regular waves passing over a submerged bar

3.3 封闭方形水池中的水面晃动

为了验证模型精度以及对全反射边界的处理能力，对封闭方形水池中液体晃动进行了模拟。数值水池为正方形，尺寸为7.5 m×7.5 m，水深h= 0.45 m。水池四边为全反射直墙且与x、y轴平行，坐标原点位于水池左下角。网格尺寸Δx=Δy=0.058 593 75 m。初始波面为Gaussian形，即：

η0(x,y)=H0exp{-2[(x-a)2+(y-b)2]}

(8)

式中：a=b=3.75 m，H0=0.045 m。

图7给出了波面在一段时间后的分布情况。如图7所示，在t= 2 s时，波面关于x轴和y轴完全对称。经过比较长时间的传播后，在t=20 s时，对称性仍能很好地保持，说明模型离散和数值计算正确。

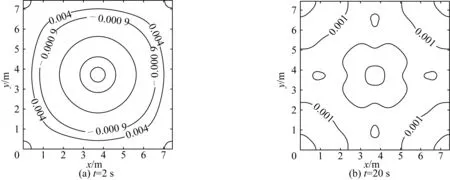
图7 t=2 s与t=20 s时波面分布Fig. 7 Free-surface contours at time t=2 s and t=20 s

图8给出了H0= 0.045 m时水池角点处和中心点处自由表面计算结果和线性理论结果的比较。波浪传播过程中前20 s内的非线性相对较弱，因而基于GPU加速的弱非线性Boussinesq数值模型与解析解结果基本一致。在后20 s内，伴随边界反射叠加，波浪的非线性增强，组成波成份增多，超出了方程本身非线性和色散性使用范围，导致二者存在一定的误差。

图8 H0=0.045 m时波面时间过程与线性理论计算结果比较Fig. 8 Comparison of time series of free surface elevation between numerical and theoretical results for H0=0.045 m

3.4 波浪在椭圆形浅滩上的传播

为了检验模型模拟复杂地形上波浪传播变形的能力，对Berkhoff等[18]所做的椭圆形浅滩上的波浪折、绕射物理模型试验进行了数值模拟。在模拟中，计算区域长30 m，宽20 m，具体试验地形如图9所示。

模拟波浪入射波高为H0=0.046 4 m，周期T=1 s，在x=3 m处沿x轴正向入射。上下两边界(y=0 m和y=20 m)为全反射边界，左侧海绵层宽度为2 m，右侧海绵层宽度为3 m。网格数目为512(x方向)×256(y方向)=131 072。模型运行时间为40 s。

将GPU模型计算结果与Tonelli和Petti[8]计算结果进行了对比，见图10。可见，本模型的数值计算结果与Tonelli和Petti[8]所得结果基本一致，说明本模型可以较好地模拟波浪的折射和绕射等现象。

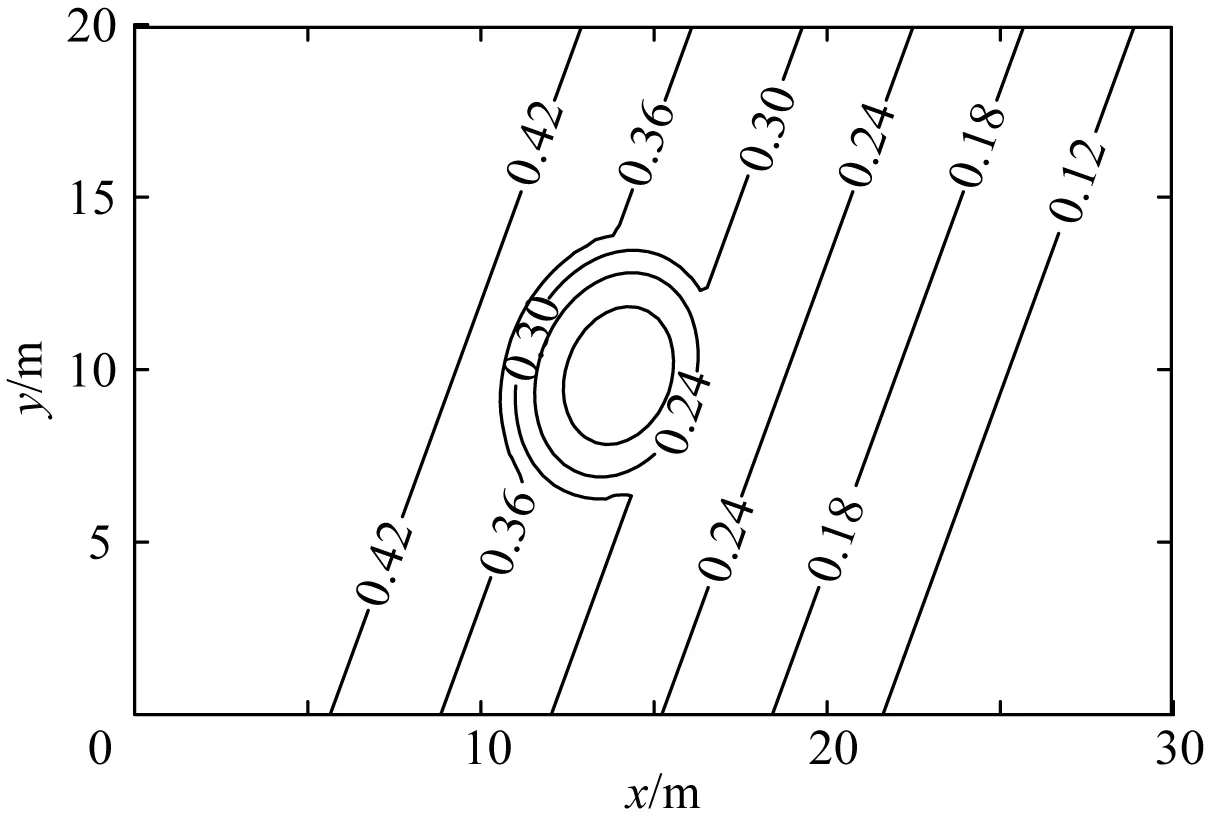
图9 试验地形图(Berkhoff等[18])Fig. 9 Topographic map of experiment (Berkhoff, et al [18])

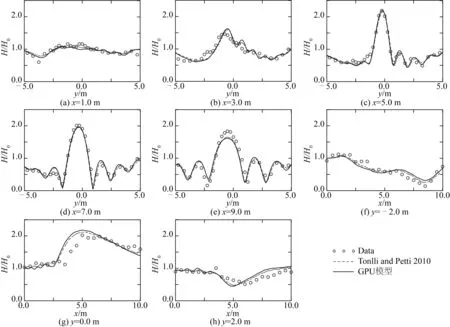
图10 GPU模型计算波高与试验数据和他人结果比较Fig. 10 Comparisons of normalized wave height from GPU model, data and other simulation

4 GPU并行模型加速性能分析

本文计算使用专业图形加速卡Tesla k20进行，为了对比也使用CPU模型进行了计算。

具体设备参数和开发平台如下：

CPU：Intel i5 8500，主频3.0 GHz，含6个CPU核心。

GPU：专业图形加速卡Tesla k20，含2 688个流处理器，主频732 MHz，单精度浮点性能3.95 Teraflops，显存5.2 GHz 6GB，带宽250 GB/s。

开发平台：Intel Complier Visual studio 2015，CUDA 8.0。

利用同一台设备分别使用GPU模型与CPU模型进行计算，统计计算时间，并计算出加速比(CPU模型计算时间TC与GPU模型计算时间TG之比)，具体结果见表1。从表1可知，随着网格数增加，加速比稳定提高。同时，不同的工况中的加速比一般不同，其中封闭方形水池的水面晃动所达到的加速比最大，计算效率的提升最为明显，最大加速比可达12.72。综合来看，GPU并行模型的确对计算效率有很明显的提升。

Kim等[14]发展的GPU类Boussinesq模型加速比可达20，高于本文建立模型，可能是如下原因所致：1)图形处理器不同，本文选用的图形处理器是NVIDIA GeForce Tesla k20，Kim等选用的是NVIDIA GeForce GTX TITAN Z；2)编程框架不同，本文的编程语言是CUDA C，而Kim等选择的是CUDA FORTRAN；3)计算工况不同，工况的差异会影响加速比，这在本文中已经得到了证明；4)算法不同，不同的算法由于数据读取方式的不同，会对计算效率有着较大影响。

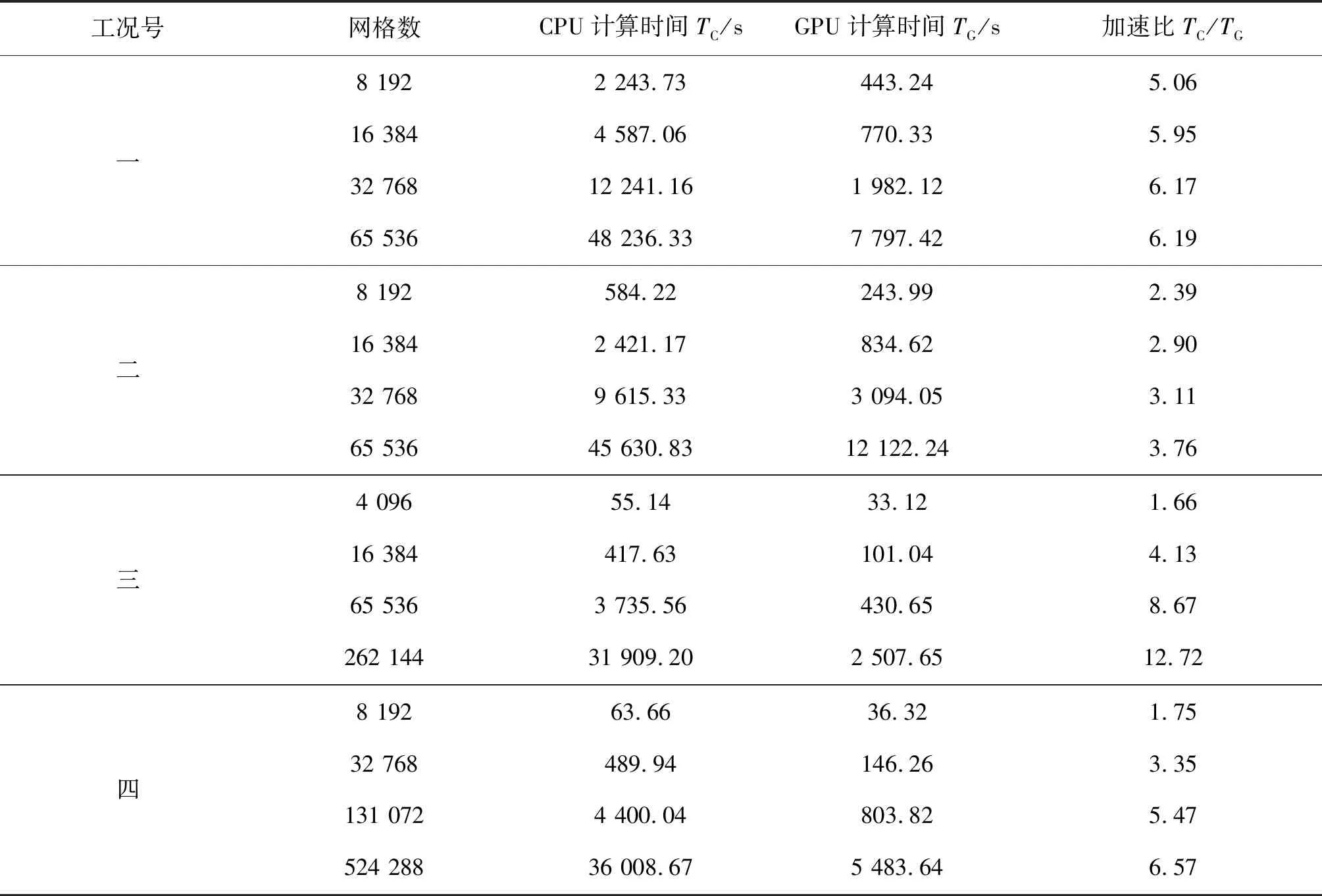
表1 各工况CPU模型与GPU模型计算效率比较Tab. 1 Computational efficiency comparison between CPU model and GPU model

5 结 语

利用CUDA C语言与图形处理器(GPU)实现了Boussinesq模型的并行化。采用有限差分与有限体积的混合格式来求解方程。在计算过程中，通过把较为复杂的计算任务分配到GPU上分块并行处理，从而实现大大提升计算效率的目的。将本模型的计算结果与CPU模型上的计算结果和模型本身的解析解相比较，所得结果基本一致，验证了本模型计算的正确性。同时对本模型与CPU模型的计算效率进行了对比。通过比较发现，本模型对计算效率有很明显的提升，文中工况的最大加速比可达12以上。

进一步的研究将围绕不同图形处理器设备加速性能、并行优化以及实际应用方面展开。