剑杆织机打纬凸轮接触碰撞力建模与仿真

魏 展， 金国光， 李 博， 宋艳艳， 路春辉

(1. 天津工业大学 机械工程学院， 天津 300387；2. 天津工业大学 天津市现代机电装备技术重点实验室， 天津 300387)

剑杆织机在高速运行时，打纬机构中凸轮与滚子的接触碰撞现象不可避免，由此带来的动力学问题影响着机构整体动力学性能和凸轮寿命。碰撞过程因其作用时间短、强度高，给系统动力学性态造成了巨大影响，已经成为系统分析和控制中不可忽略的重要因素，同时也给多体系统动力学建模和数值仿真带来了一定的困难。由于碰撞过程的高度复杂和非线性，目前对于该问题的研究还远未达到与连续动力学相同的水平，这类问题的研究不论对理论研究的进展还是对工程问题的解决都具有十分重要的意义和价值[1]。

国内外学者对于机构碰撞[2-3]和多体系统碰撞问题[4-5]研究较多，尤其对于轴承及旋转铰的接触碰撞研究更为广泛[6-8]。近几年对织机开口、引纬机构的运动学和动力学研究也取得了新的进展[9-10]。凸轮机构作为稳定高效且广泛应用的机构，对其接触碰撞模型研究较为欠缺，而对于打纬凸轮机构碰撞问题的研究则更加少之又少。在高速含间隙的凸轮机构运动中，接触碰撞力对于机构动态性能及表面寿命的影响尤为重要。建立简单有效的凸轮副接触碰撞模型是研究碰撞力对机构影响的基础，也是建立完善的凸轮机构动力学模型的关键。本文基于改进的Lankarani-Nikravesh(L-N)碰撞力模型[11-12]，建立凸轮副接触碰撞模型，并研究初始碰撞速度对接触碰撞力大小的影响。

当前，对运动副接触碰撞研究基本都是单纯应用Hertz接触理论研究接触处变形及应力，或应用有限元软件进行仿真研究[13-14]，研究对象也主要集中在传统运动副。以一般性打纬凸轮机构为研究对象，建立凸轮-滚子副接触碰撞模型，对于深入了解碰撞力对打纬机构冲击影响具有直接意义，也为精确建立打纬凸轮机构整体动力学模型提供参考。

1 接触碰撞力模型

目前，国内外学者广泛研究和应用的接触碰撞力模型主要包括：考虑能量损耗的Kelvin-Voigt线性黏弹性模型，纯弹性理论Hertz接触力模型，基于Hertz接触理论和恢复系数的L-N非线性弹簧阻尼模型，以及我国学者白争锋对L-N模型进行修正之后的混合模型[15-16]。这些模型都根据实际情况考虑到碰撞体几何和材料特性、碰撞速度和能量损耗等因素。合适的接触碰撞力模型是进行机构接触碰撞力和动力学性能研究的关键。

1.1 L-N接触力模型

L-N接触碰撞模型是基于通用的Hertz接触力模型而建立的，充分考虑了材料阻尼的影响，且模型中包含了撞击速度，考虑了间隙对接触碰撞力的影响。该模型在等效刚度和等效阻尼参数选择合理时具有较高的计算精度，表达式为

(1)

式中：P为接触点法向接触碰撞力，N；K为系统等效接触刚度，N/m；δ为接触体在接触点的法向压缩量，m；n为指数，且大于或等于1，一般取1.5；Fk为弹性恢复力，N；Fc为阻尼力，N；C(δ)为与δ有关的碰撞阻尼系数，可表示为

C(δ)=ηδn

(2)

式中，η为黏滞阻尼因子。假设能量损失是由于碰撞体的材料阻尼引起的，能量将以热的形式损耗，可由能量损耗公式和接触力沿黏滞环的环路积分公式相等得到：

(3)

式中：ce为恢复系数；v0为撞击点在撞击初始时刻的相对速度，m/s。

接触碰撞力表达式可表示为

(4)

由于L-N接触碰撞模型能够反映接触碰撞过程中的能量损失行为，且全面包含了碰撞体材料属性、局部变形、碰撞速度等信息，因此，该模型被国内外学者广泛应用。

1.2 修正的接触碰撞力混合模型

我国学者白争锋以间隙铰为研究对象[17]，基于L-N接触碰撞模型，对其中的接触刚度K和阻尼系数C(δ)进行了修正，得到刚度系数

(5)

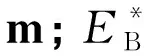
修正的阻尼系数为

(6)

该阻尼系数不受碰撞恢复系数的限制，适用于不同恢复系数的材料。

最终得到了旋转铰间隙接触碰撞力混合模型的表达式：

(7)

2 打纬凸轮系统接触碰撞力模型

打纬机构的核心为凸轮-滚子机构，研究打纬凸轮碰撞问题的实质为凸轮盘与滚子之间接触碰撞问题。选取共轭凸轮中主凸轮盘为研究对象，碰撞过程中与滚子之间的运动关系如图1所示。即转变为硬质光滑的凸轮-滚子接触碰撞力模型。

图1 打纬凸轮-滚子机构模型Fig.1 Model of beating-up cam-roller mechanism

因白争锋修正的接触碰撞力混合模型采用了先进的弹性接触模型和阻尼系数，具有较高的计算精度和较广的适用范围，因此，建立凸轮滚子接触力模型时，以此模型为基础并进行修正。

作为凸轮滚子接触模型，因接触处分凸-凸接触与凹-凸接触，故式(5)变形为适用于凸轮副和旋转铰的一般性接触刚度系数表达式

(8)

假设某特定工况下碰撞区域为凸-凸接触，则凸轮副接触刚度系数为

(9)

式中：b为凸轮和滚子的接触宽度，m；δ为接触体在接触点的法向压缩量，m，即为碰撞力的作用行程，应包含凸轮、滚子的法向变形量；R1为接触处凸轮曲率半径，m；R2为滚子外轮廓半径，m；E*为接触弹性模量，Pa，其计算公式为

(10)

式中：E1为凸轮弹性模量，Pa；E2为滚子弹性模量，Pa；μ1为凸轮泊松比；μ2为滚子泊松比。

因此，可得凸轮滚子系统接触碰撞力

(11)

式中，系统等效阻尼系数

(12)

式中，ce为恢复系数，一般取0.9。

3 接触碰撞动力学模型

在滚子竖直向下撞向凸轮的碰撞过程中，以弹性变形大小δ为广义坐标，根据Newton/Euler法建立滚子动力学方程：

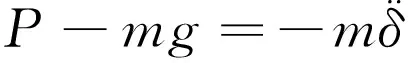
(13)

式中：m为滚子质量，g；g为重力加速度，m/s2。将式(11)代入式(13)得：

(14)

解上述动力学方程即可求得打纬凸轮-滚子系统碰撞过程中碰撞力及碰撞变形曲线。

4 碰撞力和碰撞变形的求解与仿真

已知某打纬凸轮机构中，碰撞点凸轮盘曲率半径R1为0.1 m, 滚子半径R2为0.05 m, 凸轮弹性模量E1为200 GPa，滚子弹性模量E2为200 GPa，凸轮和滚子密度ρ均为7 900 kg/m3，凸轮泊松比μ1为0.3，滚子泊松比μ2为0.3,碰撞初速度v0为1 m/s，碰撞区域宽度b为0.02 m。根据式(11)和式(14)以及上述已知条件，计算可得碰撞力及碰撞变形量变化曲线，如图2所示。

将凸轮-滚子机构应用瞬态碰撞分析软件ANSYS/LS-DYNA进行离散化，结果如图3所示。对其附加约束、载荷和初始速度等已知条件后进行求解。利用仿真结果可视化软件LS-PrePost可展示碰撞过程中机构各处应力及变形，结果如图4所示。

因LS-PrePost软件无法直接得出凸轮-滚子间碰撞变形量，故采用标记滚子和凸轮轴心连接线上非变形点(N16、N1360)方式(如图5所示)通过计算2点位移差的方法得出凸轮-滚子间碰撞变形量。

仿真得出的变形量与MatLab软件计算的变形量进行对比，结果如图6所示。可看出仿真与计算的变形量基本一致，说明建立的接触碰撞力模型的正确性。

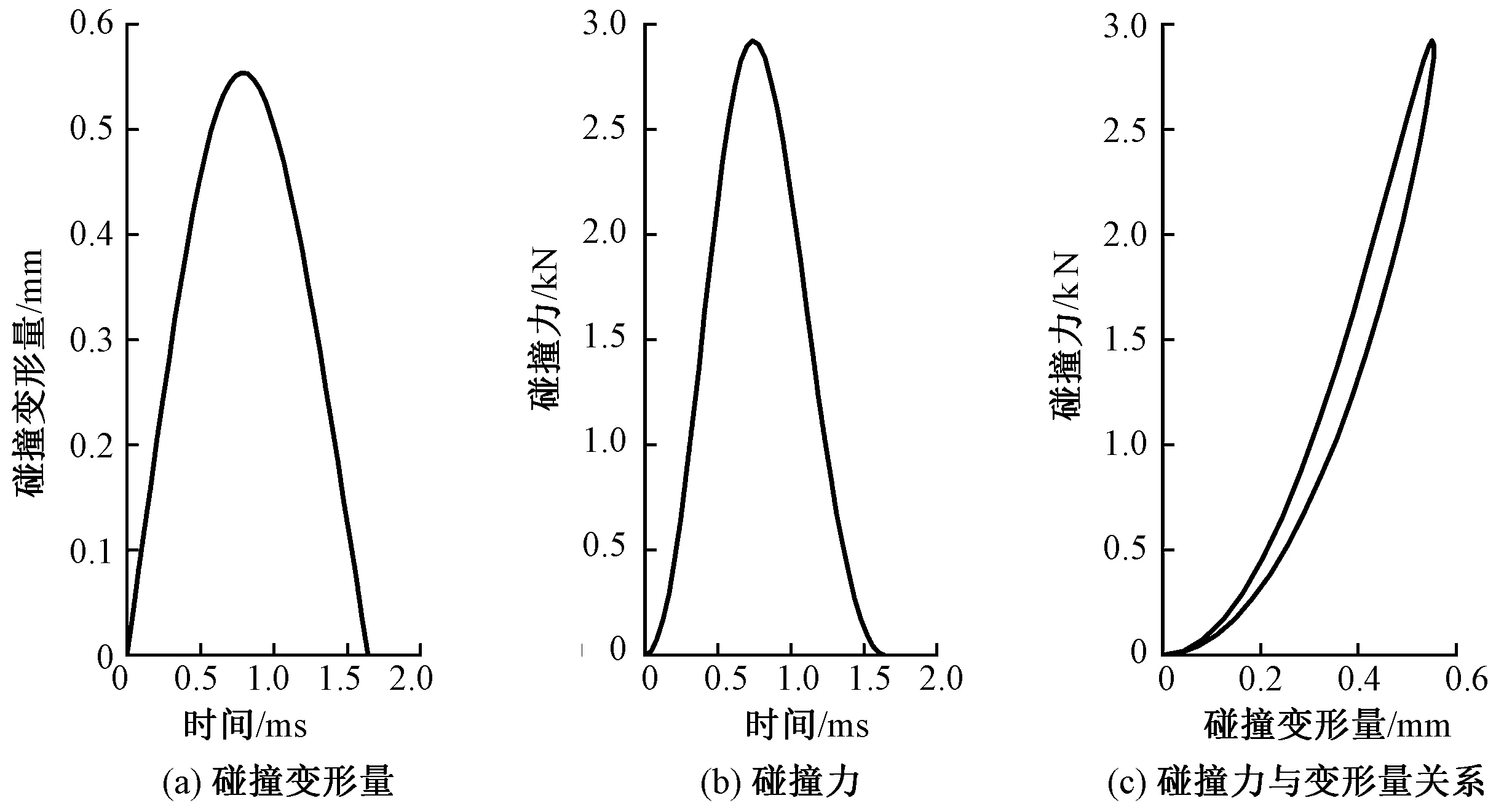
图2 碰撞力与碰撞变形量Fig.2 Collision force and collision deformation. (a) Collision deformation; (b) Collison force; (c) Relationship between collision force and deformation

图3 凸轮-滚子机构离散化Fig.3 Discretization of cam-roller mechanism

图4 碰撞过程模拟仿真Fig.4 Simulation of collision process

图5 滚子和凸轮标记点Fig.5 Mark points of roller and cam

图6 碰撞变形量仿真与计算结果对比Fig.6 Comparison of collision deformations between simulation and calculation

5 影响碰撞动态响应的因素

碰撞力和碰撞变形量的大小取决于碰撞体相对速度、材料属性及碰撞区域几何特征等因素，现分别研究碰撞速度和碰撞点凸轮曲率半径的变化对碰撞动态响应的影响。

5.1 初速度的影响

分别取碰撞初速度v0为1.0、1.5、2.0、2.5、3.0 m/s，计算得出5种情况下的碰撞力和碰撞变形(如图7所示)，所对应的接触碰撞作用时间分别为1.642、1.435、1.303、1.211、1.140 ms。可见，随着碰撞初速度的增加，碰撞时长随之减小。

图7 5种碰撞初速度下碰撞力和碰撞变形量Fig.7 Collision force(a)and collision deformations (b) at five kinds of initial collision speed

图8 最大碰撞力和最大碰撞变形量随碰撞初速度变化规律Fig.8 Variation of the maximum collision force and deformation with initial collision speed

最大碰撞力和最大碰撞变形量随碰撞初速度的变化规律如图8所示。可以看出，随着碰撞初速度的增加，最大碰撞力和最大碰撞变形量基本呈线性增大。此工况下，初速度增大为原来2倍时，最大碰撞力增大为原来的2.52倍，最大碰撞变形量增大为原来的1.59倍。

5.2 碰撞点曲率半径的影响

不同凸轮或不同工况下碰撞点凸轮曲率半径并非固定值，现保持碰撞初速度v0=1.0 m/s不变，分别取凸轮曲率半径R1为0.1、0.2、0.3、0.4、0.5 m，计算得出5种情况下的碰撞力和碰撞变形(如图9所示)，所对应的接触碰撞作用时间分别为1.642、1.786、1.888、1.970、2.037 ms。可见，随着凸轮曲率半径的增加，碰撞时长随之增加。

图9 5种碰撞点凸轮曲率半径下碰撞力和碰撞变形量Fig.9 Collision force(a)and collision deformations (b) at five kinds of cam radius for collision point

最大碰撞力和最大碰撞变形量随凸轮曲率半径变化规律如图10所示。可以看出，随着凸轮曲率半径的增加，最大碰撞力随之减小，最大碰撞变形量随之增加。凸轮曲率半径增大为原来2倍时，最大碰撞力减小为原来的0.92倍，最大碰撞变形量增大为原来的1.09倍。可见，较之碰撞初速度，凸轮曲率半径变化对最大碰撞力和最大碰撞变形量的影响并不明显。

图10 最大碰撞力和最大碰撞变形量随曲率半径变化规律Fig.10 Variation of maximum collision force and deformation with radius of curvature

6 结 论

1) 基于L-N接触碰撞模型，并进行修正后应用于打纬凸轮系统，最终建立的凸轮-滚子系统动力学碰撞模型具有形式简洁、计算方便、实用性强等特点，能较为准确地描述打纬凸轮碰撞过程动力学特性，是行之有效的系统碰撞动力学模型。

2) 碰撞过程是构件整体和局部运动状态在瞬态发生突变，建立的碰撞动力学模型难以通过实验或有效仿真手段验证。应用瞬态碰撞分析软件ANSYS/LS-DYNA并配合可视化软件LS-PrePost，通过计算滚子和凸轮轴心连接线上非变形点位移差的方法得出打纬凸轮与滚子间碰撞变形量，是进行碰撞仿真验证的有效手段。

3) 仿真结果表明，碰撞初速度和凸轮碰撞点的曲率半径都会影响碰撞过程动态响应，碰撞初速度对打纬凸轮系统碰撞过程的碰撞力和碰撞变形量影响更为明显，因此，抑制碰撞损伤应主要针对避免或降低碰撞初速度实施措施。运动副存在间隙必然导致高速运动下产生相对碰撞初速度，在打纬凸轮制造和装配过程中应克服制造和装配误差带来的凸轮副间隙。