凸轮检测方法的误差分析

申涛，刘兴富

（1.西安工业大学，陕西西安 710032;2.广州威而信精密仪器有限公司，陕西西安 710075）

1 概述

笔者提出的“敏感点法”，在发动机凸轮检测中已被普遍采用。分析表明，“敏感点法”不但测算过程简便，而且能满足发动机凸轮的精密检测要求。“敏感点法”所获得的升程误差检测数据，在实际运用中符合“最小条件”要求。它是目前凸轮精密检测的理想方法之一。

2 检测方法原理

“敏感点法”是在“对称最佳”原理的基础上建立起来的。具体方法是:在凸轮“桃尖”两侧各任选一点a（αa，ha，h'a）和b（αb，hb，h'b），作为确定凸轮检测位置的基准。由点a、b的理论正确升程ha、hb确定出点a、b的实际转角φa、φb。理论和实践均证明，当点a、b选在凸轮两侧的“敏感点”时，可以获得凸轮的理想检测位置，如图1所示，其中上角*为等值误差点。

凸轮检测起始转角φ0由以凸轮两侧“敏感点”为基准［1］求出

在凸轮检查仪上按间隔点 （步长一般取为1°）进行检测，得出凸轮的升程检测数据。

下面对“敏感点法”的误差进行分析:点a、b的升程误差，可由升程函数表达式的全微分求得

点a、b的形状误差，必然影响式 （1）的正确性。如果将点a、b取在凸轮两侧的“敏感点”m、n时，并令Δhm=Δhn，可由式 （3）得到

式（1）～（4）中:

Δα为凸轮起始转角误差;

αm、αn为凸轮左、右侧“敏感点”的理论转角;

Δrm、Δrn为凸轮左、右侧“敏感点”的形状误差;

hm、hn为凸轮左、右侧“敏感点”的理论升程;

h'm、h'n为凸轮左、右侧“敏感点”的升程变化率。

由式 （4）可知，Δ的大小不仅取决于点a、b形状误差的大小和方向，更重要的还取决于点a、b在凸轮轮廓上的位置。分析式 （4）:

（1）分子项越小，分母项越大，Δα越小。

（2）由分子项 （Δrm－Δrn）可以看出，Δα的大小与凸轮左、右侧“敏感点”处的形状误差有关。笔者在测量实践中发现，当凸轮处于理想检测位置时，凸轮左、右侧“敏感点”的升程误差一般均为负值，这也就是加工中常说的“凹陷现象”，这是由于“敏感点”是切削速度和压力角变化的转折点的缘故。在一定加工工艺条件下，凸轮左、右侧“敏感点”处的形状误差，产生的是同向误差，且差值甚小，分子项最小;由分母项 （h'm－h'n）可以看出，因为凸轮左、右侧“敏感点”的升程变化率的符号相反，绝对值最大，显然，只有将点a、b取在凸轮左、右侧的“敏感点”时，分母项最大。所以，这时Δα最小。

（4）综上所述可知，“敏感点”是确定凸轮检测位置的最理想的基准［2］之一。

3 凸轮检测位置误差引起的升程误差

发动机凸轮的升程误差，是凸轮形状误差的反映。检测时，凸轮的理想形状相对于实际形状的位置应按“最小条件”来确定。即应使所获得的检测数据能保证凸轮升程误差的最大值为最小。

如若被测凸轮是理想凸轮 （图2）。设点c为凸轮理论转角起始点，当测头与点c相接触，凸轮绕旋转中心O转过α角度时，测头与凸轮轮廓上点d相接触，升程为hd（图2（a））;如果将凸轮旋转一微小角度Δα，以点c1为凸轮检测转角起始点，仍转过α角度时，测头则由与点c1相接触到与凸轮轮廓上点d1相接触，测得的升程为hd1（图2（b）），这时，由凸轮检测位置误差引起的误差为

Δh0=hd1－hd

由于假设被测凸轮是理想凸轮，很显然，误差仅仅是由凸轮检测位置误差引起的

Δh0=h'·Δα

对于有形状误差的被测凸轮，误差是形状误差 （通常由随机误差构成）与检测位置误差 （属于系统误差）的叠加，即

式中:Δr为凸轮轮廓的形状误差;

h'为凸轮升程变化率;

Δα为凸轮检测位置误差。

综上所述，凸轮检测位置误差引起的误差，具有如下规律:

（1）理想凸轮的误差，纯粹是由于凸轮检测位置误差引起的;有形状误差的被测凸轮误差是凸轮形状误差与检测位置误差引起的误差的叠加。

（2）当被测凸轮的检测位置确定之后 （Δα已知），检测位置误差引起的升程误差，凸轮轮廓上各被测点误差大小各不相同，其值取决于各被测点升程变化率的大小。

（3）对整个凸轮而言，升程变化是非线性的，而对某一被测点则是线性的。

正确确定凸轮检测位置的目的，是为了消除凸轮位置误差的影响，实现凸轮真实形状的反映。因此，检测时必须使式（5）第二项中的Δα=0。当然，要做到这一点，是相当困难的。但是，在实际检测中，“敏感点法”可以把Δα控制在非常小的范围之内。使凸轮检测位置误差引起的误差忽略不计。

4 凸轮检测系统误差引起的升程误差

凸轮升程测量方程式可表达［3］为

对式 （6）微分

分析式 （7）可知，式中第一项Δα是由四部分组成:凸轮检测位置误差;被测凸轮偏心误差;拨杆设计或安装不合理引起的误差;角度仪器的误差。第二项中的=1，所以Δr0（基圆母线的形状误差）等值地反映升程误差。

限于篇幅，文中不对式 （7）中第一、第二项进行分析，仅对第三、第四项具体分析如下。

4.1 检测仪器误差引起的升程误差

凸轮的检测，是由长度和角度仪器组成的检测系统进行的。测量仪器误差引起的升程误差为

式中:h为凸轮被测点的升程;

h'为凸轮被测点的升程变化率;

φ为角度仪器的转角。

4.2 被测凸轮偏心引起的升程误差

当选用滚柱测头 （0＜rp＜∞）时

当选用刀口测头 （rp=0）时

当选用平面测头 （rp=∞）时

式中:e为凸轮基圆偏心距;

r0为凸轮基圆半径;

rp为测头半径;

α为凸轮转角;

θ为凸轮基圆偏心方向角;

h为凸轮被测点升程;

hmax为凸轮最大升程;

h'为凸轮被测点的升程变化率。由式 （10）、（11）可知，Δh2是由转角误差和偏心误差引起的误差的和。当偏心方向角θ和被测凸轮升程变化率的绝对值较大的一侧敏感点的位置相差90°时，由偏心误差引起的升程误差最大。

4.3 杆设计安装不合理引起的升程误差

被测凸轮安装在角度仪器的头尾顶针之间，由于被测轴线与仪器主轴轴线不重合 （如图3所示），当拨杆设计或安装不合理时，被测凸轮将产生一个转角误差而引起升程误差［4］

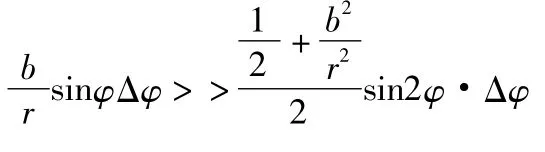
则

式中:b为拨杆球心与主轴顶尖间的轴向距离;

r为拨杆球心与主轴顶尖间的径向距离;

φ为角度仪器的实际转角;

Δφ为被测凸轮轴线与仪器主轴轴线间的夹角;

h'为凸轮被测点的升程变化率。

分析式 （12）可知:b≠0时，当 φ=0°、φ=180°时，Δh3=0;当φ=90°、φ=270°时，Δh3取得最大值;b≈0时，Δh3≈Δφ2。因此，拨杆的正确设计与安装应引起特别重视。

4.4 测头制造及安装误差引起的升程误差

检测对心式凸轮机构凸轮的升程时，应保证测头中心、测量轴线、凸轮旋转轴线处在同一平面，并保证测量轴线和凸轮旋转轴线垂直。

（1）平面测头垂直度、平面度误差引起的升程误差。

当测头平面不垂直于测量轴线以及测头的平面度误差 （图4）引起的升程误差

由于测头的平面度误差与其引起的误差等值，所以

式中:hc为被测点的升程检测值;

h'为被测点的升程变化率;

Δc为平面测头的垂直度误差;

Δp为平面测头的平面度误差。

（2）滚柱测头半径误差引起的升程误差。

现以S195型柴油机的供油凸轮为例，由式 （8）可得:

凸轮轮廓的直线段 （0°≤α≤30°56'48″）

凸轮轮廓的顶圆段 （30°56'48″≤α≤63°22'10″）

凸轮轮廓的腹圆段 （63°22'10″≤α≤170°07'28″）

式中:α为凸轮转角;

αc=54°50'50″为凸轮桃尖理论转角;

αmax=170°07'28″为凸轮升程部分最大理论转角;

Δrp为测头半径的误差;

ld为基圆至顶圆中心距;

lf为基圆至腹圆中心距。

凸轮轮廓的基圆段 （170°07'28″≤α≤360°）是基准，其误差为零。

（3）滚柱测头 （刀口测头）中心线和凸轮旋转轴线不共面引起的升程误差。

由图5可得

因为

所以

式中:r0为凸轮基圆半径;

rp为测头半径，刀口测头时rp=0;

h为被测点的理论升程;

hc为被测点的升程检测值;

Δ为凸轮旋转中心与测头中心移动轨迹平面间的距离。

4.5 检测系统不符合阿贝原理引起的升程误差

在凸轮检测中，无论是平面测头还是滚柱测头，测头和凸轮的接触点，除基圆部分、“桃尖”外，凸轮轮廓的其他部分均不通过测量轴线。当接触点偏离测量轴线时，检测系统不符合阿贝原理 （图6），由此引起的误差为

当选用平面测头时，p=h'

式中:p为接触点偏离测量轴线的距离;

l为测头中心至前支承的间距;

L为测轴两支点的间距;

Δb为测轴配合最大间隙。

5 凸轮检测方法标准误差

当检测系统、被测凸轮、测头制造、安装及测力、温度等因素引起的升程误差在某一定范围时，可求出凸轮检测方法的标准误差［5］:

当用平面测头时

当用滚柱测头时

当用刀口测头时

凸轮检测方法的极限误差:

6 结束语

在JJ2—JJF2数字显示式凸轮测量仪 （角值 1″，线值1 μm）上测量凸轮的升程，以普遍应用的S195型柴油发动机圆弧凸轮为例，对凸轮检测方法的误差进行了分析。应该说明，文中方法对于发动机高速领域中的各种函数凸轮同样适用。

【1】刘兴富.试论凸轮检测起始转角的求解方法［J］.台北:机械技术，2002（12）:145－150.

【2】刘兴富.凸轮检测数据的基准转换处理方法［J］.制造技术与机床，2001（9）:29－33.

【3】刘兴富.发动机凸轮误差测量数据的计算机处理方法［J］.汽车零部件，2008（6）:69－72.

【4】刘兴富.试论凸轮测量步长的优化设计方法［J］.汽车零部件，2011（1）:60－61.

【5】刘兴富.凸轮轴自动测量仪精度认定方法的探究［J］.汽车零部件，2011（8）:64－67.