起伏振动下倾斜管内单相流流动阻力特性分析

2020-05-07周云龙刘起超汪俊超

原子能科学技术 2020年3期

周云龙，刘起超，汪俊超

(东北电力大学能源与动力工程学院，吉林省吉林市 132012)

21世纪以来，环境问题和能源危机一直是制约社会发展的“紧箍咒”，核能具有高效、稳定和可控的优点，被各大国家所青睐。2010年9月，俄罗斯第1座浮动核电站下水。2016年11月，我国首座海上核电站开工，并计划在南海建设20座。海上核电站在运行过程中必然受到海浪的影响而处于起伏振动状态，此时核电站一回路的冷却液流动也处于起伏振动状态，一旦错误估计一回路的冷却液流动阻力，会影响反应堆的冷却效果，造成严重的安全事故。因此，正确分析和计算起伏振动状态下单相水的流动阻力，对海上核电站的安全运行至关重要。

目前关于稳定状态下单相流动的阻力计算方法的研究已非常成熟，尼古拉斯公式和莫迪图均能用于单相流动阻力的计算[1]。非稳定状态下单相流动阻力的研究相对还较少，高璞珍等[2]对海洋条件下的核动力装置一回路冷却剂的流动进行建模，分析了冷却剂的受力情况，得出了非稳定状态下流动附加压降的计算公式，为非稳态流动阻力特性的研究奠定了理论基础。Yan等[3-4]对流动进行简化，建立了摇摆状态下单相水流动特性的理论模型。张金红等[5]对摇摆状态下内径34.5 mm的有机玻璃管内单相水的摩擦压降特性进行了实验研究，应用能量方程和Darcy公式求解摩擦系数，进而拟合出用于计算摇摆状态下单相水的摩擦阻力系数的计算公式。栾锋等[6]通过实验研究了不同管径水平管单相水的阻力特性，发现摇摆状态下单相水摩擦压降也呈现周期性波动，波动周期与摇摆周期一致，并分析了摇摆周期、摇摆幅度、雷诺数和管径对摩擦系数的影响，给出了摇摆状态下单相水摩擦系数的计算公式。幸奠川等[7-12]对摇摆状态下单相强制循环层流阻力特性、湍流阻力特性和矩形窄通道单相流摩擦阻力进行了实验研究，得出了摇摆状态层流瞬时摩擦阻力系数的计算公式及摩擦系数随振动参数的变化规律。谭思超等[13]对摇摆运动下窄矩形通道低流速单相瞬变流动时均阻力特性进行了实验研究，发现先求解阻力系数和先求解压差再求解阻力系数的结果不同，分别能够代表时均黏性耗散和时均摩擦阻力压降。Yu等[14]研究了振动对自然循环流动特性的影响，提出了能准确预测单相自然循环流动流量波动特性的模型。谢清清等[15]在不同摇摆周期和角度下对光滑窄矩形通道内单相流动阻力特性进行了实验研究，发现摩擦阻力系数具有周期性波动特性，摩擦阻力系数与雷诺数呈反比，与摇摆角加速度呈正比。

目前非稳态流动阻力的研究主要集中在摇摆运动方面，尚未有关于起伏振动单相流动阻力的相关研究。本文通过对不同流动和振动工况下单相水的流动阻力特性进行分析，将传统摩擦压降和振动引起的附加压降定义为起伏振动下的摩擦压降，得出起伏振动状态下单相水的流动阻力变化规律，为起伏振动下单相流动阻力的计算提供指导。

1 实验装置和方法

本文实验采用电磁式起伏振动台，在控制器的作用下产生指定类型的起伏振动。实验系统如图1所示。

图1 实验系统Fig.1 Experimental system

振动台在控制器的控制下做正弦起伏振动，其运动规律为：

y=Asin(2πft)

(1)

v=2πfAcos(2πft)

(2)

a=-4π2f2Asin(2πft)

(3)

式中：y为瞬时位移，m；A为振幅，m；f为振动频率，Hz；t为时间，s；v为瞬时振动速度，m/s；a为瞬时振动加速度，m/s2。

实验段为光滑有机玻璃圆管，管道内径分别为15、20和30 mm，通过支架固定在振动台上，实验段倾角θ分别为10°、24°和45°。实验段上开有两个测压孔，间隔为0.8 m，用于流动压力的取样。流动压降采用差压传感器测量，量程为0～25 kPa，精度为0.2级。振动台的加速度用加速度传感器进行测量，量程为0～30 m/s2，精度为0.5级。管道流量采用电磁流量计测量，量程为0～10 m3/h，精度0.5级。振动参数分别为：频率2、5和8 Hz，振幅2、5和10 mm。

2 实验数据处理

文献[2]指出，海洋条件下流动受到附加力的作用会产生附加压降，因此起伏振动倾斜管单相水的压降主要由摩擦压降Δpf、重位压降Δpg和附加压降Δpadd组成，即：

Δp=Δpf+Δpg+Δpadd

(4)

对于倾斜管，两个引压管之间存在液柱差，该部分压力差值与实验段中水的重位压降相互抵消。则：

Δp=Δpf+Δpadd

(5)

以往研究中均根据文献[2]的公式计算附加压降或将引压管中的附加压降与实验段中的附加压降抵消，不仅增加了实验误差，而且使得计算过程复杂化。本文将振动附加力当作摩擦力的一部分，把摩擦压降和附加压降合并，称为起伏振动摩擦压降Δpfv，即：

Δp=Δpfv

(6)

振动摩擦阻力系数λv仍根据稳定状态下的Dancy-Weisbach公式计算：

(7)

式中：D为管道直径，m；ρ为流体密度，kg/m3；L为取压孔间距，m；u为管道截面平均流速，m/s。

3 实验结果分析

3.1 起伏振动对摩擦压降的影响

文献[10]将附加压降进行抵消处理，结果表明摇摆运动引起摩擦压降的波动，但摇摆工况的改变对平均摩擦阻力没有明显影响。文献[16]没有单独考虑附加压降，计算了起伏振动时液氢流动的平均摩擦压降，发现振动会导致压降的增大。但其中涉及相变问题，作者将压降的增大归因于管内气相的增加。本实验得出的D=15 mm、u=1.38 m/s、f=5 Hz、A=5 mm时起伏振动和稳定状态下的摩擦压降如图2所示。结果表明，起伏振动摩擦压降表现出明显的类似正弦函数波动，波动范围为平均值的22.8%～204.8%。此外，起伏振动摩擦压降平均值为3.42 kPa，稳定状态下摩擦压降为0.69 kPa，起伏振动摩擦压降平均值远大于稳定状态，这说明起伏振动显著增加单相流动的沿程损失。这是因为起伏振动引起的附加力增大了管内流体微团间和管内流体与壁面间的碰撞，导致能量损失增大。

图2说明起伏振动导致单相流动具有不稳定性，通过对摩擦压降进行傅里叶分析得到起伏振动和稳定状态下摩擦压降的波动频率，如图3所示。由图3可知，在起伏振动状态下摩擦压降波动有显著的主频分量，其他谐波分量可忽略不计，这说明起伏振动状态下摩擦压降表现出规律的周期性波动，而稳定状态下的摩擦压降不存在波动周期，此时摩擦压降保持稳定。摩擦压降波动中振动频率分量比重最大，即摩擦压降的波动频率与起伏振动频率一致。

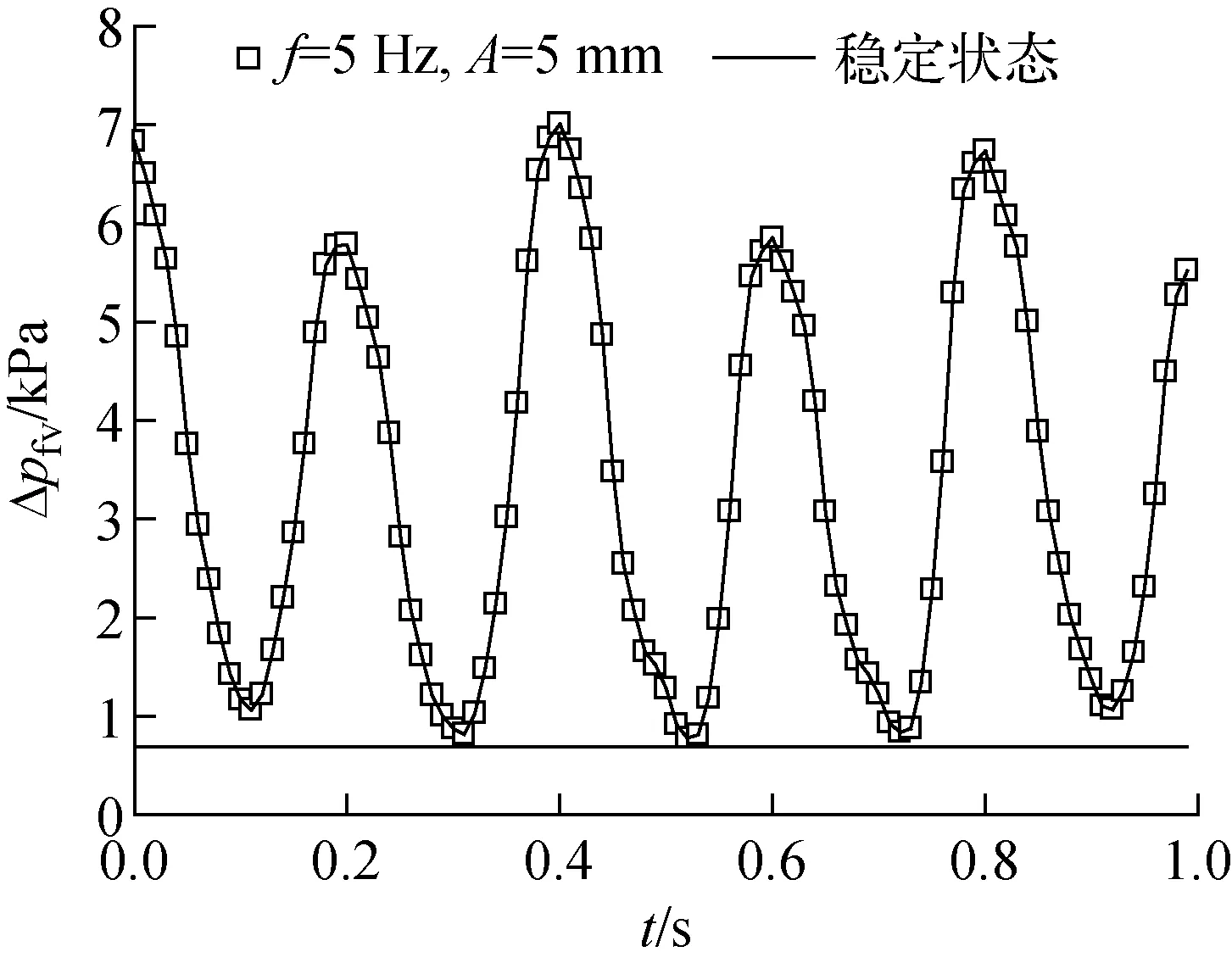
图2 稳定状态和起伏振动状态的摩擦压降对比Fig.2 Comparison of friction pressure drop between steady and undulating vibration conditions

图4示出f=5 Hz、A=5 mm时摩擦压降随加速度的波动。由于实验采用离心泵提供水头，结合文献[6]可得出采用离心泵提供水头时瞬时流量不随振动呈现周期性变化，因此摩擦压降的周期性变化主要由振动引起的周期性作用力导致。将1个振动周期分为4个阶段，管道的运动及管内流体微元受力如图5所示。在1阶段，管道从平衡位置向下运动，管内流体微元受力为向下的重力g和向上的附加力Fa的合力，随振动加速度的增大，Fa逐渐增大，流体微元与管壁作用力减小，摩擦压降减小，在1阶段结束时摩擦压降达到最小值。在2阶段，管道从下限位置向上运动，管内流体微元受力为向下的重力g和向上的附加力Fa的合力，随振动加速度的减小，Fa逐渐减小，流体微元与管壁作用力增大，摩擦压降增大。在3阶段，管道从平衡位置向上运动，管内流体微元受力为向下的重力g和向下的附加力Fa的合力，随振动加速度的增大，Fa逐渐增大，流体微元与管壁作用力增大，摩擦压降增大，在3阶段结束时摩擦压降达到最大值。在4阶段，管道从上限位置向下运动，管内流体微元受力为向下的重力g和向下的附加力Fa的合力，随振动加速度的减小，Fa逐渐减小，流体微元与管壁作用力减小，摩擦压降减小。

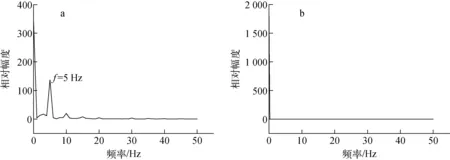
a——起伏振动状态，f=5 Hz，A=5 mm；b——稳定状态图3 稳定状态和起伏振动状态的摩擦压降波动频率Fig.3 Friction pressure drop fluctuation frequency of steady and undulating vibration conditions

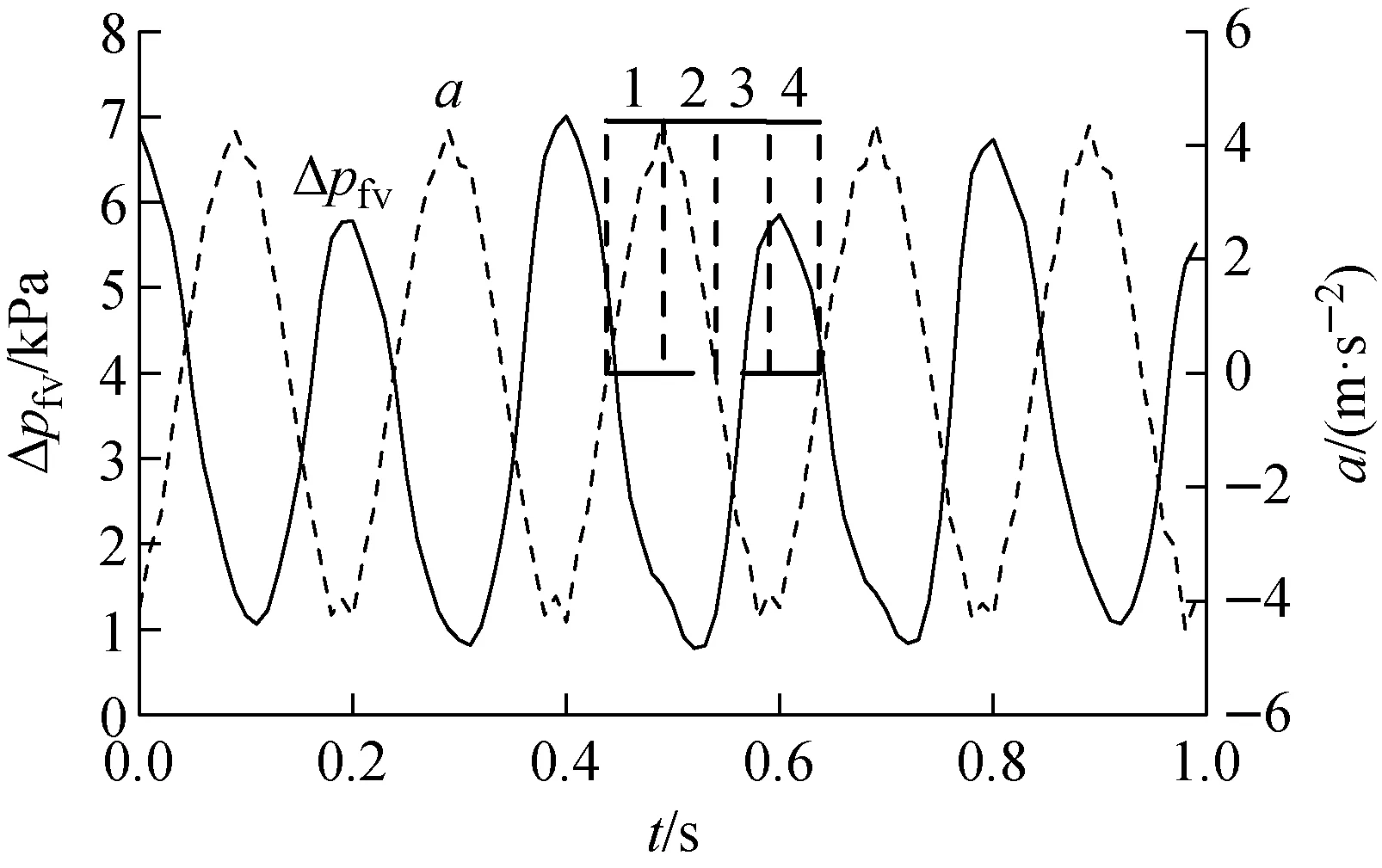
图4 起伏振动下摩擦压降与振动加速度的关系Fig.4 Relationship between friction pressure drop and vibration acceleration under undulating vibration

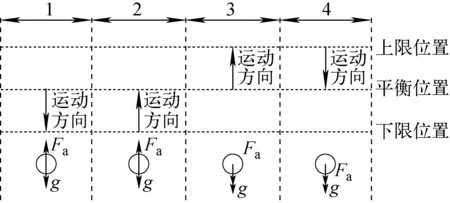
图5 f=5 Hz时管道运动及管内流体微元受力分析Fig.5 Analysis of pipeline movement and micro-element stress of fluid in pipe with f=5 Hz

3.2 管径对流动阻力特性的影响

f=5 Hz、A=5 mm、Re=27 900、D分别为15、20、25和30 mm时单相水的振动摩擦阻力系数波动如图6所示。由图6可知，随管径的变化，振动摩擦阻力系数λv的平均值有显著变化。当D从15 mm增加至20 mm时，λv的平均值从0.028增至0.077，瞬时值相对于平均值的波动范围无明显变化。这是因为随管径的增大，管内水的波动程度增大，进而增大了能量损失，摩擦阻力系数增大。当D从20 mm增加至30 mm时，λv的平均值从0.077降至0.058，且当D=30 mm时λv的峰值表现为一高一低地变化，瞬时值相对于平均值的波动范围有所减小。这是因为随管径的继续增大，振动对流动的影响相对减小，导致λv的波动范围和平均值有所减小。

图6 不同管径下振动摩擦阻力系数的波动Fig.6 Fluctuation of vibration frictional resistance coefficient under different pipe diameters

3.3 倾角对流动阻力特性的影响

f=5 Hz、A=5 mm、D=15 mm、Re=35 160时不同倾角(θ)下振动摩擦阻力系数的变化如图7所示。由图7可知：当θ从10°增至24°时，λv平均值从0.042降至0.023；当θ从24°增至45°时，λv平均值从0.023降至0.02。这说明λv平均值随倾角的增大而减小，随倾角的增大，λv平均值的减小幅度降低。这是因为随倾角的增大，振动附加力在垂直于壁面方向上的分力减小，对流动的影响削弱，使得振动摩擦阻力系数减小。

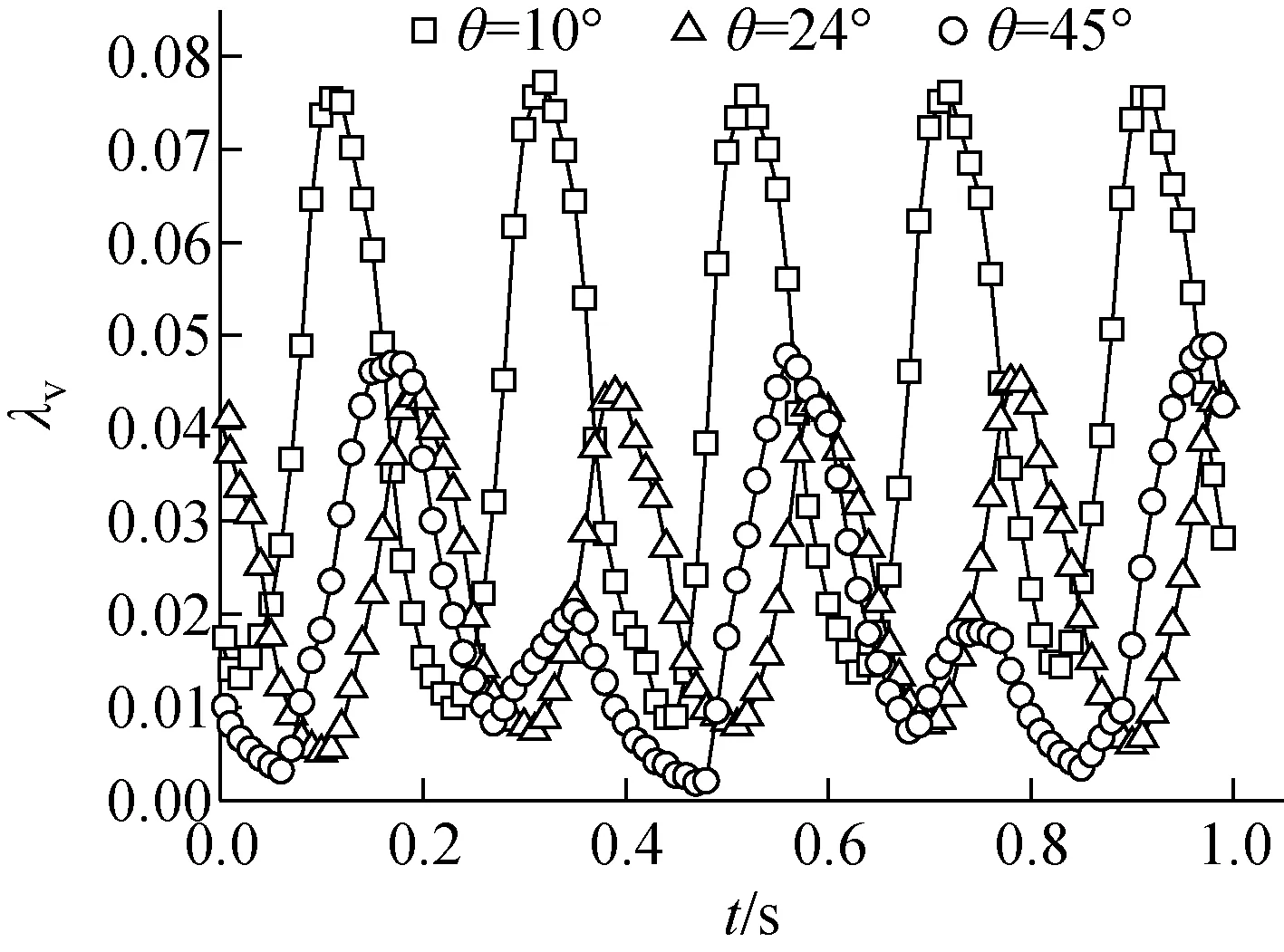
图7 不同倾角下振动摩擦阻力系数的波动Fig.7 Fluctuation of vibration frictional resistance coefficient under different angles

3.4 雷诺数对流动阻力特性的影响

f=5 Hz、A=5 mm、D=15 mm时不同Re下的振动摩擦阻力系数的变化如图8所示。由图8可知：Re=20 600时，λv平均值为0.067；Re=35 160时，λv平均值为0.027。振动摩擦阻力系数与Re呈反比，这与稳定状态下的摩擦阻力系数变化规律一致。此外，随Re的变化，瞬时振动摩擦阻力系数的波动情况也有所不同。Re=20 600时，λv的波动范围为平均值的22.8%～204.7%；Re=35 160时，λv的波动范围为平均值的19.2%～183.6%。这说明随Re的增加，λv的波动范围减小。产生这种现象的原因是相同振动下，随Re的增加，振动附加力对流动的影响减小，进而使得λv的波动范围减小。

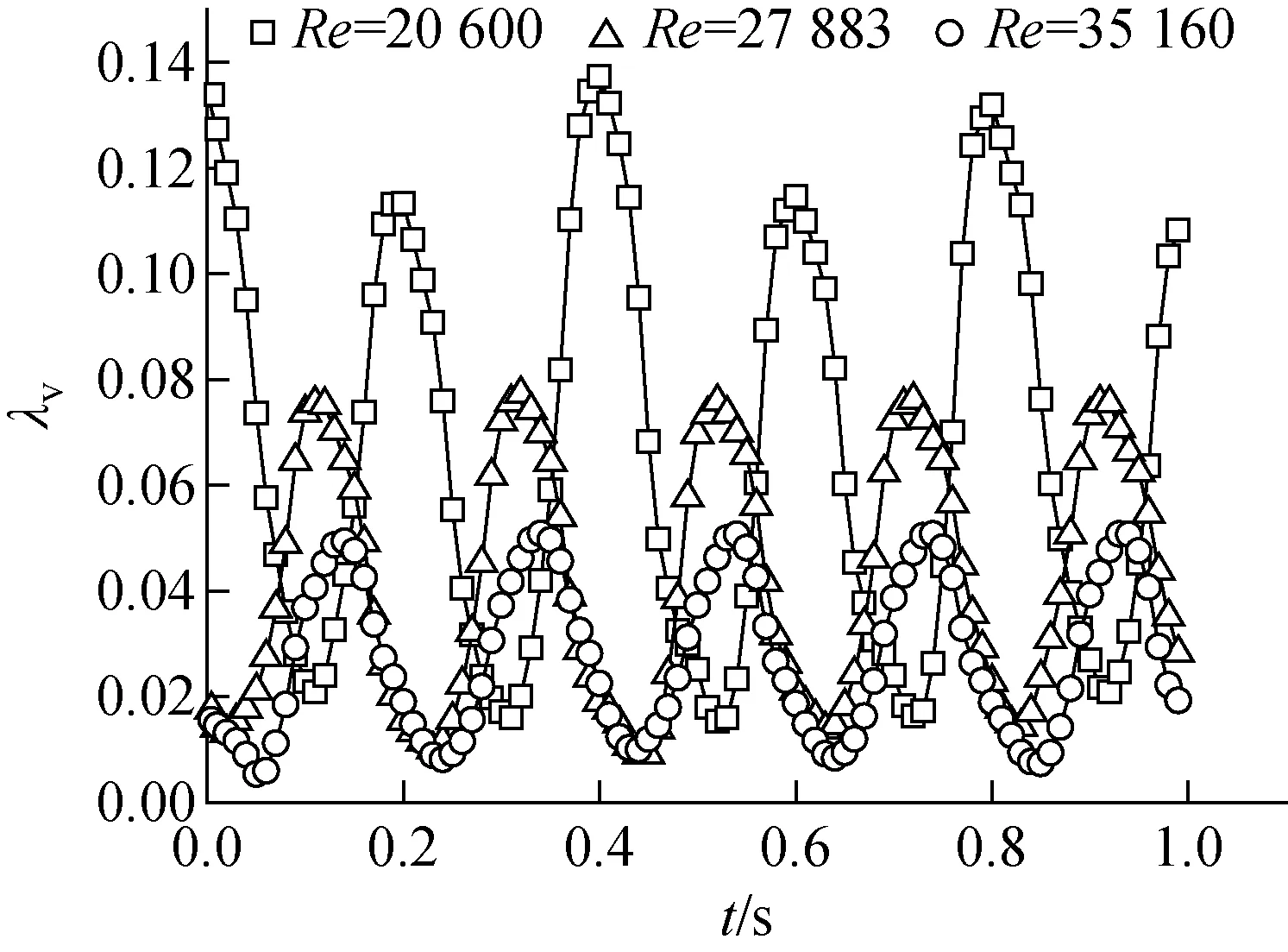
图8 不同Re下振动摩擦阻力系数的波动Fig.8 Fluctuation of vibration frictional resistance coefficient at different Re

3.5 起伏振动频率对流动阻力特性的影响

由式(3)可知，振动加速度与振动频率的平方呈正比，振动频率的改变会严重影响振动附加力，进而改变振动摩擦阻力系数。D=20 mm、Re=27 826、A=5 mm时不同振动频率下振动摩擦阻力系数的变化如图9所示。由图9可知，相同振幅下振动频率的改变会引起振动摩擦阻力系数的平均值和波动规律的变化。当f由2 Hz增至5 Hz，λv的平均值由0.029增至0.076，λv的波动范围由19.5%～207.9%变化至20.7%～183.4%；当f由5 Hz增至8 Hz，λv的平均值由0.076降至0.034，λv的波动范围由20.7%～183.4%变化至4.1%～304.1%。

这种变化产生的原因可用图5的受力分析解释。当振动频率较低时，振动附加力较小，此时水和管道同步振动。随振动频率的增大，水的纵向运动加剧，能量损失增大，导致摩擦压降的增大。同时随振动频率的增大，水的运动方向改变速度加快，同一方向上的力持续作用时间减小，导致振动摩擦压降的波动幅度减小。当振动频率较大时，振动附加力较大，此时水和管道的运动不同步。随振动频率的增大，水在振动附加力和惯性的作用下会持续一段时间集中于管道中间，水和管道壁面的作用力很小，振动摩擦压降会在低位保持一定的时间，如图9所示。当水在管道中间的状态结束后，水的运动和管道运动叠加，导致摩擦压降迅速增大到最大值。

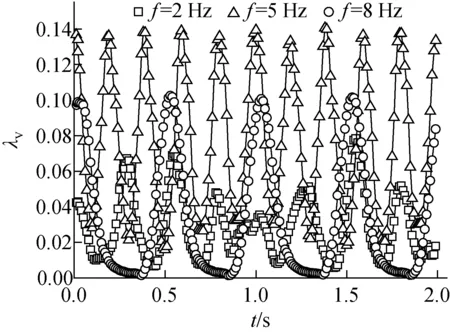
图9 不同振动频率下振动摩擦阻力系数的波动Fig.9 Fluctuation of vibration frictional resistance coefficient at different vibration frequencies

3.6 振幅对流动阻力特性的影响

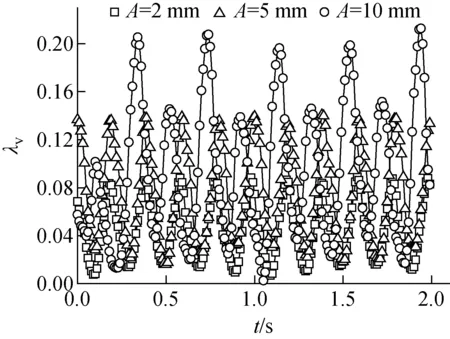
图10 不同振幅下振动摩擦阻力系数的波动Fig.10 Fluctuation of vibration frictional resistance coefficient at different amplitudes

振幅的改变同样会引起振动附加力的变化，进而改变振动摩擦阻力。D=20 mm、Re=27 826、f=5 Hz时不同振幅下振动摩擦阻力系数的变化如图10所示。由图10可知，A从2 mm增至10 mm时，λv的平均值从0.045增至0.092。这是因为振动附加力与振幅的一次方呈正比，随振幅的增大，振动加速度增大，但并不能引起水与管道的相对运动状态的变化，仅使得管内水与壁面的作用力增大，导致振动摩擦阻力系数的增大。

4 起伏振动状态下单相水摩擦阻力系数计算

由以上分析可看出，起伏振动状态下的振动摩擦阻力系数周期性波动比较明显，不能用稳定状态下的计算模型计算，需要提出适用于起伏振动状态的振动摩擦阻力系数计算公式。通过以上分析可得出振动摩擦阻力系数主要与摇摆状态(a，v)、Re和当量直径有关，根据量纲分析中的π定理可导出振动摩擦阻力系数的表达式。起伏振动状态下单相流振动摩擦阻力特性物理方程为：

F(Δpfv,μ,ε,a,v,D,L,ρ,u,θ)=0

(8)

式中：μ为流体的动力黏度，N·s/m2；ε为管道粗糙度，m。

本研究试验管段为光滑有机玻璃管，忽略粗糙度的影响，则振动摩擦压降为：

(9)

起伏振动状态下的振动摩擦阻力系数可表示为：

(10)

通过对影响因素和大量数据分析，最终将振动摩擦阻力系数写为如下形式：

(11)

为了分析振动对流动特性的影响，定义振动雷诺数Rev如下：

(12)

式中，vv为振动平均速度，由下式计算：

vv=4vmf

(13)

式中，vm为起伏振动速度最大值。

通过对大量实验数据进行拟合，得到式(11)中c1、c2和c3的关系式为：

(14)

本文得出的起伏振动状态下振动摩擦阻力系数计算值和实验值的对比如图11所示。从图11可明显看出，该关系式能较准确地计算振动摩擦阻力系数。在峰值和谷值由于波动较剧烈，实验测量值随机性较大，因此关系式误差较大，在中间位置的拟合误差均在10%以内。该关系式的适用范围为f<8 Hz、A<10 mm、4 6878 Hz的情况，并且在实际应用中几乎不存在这种高频率振动，因此水和管道振动异步情况下的振动摩擦阻力系数计算模型还有待进一步研究。该关系式的适用范围有限，主要为非稳定状态下振动摩擦阻力的计算提供一种分析思路。

a——D=15 mm，Re=20 645，f=2 Hz，A=5 mm；b——D=15 mm，Re=20 645，f=2 Hz，A=10 mm图11 振动摩擦阻力系数计算值和实验值的比较Fig.11 Comparison of calculated value and experimental valueof vibration frictional resistance coefficient