基于改进Gauss-Hermite方法的在线多普勒展宽方法研究

刘仕倡，王 侃，陈义学

(1.华北电力大学 核科学与工程学院，北京 102206；2.清华大学 工程物理系，北京 100084)

蒙特卡罗方法可根据原子核的反应截面来随机模拟中子与不同核素相互作用时的反应概率。材料温度将影响靶核热运动，从而对反应截面产生影响，这就是所谓的多普勒效应。在核反应堆的高保真模拟中，燃料和慢化剂有非常精细的温度变化和分布。因此，对于不同温度下的截面必须采用特殊处理。

传统方法是预先产生不同温度点的截面用于插值。基于线性插值点数据卷积的Sigma1方法是预处理工具中最常用的方法，如NJOY[1]。然而，当温度点数较多时，预生成的方法会带来内存占用方面的问题。近年来，为减少内存的占用，在多物理耦合计算中提出了几种在线温度截面处理技术。MCNP6[2]提出了基于级数展开的温度拟合方法。Becker等[3]提出了利用随机抽样算法计算有效多普勒展宽截面的方法。为提高随机抽样的效率，Serpent程序还提出了另一种拒绝抽样算法(TMS方法)[4]。在OpenMC[5]中使用了另一种称为多极点(multipole)表示的方法。Dean等[6]提出了应用Gauss-Hermite积分来计算多普勒展宽方程的方法。

然而，现有的方法均有其局限性。例如，MCNP6中的温度拟合方法依赖于预先生成的系数。OpenMC中的多极点表示方法依赖于预先生成的多极点数据。拒绝抽样方法不能使用径迹长度估计器，这将限制该方法的应用。其他方法如Sigma1法和传统的Gauss-Hermite法存在效率低的问题。因此，有必要提出一种新的在线多普勒展宽方法，该方法不需进行温度拟合和多极点数据生成等额外的处理，从而提高计算精度和效率。

本文提出一种新的Gauss-Hermite求积方法，并在蒙特卡罗程序RMC[7]中实现，以提高传统Gauss-Hermite求积方法的效率。

1 基于积分的多普勒展宽方法

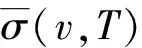
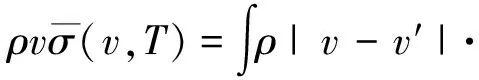
σ(|v-v′|,0)P(v′,T)dv′

(1)

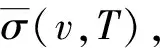
1.1 Sigma1方法

Sigma1方法是利用点截面的线性化特性进行卷积，将式(1)转化为式(2)：

[e-α(v-V)2-e-α(v+V)2]dV

(2)

α=M/2kT

(3)

式中，v和V分别为中子速度和中子相对于靶核的速度。为简化式(2)，定义了如下变量：

x2=αV2

(4)

y2=αv2

(5)

将式(2)转化为：

(6)

再定义：

(7)

式(6)可拆分为两部分：

式(6)最终可转化为一系列Hn的叠加，该函数定义如下：

(8)

式中，n为次数。

在实际应用中，式(8)的求解无论采用误差余函数还是Taylor展开均非常耗时。

1.2 Gauss-Hermite正交基函数法

Gauss-Hermite正交基函数定义为：

(9)

为使式(7)形式类似式(9)的形式，定义变量z=x-y，将式(7)写为：

(z+y)2e-z2dz

(10)

式中：z为求积组的取值点；n为求积组取值点的数目，如图1所示；y代表中子速度，x=z+y代表相对速度。对于式(10)，注意到指数项的存在，z的取值范围为-4≤z≤4即可。需注意的是，式(10)的积分下界为负无穷。因此当y>4时，式(10)可用Gauss-Hermite多项式表示，而y<4时则不能。因此，在应用Gauss-Hermite方法时，必须考虑适用范围为y>4。y<4时将采用高斯-勒让德求积组或Sigma1算法。在Romano的实现[8]中也采用了相同的处理方法。在Romano的实现中，使用了16点正交求积组。

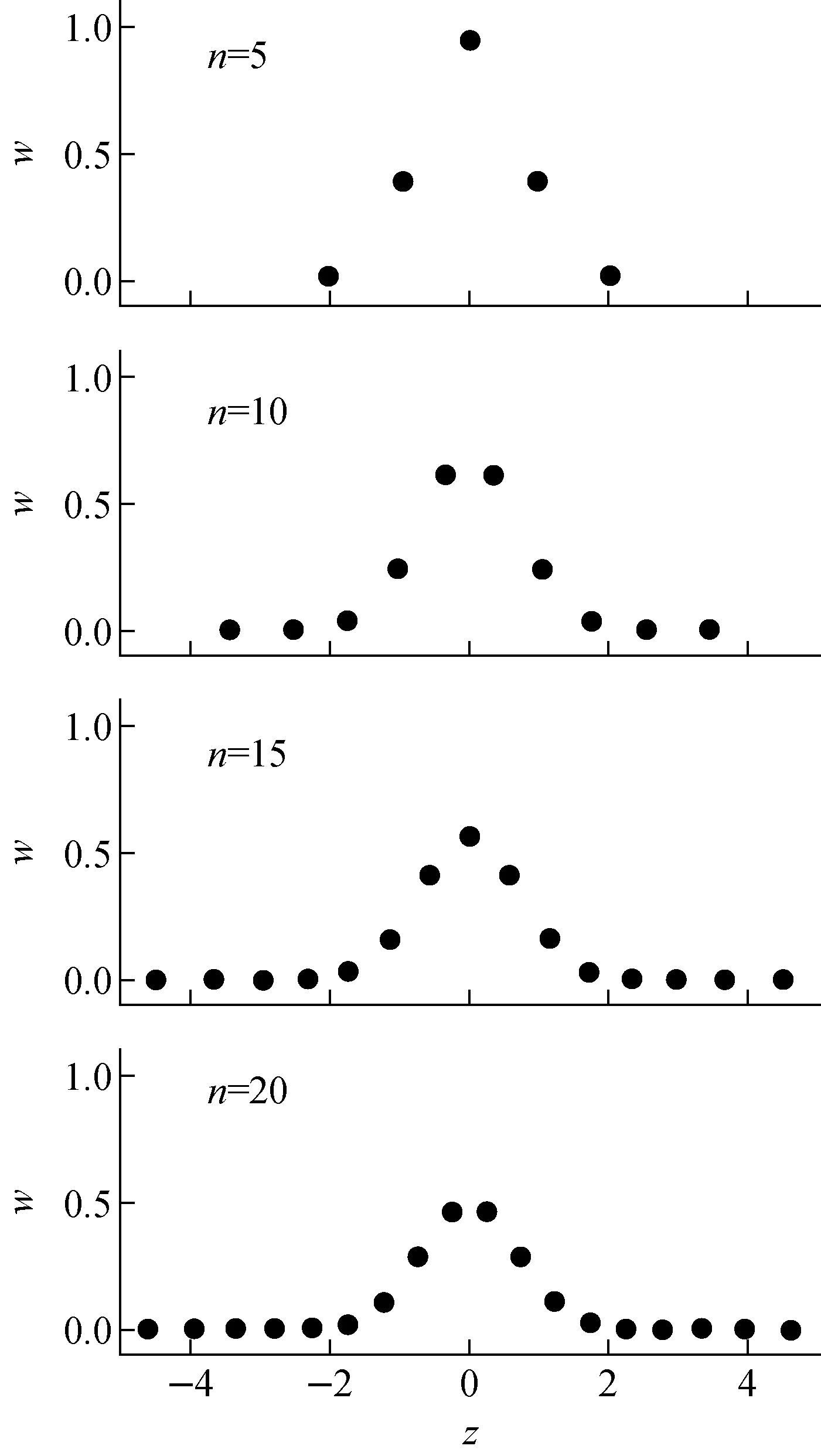
图1 Gauss-Hermite多项式求积组Fig.1 Diagram of Gauss-Hermite quadrature

然而，退回到高斯-勒让德求积组或Sigma1算法将降低Gauss-Hermite方法的效率。此外，Gauss-Hermite方法在能量网格中搜索相对能量x，以及插值相应的截面时效率较低。

2 改进Gauss-Hermite方法

针对传统Gauss-Hermite方法存在的问题，提出了改进Gauss-Hermite方法。解决这些问题的一些关键技术如下。

2.1 低能段的修正

众所周知，低能段截面是相对比较光滑的，如图2所示。一般地，低能散射截面变化很小，接近1个常数；而低能吸收、裂变截面服从1/v率。因此，由式(1)可知，经过多普勒展宽后，吸收截面保持不变，而散射截面应乘以修正项，如式(11)所示。

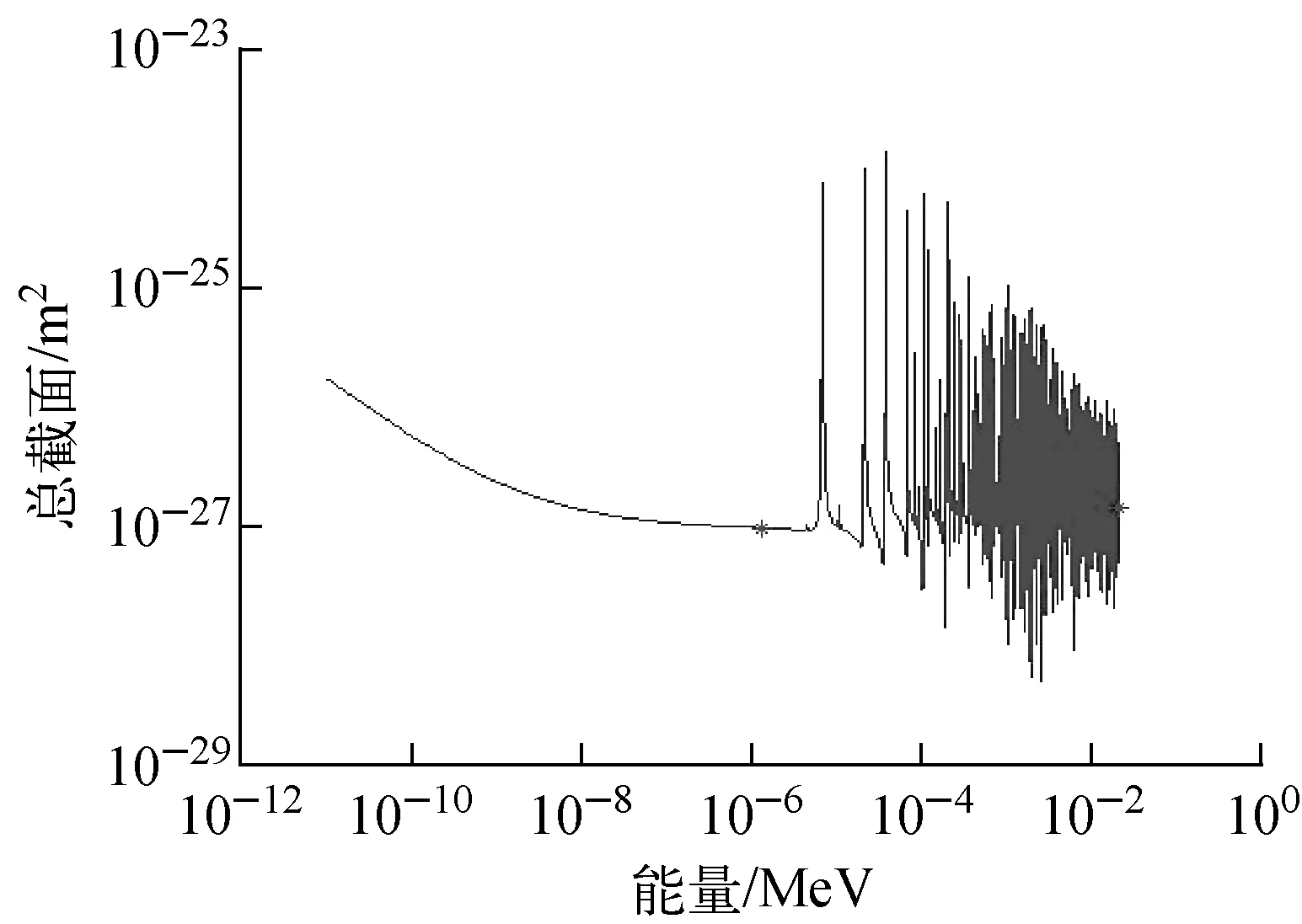
图2 900 K时238U总截面Fig.2 Total cross section of 238U at 900 K

(11)

erf是误差函数，并且：

(12)

式中，n为核素。

通过上述处理，对于低能光滑段，利用式(11)修正散射截面时，不使用Gauss-Hermite方法，这可减少Gauss-Hermite方法的使用频率，代之以计算成本较低的修正项。从而避免了Gauss-Hermite方法在低能段y<4不适用的问题。

低能区与共振能区的分界点很重要，必须采用合理的方法将低能区与共振能区划分开。

2.2 共振段的开始和结束能量

如上所述，低能区与共振能区的分界点可称为共振的起始能量或低能光滑段的结束点。低能光滑段的结束点可根据每个核素所在的最大温度下多普勒展宽的作用范围来确定，从而得到低能光滑段的结束点。对于某个中子能量点，根据中子与靶核之间的最大相对能量和最小相对能量，可找到上界和下界。然后计算出上、下界的差值，将低能光滑段结束点作为共振的起始能量，如图3所示。

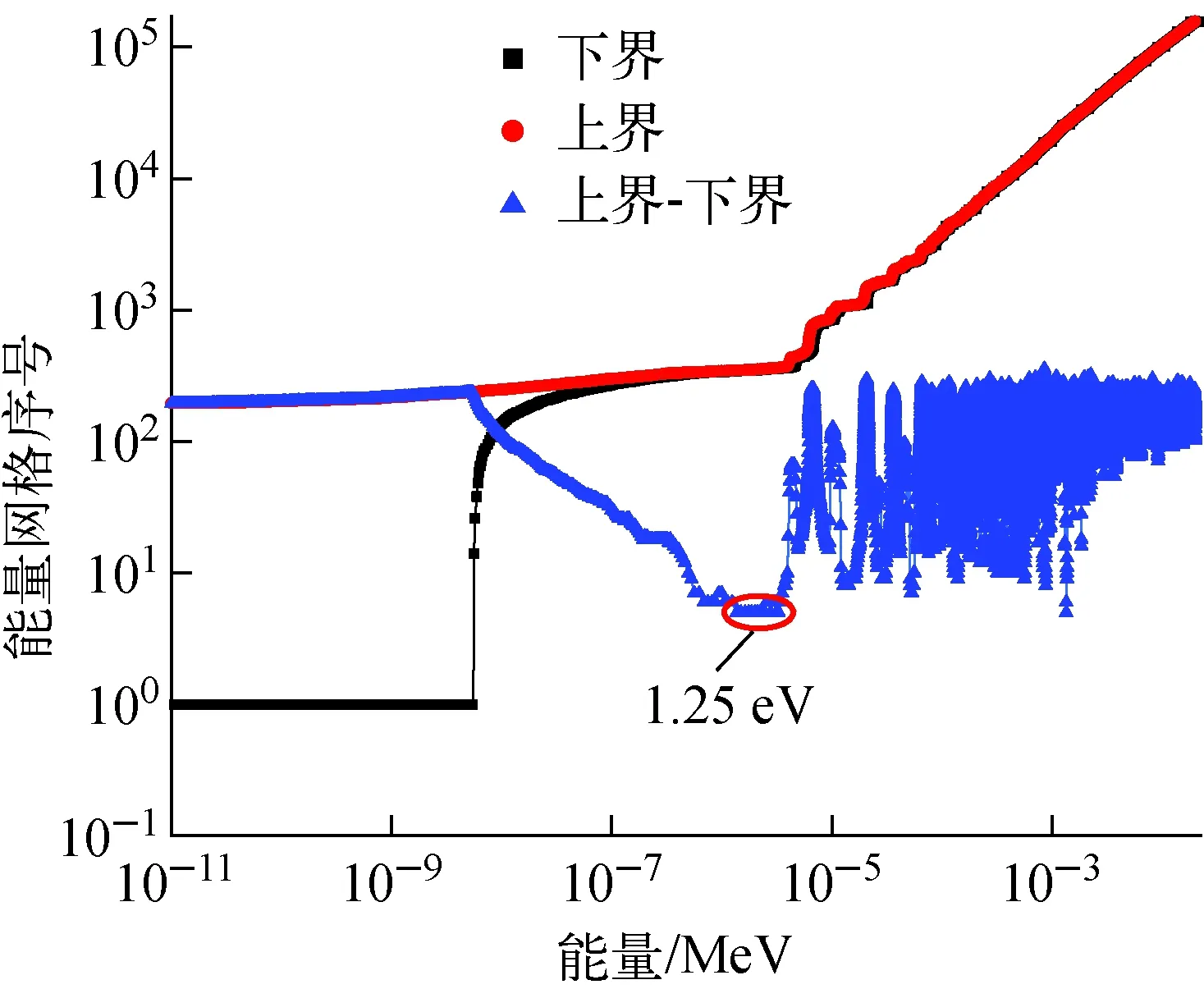
图3 低能光滑段的结束点Fig.3 End point of low energy smooth segmen

利用上述算法，图3中低能光滑段结束点为1.25 eV。而从图2可看出在4.41 eV附近有1个很小的共振峰。可见，提出的上界-下界算法可有效地找出低能光滑段结束点。

共振段结束点的查找方法与NJOY的处理一致，即可分辨共振区的上界、阈能反应对应的最小能量以及1 MeV三者的最小能量。

2.3 多普勒展宽哈希表

另一个重要的改进是多普勒展宽哈希表的使用。在Gauss-Hermite方法中，寻找相对能量的能量网格序号非常耗时。RMC中采用了哈希表方法，来加速能量网格查找的速度[9]。例如，当前中子能量为E，哈希表先根据E找到对应的能量分箱i，然后再在能量分箱i中使用二分法查找能量E对应的网格序号。

当哈希表确定了能量分箱i后，可得到分箱i的能量上、下界Eupper和Elower，而根据Eupper和靶核速度可得到最大相对能量Emax，根据Elower和靶核速度可得到最小相对能量Emin。当中子能量在哈希表的分箱i内时，多普勒展宽后的相对能量将位于多普勒展宽哈希表的分箱i内，如图4所示。

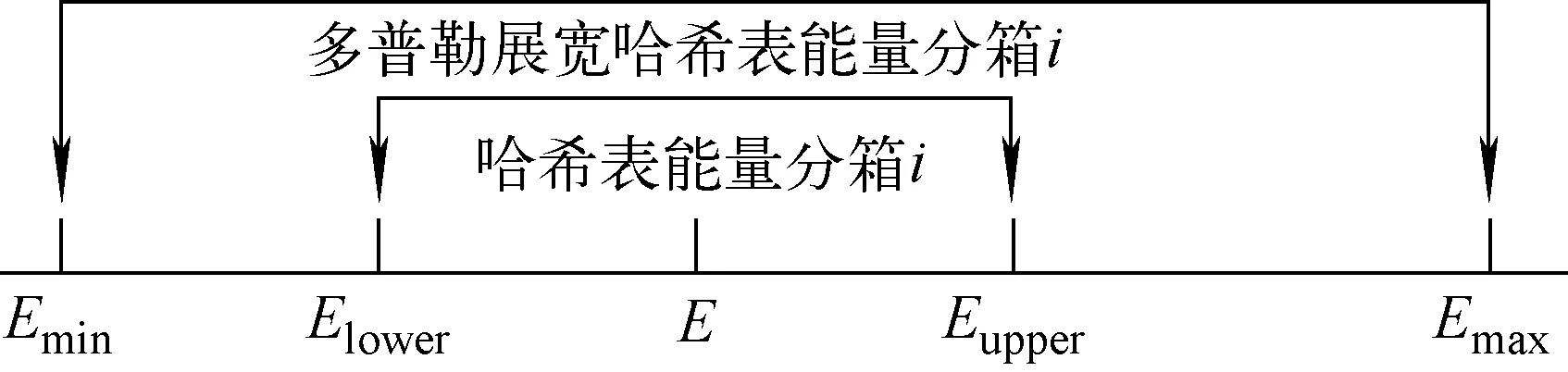
图4 多普勒展宽哈希表Fig.4 Diagram of Doppler broadening Hash map

3 结果与分析

采用典型17×17压水堆组件模型，如图5所示，组件模型参数列于表1。对多普勒展宽的精度和效率进行了测试。在每个栅元中均有燃料、气隙(16O)、轻水(1H、16O)。燃料温度为900 K，其他材料温度为600 K。蒙特卡罗计算中，每代使用100 000个中子，共1 000代，其中300个非活跃代。选取了采用基于ENDF/B-Ⅶ.0的精确温度库的RMC结果作为参考。

图5 典型压水堆组件模型Fig.5 Typical PWR assembly model

参数数值燃料密度,g/cm310.196 燃料富集度,%3燃料芯块半径,cm0.409 6燃料包壳外径,cm0.475 0栅距,cm1.26冷却剂密度,g/cm31.0

改进Gauss-Hermite方法采用300 K的ACE库作为基础数据库。在输运及燃耗计算中，均采用了哈希表加速，并对燃料棒中的中子能谱进行统计。

3.1 输运计算

对于输运计算，燃料中仅有235U、238U、16O。表2对kinf进行了比较。可看出传统Gauss-Hermite方法和改进Gauss-Hermite方法与精确库的差别均在1倍标准偏差左右。传统Gauss-Hermite方法的计算时间是参考值的9.3倍，而改进Gauss-Hermite方法时间仅增加了10%。

表2 压水堆组件算例的kinf和计算时间Table 2 kinf and calculation time of PWR assembly case

图6比较了3种方法的中子能谱，可看出传统和改进Gauss-Hermite方法的能谱均与参考值很接近。大部分相对误差在5%以内。较大的相对误差仅出现在通量本身很小的能量点。

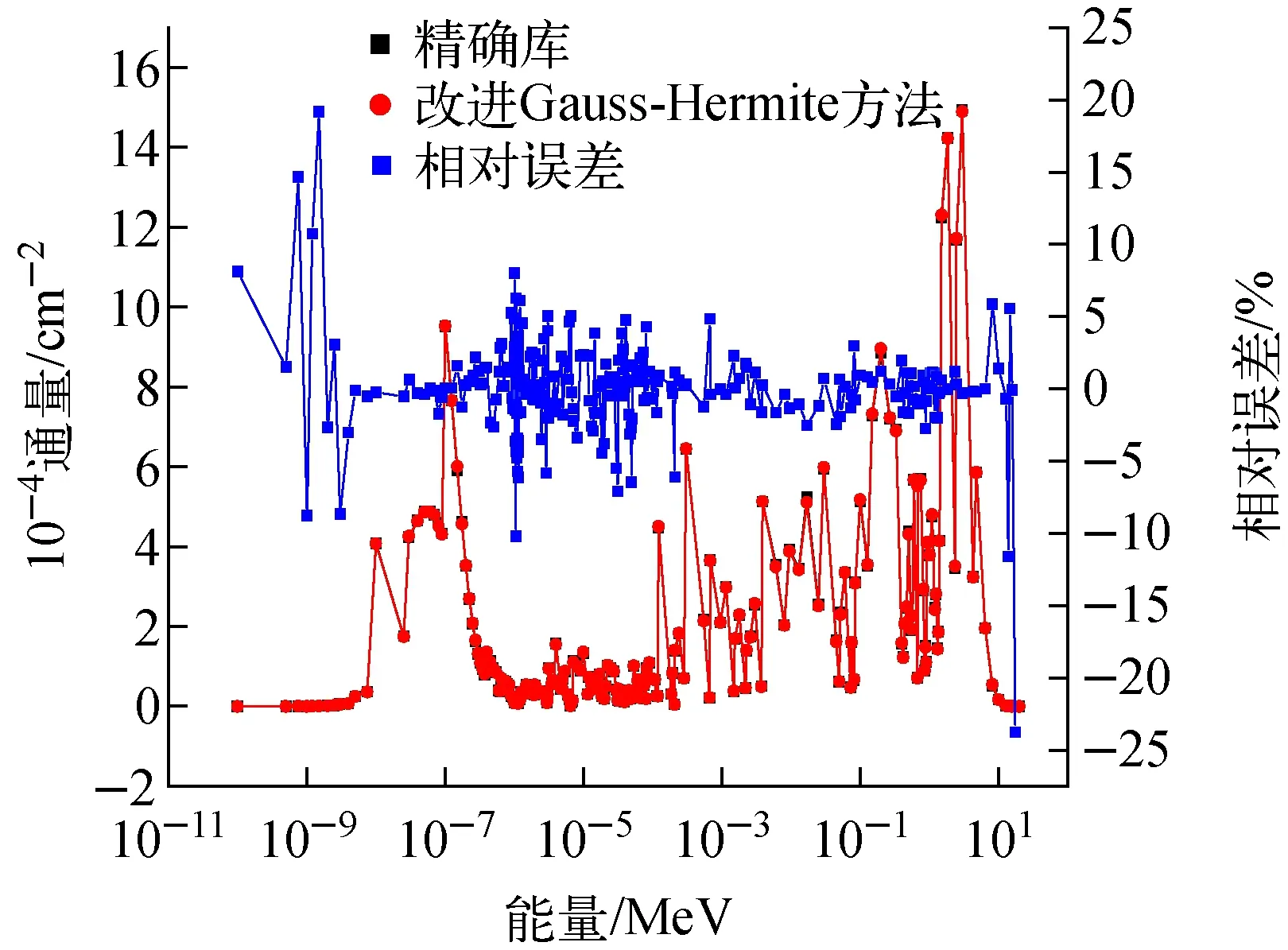
图6 压水堆组件算例的能谱相对误差Fig.6 Relative error of energy sprectrum for PWR assembly case

3.2 输运-燃耗耦合计算

第2个算例为燃耗后(58.065 MW·d/kg(HM))的PWR组件，燃料中共134种核素。此次计算还增加了燃料中核素的燃耗相关单群截面统计，因此相当于输运-燃耗耦合计算进行到58.065 MW·d/kg(HM)的一步输运计算。

从表3可看出，改进Gauss-Hermite方法的时间增加了29%，而kinf仅相差6.5 pcm。而传统Gauss-Hermite方法的时间为精确库的3.45倍。改进Gauss-Hermite方法在带燃耗相关单群截面统计的输运计算的效率较TMS方法(1.98倍)和OpenMC的Multipole方法(1.59倍)的高，因此更适合应用于输运-燃耗耦合计算。

表3 带单群截面统计的燃耗后PWR组件算例的kinf和计算时间Table 3 kinf and calculation time of burned PWR assembly case with one group cross section

4 结论

本文提出了一种改进Gauss-Hermite方法，并在蒙特卡罗程序RMC中进行了编程实现。压水堆燃料组件算例的输运和燃耗计算结果表明，改进Gauss-Hermite方法精度与传统Gauss-Hermite方法相当，而且可大幅提高计算效率，特别是输运-燃耗耦合计算的效率。该方法简洁而直接，避免了额外的预处理过程，为在线多普勒展宽提供了一种新的有效方法。因此，该方法能适用于各种蒙特卡罗粒子输运程序，具有良好的应用前景，为高保真多物理耦合计算奠定基础。