基于多孔介质理论的油井水泥石破坏准则
2020-05-07丁嘉迪沈吉云张硕纪宏飞王琳琳
丁嘉迪,沈吉云,张硕,,纪宏飞,王琳琳
(1.中海油服油田化学研究院,河北三河 065201;2.中国石油集团工程技术研究院有限公司,北京 100101;3.中国石油大学(北京),北京 100083)
0 引言
固井水泥浆凝固后形成的水泥环应该对地层进行有效的层间封固,并为套管提供保护和支撑。其能否保持密封完整性,对后续钻井及油气开采至关重要。水泥环密封失效将引起地层流体泄漏,造成油气资源的浪费,甚至导致全井报废。2010 年BP公司(BP Amoco 英国石油公司)在墨西哥湾的钻井平台发生事故就与水泥环密封失效有关[1]。
随着国内外勘探开发逐渐转向对深层、低渗透、非常规以及海洋油气的开采利用,长水平井、低压易漏井、非常规油气井、储气库井等复杂井日益增加,同时安全环保的要求日益严格,固井后水泥环的密封性面临许多新的挑战[2],深井超深井由于井深较深,井筒内流体密度变化、生产过程高温油气上升等均会导致井筒温度、压力大幅变化,易出现环空带压、井口抬升等问题[3-4]。页岩气[5]、致密油气井普遍采用水力压裂的开发方式,压裂压力高、井筒压力反复变化,水泥环容易产生密封失效。对实际工况下水泥石力学行为进行准确描述是计算水泥环在复杂工况下的应力分布、预测完整性失效的前提。
水泥石的组成包括固体水泥石骨架和孔隙内流体,通过微观扫描电镜[6]观测验证水泥石存在孔隙结构。油井井筒所处的深层地下往往为高水压环境,水泥石凝固后其内部孔隙经常处于饱水带压力的情况,其力学性能较常压下的水泥石有很大不同。而考虑有孔隙流体的水泥石实际承受的压力包括水泥石在井下的孔压、水泥石自重以及围岩的压力。紧挨围岩的水泥石内流体压力与地层流体压力保持一致,水泥石骨架承受的载荷实际上是有效应力。目前国内固井的一些固井水泥石力学性能评价,只将水泥石考虑成均质固体[2-3],清华大学高岳[7]以及中国石油大学(北京)王琳琳、中石油工程技术研究院[8-9]已经开始将多孔介质理论应用于油井或者页岩领域进行力学分析。
国外研究中,Terzaghi[10]最早于1923 年提出了有效应力原理,这是最早考虑了孔隙流体对材料影响的理论,这一理论在1936 年由Rendulic[11]从一维推广到了三维。Biot[12]在1940 年针对多孔介质进行进一步研究,发现孔隙压力对有效应力的影响存在一个系数,被称为Biot 系数。1988 年,Detournay 和Cheng[13]根据Biot 理论,将充满流体的岩石假定为具有可压缩特性的多孔弹性材料,使用拉普拉斯变换推导得到钻井和垂直钻孔加压引起的应力、应变和孔隙压力的理论模型。20 世纪90 年代初期,Zimmerman、Berryman[14-15]研究了有效应力作用下非均质多孔岩石的表现。1993年,Detournay 和Cheng[16]的研究显示,孔隙压力的增加会引起岩石的膨胀,如果在不排水的条件下,即流体不能自由流入和流出时,岩石的压缩会导致孔隙压力的增加;其次在孔隙内流体与外界流通时,岩石的刚度比不流通的岩石更小。1995 年,Vardoulakis 和Sulem[17]将多孔介质弹性力学应用于地质力学分析中。Coussy 在前人的理论基础上,考虑了温度对多孔介质力学行为的影响,并建立了孔隙介质模型[18-19]。曾强[20]等人利用重力法、压汞法、氮吸附解吸附法测量了水泥石水化过程孔隙结构的变化。Ghabezloo 等人进行过水泥石的多孔介质力学实验的相关研究,测量得到水泥石的Biot 系数和本构方程参数,验证了水泥石力学性能受孔隙水压的影响,并针对排水、不排水实验条件对水泥石有效模量进行了进一步探索[21-22],后续又在此基础上与Vu[23]等人研究了油井水泥在不同温度下养护不同时间后水泥石体积应变的非线性规律。以上各研究表明,水泥石作为一种多孔介质会受到孔隙水压的影响,从而改变其力学性能。
为了准确描述水泥石在不同工况下的力学性能,基于多孔介质力学理论,开展了一系列考虑孔隙水压的水泥石三轴力学实验[24-25],得到水泥石在不同条件下的破坏强度,进而建立了基于有效应力原理的水泥石摩尔-库伦破坏准则,实现了水泥石在孔隙水压、围压作用下真实的强度及其力学行为描述,为井筒水泥在不同工况下的力学分析与预测提供了理论支持及数据支撑。
1 实验理论
1.1 多孔介质力学
多孔介质力学理论是在弹性力学理论的基础上,将固体物质内部的孔隙结构考虑进来。孔隙内流体的压力会对水泥石整体力学性能产生影响。基于Biot 理论的多孔介质力学本构模型如下[12]。

式 中,σ'为 有 效 应 力,MPa;K为 体 积 模 量,MPa;P为孔隙水压,MPa;ε为正应变,无量纲;b为 Biot 系数;φ为孔隙率,无量纲;N为Biot模量,MPa;G为剪切模量,MPa;τij为剪切应力,MPa;γ为剪切应变,无量纲。
其多孔介质对应的是固井水泥石,孔隙内流体是水。因为流体即孔隙水不抗剪切,所以在公式(1)中,孔隙水压(以下简称孔压)只对水泥石正应变产生影响,不会影响剪应变。大量前人实验和实践表明,Biot 系数为1 时,有效应力公式在饱和多孔介质中适用。所以在考虑剪切破坏准则时,可以将多孔介质有效应力原理简化为Terzaghi 有效应力原理[10,18]。选择压力为正,基于Terzaghi 有效应力原理的状态方程为:

式中,σ为总应力,MPa。由公式(2)可以看出,在孔压的影响下,总应力不变时,固体骨架受到的有效应力σ'随孔压增大而减小。有效应力不变时,水泥石整体强度随孔隙水压的增大而增大。在多孔介质内存在饱和流体且与外界流体相通时,孔压只与孔隙内外相通流体的压力有关,实验中的这种情况简称为排水条件[26],在多孔介质本身与外界不连通的情况称为不排水条件[27]。因此,在实验中,排水条件下的孔隙水压变化可以通过外界流体压力被定量控制。
在排水条件下,水泥石三轴破坏实验中,轴向有效应力为:

式中,σ1'为最大主应力有效应力,MPa;σ1为最大主应力,MPa;径向围压为:

式中,σ2为第二主应力。径向有效应力为:

排水三轴破坏实验的应力应变曲线中,有效差应力为:

在不排水三轴破坏实验的应力应变曲线中,差应力为:

1.2 摩尔-库伦准则
摩尔-库伦破坏准则(Mohr-Coulomb 准则)是判断水泥石力学状态比较常用的一种破坏准则。Mohr[28]假定,当试件的某一平面由于剪应力过大而发生剪切破坏时,这种破坏可以用函数关系表示:

式中,τ为剪切应力,MPa;σ为正应力,MPa。
因为τ的正负号仅仅影响滑动的方向,所以仅仅考虑τ的数值。在τ-σ平面内,上式表述为一条曲线(包络线)。该曲线将应力状态的安全区和破坏区分割开来,代表材料内部任意一点的应力状态(σ,τ)位于曲线之下时,破坏不发生;反之,破坏会发生。低围压条件下,函数f(σ)表现为线性,摩尔-库伦准则可以表示为[28]。

式中,C为内聚力;φ为内摩擦角。式(9)中的应力替换为有效应力得到:

其中,σ'的三轴摩尔-库伦公式为
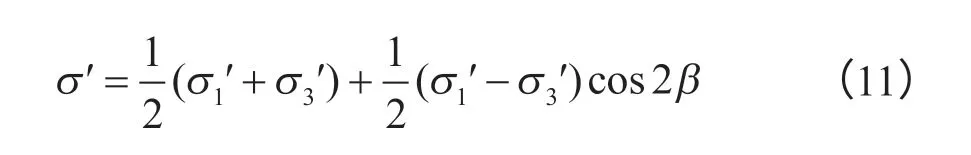
式中,2β为摩尔圆与包络线切点方向。通过应力可以反推出水泥石的内聚力C和内摩擦系数tanφ。从公式(11)可以看出,水泥石的摩尔-库伦准则与轴向破坏强度和围压有关。根据摩尔-库伦准则,摩尔圆的直径是水泥石的差应力破坏强度,即式(6)、式(7),摩尔圆左端与x轴交点为围压。由实验条件和实验结果可画出摩尔圆,从而获得包络线。
2 实验描述
2.1 实验设备及试样
实验采用朝阳实验仪器有限公司的TAW-1000微机控制电液伺服水泥石三轴试验机系统,具备开展孔压实验的能力。实验样品采用嘉华G 级水泥与0.2%高温稳定剂DRK-3S、0.3%分散剂DRS-1S 和44%水调配的水泥浆进行制作。将搅拌均匀的水泥浆导入模具,模具高度为52 mm,直径为25.4 mm。将模具密封压盖后放入常压养护釜,在80 ℃下养护7 d[29]。7 d 后从养护釜中取出模具,放入凉水中冷却,然后打开模具取出水泥石,采用比重法对水泥石试样进行测量,得到初始湿重均值为47.80 g,干燥后均值为40.21 g,真空饱水湿重均值为47.59 g,干重湿重差值均值为7.38 g,水泥石密度为1.9 g/cm3。由干燥水泥石重量和真空饱水水泥石重量差可知水泥石中孔隙水重量为7.38 g,再由含水率公式(12)得到水泥石的含水率为18.35%,且证明直接养护得到的水泥石试样饱水程度良好。

式中,φw为含水率;mw为水泥石中自由水质量,g;ms为干水泥石质量,g。
实验证明水泥石在水浴箱中养护饱水效果比真空饱水效果更好。
2.2 实验方案
实验测量装置为应变传感器,可以测量得到水泥石的轴向和径向应变。围压和孔压加载方式采用应力控制,设计实验加载速度为50 N/min;轴向加载速率采用位移控制,加载速率为0.05 mm/min,轴向应变测量装置量程在4 mm,1~3 mm 范围内为测准区域。所以,应变测量装置从1 mm 左右开始测量。为避免超出测准区域,在应力应变曲线没有下降趋势的情况下,选择应变3%作为临界值。设置实验条件如表1 所示。
3 结果分析
3.1 应力-应变数据
为了对此配方的水泥石在不同围压条件下力学性能进行描述,进行了排水孔压0.1 MPa 三轴破坏实验,数据如表2 所示。在排水条件下,为了能更明显地阐述水泥石在不同围压下的力学表现,取各围压条件下与平均值最接近的水泥石试样实验过程原始数据,获得应力应变曲线如图1 所示。
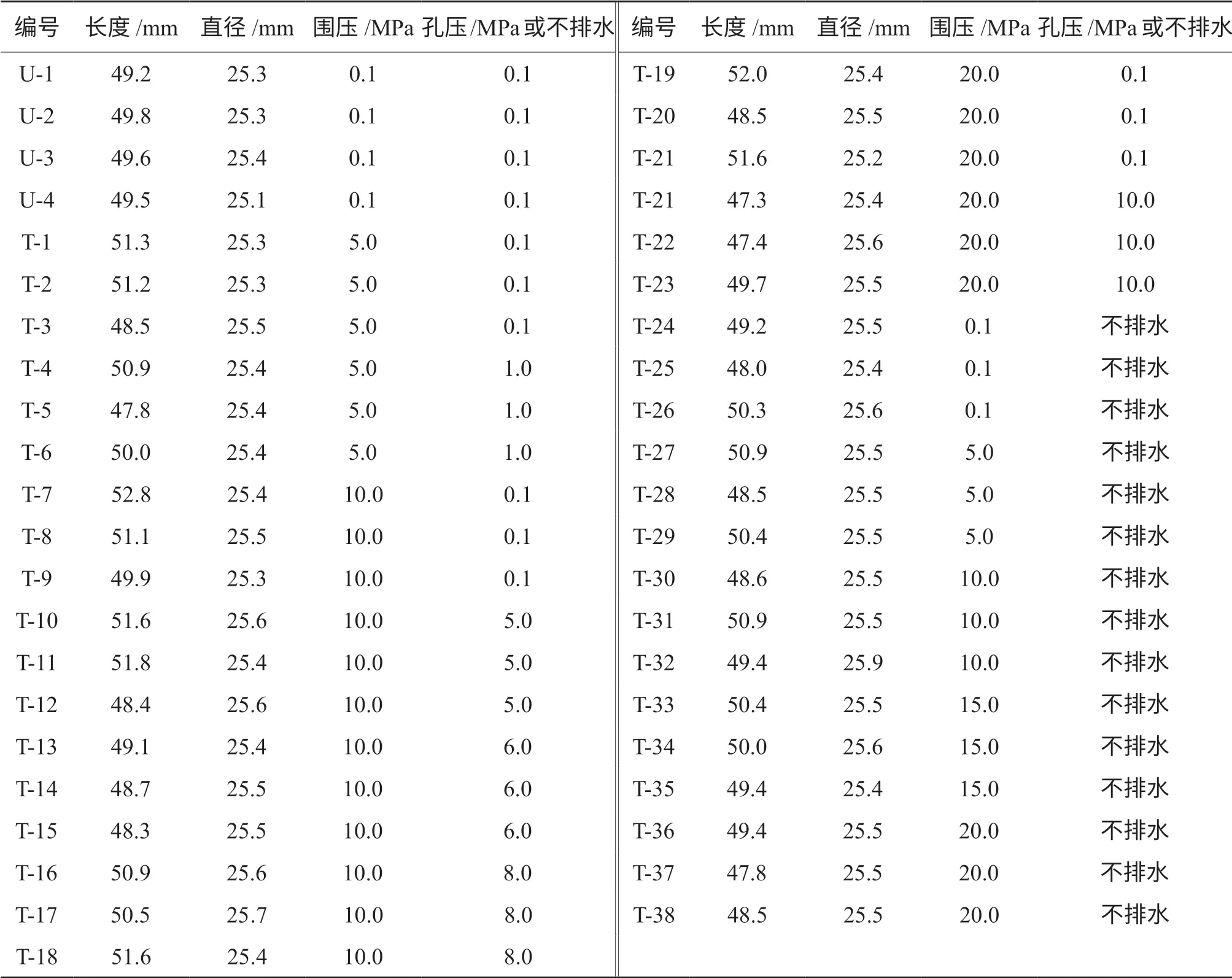
表1 试样信息及实验条件

表2 完全排水不同围压条件三轴力学实验结果
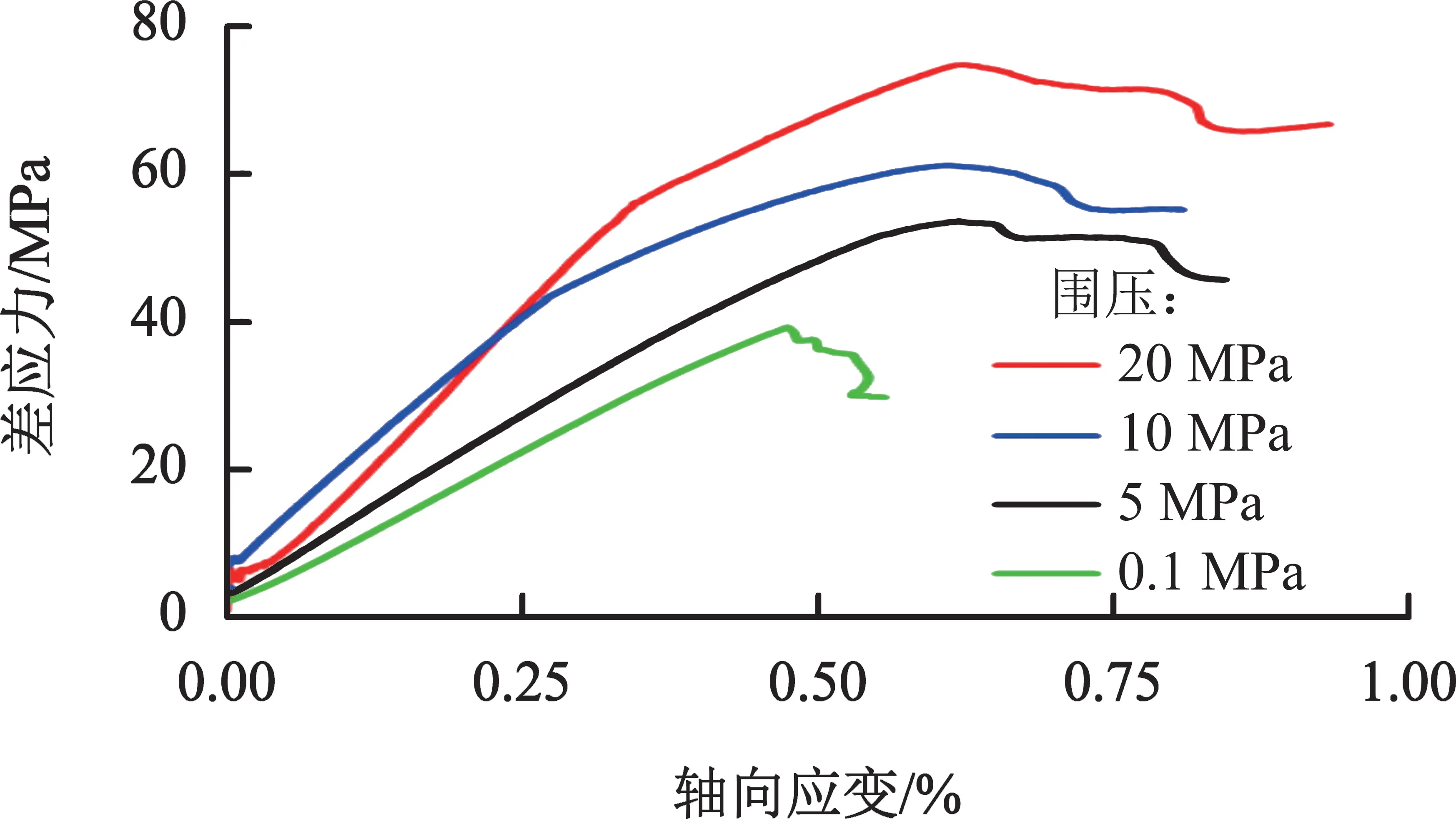
图1 完全排水条件下水泥石不同围压三轴强度破坏实验应力应变曲线
由图1 可以看出,围压越高,水泥石的破坏强度越高。由表2 可知,围压为20 MPa 时,水泥石差应力破坏强度均值达到66.5 MPa;围压为10 MPa 时,水泥石破坏强度均值为56.2 MPa;围压为5 MPa 时,水泥石破坏强度均值为52 MPa;围压为0.1 MPa,即单轴实验时,水泥石破坏强度均值为38.4 MPa。三轴试验机围压加载在水泥石3个正应力方向,水泥石孔压为常压并保持不变,受围压作用水泥石整体体积变小,水泥石骨架在围压作用下更密实,孔隙变小,饱和水泥石中流体被挤压,离开水泥石内部进入三轴实验机孔隙水压的水压箱中,水泥石密度增加,强度增强。在摩尔-库伦准则中,围压越大,差应力峰值强度越大,且构成的摩尔圆半径越大,实验结论与理论相符。
为了探究孔隙水压对水泥石力学性能的影响,在围压10 MPa 的实验条件下,进行不同孔隙水压的三轴破坏实验,具体的实验数据如表3 所示。

表3 围压10 MPa 下不同孔隙水压三轴力学实验结果
由表3 可知,围压为10 MPa 时,孔压为8、5和0.1 MPa 的水泥石差应力峰值均值分别为55.7、56.6 和63.2 MPa(计算时去掉与均值相差过大的离散数据)。根据水泥石差应力峰值均值数据,水泥石的破坏强度受到孔隙水压的影响,孔隙水压越大,水泥石破坏强度越低。根据式(3)、(6)得到水泥石轴向破坏应力值在孔压为8、5 和0.1 MPa时分别为59.3、62.3 和66.1 MPa,说明水泥石骨架的破坏强度随着孔压的增加而逐渐降低。由此认为,将水泥石骨架理解为框架连接,围压从外部加载,使框架被压紧,更不易破坏,但是孔隙水压从框架之间加载,作用于框架的各个方向,使压紧的框架变松散,从而使水泥石骨架的破坏强度降低,导致整体水泥石强度降低。基于多孔介质理论的摩尔-库伦准则理论也能解释这一现象:相同围压时,孔压越大,破坏强度减小,由式(5)可知,最小主应力的有效应力值减小,导致摩尔圆整体左移且半径减小,而对应的包络线斜率降低,意味着内摩擦角的减小,材质更加松散。
根据表3 可知,在不同孔压条件下,水泥石的三轴强度破坏实验的应力-应变变化如图2 所示。由图2 可知,围压为10 MPa 排水三轴实验中,水泥石差应力破坏强度与孔压是具有一定关系的。随着孔隙水压的增加,孔隙内部流体对水泥石骨架的作用力增加,水泥石骨架外扩,孔隙体积逐渐变大。因为外部围压限制了孔隙体积的增加,所以水泥石整体体积应变小于加载围压时的体积应变。

图2 围压10 MPa 水泥石不同孔压三轴强度破坏实验应力应变曲线
3.2 水泥石摩尔-库伦准则分析与应用
为了验证基于多孔介质力学的摩尔-库伦准则的实际意义,设计实验围压不同,孔隙水压不同的四组排水三轴破坏实验,数据如表4 所示。
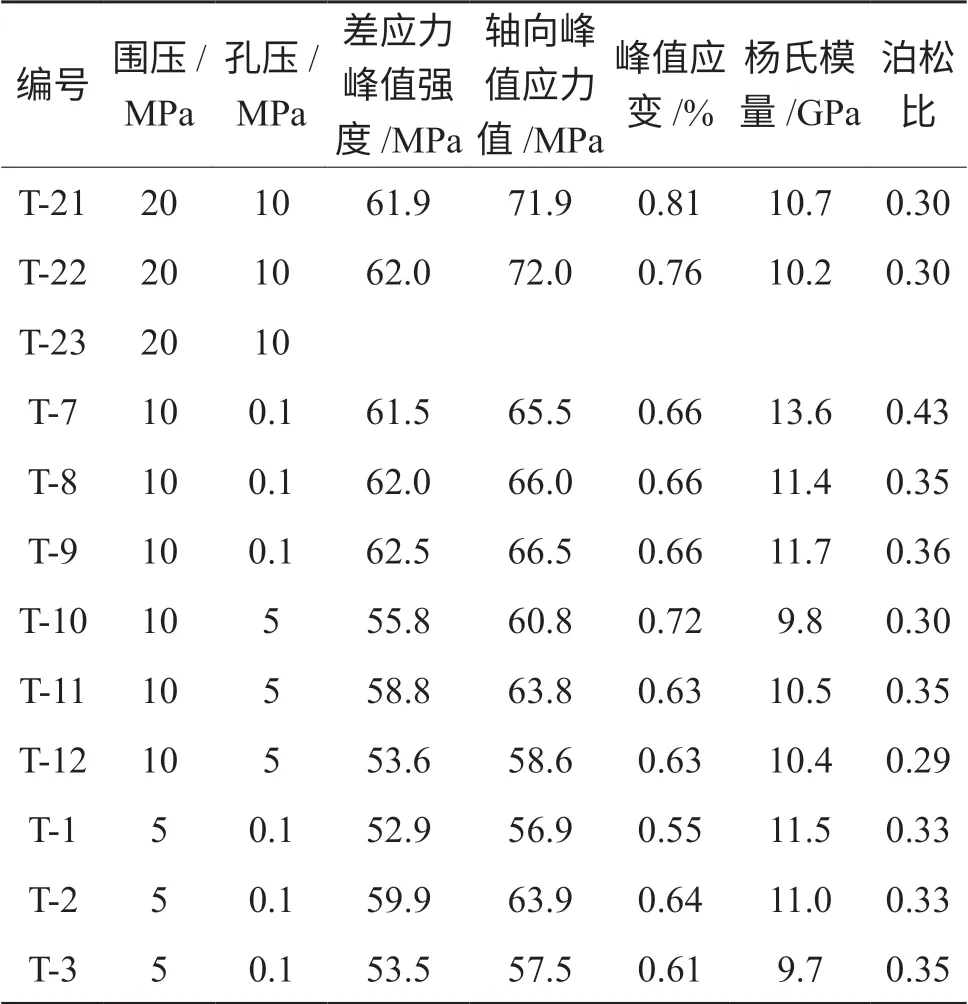
表4 排水条件下不同孔隙水压三轴力学实验结果
由表4 数据画出基于有效应力的摩尔库伦圆如图3 所示。图3 中显示围压与孔压的压差越高,水泥石的破坏强度越高。由公式(6)和(7)可知,水泥石骨架的破坏强度是最大主应力减去孔隙水压。当围压与孔压的压差相同时(即摩尔圆的左端起点一致),不同围压下的差应力(摩尔圆大小)也一致,这证明实验规律符合基于多孔介质力学的摩尔-库伦准则。
对养护7 d 的水泥石在不同围压和孔隙水压条件下进行实验,画出摩尔库伦圆,并对所有的摩尔圆进行切线线性回归得到摩尔-库伦包络线,如图4 所示。
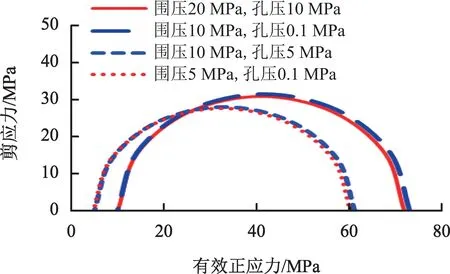
图3 水泥石排水三轴强度破坏实验摩尔圆
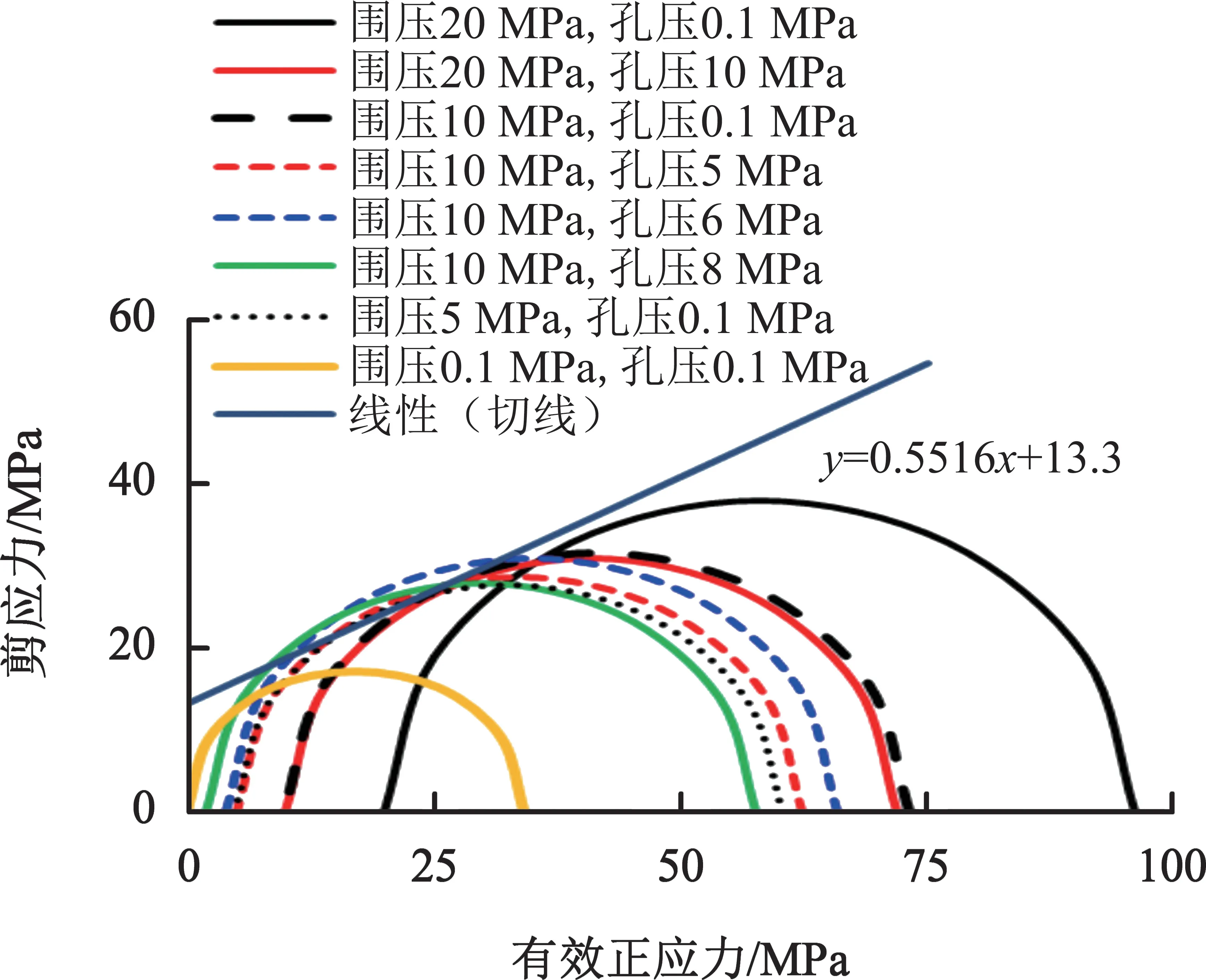
图4 油井水泥石排水条件下三轴强度破坏实验有效应力摩尔库伦准则
基于有效应力原理,将实验数据代入式(10)和式(11),计算出水泥石骨架的内聚力为13.3 MPa,内摩擦系数为0.5516。最后确定纯油井水泥石作为多孔介质的摩尔-库伦破坏准则为如下。

为了证明不排水试验与排水试验水泥石破坏准则存在差异,进行不同围压不排水三轴试验,得到数据如表5 所示。
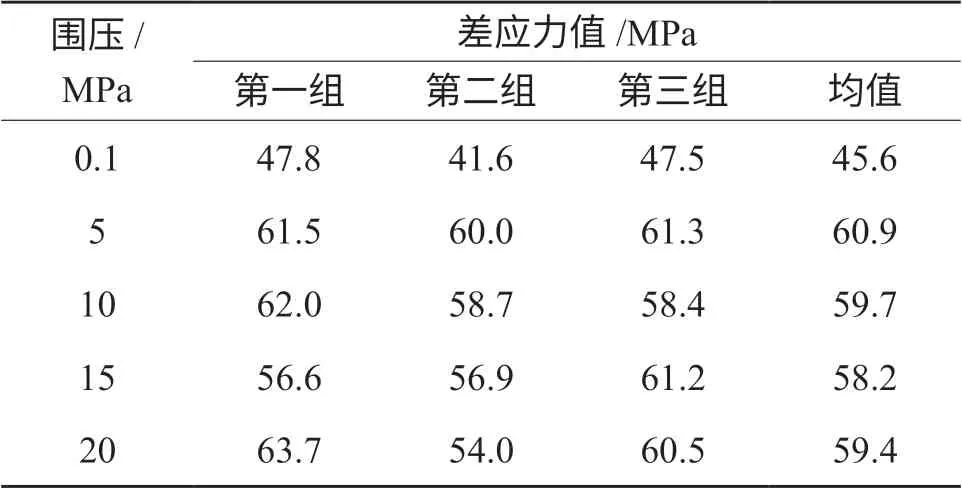
表5 不排水三轴力学破坏强度实验结果
表5 表明围压超过5 MPa 之后,围压越高,剪应力峰值数据变化浮动,没有呈现出递增的趋势。摩尔圆半径变化不大是这种现象的直观表现,如图5 所示。图5 中的摩尔圆分布验证了线性摩尔-库伦准则不适合高围压不排水三轴试验,高围压时摩尔圆切线与低围压摩尔圆无法形成一条直线,且围压越高的摩尔库伦圆,相互之间的切线越趋于平行x 轴,符合非线性摩尔库伦包络线。
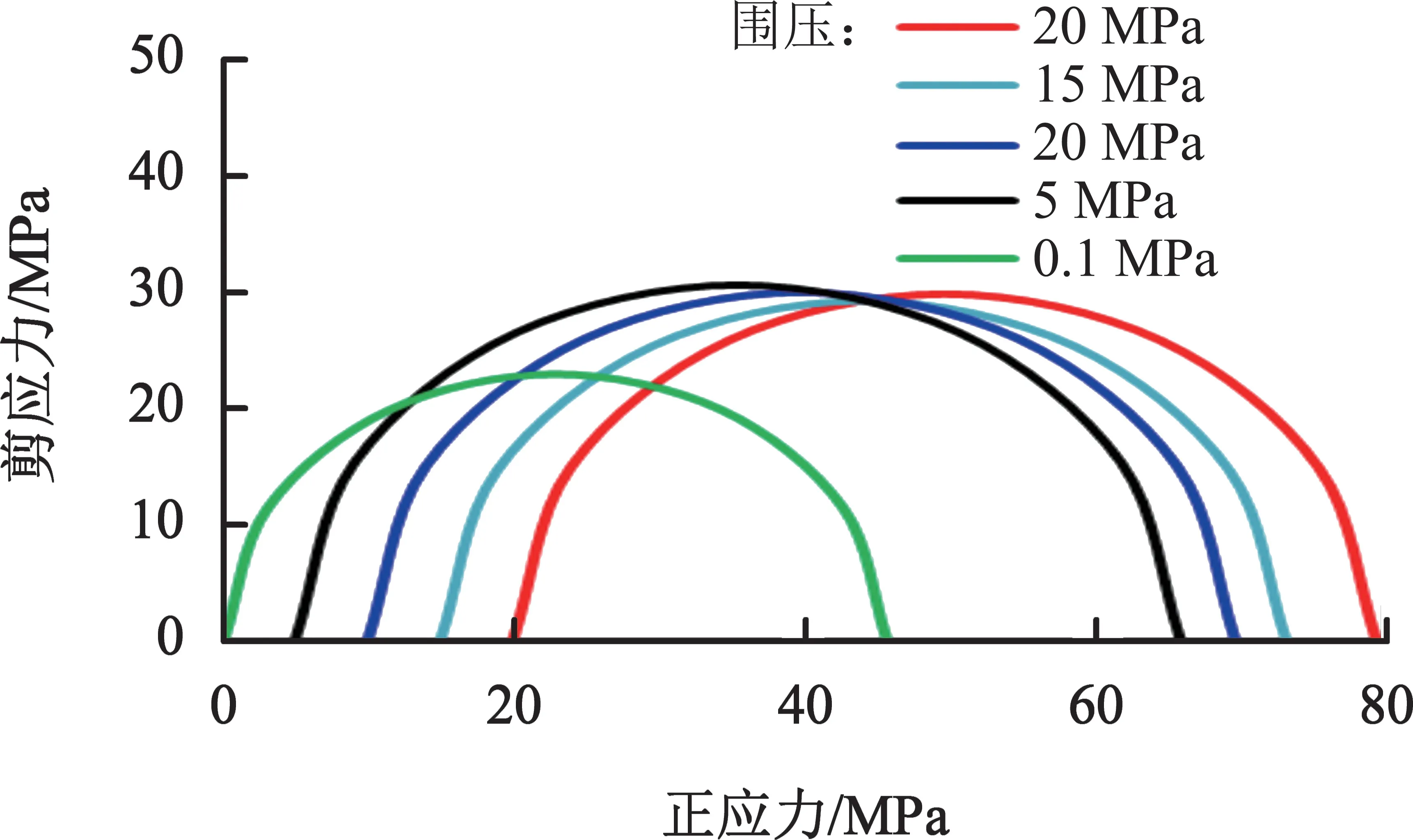
图5 水泥石不排水条件下三轴强度破坏实验摩尔-库伦圆
4 结论
1.排水实验条件下孔隙水压是影响水泥石破坏强度的因素。围压相同时,随着孔压增大,水泥石骨架破坏强度逐渐降低。围压和孔压压差相同时,水泥石破坏强度不变。
2.不排水实验条件下孔隙水压随外压变化而变化。数据显示,高围压条件下的破坏行为不符合线性摩尔库伦准则,如果用线性摩尔库伦准则进行预判,会高估封闭条件下水泥石的破坏强度。
3.与不排水实验数据图对比发现,排水实验水泥石即使在高围压条件下也能符合线性摩尔-库伦准则,摩尔圆半径随着右移逐渐增大,水泥石的破坏强度逐渐增加。
4.该次实验获得常规G 级水泥石骨架内聚力为13.3 MPa,内摩擦系数为0.55;建立基于有效应力的纯油井水泥摩尔库伦破坏准则。
