基于p阶Welsch损失的鲁棒极限学习机

陈剑挺， 叶贞成， 程 辉

（华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海 200237）

极限学习机(ELM)[1]是一种机器学习算法，一种有监督的单隐层前馈神经网络（SLFN）。它通过随机生成输入权重和偏置的方式将输入映射到高维隐层空间，具有训练速度快、泛化精度高的特点，并且该算法已被证明具有通用逼近能力[2]，因此，ELM已被广泛应用于回归、分类等问题之中，如风电预测[3]、故障检测[4]、醋酸精馏软测量[5]、图像识别[6]等。针对该算法输入权重不能改变的缺点，近些年开发了一些新的技术对ELM算法进行改进[7-8]，但都是基于最小二乘法（Least Square，LS）来求解ELM的输出权重矩阵。最小二乘法的目标是学习未知的映射（线性或非线性），使得模型输出和标签值之间的均方误差（Mean Square Error，MSE）最小化。在均方误差损失中所有数据样本所占的权重都相同，因此当数据中有异常值存在时，最小二乘法为了达到极小化残差平方和的目标，必须迁就异常值，这往往会导致参数估计存在较大的偏差[9]。

为了减少数据中的异常值对算法参数估计的影响，Deng等[10]提出了一种基于加权最小二乘法的正则化鲁棒ELM，通过对各个数据样本赋予不同的权重以增加算法的鲁棒性。Zhang等[11]提出了基于范数的损失函数和 l2范数正则项的鲁棒ELM，该算法使用增广拉格朗日乘子算法来极小化目标损失函数，有效地减少了异常值的影响。Xing等[12]用最大相关熵准则（Maximum Correntropy Criterion，MCC）代替最小均方误差准则，从而提高了算法的泛化性能和鲁棒性。Horata等[13]提出了基于Huber损失函数的鲁棒ELM，并使用迭代重加权最小二乘（IRLS）算法来求解Huber损失函数的优化问题，但是该损失函数中并没有引入避免参数过拟合的机制。依据M估计理论，Chen等[14]提出了一个统一的鲁棒ELM框架，分别利用 l1范数正则项和 l2范数正则项来避免过拟合，利用4种损失函数（ l1范数、Huber、Bisquare、Welsch）提高ELM网络的鲁棒性，并采用IRLS算法来求解，但同时指出对于 l1范数正则项，IRLS算法并不是最佳选择，快速迭代阈值收缩算法（FISTA）[15]算法在解决 l1范数正则项问题时比IRLS 算法更高效。

Welsch估计方法是稳健估计（Robust Estimation）M估计中的一种方法。Welsch损失是基于Welsch估计方法的损失函数。当数据误差呈正态分布时，它与均方误差损失效果相当，但当误差呈非正态分布，如误差是由异常值引起时，Welsch损失比均方误差损失更具鲁棒性[14]。而且基于二阶统计度量的均方误差损失函数对数据中的异常值敏感，容易受到异常值的影响，并不是鲁棒学习中的好方法[16-18]。

为了使算法兼具极限学习机的高效性和Welsch估计对异常值的鲁棒性，本文提出了一种基于 p 阶Welsch损失的鲁棒极限学习机算法。首先，提出了基于MPE（Mean p-Power Error）[17]改进的 p

阶Welsch

损失函数，并用该损失函数替代ELM目标函数中的均方误差损失；其次，在目标函数中引入 l1范数正则项来获得稀疏的ELM网络模型，防止模型过拟合，提高模型的稳定性，并采用快速迭代阈值收缩算法极小化改进的目标函数。在人工数据集和典型的UCI数据集上的仿真实验结果表明，本文算法在保证ELM网络稳定性的同时提高了模型的鲁棒性，并且缩短了训练时间。

1 极限学习机

ELM模型结构如图1所示。

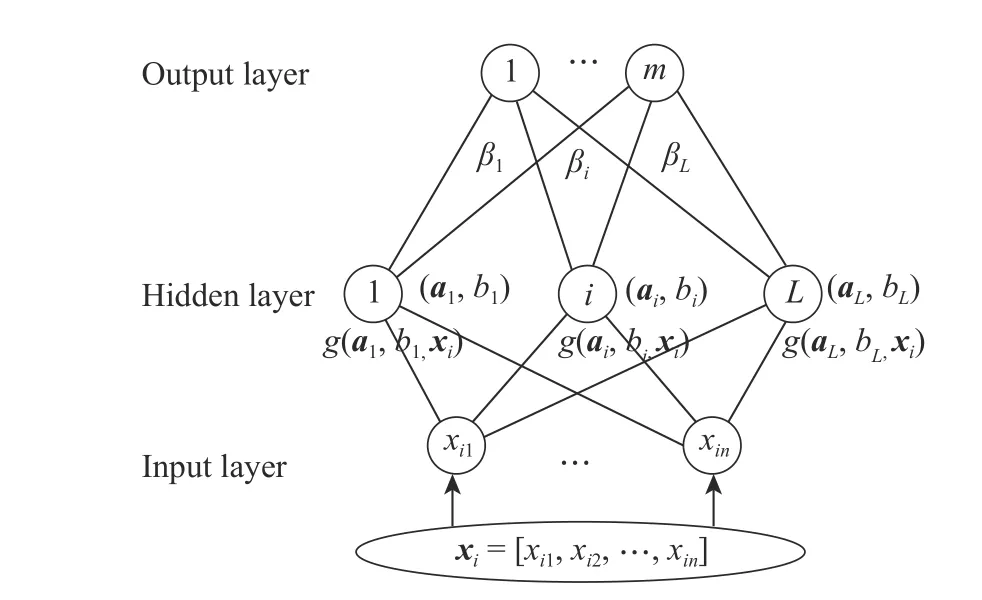
图 1 ELM模型结构图Fig. 1 Model structure of ELM

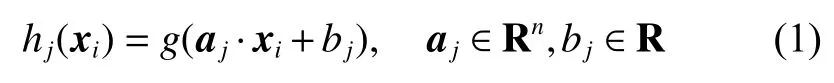
{xi,xi}Ni=1

对于数据集，ELM的隐层输出为

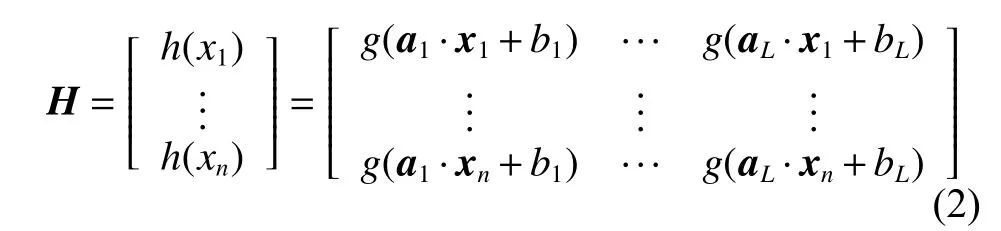
T是数据集标签：

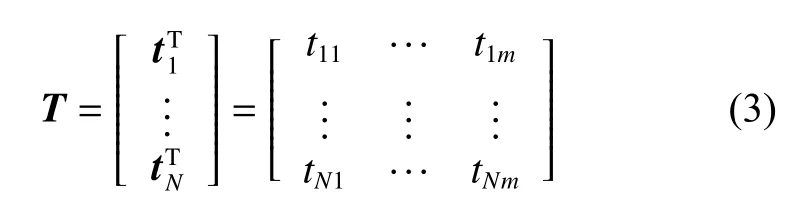
β∈RL×m是输出权重矩阵：

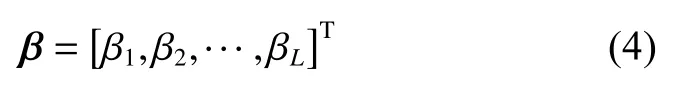
输出节点对输入 xi的预测结果如下：

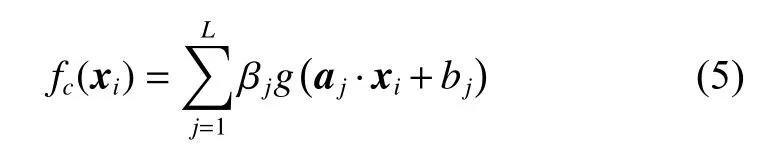
对于ELM算法，其输入权重矩阵 a 和偏置量 b是随机确定的，确定之后即不再改变。因此，网络训练的目标函数为

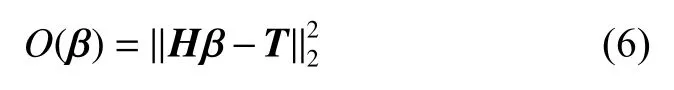
其中，‖·‖2为 l2范数。

采用最小二乘法求解式（6）中的目标函数，得到隐层的输出矩阵：

其中，H†是隐层输出矩阵H的Moore-Penrose广义逆矩阵：

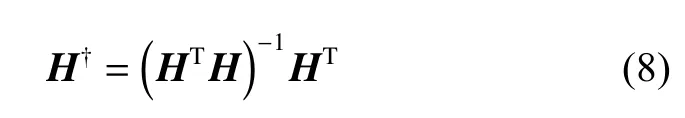
为了进一步提高ELM的稳定性以及泛化能力，文献[2]提出了正则化ELM（RELM），网络的目标函数如下：

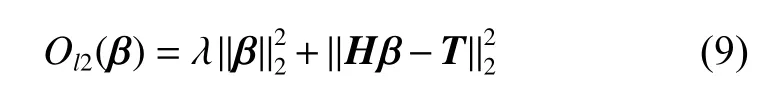
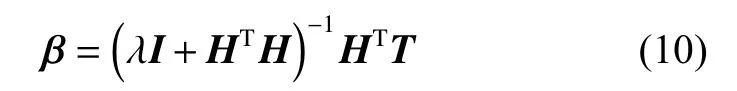
2 基于p阶Welsch损失的鲁棒ELM

ELM算法中的目标函数是均方误差（MSE）损失，该损失项对每个样本数据给予了相同的权重，这使得异常值对误差平方和的影响比其他数据大，导致参数估计对于异常值相当敏感。如图2所示，均方误差损失相比Welsch损失对异常数据更敏感。为此，本文提出了一种基于MPE改进的 p 阶Welsch损失作为损失函数来改进算法的鲁棒性。

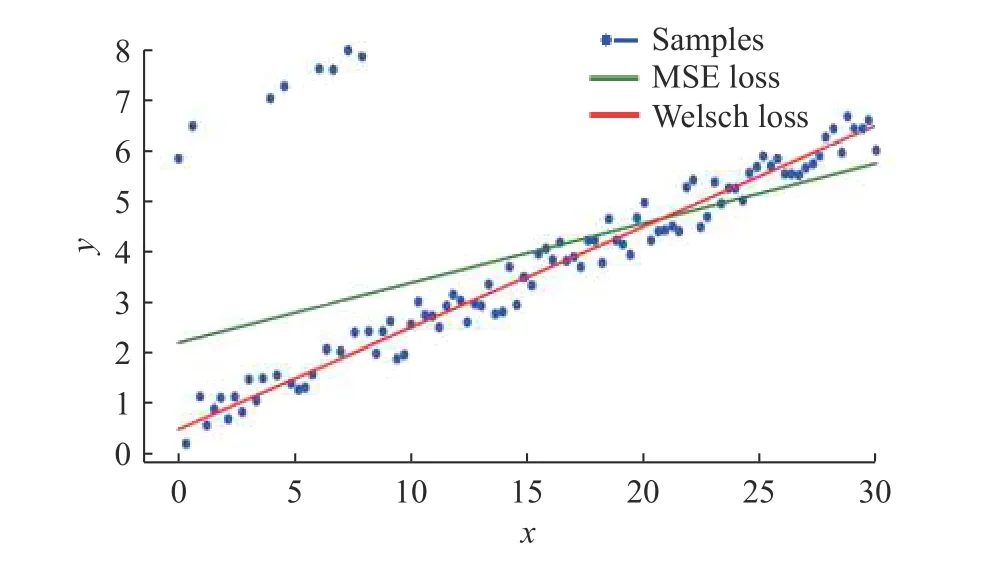
图 2 有异常值数据时不同损失函数下的拟合效果图Fig. 2 Fitting effect graph of different loss functions with outlier data

2.1 基于MPE改进的p阶Welsch损失函数

Welsch损失[14]表示如下：

文献[16-18]提出将误差的 p 阶次函数作为损失函数，并指出适当的 p 值可以更好地处理异常值。本文基于MPE对Welsch损失函数进行改进，提出了 p 阶Welsch损失函数，如式（12）所示。

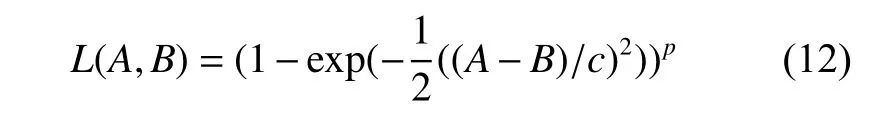
每个样本的 p 阶Welsch损失可以表示为

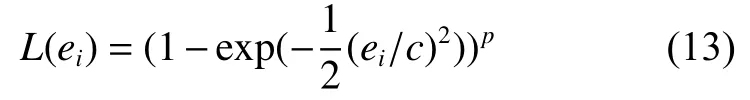
yi为对应样本xi模型的响应值，ti为样本的标签值，ti-yi代表残差，med(|err|)代表所有残差绝对值的中位数。

p 阶Welsch损失的梯度函数如下：

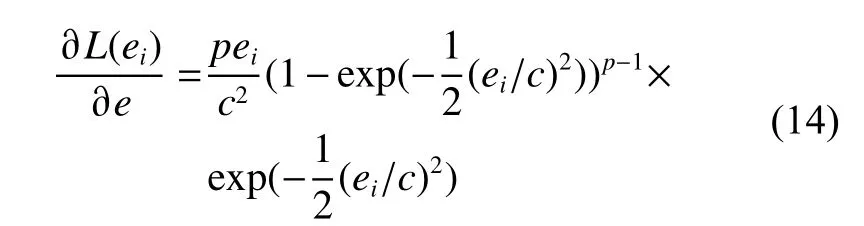
图3为 p 阶Welsch损失函数、MSE损失函数及其梯度函数的比较图。从图中可以看出， p 阶Welsch损失中每个样本的误差控制在了0～1之内，且其梯度函数在误差超过一定值之后会减小，并不会像平方损失项的梯度函数一样随着误差的增大而增大，从而降低了异常值引起的大误差项对于参数估计的影响力。

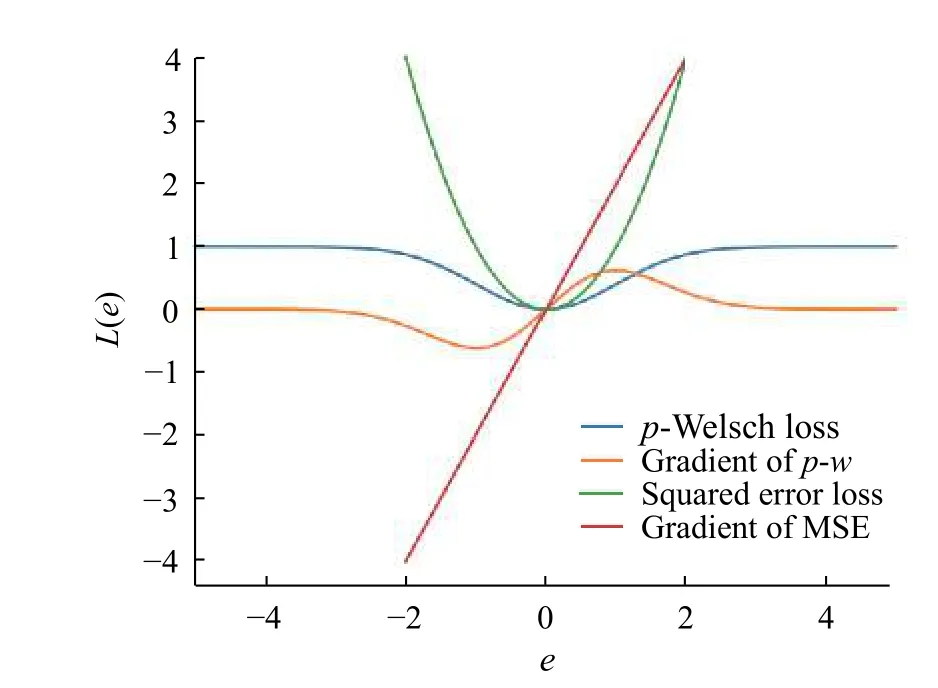
图 3 损失函数及其梯度函数比较图Fig. 3 Comparison graph of loss function and its gradient function

对于不同的 p 和 c ， p 阶Welsch损失函数的曲线如图4、5所示。分析图4中的变化趋势可以看出，对于任意 p值，p 阶welsch损失函数都会随着误差的增大而增大，最终会在误差达到一定阈值时趋近于1.0，之后即使误差再增加， p 阶Welsch损失也只是再向1.0靠近，变化甚微，从而降低了异常值带来的大误差对模型训练的影响程度。并且，随着 p 值的减小， p阶Welsch损失函数的梯度函数的极值点会随着 p 值的减小而前移，即 p 阶Welsch损失函数关于误差变化最敏感的部分相对前移，因此，当 p 值过大时， p阶Welsch函数对于异常值的敏感程度会增加。

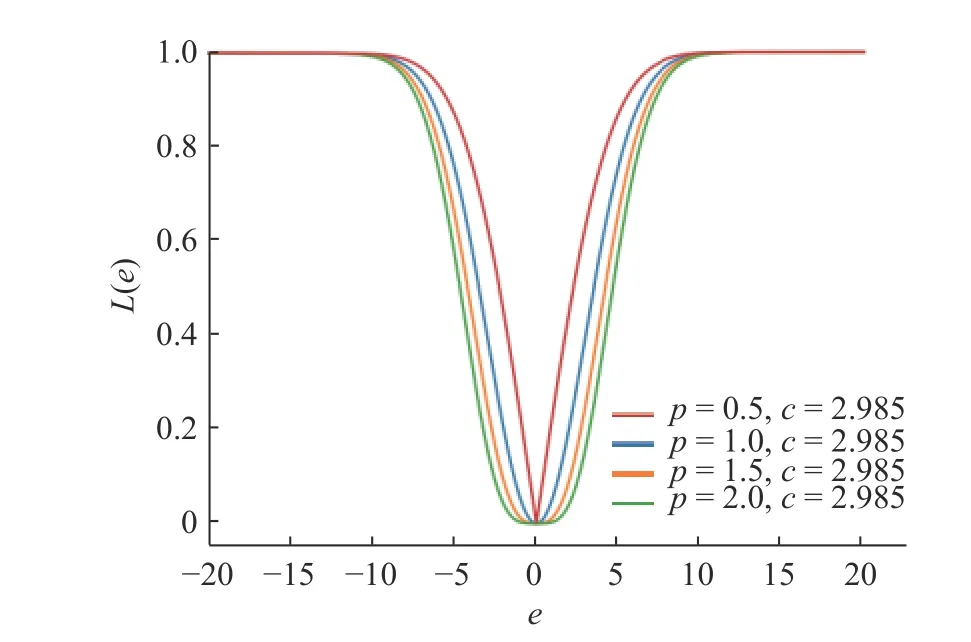
图 4 p 阶Welsch损失在不同参数 p 下的曲线Fig. 4 Curves of p-power Welsch loss functions under different P

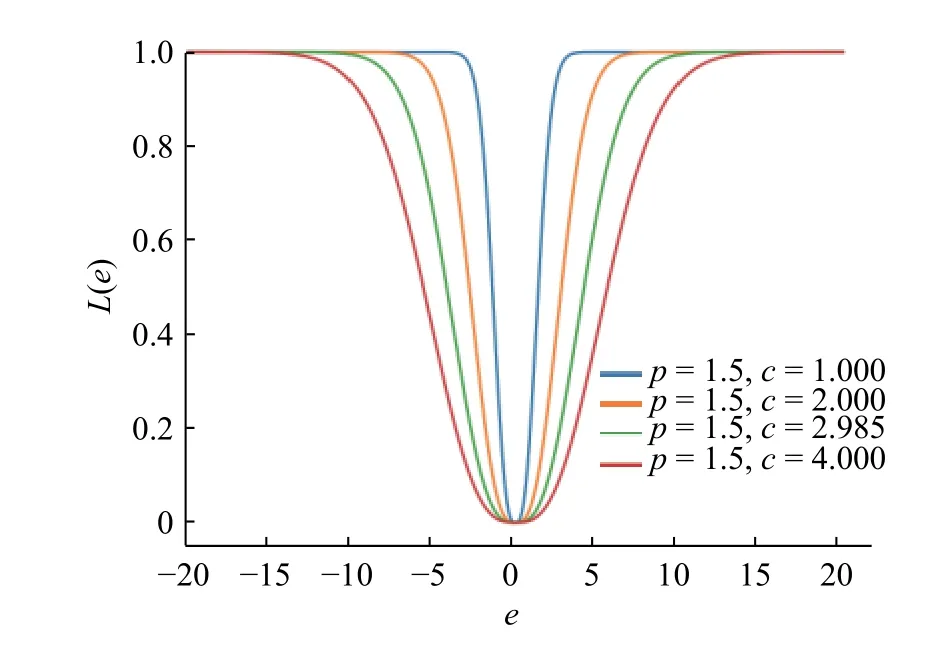
图 5 p 阶Welsch损失在不同参数 c 下的曲线Fig. 5 Curves of p-power Welsch loss functions under different c

图5示出了 p 阶Welsch损失函数在不同 c 值下的变化趋势，从中可以看出，随着c值的增大， p 阶Welsch损失趋近于1.0时对应的误差值也会相应地增大。因此可以通过调整 p、c来降低 p 阶Welsch损失函数对于异常值的敏感程度。

为了得到对异常值更具鲁棒性的ELM网络模型，将 p 阶Welsch损失函数代入到式（6）中，代替均方 误差损失，得到目标函数如式（15）所示：

2.2 优化算法

为了控制ELM网络模型的复杂度，提高模型的稳定性，本文在目标函数中引入了正则项。最简单的正则化形式之一是 l2范数，在目标函数中加入它可以促使输出权重矩阵 β 中的值向0逼近但不为0。另一种常用的正则化是 l1范数，也被称为lasso，当正则化因子 λ 足够小时，该范数的加入可以将输出权重矩阵 β 中一些值训练为0，从而得到稀疏模型

[14]。本文在目标函数中引入了 l1范数正则项

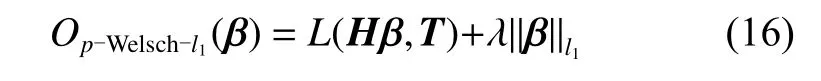
将式（16）改写为

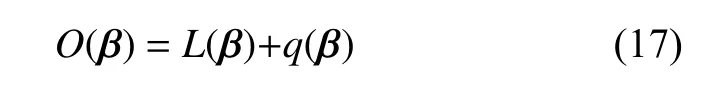
其中： L(β)=L(Hβ,T)；q(β)=λ‖β‖l1。损失函数 L(β)的梯度可以表示为

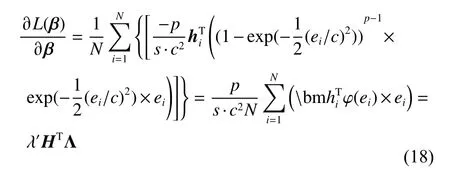
Λ 是对角线矩阵，并且

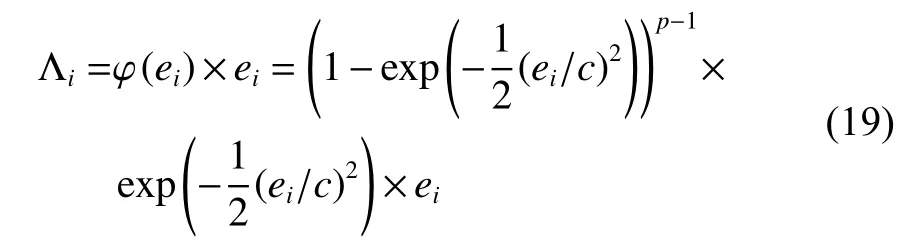
本文采用FISTA算法对目标函数（式（16））求极小值。优化算法计算步骤如下：

Algorithm 1 Robust ELM based on p-power Welsch loss and l1regularization: ELM-PW-l1Lλpcitermax

Input:

Output: β

Step 1 Randomly generate input weights matrix a ,and bias weight b

Step 2 Calculate the output weight matrix H

Step 3 Calculate Lipschitz constant y=max(eig(HT.H)) and the gradient of loss function ∇L

y1=β0∈Rnt1=1j=1

Step 4 Initialize

Step 5 Repeat when j ＜ itermax

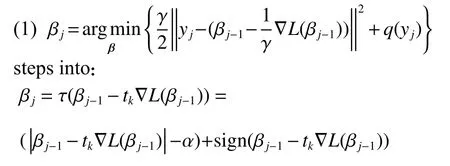
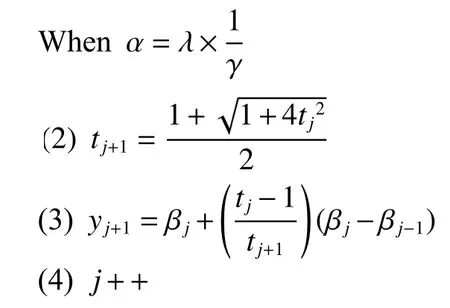
3 仿真实验

采用3.0 GHz CPU，16 GB RAM，64位主机，在Matlab2016b Win10环境下对算法进行测试。并与ELM、ELM-huber[13]、ELM-Welsch[14]、ELM-p-Welsch、ELM-PW-l1在人工合成回归数据集和UCI回归数据集上进行对比。其中ELM-Welsch、ELM-p-Welsch采用迭代重加权最小二乘（IRLS）[14]方法。选择均方根误差RMSE作为评价指标：

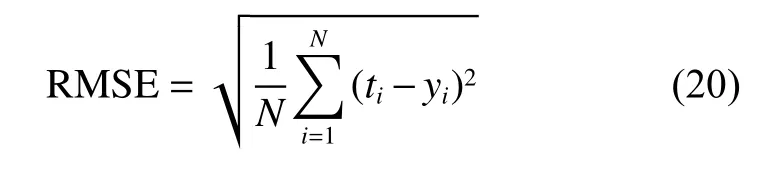
其中： ti和 yi分别表示样本的实际标签值和相应的算法预估值； N 为样本的数量。

3.1 算法参数设置

（1）输入权重矩阵 aN×L和隐层偏置量 bL×1在[-1,1]内 随机选取，隐层激活函数为 s igmoid 函数，定义为

（2）正则化参数 λ ，隐层节点{个数L通过交叉验}证的方式进行优选，其中 λ:10-10,10-9,···,1010;L:{10,20,30,···,150,200,300,500,1000} 。

（3）算法迭代次数 itermax=20

（4）参数 c 和阶次 p 也通过交叉验证的方式进行优选，其中 c:{0.1,0.2,0.3,···,2.5,3.0,3.5,5.0}；p:{0.1,0.2,0.3,0.4,0.5,···,3.0} 。

3.2 人工数据集实验结果

人工数据集由函数 (i)=sinc(x(i))+v(i) 生 成，其中：

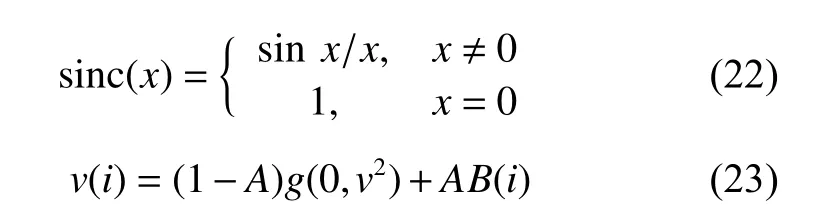
g(0,v2)表示均值为0、方差为 v2的高斯噪声； B(i) 模拟脉冲噪声；A用来控制添加到数据中的噪声类型。x(i) 均匀选自[-6,6]，生成数据集 {(x(i),y(i))}2i=0

10。通过交叉验证后，参数设置如下： L=100,λ=10-6,p=1.5,c=0.9 。

图6为5种方法在20% 异常值水平下的训练集回归效果图。其中ELM、ELM-huber、ELM-Welsch、ELM-p-Welsch、ELM-PW-l1的测试回归误差分别为0.216 3、0.115 9、0.107 2、0.105 9、0.103 9。由图6可知，与其他4种方法相比，常规的ELM对于异常值更敏感。

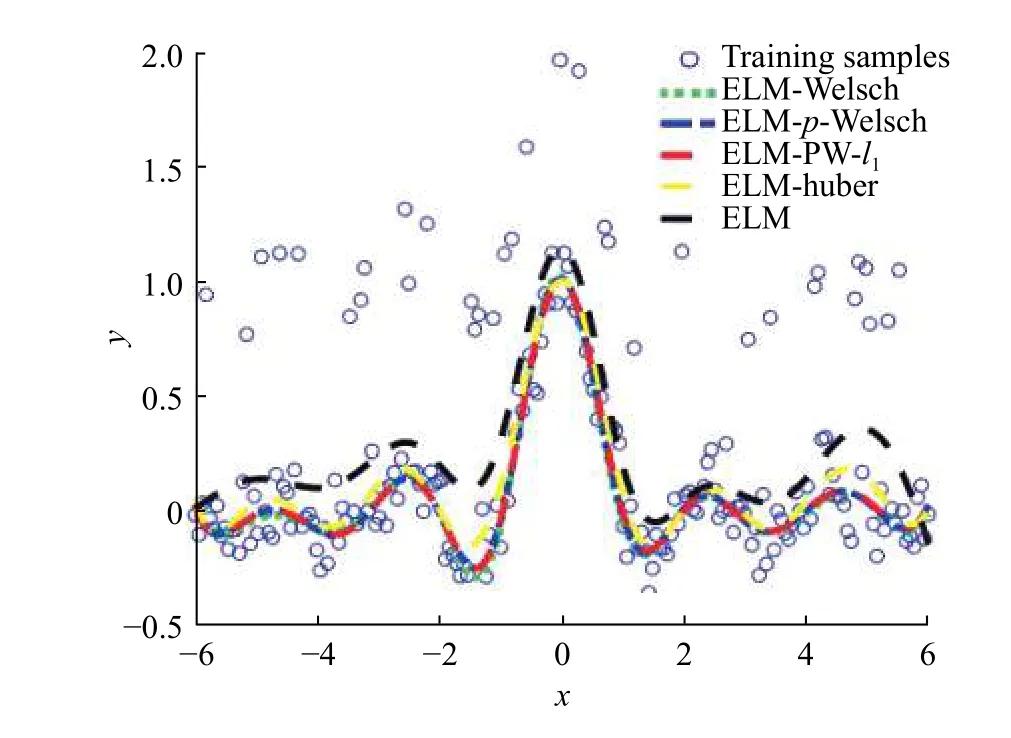
图 6 人工数据集在20%异常值下的训练结果Fig. 6 Training results of synthetic datasets with 20% outliers

表1示出了5种方法在不同异常值水平下的测试结果。由ELM和ELM-PW-l1的测试结果对比可得，随着异常值水平的增加，ELM的RMSE明显上升，而ELM-PW-l1的RMSE变化幅度不大，基本保持稳定，验证了该方法的有效性。

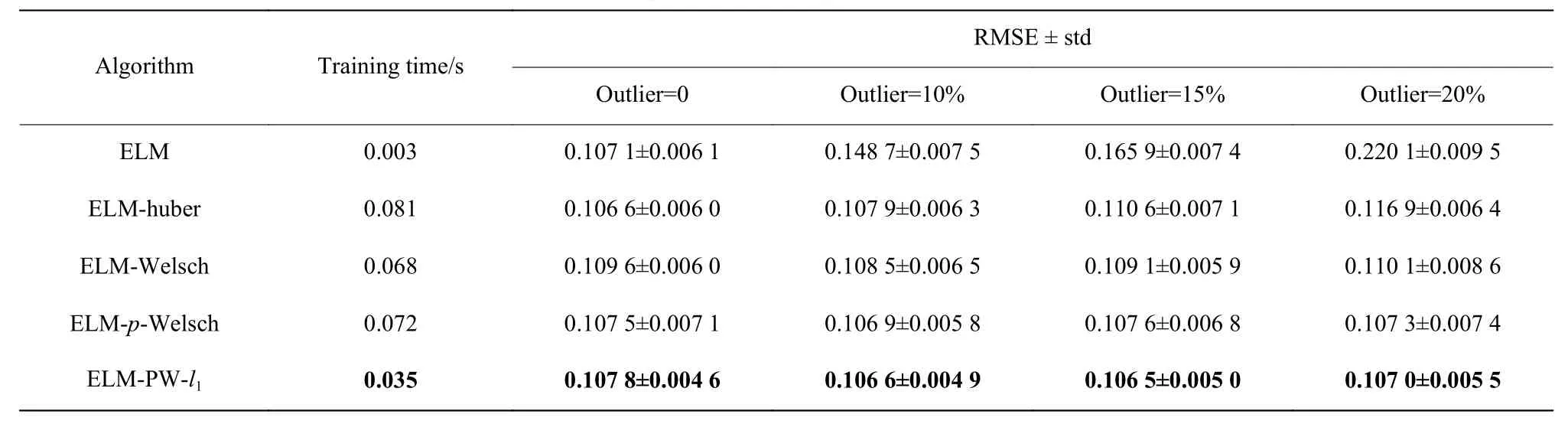
表 1 5种算法测试结果的RMSE和训练时长Table 1 RMSE and training time of five algorithms under different outlier levels

通过对比ELM-huber、ELM-Welsch、ELM-PWl1可得，ELM-PW-l1在训练效率上优于ELM-huber和ELM-Welsch，且RMSE也略优于二者，验证了该方法的先进性。

最后，通过对比ELM-p-Welsch和ELM-PW-l1的测试结果可得，在引入了 l1范数正则项后，ELM-PWl1的标准差要小于ELM-p-Welsch的标准差，该方法的稳定性得到了提高。

图7示出了不同参数 p 下算法的收敛结果。可以看出，不同参数 p 下算法的收敛结果不同，且当p=1.5 时，在上述参数中的收敛效果最好。

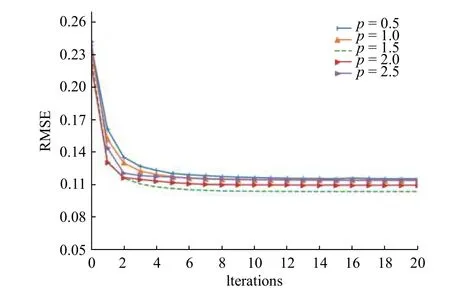
图 7 不同参数 p 下测试集的RMSE Fig. 7 RMSE of testing dataset under different p

3.3 UCI回归数据集实验结果

为了进一步验证本文方法的性能，通过UCI中的部分回归数据集对ELM、ELM-huber、ELM-Welsch，ELM-p-Welsch、ELM-PW-l1方法进行测试。所选数据集的信息如表2所示，随机选取其中的50%作为训练集，剩下的50%作为测试集，并且在训练集标签中添加了10%的异常值。表3为5种算法的参数设置表。

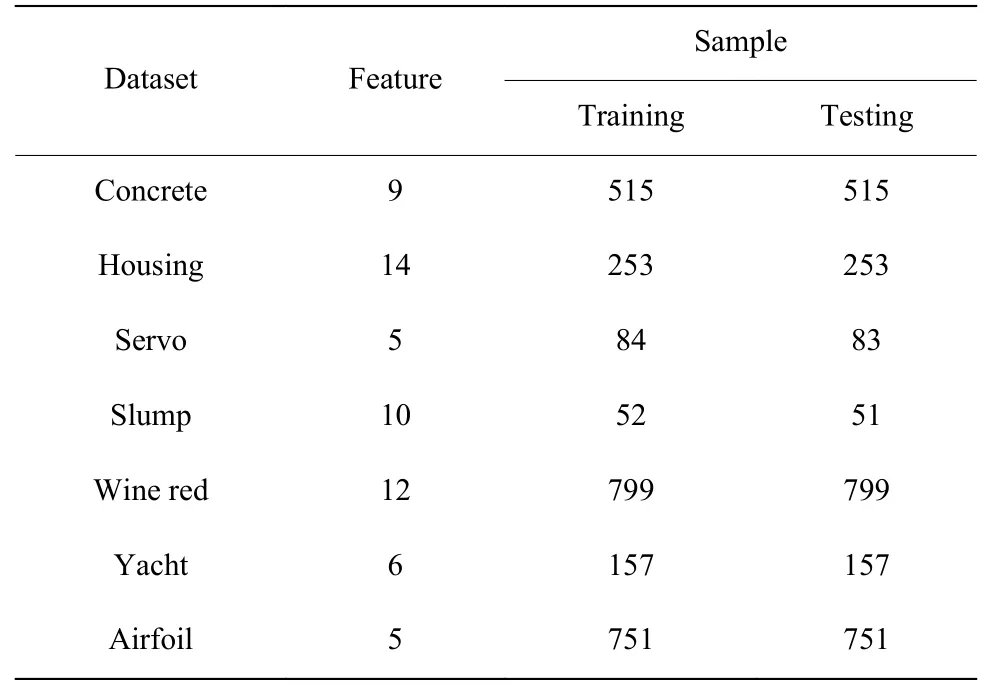
表 2 UCI回归数据集信息表Table 2 UCI regression dataset

由表4可知，ELM-PW-l1回归误差小于ELM、ELM-huber、ELM-Welsch和ELM-p-Welsch，同 时RMSE的标准差相比其他4种算法也更小，说明本文方法在抗异常值方面具有更好的鲁棒性，同时也具有更好的稳定性。

表 3 算法参数设置Table 3 Parameter settings of algorithms

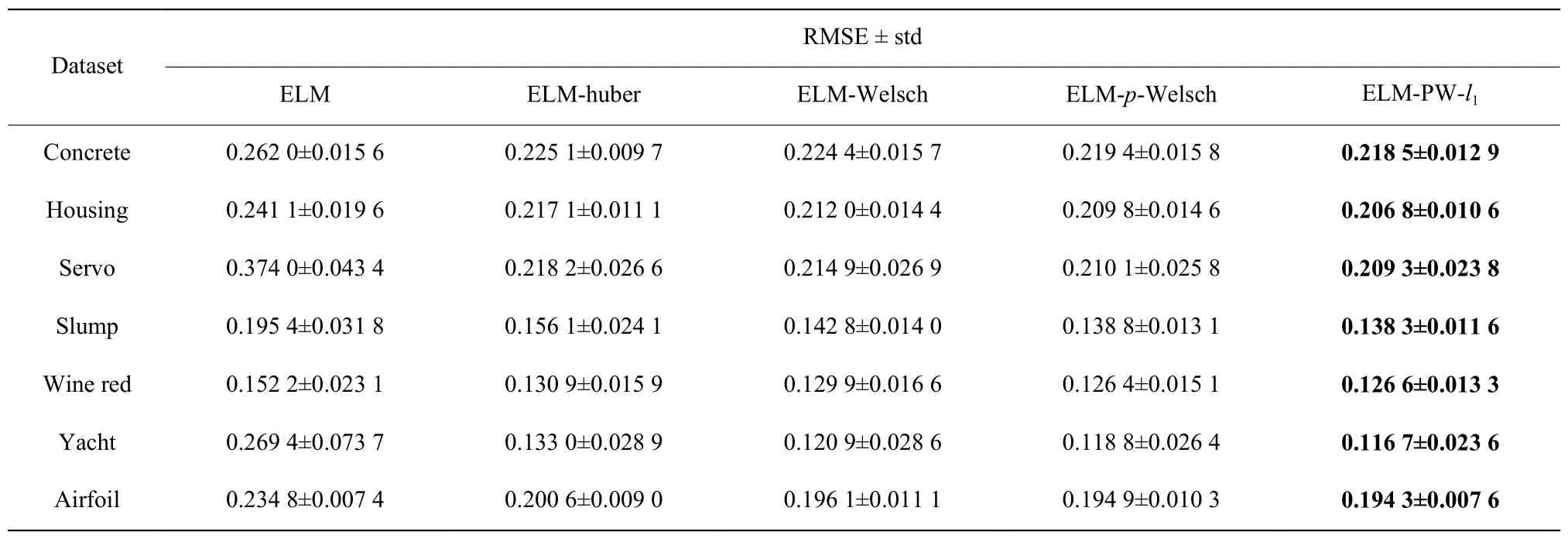
表 4 UCI回归数据集测试结果Table 4 Test results of UCI regression datasets

4 结束语

本文针对ELM在鲁棒性上的不足提出了一种 p阶Welsch损失函数，进而提出了一种基于 p 阶Welsch损失的鲁棒极限学习机。该方法使用 p 阶Welsch损失，降低了异常值数据对算法性能的影响，提升了算法的鲁棒性。在目标函数中引入 l1范数正则项，降低了模型的复杂度，提高了模型的稳定性。在极小化目标函数时采用FISTA算法提高了计算效率。通过对人工数据集和UCI回归数据集的仿真实验验证了本文算法的有效性，结果表明该算法对异常值具有更好的鲁棒性和稳定性，且算法的训练耗时更短。