汽车发动机皮带系统臂式张紧轮力学性能研究

潘 斌， 翁 涛， 杨家鹏， 安 琦

（1. 华东理工大学机械与动力工程学院，上海 200237；2. 上海贝序汽车科技有限公司，上海 201508）

目前，汽车发动机皮带系统使用的张紧轮大多是臂式自动张紧轮，当绕过张紧轮的皮带有力地变化时，张紧臂就会在弹簧的作用下摆动，实现自动张紧，因此张紧轮在工作过程中力学性能的变化十分复杂，需要深入研究。

曾祥坤等[1-2]利用力学测试仪测试出静态特性下张紧轮的扭矩与张紧臂位移之间的关系为滞回曲线，并利用最小二乘法计算出张紧轮弹簧的静刚度；同时他们利用日本鷺宫扭振试验台，建立了表征张紧器的扭矩-角位移关系的迟滞回线模型，并通过试验表征不同激振振幅和激振频率下张紧器的扭矩-角位移的关系。耿帅[3]利用AVL-EXCITE Timing Drive软件对传动系统进行研究，得出了皮带动态张力受转速及转速波动的影响比较大的结论。

张紧轮的转动角度、皮带的横向振动等受皮带动态张力变化的影响比较大。胡玉梅等[4]基于张紧装置几何模型，建立了其阻尼系数μ的数学表达式，同时研究了结构参数对张紧装置阻尼系数的影响规律，得出了影响系统阻尼系数μ的主要结构参数。田力[5]分析并提出了扭转弹簧工作状态的无接触、点接触和全接触3个阶段，提出了扭矩力的计算优化。张智[6]建立了张紧器摆角-扭矩的模型并给出了参数识别方法，建立的模型能较好地描述张紧器摆角-扭矩的迟滞特性，分析了干摩擦阻尼的大小对张紧臂的摆角幅值和带中张力波动的影响。王红云[7]通过实验测试了在不同的预载荷、激励振幅和激励频率下张紧器的扭矩、转角和两者间的相位差，分析了张紧器预载荷、激励振幅和激励频率的变化对张紧器动刚度和阻尼的影响。Zeng等[8]测量了张紧器的动态性能包括动态刚度和损耗角，测量并分析了预扭矩、激励振幅和激励频率对张紧器动态特性的影响，提出了一种用于模拟张紧器的扭矩和角位移之间关系的滞后模型。Zhu等[9]建立了考虑横向带振动的皮带轮系统干摩擦张紧器模型，研究了干摩擦对系统力学的影响。Kraver等[10]开发了一种复杂的模态程序，分析阻尼包括黏弹性带和库仑张紧器臂阻尼对张紧轮力学性能的影响。Bastien等[11]用优化的Dahl和Masing模型来预测自动张紧轮的滞回曲线，并将模型应用到张紧轮系统的力学方程中，验证了Dahl模型的可靠性。

综上所述，虽然有很多人开展了张紧轮力学性能的研究，但只考察了个别因素对张紧轮力学性能的影响，尚未形成系统研究，也无法对张紧轮的设计形成有效的理论指导。本文以汽车发动机皮带传动系统常用的臂式自动张紧轮机构为研究对象，构建力学模型，同时数值分析了该张紧轮在工作过程的力学性能，研究各种因素对其性能的影响规律，从而为该类张紧轮的设计提供理论借鉴。

1 力学建模

1.1 汽车发动机皮带传动系统

发动机皮带轮系原理如图1所示，汽车发动机皮带传动系统一般由曲轴、惰轮、水泵、发电机、压缩机以及张紧轮组成。曲轴为动力源，带动发电机、水泵和空调压缩机工作。张紧轮的作用是使皮带始终保持恒定的张力，防止皮带产生打滑。

图 1 某发动机皮带轮系原理图Fig. 1 Schematic diagram of an engine pulley system

汽车发动机在运行过程中，由于皮带所驱动的水泵、空调压缩机、发电机等工况都在不断变化，导致张紧轮的紧边和松边受到的力随机波动，当紧边的力（F1）和松边的力（F2）合力增大时，张紧轮会被向下压，产生一定角度（θ）的旋转。当F1和F2合力减小时，张紧轮会被放松，在其内部弹簧的恢复力作用下反向回转一个角度。因此，张紧轮在实际发动机工作时会不断产生往复振动[12]。

1.2 张紧轮力学分析

1.2.1 张紧轮受力及能量关系分析 在摆动过程中，臂式张紧轮各部分受到的力矩如图2所示，其中Mf1为摩擦阻尼机构产生的摩擦阻力矩；Mf2为滚动轴承产生的摩擦力矩；N为碟簧受压缩后产生的压力；M为涡卷弹簧的扭矩，顺时针方向随着θ角度的变大而变大，逆时针方向随着θ角度的变大而减小。张紧轮在初始装配时会让涡卷弹簧扭转一定的角度θ0，称为预安装角度[13]。因此张紧轮在受皮带力之前，涡卷弹簧就有一初始力矩M0。

图 2 臂式张紧轮力矩分析Fig. 2 Arm tensioner torque analysis

在进行力学分析时，首先作以下假设：（1）由于张紧轮轴承的摩擦阻力很小，皮带与张紧轮之间弹性滑动很小，故忽略皮带和张紧轮之间摩擦消耗的能量；（2）安装张紧轮的滚动轴承中的摩擦因数为定值；（3）芯轴和轴套之间的滑动摩擦很小，忽略不计。

张紧轮受力分析如图3所示，其中α是皮带的包角，R1是滚动轴承的半径，R2是皮带轮半径。张紧轮受到皮带拉力F1和F2随机变化，张紧轮臂长为L，F为F1和F2的合成力。在F1、F2和涡卷弹簧的作用下，张紧轮下压时角度为θ，回转时角度为θ′。F1和F2对芯轴中心产生的力矩为MF，其合力做功为 WF。

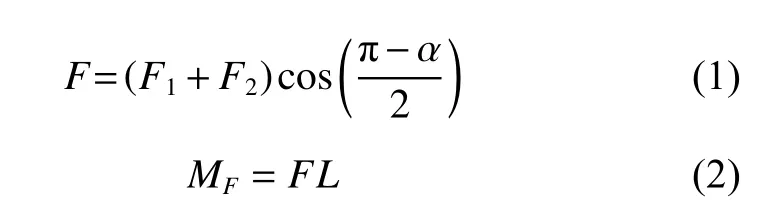
对于张紧带轮和滚动轴承所组成的系统，可以建立力矩平衡方程：

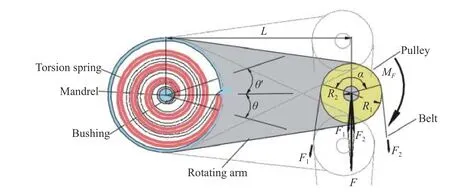
图 3 张紧轮受力分析Fig. 3 Force analysis of tension wheel

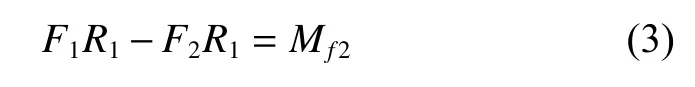
对于整个张紧轮组成的系统可以建立力矩平衡方程

在ΔM作用下，旋转臂产生加速度 ξ ，G1为张紧轮转动惯量，满足

对于张紧轮系统，根据假设分析可知，在下压过程中，张紧轮的动能主要通过以下方式消耗掉：(1) 阻尼机构在旋转过程中产生的摩擦力做功 W1；(2) 平面涡卷弹簧在缩紧时吸收的弹性势能 W2；(3) 皮带运动过程中产生的弯曲所吸收的能量 W3。因此在张紧轮下压到最大偏转角θ时，根据能量守恒定律可得到能量平衡方程

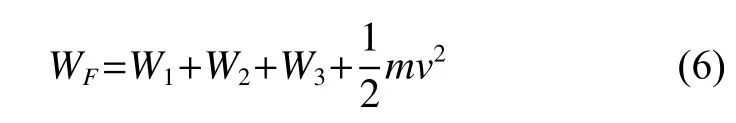
其中v是张紧轮的摆动线速度。

1.2.2 摩擦力矩及做功计算

（1）摩擦阻尼机构的摩擦力矩及做功计算

阻尼机构受力状态如图4所示，在张紧轮摆动过程中，金属摩擦片与芯轴固定不动，非金属摩擦片与张紧臂固定，随着张紧臂的摆动而发生旋转。碟簧受到挤压变形，施加给非金属摩擦片压力N，从而使摩擦阻尼机构产生摩擦阻尼。

假设芯轴半径为R0，金属摩擦片的半径为R3，阻尼机构的摩擦因数为μ1，则摩擦力矩方程为

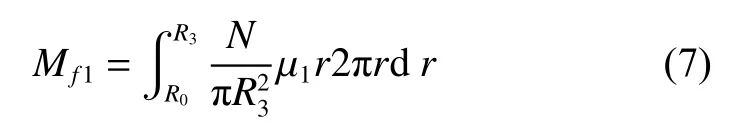
当张紧臂旋转角度为θ时，摩擦力做功为

张紧轮所用碟簧如图5所示，在压紧时提供给阻尼机构压力N，增大摩擦阻尼，张紧轮被释放时，碟簧恢复弹性形变，压力N变小。假设内径为d，外径为D，碟簧厚度为τ，压缩量为Δh，碟簧压平时的变形量为h3，K1、K4为计算系数，K4一般取1，弹性模量为 E1，泊松比为μ， C =D/d ，则N的计算公式[14]为

图 4 阻尼机构受力状态Fig. 4 Stress state of damping mechanism

其中：

（2）皮带弯曲变形吸收能量计算

皮带在接触皮带轮后发生弯曲变形。假设弹性模量为E2，惯性矩为I，发生弯曲变形的长度为l1，皮带的厚度为h2，宽度为b2，速度为v，其变形能计算公式为[15]

图 5 碟簧压缩变形Fig. 5 Disc spring compression deformation

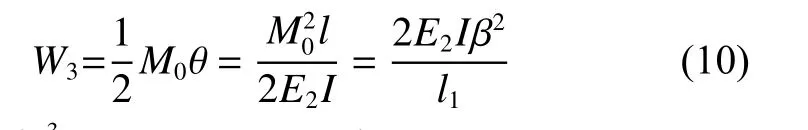
（3）平面涡卷弹簧的力矩以及弹性势能计算

假设平面涡卷弹簧的扭转刚度为G2，弹簧的宽度为b1，弹性模量为E3，厚度为h1，弹簧展开长度为k1为系数，则弹簧在旋转θ角度时的转矩公式为[16]

其中：

弹簧旋转θ角度时的弹性势能计算公式为

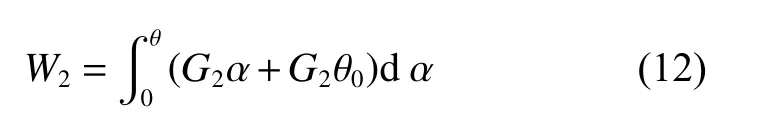
1.3 旋转臂振动计算方法

为了分析张紧轮在皮带传送过程中振动角度和皮带力关系的变化情况，采用如下方法进行计算：

（1）张紧轮在实际工作过程中，F1、F2是随机波动变化的，并且具有波动范围[17]。可以通过Matlab进行模拟，结合式（1）和式（3）计算出的F1、F2的关系，给出随机变化的F1、F2的合力F。

（2）给定初值θ=0，张紧轮初始角速度ω0=0，根据式(1)设定合力F在一定时间的变化规律和变化范围。

（3）通过离散化的思想，将时间段分割成无数个单位时间Δt，其中Δt的分割标准为：在Δt内 Δ F≤10-6。

（4）计算张紧轮旋转θ时，F1、F2所做的功WF，其计算公式为

（5）通过力矩平衡方程式(3)以及能量平衡方程式(4)和式(5),可以建立在一个Δt时间内动态力矩平衡方程和动态能量平衡方程：

（6）F1、F2不断变化时，根据式(5)，当 Δ M 不等于0时会产生相应的加速度，任意时刻的Δt都可以计算出一个加速度 ξ ，利用Euler法的改进对微分方程进行离散，并结合式(15)、式(16)对每个Δt进行迭代，进而计算出每个时刻的角度θ，得到θ关于时间t的变化规律，从而得到振动规律。离散求解的具体方式为先用Euler方法求得一个初步的近似值θp，利用θp代替后面的θn+1，最后通过求均值得到θn+1的修正。已知初始条件 θ0(t=0)=0 ，通过Matlab数值迭代计算，直到迭代到θn。

Euler法改进公式如下：

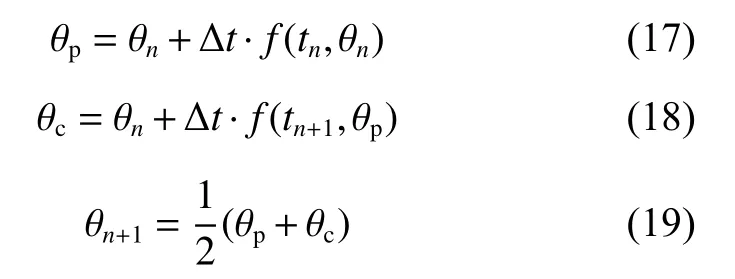
（7）通过改变张紧轮若干结构参数，观察振动曲线的变化，推断出影响张紧轮振动的因素以及这些因素的变化对张紧轮振动规律的影响，通过调节结构参数，使θ振动幅度减小。

利用Matlab编程计算，其具体过程如图6所示。

2 算例研究

以某具体的张紧轮为算例进行计算，张紧轮的主要参数见表1。

假设张紧臂受到的合力F为500～600 N，这个力是随机变化的（如图7所示），根据本文的计算方法，可以计算出张紧轮的振动规律，如图8所示。

图9所示为弹簧刚度G2为23 N·m/rad、F在500～600 N波动、L=90 mm时阻尼机构的摩擦因数μ1对张紧轮振动规律的影响。从图中可以看出，在其他条件保持不变的情况下，不同的摩擦因数振动规律大致相同，摩擦因数越大时旋转臂的振幅越小。

图10所示为弹簧刚度G2为23 N·m/rad、摩擦因数μ1=0.3、L=90 mm时，F对张紧轮振动规律的影响。从图中曲线可以看出，在其他条件保持不变的情况下，F的波动范围越大，张紧轮的振幅越大。

图11所示为摩擦因数μ1=0.3、F在500～600 N波动、L=90 mm时弹簧的刚度G2对张紧轮振动规律的影响。从曲线中可以看出，在其他条件保持不变的情况下，弹簧的扭转刚度G2对张紧轮振动的影响很大，G2增大，张紧轮的振幅明显增大。

图 6 计算流程图Fig. 6 Calculation flow chart

表 1 张紧轮实验参数Table 1 Experimental parameters of tension wheel

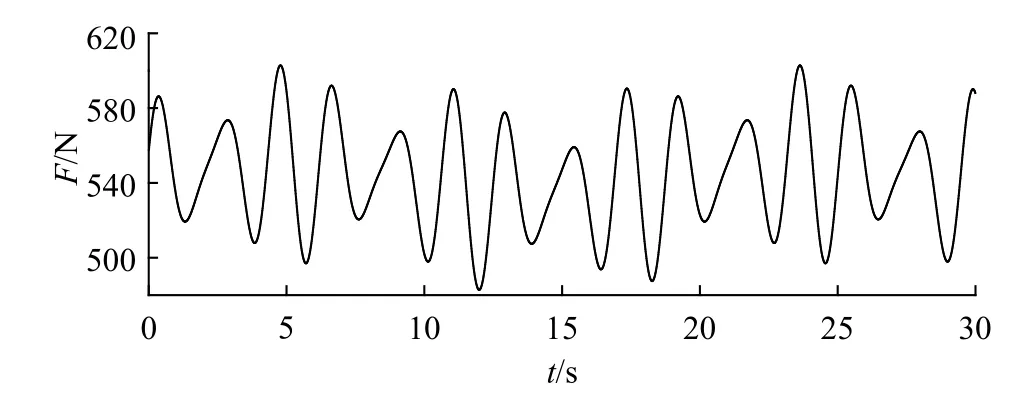
图 7 F的随机波动规律Fig. 7 Stochastic wave curve of F

图 8 张紧轮的振动规律Fig. 8 Vibration curve of tensioner

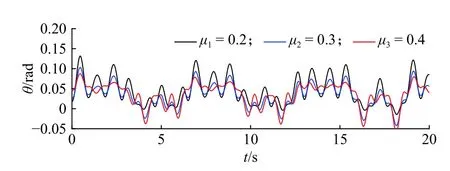
图 9 阻尼结构的摩擦因数对振动规律的影响Fig. 9 Influences of friction coefficient of damping structure on vibration

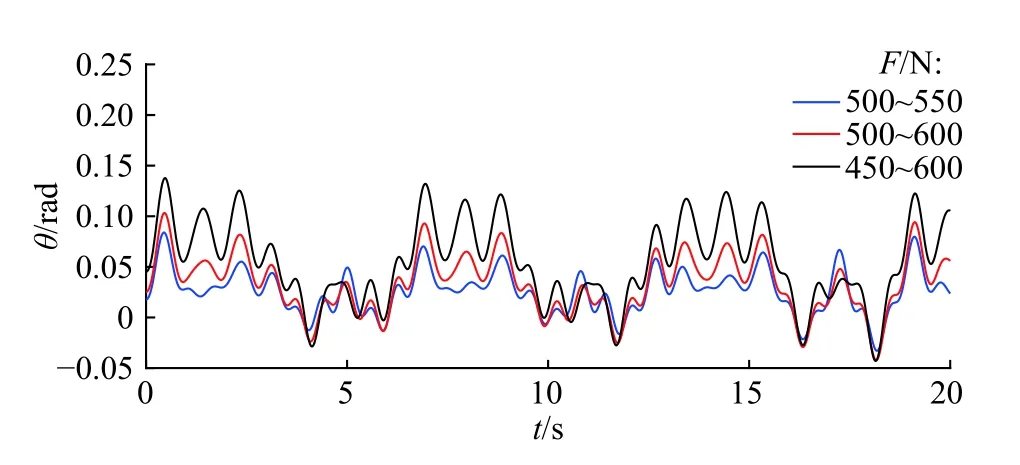
图 10 F的波动范围对振动规律的影响Fig. 10 Influences of the fluctuation range of F on vibration

图12所示为弹簧刚度G2为23 N·m/rad，摩擦因数μ1=0.3，F在500～600 N波动时，L的大小对于张紧轮振动规律的影响。从曲线中可以看出，在其他条件保持不变的情况下，臂长L越大，张紧轮的振动幅度越大。

图 11 弹簧的刚度G2对振动规律的影响Fig. 11 Influences of spring stiffness G2 on vibration

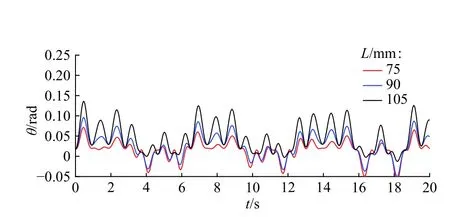
图 12 臂长L对振动规律的影响Fig. 12 Influences of arm length L on vibration

3 结 论

（1）以汽车发动机张紧轮为研究对象进行力学分析，建立了动态力矩平衡方程和动态能量平衡方程，并对模型中力矩和做功建立了计算模型。同时建立了能量和力矩的实时动态平衡方程，采用数值计算方法对模型进行了求解，实现了对张紧轮张紧过程中旋转臂振动性能的计算。

（2）以某一个具体的张紧轮机构进行算例研究，考察了弹簧刚度、阻尼机构的摩擦因数、臂长以及随机变化的皮带拉力对张紧轮振动性能的影响。研究表明，在其他参数不变的情况下，随着弹簧刚度的增大，张紧轮的摆动角度变化变小，并且只要弹簧刚度有一个很小的变化，就会引起旋转臂的振幅发生明显变化。阻尼机构的摩擦因数对于旋转臂的振动影响同样很大，摩擦因数增大，张紧轮的振动幅度将变小。张紧轮受力的波动范围增大，张紧轮的振幅变大。旋转臂的臂长增大，张紧轮的振幅将增大。