多自主车辆队列跟随控制器设计

杨 祺， 刘士荣

（杭州电子科技大学自动化学院，杭州 310018）

随着机动车保有量的日益增加，交通拥堵、交通事故及能源环境的矛盾进一步激化，作为解决此矛盾的重要手段之一，智能交通系统的研究日益迫切。自主车队系统作为该系统的重要子系统，其目的是通过传感、通信以及控制技术使多自主车辆在领头车辆的带领下以车队的形式行驶，队列则是自主车队系统中最常见的队形。自主车队内车辆保持合理的行车间距行驶，不仅可以大幅度提高车辆密度，增加道路的车流量，还能够减小风阻对车辆的影响，从而降低油耗[1]。自主车辆以队列形式进行运输也可在危险、重复程度高的场景中代替人类驾驶员，如在矿山开采、物流运输等运输场景中可实现24 h不间断运输。

多自主车辆队列跟随控制重在环境感知与控制器设计的研究，而控制器的设计往往依赖于周围环境信息的获取，因此能够准确地获取周围的环境信息是自主车辆队列控制的前提条件。在环境感知研究中，文献[2-3]利用视觉信息中丰富的障碍物特征纹理信息从中识别出不同的障碍物，但该方法受光线与相机抖动的影响较大。Maral等[4]、Olmeda等[5]分别提出了用双目相机和红外相机来克服此缺陷，但检测视野和检测范围较小。毫米波雷达在纵向方向检测距离较长且精度较高[6]，但对目标横向运动数据不精确，导致其感知范围狭隘。激光雷达具有精度高、几乎不受光照影响的优点，目前广泛应用于自主车辆的环境感知领域。

在控制器设计方面，Marino等[7]采用嵌套PID控制方法，将一个PID控制器嵌套进另一个PID控制结构中，虽然比单个PID控制器提高了精度，但也增加了需要调节的参数数量。Wang等[8]利用多个模糊控制器对自主车辆的角速度进行控制，有效地减小了角度误差。文献[9]针对含扰动的多智能体系统，设计了基于双不变集的事件触发分布式预测控制策略。

在上述环境感知方面的研究中，以单一车载传感器的研究为主，自主车辆的环境感知能力不可避免地会受到每一种传感器缺点的制约。在上述控制器设计的研究中，主要针对通信正常或无通信的情况进行研究，缺少对通信回路在正常情况下突然中断情况的讨论。为解决这些问题，本文采用激光与视觉传感器作为感知周围环境信息的车载传感器，分别采用激光测距和视觉传感器提取环境信息并将两种传感器数据进行融合。针对自主车队内车辆间是否有通信，分别设计了常规和应急两种控制器，并在ROS平台上进行了仿真，仿真结果表明所设计的自主车辆队列控制器无论在通信正常还是通信中断时均可以实现自主车辆队列安全行驶。

1 基于虚拟结构的领航-跟随策略

自主车辆编队控制问题的研究来源于多机器人任务规划及协作问题的研究，本文采用两轮差分移动机器人作为研究对象，并采用基于虚拟结构的领航-跟随法作为跟随策略。

1.1 运动学模型

两轮差分移动机器人拥有两个标准驱动轮和一个无动力的小脚轮，配备激光、单目相机等传感器设备，可用里程计计算出自身姿态位置。如图1所示，机器人将自身作为局部坐标系的原点建立局部坐标系。每个机器人在全局坐标系下的位姿可表示为

其中： i 为机器人的编号； xi和 yi分别表示机器人在笛卡尔坐标系 x 轴和 y 轴方向上的位置； θi表示机器人当前前进方向与 x 轴正方向的夹角。第 i 个机器人在 x 、 y 轴方向上的线速度及角速度可表示为，和，因此有

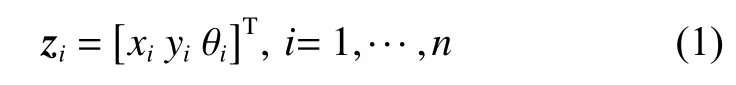
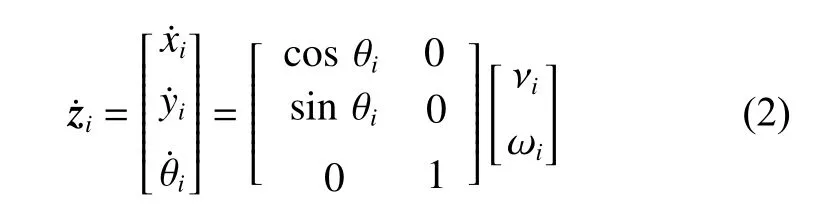
其中： vi表示第 i 个机器人的线速度； ωi表示第 i 个机器人的角速度。

机器人线速度和角速度与两个差分轮旋转速度的关系可以表示为

其中： r 为差分驱动轮的半径； d 为两个驱动轮之间的距离。差分驱动轮旋转速度与机器人线速度及角速度的关系为

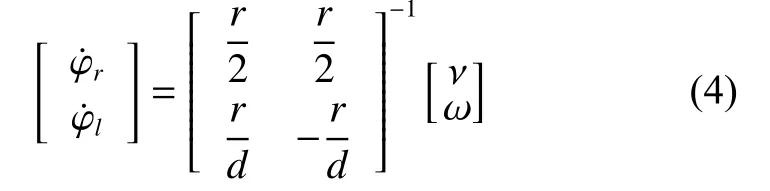
联合式（2）、式（3）可以得到典型的差分驱动机器人运动学模型：

图 1 机器人坐标系示意图Fig. 1 Schematic diagram of robot coordinate system

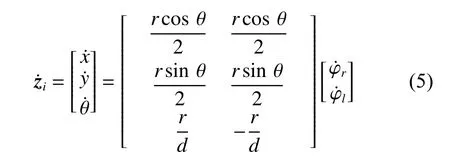
1.2 基于虚拟结构的领航-跟随策略

领航-跟随法主要分为l-l方式和l-φ方式[10]，本文采用l-φ领航-跟随法作为编队控制策略，即自主车辆将前车作为领航车辆，通过保持与前车之间的相对距离和相对角度使队形达到稳定，并在l-φ控制策略基础上引入了虚拟机器人的概念。自主车辆通过转换矩阵求出虚拟机器人位姿，并调整自身的速度来逼近在刚体中相对应的虚拟节点，确保二者之间的位置和方向误差无限趋近于零。

图2示出了领航者机器人、虚拟机器人和跟随机器人之间的关系。在保持既定队形时，虚拟机器人的位姿将和领航者保持着一个固定的变换关系：

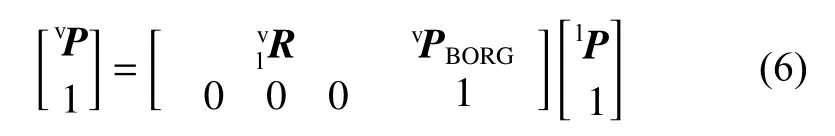
其中：lP 、vP 分别表示领航机器人和虚拟机器人的位姿；表示从领航机器人姿态映射到虚拟机器人姿态的旋转矩阵；vPBORG表示虚拟机器人和领航机器人之间坐标偏移矢量。

图 2 领航机器人，虚拟机器人和跟随机器人的关系示意图Fig. 2 Schematic diagram of leader robat, virtual robot and follower robot

2 基于激光和视觉传感器的环境信息感知

多自主车辆队列的行驶环境复杂多变，使得它必须具备感知周围环境的能力，包括领航车辆的位姿、障碍物位置等。当通信正常时，可通过通信获取部分信息；当通信中断时，需要通过车载传感器感知周围环境。本文选用激光和视觉传感器作为自主车辆的车载传感器，通过信息融合的方式从激光和视觉数据中获取控制器所需要的领航车辆相对位置信息。

2.1 基于激光传感器的环境信息提取

选用激光传感器作为主要车载传感器之一，利用了激光传感器实时性好、探测范围广、在夜间与在白天的效果相差无几等优点。基于激光传感器提取环境信息的步骤如下：

（1）对激光数据进行筛选。本文只考虑影响车辆行驶的障碍物，因此只保留高度与车身相似的障碍物信息。

（2）采用DBSCAN[11]算法对障碍物数据进行聚类。该算法是一种基于空间密度的数据聚类方法，允许使用索引结构进行密度估计，因此数据集可以拓展至大型数据库[12]，适合处理数据量庞大的激光测距传感器数据。

（3）求取各聚类点集的凸包，即求能够包络点集中所有点的最小凸多边形。

（4）求各凸包的最小外接矩形。不同点集获取的凸包结构不同，很难对所有点集进行统一分析。本文采用旋转卡壳法[13]求凸包的最小外接矩形，用该矩形拟合障碍物的物理形状，并将矩形的中心作为障碍物所在位置，记为 Cl(xl,yl) 。

2.2 基于视觉传感器的环境信息提取

激光信息可以获取周围障碍物的物理特征及与自身的相对距离，但无法分辨出哪个障碍物是领航车辆。采用Camshift算法[14]通过视觉搜索、跟踪领航车辆，并将搜索框中心作为搜索到前车的所在位置。当目标区域的尺度发生变化时，该算法能够自适应调整窗口大小继续跟踪。算法步骤如下：

（1）在初始帧中选择包含领航车辆的目标区域，对搜索窗口进行初始化；

（2）对初始帧中的目标区域进行颜色直方图统计；

（3）若当前帧图像不为空，计算它的颜色概率分布图（即反向投影图）；

（4）根据反向投影图和搜索窗口，调用Meanshift算法，得到收敛窗口；Cc(xc,yc) ，作为前车的中心点；

（5）Camshift算法通过Meanshift迭代得到的收敛窗口所反映的跟踪目标信息对下一帧目标搜索的窗口大小进行调整，并将该收敛窗口的中心记为

（6）在下一帧图像中，用步骤（5）得到的收敛窗口作为搜索窗口，并跳转到步骤（3）继续执行。

2.3 视觉与激光传感器的信息融合

自主车辆行驶时需要不断感知周围环境中的障碍物，用 o bj(l,θ) 表示障碍物信息， l 和 θ 分别表示自主车辆与障碍物之间的相对距离和角度， Cl(xl,yl) 为激光数据聚类结果的最小外接矩形中心点，将该点到自主车辆的距离作为障碍物与自主车辆之间的相对 距离 l 。

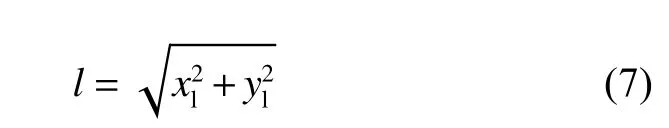
同样，可求该点 Cl(xl,yl) 在自主车辆局部坐标系下 的角度，记作 θl。

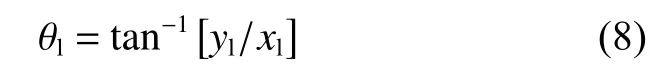
自主车辆在跟随领航车辆行驶时，需要通过车载传感器获取领航车辆的相对位置。通过式（7）和式（8）可以获得周围障碍物与自主车辆的相对位置，但此时自主车辆无法知道哪一个障碍物是领航车辆。

通过Camshift算法在当前帧中找到领航车辆，领航车辆的中心点坐标为 Cc(xc,yc) ，该点以像素为单位，需转换成自主车辆局部坐标系中的相对角度信息。图像平面坐标系与自主车辆局部坐标系之间的关系如图3所示，其中 xroryr为自主车辆所在坐标系， yc是投影在图像坐标系中领航车辆的中心点，wimage是目标中心点投影在图像平面的宽度，即该图像平面中边缘到中心点沿着 y 坐标系方向的像素个数， θfov是相机的成像角度。由式（9）可求得领航车辆在当前帧中的坐标点转换成自主车辆局部坐标系中的相对角度：

通过式（10）在 n 个障碍物中找到偏离角度与 θ最接近的障碍物的角度：

其中： θli为激光数据中第 i 个障碍物的相对角度信息； n 为当前环境中障碍物数目。偏离角度为 θobj的障碍物即为领航车辆。

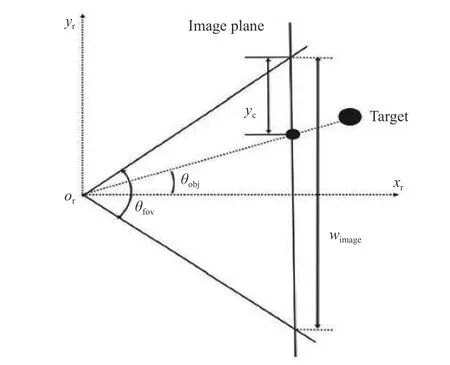
图 3 图像平面坐标系与自主车辆局部坐标转换关系Fig. 3 Transformation relationship between image plane coordinate and local coordinate system of autonomous vehicles

3 自主车辆跟随控制器设计

3.1 基于李雅普诺夫稳定性的跟随控制器设计

自主车辆可以通过自身搭载的GPS传感器获取自身所在位置的全局坐标信息，并通过惯性传感器、磁罗盘等车载传感器获取自身朝向角度信息。当车队成员之间通信正常时，跟随车辆可通过通信获得前车的位姿信息，并通过式（6）计算虚拟车辆位姿信息。将跟随车辆与虚拟车辆的位姿信息分别用(xf,yf,θf) 和 ( xv,yv,θv) 表 示，建 立 如 图4所 示 误 差 模型，用 e 表示位姿误差，通过几何原理，可以得出以下关系：

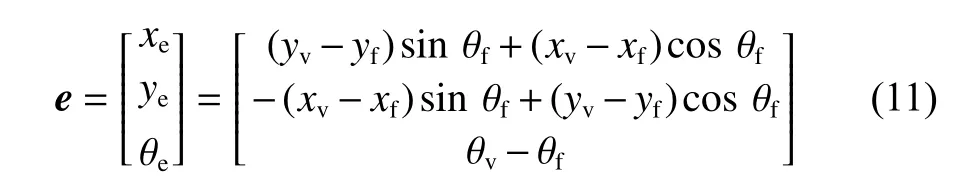
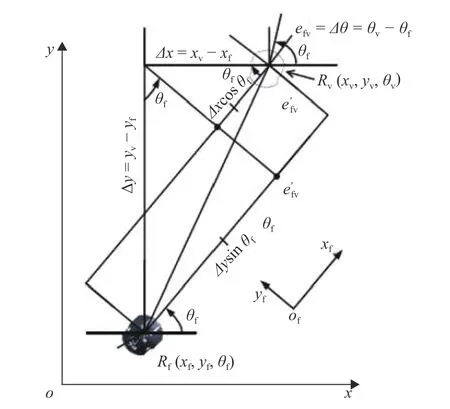
图 4 跟随车辆与虚拟车辆的位姿关系Fig. 4 Posture relation between follower and virtual vehicle

将跟随车辆和领航车辆的速度分解到 x 轴和 y轴方向可得

队列保持稳定跟随的条件为

式中： δ 为误差常数； δP表示位置误差常数； δo表示姿态角误差常数，表示误差在一个有限时间 T 内趋近 于误差常数。对误差模型 e 求导可得

式 中： vf和 vv分 别 表示跟随 车 辆 和虚拟车 辆 的 线速度； ωf和 ωv分别表示跟随车辆和虚拟车辆的角速度。选用的控制率为

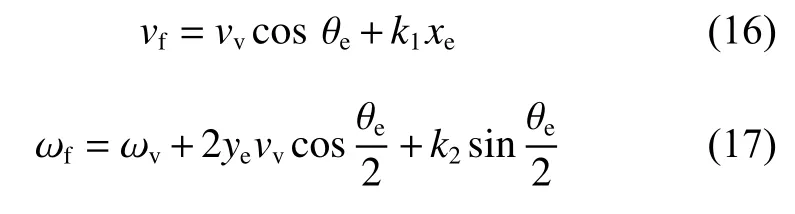
其中： k1、 k2为正系数。为证明其稳定性，本文选取李雅普诺夫函数为

可 知 此 时 V ≥0 ，当 且 仅 当 xe=ye=0 ， θe=0 时，V =0 。对式（18）求导可得

将式（15）代入式（19）可得

将式（16）和式（17）代入式（20）得

可知 当且仅当 ， 时， ，故系统渐近稳定。

3.2 基于模糊控制的跟随控制器设计

当车辆间无通信时，车辆仍可通过车载传感器获取自身位姿信息，但跟随车辆无法获得前车的位姿信息，无法计算朝向角误差 θe，故无法使用3.1节设计的控制器。此时跟随车辆将式（9）所得相对角度作为与前车的偏离角度，并结合式（10）在激光数据聚类结果中找到与前车匹配的障碍物信息，将式（7）所得各个障碍物的相对距离信息作为跟随车辆与领航车辆之间的相对距离记为 l 。根据图5所示前后车辆 位姿关系，可得到位姿误差如下：

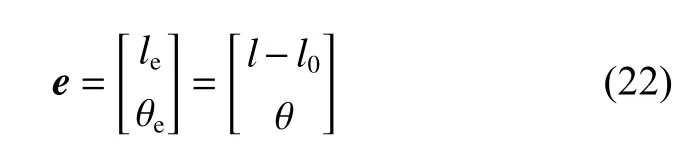
式中： le和 θe分别表示距离误差和角度误差； l0为跟随车辆与领航车辆之间需要保持的相对距离。

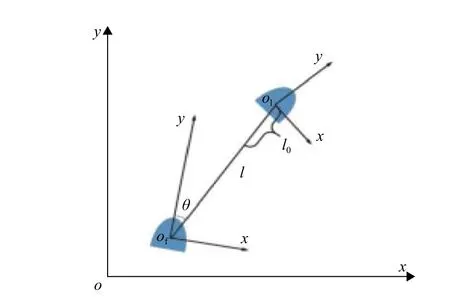
图 5 领航车辆与跟随车辆的位姿关系Fig. 5 Posture relation between leader and follower

在此引入模糊控制器对自主车辆进行控制，将 le和 θe作为 模 糊 控 制 的 输 入，将 跟 随车辆的速度 ν 和角速度 ω 作为输出。

输入、输出的模糊集划分如表1和表2所示，其中输入 le、 θe的论域分别取[0, 3 m]、 [ -π/2,π/2] ，输出 ν 、 ω 的 论 域 分 别 取 [ 0m/s,3m/s] 、 [-0.2rad/s,0.2rad/s] 。

表 1 输入变量模糊集划分Table 1 Partition table of input variable fuzzy sets

表 2 输出变量模糊集划分Table 2 Partition table of output variable fuzzy sets

采用图6所示隶属度函数对两个输入变量进行模糊化。由于真实路况中实际误差无法为0，因此将图6（a）、6（b）两个输入模糊集中的ZE函数分别设为z形函数和梯形函数，表示系统在误差允许范围内保持稳定行驶，避免了由于较小的误差导致自主车辆不停地调整位姿影响乘客舒适感。当误差较大时，自主车辆需要快速地调整速度，图6（a）中的VF和图6（b）图中的NL、PL所占比重需要快速增大，故将图6（a）的VF函数和图6（b）的NL选用s形隶属度函数，将图6（b）的PL选用z形隶属度函数。

图 6 输入变量模糊隶属函数Fig. 6 Fuzzy membership function of input variables

采用图7所示隶属度函数对两个输出变量进行模糊化。为了使输出更平稳、连贯，采用高斯隶属度函数作为两个输出变量的隶属度函数。模糊控制的规则表往往由经验丰富的专家给出，用来反映输入到输出的隶属度关系。本文模糊控制的核心是当 le过大或过小时，模糊控制器可以输出一个较大或较小的 ν ；当 θe过大或过小时，模糊控制器输出一个较大或较小的 ω 来保证自主车辆在此控制器下能够稳定跟随在虚拟位姿的位置。采用2个输入、2个输出、6个模糊级别分别对 ν 和 ω 进行模糊控制，模糊规则形式如下：

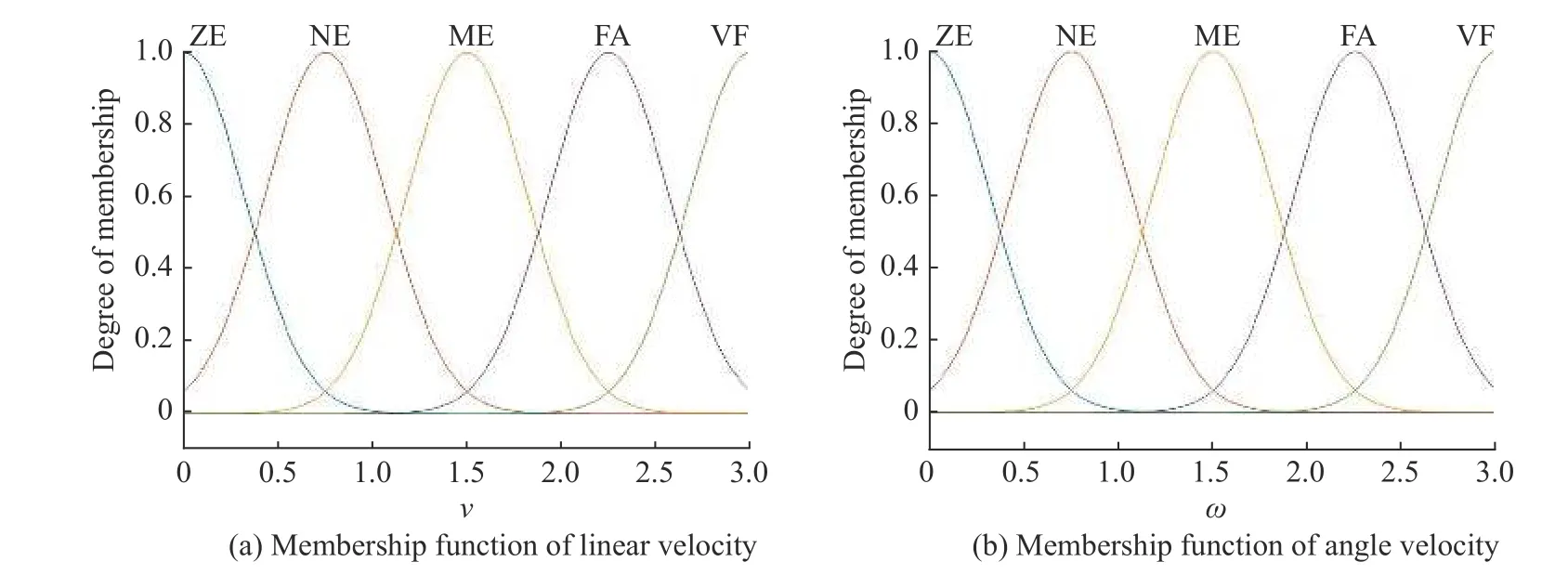
图 7 输出变量模糊隶属函数Fig. 7 Fuzzy membership functions of output variables

输出变量 ν 的模糊规则形式

输出变量 ω 的模糊规则形式

采用重心法使输出结果去模糊化:

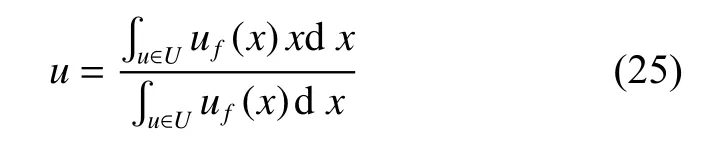
值得注意的是，在跟随车辆与前车之间无通信的情况下，本文设计的控制器是短时间内使用的备用控制器，无法保证长时间的安全行驶。一旦周围的其他车辆进入到跟随车辆与前车之间，跟随车辆将完全丢失前车信息。因此若在一定时间内未恢复通信，则跟随车辆需离开道路，停靠在安全区域等待维修。

4 仿真实验

为了验证两种控制器的有效性和稳定性，在ROS indigo版本和GAZEBO 7.0版本中采用3辆P3DX移动机器人作为仿真对象进行仿真实验。选用的二维激光测距传感器的扫描范围为 - 180°～180°，角度分辨 率 为 0 .5°，选 用 的 相 机 分 辨 率 为 6 40×480 。式（16）、式（17）中控制器参数 k1=1.5 ， k2=0.4 。

实验中，领航车辆的控制率由式（24）给出，模拟自主车队变车道的过程。该过程中线速度、角速度均发生变化，是实际驾驶情况中较复杂的一种。3辆车的初始位置分别为（0，0）、（0，-2）、（0，-4），朝向角均为90°，即朝向y轴正方向。

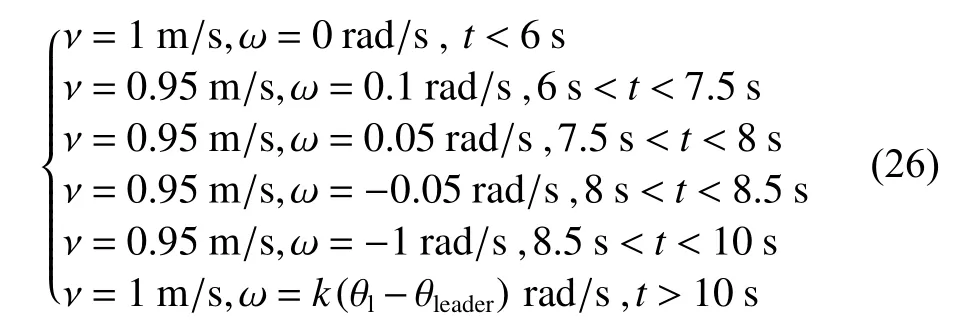
图8所示为两种控制器自主车队变车道的轨迹图。可以看出，在领航车辆变道时，跟随车辆均可以较好地跟随。

图9所示为两种控制器3辆自主车辆的线速度变化曲线。可以看出，两种控制器都能很好地使跟随车辆的速度趋近于领航车辆，且基于李雅普诺夫法设计的控制器可以使速度变化更为平缓，但收敛时间要长于模糊控制器。

图10所示为两种控制器3辆自主车辆的角速度变化曲线。可以看出，两种控制器都可以使角速度很好地收敛。

图11示出了李雅普诺夫法控制器误差模型中误 差 xe和 模 糊 控 制 器 误 差 模 型 中 de的 变 化 曲 线，图12示出了李雅普诺夫法控制器误差模型中误差 ye和模糊控制器误差模型中 θe的变化曲线，可以看出两种控制器的误差均能收敛到误差范围之内。

图 8 两种控制器的轨迹图Fig. 8 Trajectory diagrams of two controllers

图 9 两种控制器线速度图Fig. 9 Velocity diagrams of two controllers

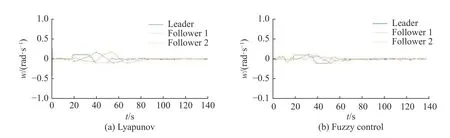
图 10 两种控制器的角速度图Fig. 10 Angular velocity diagrams of two controllers

xe de图 11 李雅普诺夫法控制器误差 （a）和模糊法控制器误差 （b）xe deFig. 11 Error of Lyapunov controller (a)and error of the fuzzy controller(b)

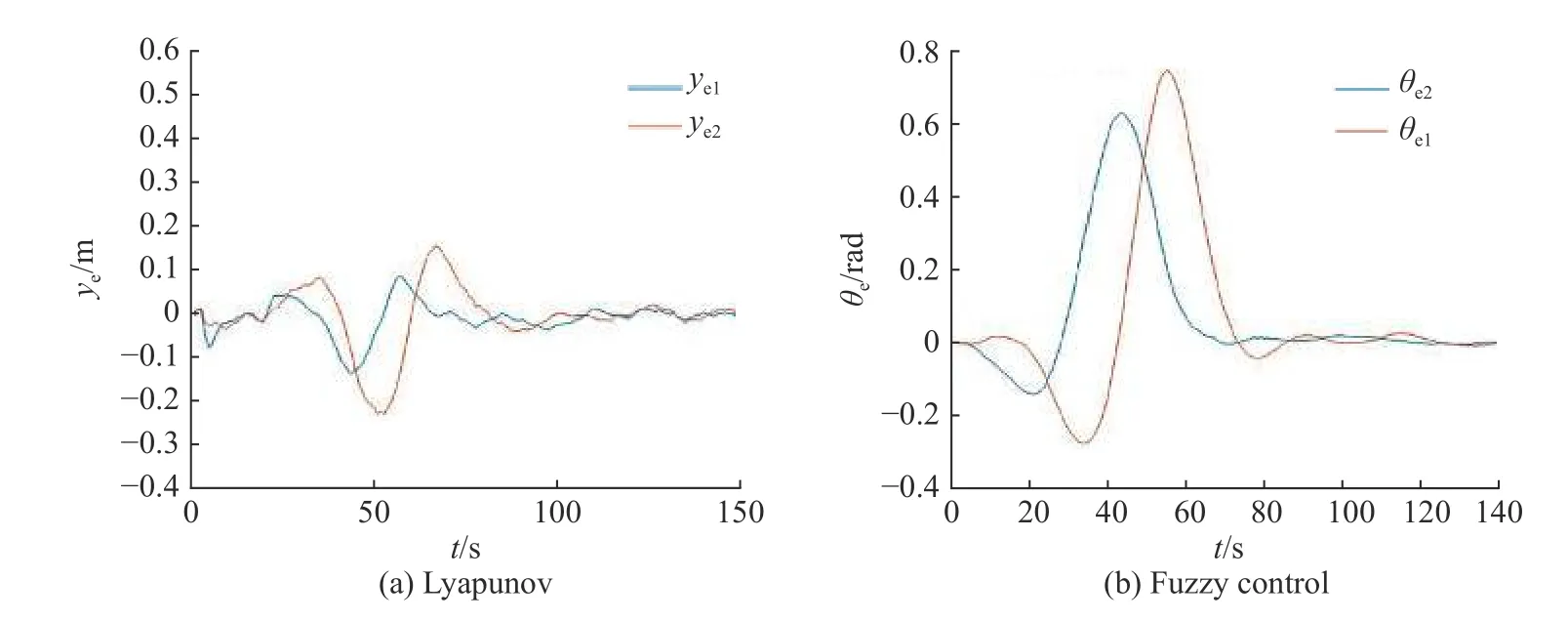
ye θe图 12 李雅普诺夫法控制器误差 （a）和模糊法控制器误差 （b）ye θeFig. 12 Error of Lyapunov controller (a) and Error of fuzzy controller (b)

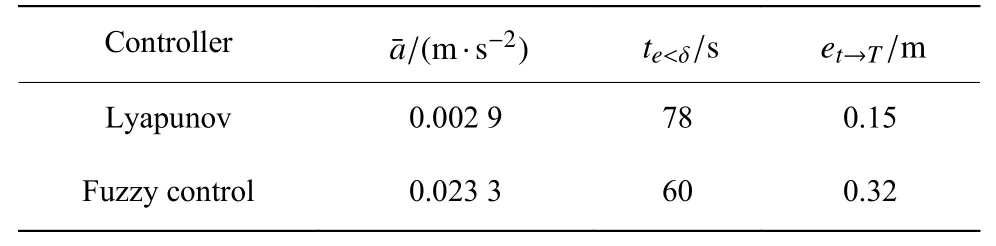
表 3 各项评价指标Table 3 Table of evaluation indicators

5 结论与展望

采用激光测距和视觉传感器作为感知周围环境的车载传感器，通过信息融合的方式获取领航车辆位置信息，有效地弥补了单一传感器存在的缺陷。分别提出了基于李雅普诺夫稳定性和模糊控制策略在通信正常和无通信两种情况下的控制器设计，有效地解决了自主车队成员间通信回路中断的问题，提升了自主车队系统对通信回路的鲁棒性，并通过仿真实验证明了本文设计的自主车辆队列跟随控制器的稳定性和有效性。

目前在多自主车辆队列控制中，仍有诸多方面值得深入学习和研究，例如，在自主车队列避撞方面，在行驶过程中，应充分考虑其他交通参与者对车队带来的影响，避免可能发生的碰撞；在自主车队队列重构方面，在自主车队列行驶时，存在队内成员需要离开车队或是其他自主车辆需加入车队，因此需要队列优化重构策略对成员入队/出队进行控制。