基于逆向学习行为粒子群算法的云计算大规模任务调度

赖兆林， 冯 翔， 虞慧群

（华东理工大学计算机科学与工程系，上海 200237）

云计算是一种新的计算模型和服务模式[1]，融合了网络及计算机技术，实现资源共享和按需访问，并为基础设施、平台和软件(应用)服务。当用户应用程序需要服务时，它可动态地提供尽可能多的计算资源。与此同时，应用程序可以选择其数据存储在哪些服务器上，使得用户能更好地掌控自己的数据。云计算的原理是以网络的方式将较大的计算程序拆分成一系列小的子程序，然后通过服务器集群计算后的结果传给用户[2]。例如Google的Map/Reduce框架就是采用这种技术，TB级的数据可在数秒内被处理完成，从而实现了与超级计算机同样功效的服务[3]。

在商业应用中，可采用离线方式的有数据挖掘和数据存储等，而对于实时性要求较高的应用，例如交易处理及电子商务，都要求系统尽可能在较短时间内处理完提交的任务。然而，通常情况下，用户所请求的服务数量比较大，因此，为了使系统能快速响应用户请求，任务调度算法起着至关重要的作用。与此同时，设计有效的调度算法，使得整个系统达到最优，成为云计算研究的难点[4]。

云计算中的任务调度问题属于NP完全问题[5]。智能优化算法很适合求解此类问题[6]，例如遗传算法（GA）、蚁群优化(ACO)算法、粒子群优化(PSO)算法和布谷鸟搜索算法(CSA)等，且这些算法已被应用于解决云计算任务调度问题，并取得一定的效果。文献[7]采用GA算法实现了云计算中独立任务的有效调度。文献[8]利用ACO算法优化了云计算的总任务及平均任务完成时间；文献[9]提出了基于PSO的调度算法，使得云计算任务的处理时间及传输时间最小；文献[10]使用布谷鸟搜索算法对云计算任务的总响应时间进行了优化。任何优化算法都有其优点和不足。例如，GA算法的时间开销小及鲁棒性高，而不足之处是容易陷入早熟收敛[11]；ACO算法具有较好的搜索能力，但计算量大，收敛速度慢[12]；PSO算法实现容易、需要设置的参数少及收敛速度快，但迭代后期局部寻优性能不足[13]；CSA算法计算速度快，但存在全局寻优性能与局部寻优性能不平衡的缺陷[14]。

智能优化算法的共同特征在于模拟自然行为，且每一个算法都具有其优缺点[15]。此外，文献[15]指出不存在任何一个算法可以解决所有的优化问题，某一算法可能在某些问题上表现出色，但是在另一问题上其性能不佳。因此，为了提升智能优化算法的优化性能，一些研究者提出了新的优化算法。Li等[16]受动物迁徙行为启发，提出了动物迁徙优化(BBO)算法；Zhang等[17]通过模拟自然界中植物根系生长行为，提出了根生算法(RGA)；Feng 等[18]以社会群理论为基础，提出了社会群熵优化(SGEO)算法。还有一些学者通过改进已有算法来提升优化算法的性能。Zhan等[19]在PSO算法基础上采用正交学习策略，提出了正交学习粒子群(OLPSO)算法；Chen等[20]把衰老机制引入PSO算法中，提出了老化领导者的PSO(ALC-PSO)算法；Qin等[21]基于PSO引入群内交互学习策略，提出了群内交互学习PSO (IILPSO)算法。PSO算法作为较为经典的智能优化算法，最近几年依然有不少学者对其进行研究并改进。Dong等[22]受机器学习中的监督学习和控制领域中的预测控制策略启发，提出了一种基于监督学习控制的自适应粒子群优化(APSO-SLC)算法；Gong等[23]通过采用遗传算子来生成粒子学习的范例，提出了一种遗传学习粒子群(GL-PSO)算法；Lin等[24]通过设计一种平衡适应度估计方法和一种新的粒子速度更新公式，提出了一种新的多目标粒子群优化(NMPSO)算法。

本文受文献[25]中生物以性别分群及文献[26]中蜜蜂逆向学习行为的启发，提出了一种逆向学习行为粒子群优化(RLPSO)算法，并应用到云计算任务调度问题上。该算法在传统粒子群算法基础上，首先把整个种群划分为雄性群体和雌性群体，然后引入逆向学习行为。这两种机制有助于提升算法搜索能力，并且可以加快算法收敛速度。在云计算任务调度问题上，与4个经典的智能优化算法相比，RLPSO算法在大规模任务调度时，总任务时间减少，并且提升了任务调度效率。

1 云计算调度问题模型化

粒子的编码主要有两种方式，一种是直接编码(即一个粒子代表一个可行解)；另一种是间接编码(即一个粒子表示一种任务调度策略), 本文使用间接编码。

假设云计算下的任务数为Tn，资源数为Rn，子任务总数为Sn。由于每个任务划分为多个子任务，从而有子任务的总数大于任务数。子任务数与每个任务数的关系如式(1)所示：

其中，Hn(i)表示第i个任务包含子任务的数目。

使用顺序法对子任务进行编码，其公式如下：

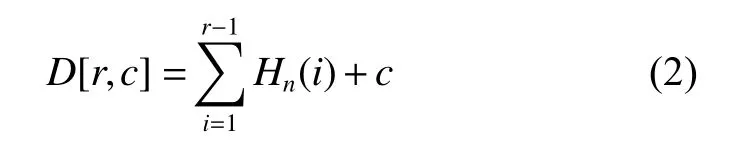
其中，D[r, c]表示第c个任务中的第r个子任务。

假设Tn=3，Rn=3，Sn=10，并且粒子(2, 1, 3, 1, 3, 1,2, 1, 3, 2)是可行的调度，图1示出了粒子编码及解码示意图。对于编码过程，其任务、子任务对(2, 6)表示第2个任务的第3个子任务编号为6；子任务、资源对(6, 1)表示把子任务6分配给资源1执行。对于解码过程，资源1上执行的子任务是{2, 4, 6, 8}，资源2上执行的子任务是{1, 7, 10}，资源3上执行的子任务是{3, 5, 9}。

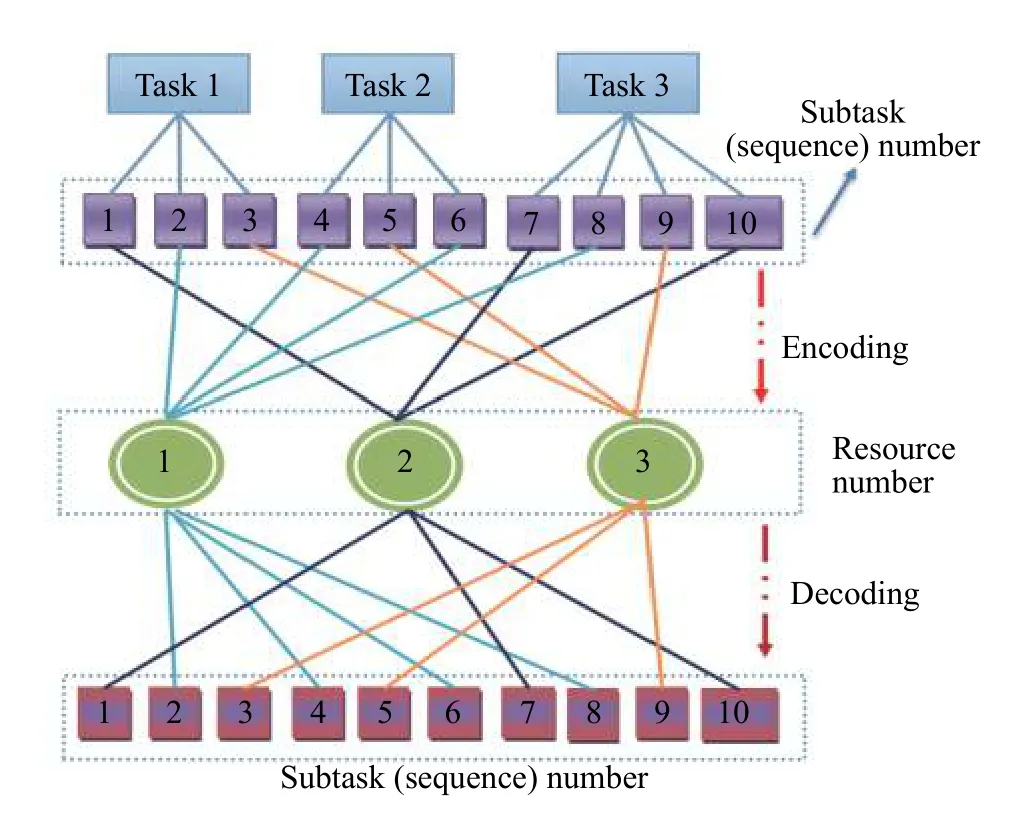
图 1 粒子编码解码示例图Fig. 1 Example of particle coding and decoding

完成全部任务的总时间如下：

其中：Utime(k, i)表示第k个资源执行第i个子任务所需的时间开销；m表示分配给该资源的子任务数目。

从式(3)可知，完成一组任务的可行调度总时间为Otime，由于一组任务的可行调度对应于优化算法中的一个解xi(粒子), 因此，完成全部任务的总时间转换为优化问题的目标函数为

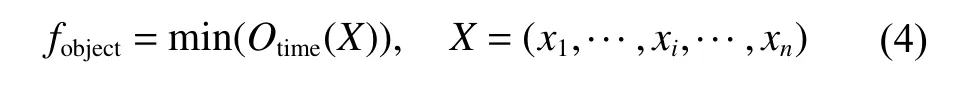
2 改进的粒子群算法

2.1 PSO算法

PSO算法[27]是研究者受鸟群的集体行为启发提出的一种自然启发式算法。该算法模拟了自然界中鸟群捕食行为，从而建立具有群体智能的简单模型。整个群体中的个体共享最优个体信息，其他个体往最优个体方向移动，使得种群逐步趋于最优。

PSO算法把待优化的目标函数的解看作是搜索空间里的一个粒子，在搜索过程中，通过适应值来评价个体的优劣。每个个体的位置更新由其速度和距离决定。初始状态下，PSO中的个体随机分布在搜索空间内，通过迭代的方式搜索最优解。每次迭代时，个体在更新自己的位置之前，获取群体当前最优个体位置及本身历史最优位置，以此调整自己的飞行方向。随着迭代次数的增加，群体内的其他个体逐渐接近最优个体。当达到终止条件时，整个算法停止搜索，此时，群体内最优个体位置即是该算法得到的最优解。个体位置更新公式如下:

其中： xk(t) 为个体k在第t次迭代时的位置；Vk(t)为该个体的速度；pk(t)为个体k搜索到的局部最优位置；G(t)为全局最优位置；w为惯性权重；c1和c2表示加速常数；r1和r2表示[0, 1]范围的均匀随机数[28]。

2.2 RLPSO算法

文献[25]对物种的多样性及雌雄个体之间繁殖后代时的择偶条件等进行了研究，本文以此作为划分粒子群算法的依据，把粒子群中的个体按照生物性别划分为两个群，即雄性子群和雌性子群，不同子群内的个体将执行不同的学习行为。

定义1 (个体分群) 设M表示雌性，F表示雌性，I表示整个种群个体。对于 ∀ i∈I ，则有(gender(i)∈M)∧(gender(i) ∉ F)或 者(gender(i) ∈F)∧(gender(i) ∉M)成立。即个体性别具有唯一性，任意一个个体，或者被划分到雄性子群，或者被划分到雌性子群，不能同时存在于两个不同子群。若整个种群内个体数为N，则雄性子群内个体数Nm=[N/2]，雌性子群内个体数Nf=N-Nm。分群机制如图2所示。

受文献[26]中逆向学习行为启发，生物个体具有逆向学习能力，因此，RLPSO算法内个体除了正向学习之外，以一定概率进行逆向学习。

定义2 (个体学习目标) 对于种群内的任意个体i，其搜索行为受学习目标个体影响。雄性个体的学习目标为雄性子群内最优个体Mb及雌性子群内最优个体Fb，而雌性个体的学习目标为雌性子群内最优个体Fb。

定义3 (个体学习方向) 对于种群内的任意个体i，不管是雄性个体还是雌性个体，都有正向学习行为和逆向学习行为两种模式。设μ(0＜μ＜1)为种群内个体的方向选择概率，rand为产生均匀分布随机数的函数。若rand＞μ，个体选择逆向学习方向；反之，个体选择正向学习方向。在搜索空间内，个体搜索方式及学习方向的选择如图3所示。

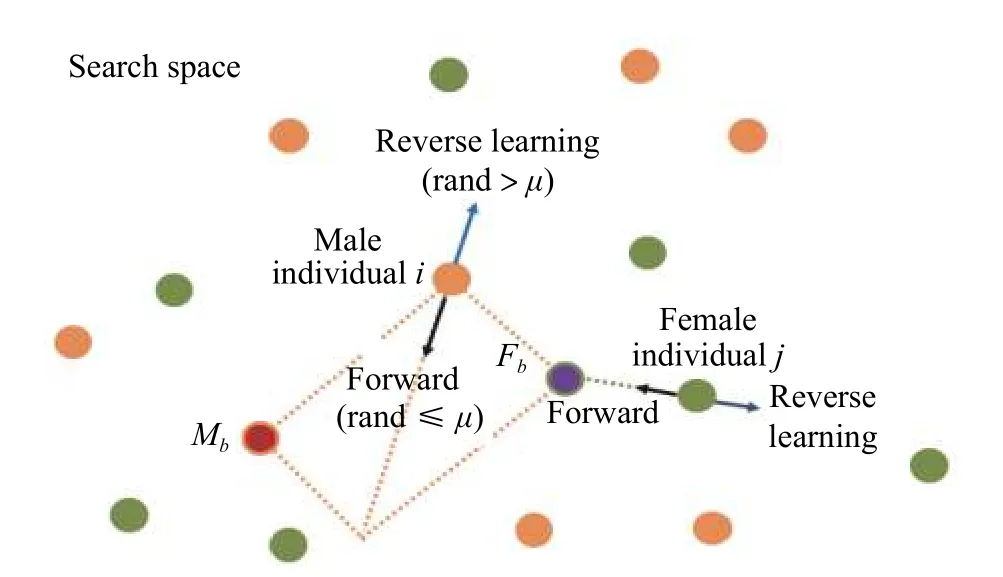
图 3 个体的搜索方式及学习方向Fig. 3 Search mode and learning direction of individual

定义4（雄性个体搜索行为） 由定义2可知，雄性个体选择个体Mb和Fb作为学习目标，由定义3可知，个体有两种学习方向。从而有，当rand＞μ时，个体根据式(7)进行更新位置；当rand≤μ时，个体根据式(8)进行更新位置。

定义5（雌性个体搜索行为） 由定义2可知，雌性个体只选择个体Fb作为学习目标，即学习目标单一性。雌性个体与雄性个体位置更新方式类似，当rand＞μ时，个体根据式(9)进行更新位置；当rand≤μ时，个体根据式(10)进行更新位置。

定义6（繁殖行为） 种群内个体繁殖的目的在于通过产生更优的新生个体替换劣解个体，使得整个种群往更优趋势演化。对于每一轮迭代，任意选择一个雄性个体i，与此同时，个体i将等概率地从雌性子群中选择一个雌性个体j作为繁殖对象，通过繁殖操作，将有一个新的个体xnew产生。繁殖行为如图4所示。

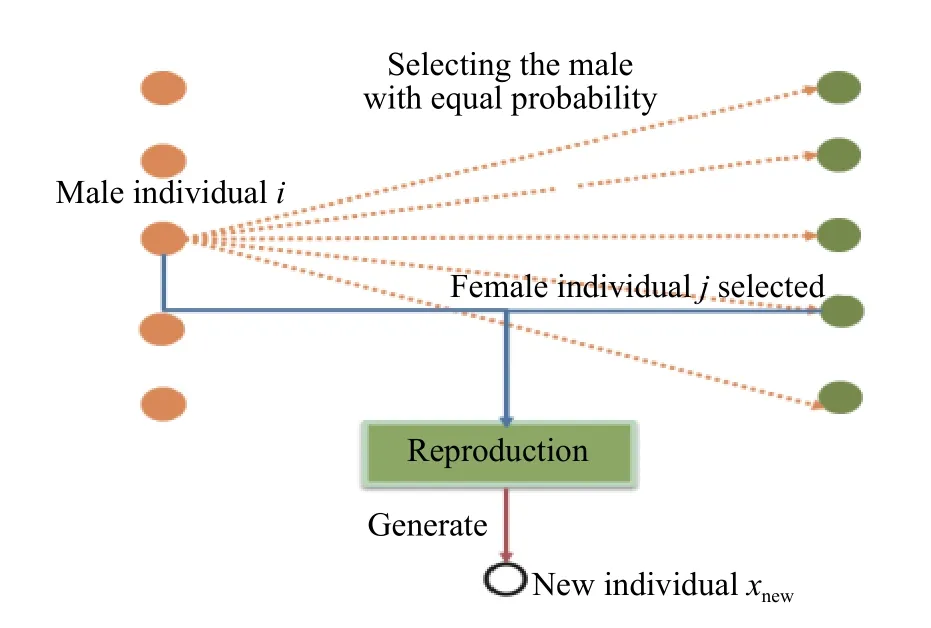
图 4 个体繁殖行为Fig. 4 Reproductive behavior of individual

假设搜索空间内最小边界为Lb，最大边界为Ub，则新生个体在搜索空间中的位置计算公式如下：

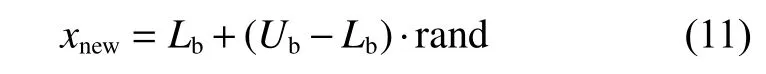
若新生个体的适应值fobejct(xnew)优于种群内最差个体fobejct(xworst)，则淘汰最差个体xworst，并用新生个体xnew替换。反之，若新生个体适应值逊于最差个体，则抛弃新生个体。

由式(11)可知，新生个体可在搜索空间内任一位置产生。对于具有多个极值的问题（即多峰问题），当算法收敛于某个非最优的极值点附近时，借助于新生个体在搜索空间的其他区域产生的方式，可加强算法跳出局部最优的能力。RLPSO算法的伪代码如下：

Input：population size N，iterative number Gn, and parameter μ

Output：The best fitness value and the best task sequence

（1）Initialization；

（2）Generate N individuals randomly；

（3）Set the numbers of females equal to males；

（4）Encoding initial task sequences；

（5）For k=1 to Gn

（6） For i=1 to N

（7） If xiis a male individual

（8） If rand＞μ

（9） Updating position by Eq. (8)；

（10） Else

（11） Updating position by Eq. (9)；

（12） End if

（13） If xiis a female individual

（14） If rand＞μ

（15） Updating position by Eq. (10)；

（16） Else

（17） Updating position by Eq. (11)；

（18） End if

（19） End For

（20） Performing reproductive operation；

（21） Recording the best fitness value and the best position of individual

（22）End For

（23）Decoding the best position；

（24）Return

2.3 收敛性证明

式(7)～式(10)中 Vk(t+1) 和 xk(t+1) 是 多 维 变量，每个维度之间相互独立，故可简化到一维进行证明，并且变量 c1r1可表示成 K1, c2r2可表示成 K2。

引理1 当种群内个体往逆向方向学习时，其位置更新公式满足收敛性。

证明 设

式(8)和式(10)可简化为

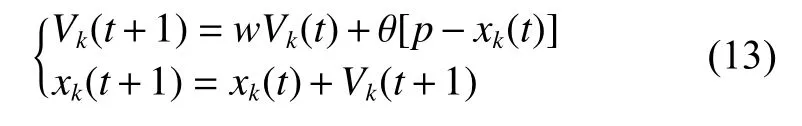
当式(12)中的K2及Mb都等于0时，式(13)即为简化的式(9)。即通过式(13)来同时代表简化的式(7)和式(9)是合理的。

根据动力系统理论，式(13)可重写为

在动力系统y(t+1)中， 若存在一个稳定值 y*，对于 任 意 的t，满 足 y*(t+1)=y*(t) ，则 y*可 根 据 式(12)和式(13)计算得

从动力学理论可知，其收敛性取决于状态矩阵A的特征值。

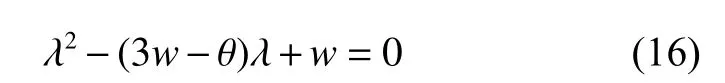
其中，特征值为

动力系统收敛的充分必要条件是 | λ1|＜1 和 | λ2|＜1 ，由 w ＞0 ， c1r1＞0 ， c2r2＞0 ，可 得 | λ1|＜1 且 | λ2|＜1 。从而可证个体进行逆向学习时，其位置移动公式是收敛的。

引理2 当种群内个体往正向方向学习，其位置更新公式满足收敛性。

证明 设

与引理1证明过程相似，其状态矩阵的特征值与 式（17）相似，不同的是， θ 的负值即 θ′，如式（19）所示。

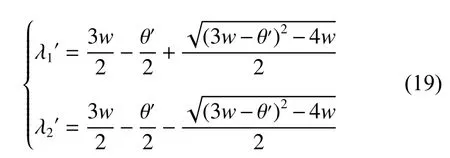
动力系统收敛的充分必要条件是 | λ1′|＜1 和 | λ2′|＜1 ，由 w ＞0 ， c1r1＞0 ， c2r2＞0 ，可 得 | λ1′|＜1 且 | λ2′|＜1 ，即成熟个体位置相斥移动公式是收敛的，从而可证个体进行逆向学习时，其位置移动公式是收敛的。

定理1 RLPSO算法是收敛的。

证明 根据引理1和引理2，可得RLPSO算法内所有个体的移动都将收敛于稳定状态点，即算法满足收敛性。

3 仿真实验

3.1 实验环境及算法参数设置

采用云计算仿真通用平台CloudSim，仿真环境中，计算机的配置环境:操作系统为Windows 10, 内存16 GB，硬盘1TB。资源数量Rn为50, 任务数量Tn分别为100、500、1 000。将RLPSO算法分别与闪电搜索算法(LSA)、粒子群算法(PSO)、遗传算法(GA)、蚁群算法(ACO)4个经典智能优化算法进行比较。5种优化算法的种群规模都为50，迭代次数为200，每个算法分别运行25次。其余参数设置为：(1)PSO算法，惯性权重因子w=1.0，c1和c2取值为2.0[29]；(2)LSA的通道时间设置为10[30]；(3)ACO算法的信息素因子为1.0×10-6、启发函数因子为0.9、信息素挥发因子为0.5、信息素常数为20[31]；(4)GA算法的交叉概率为0.65，变异概率为0.01[32]；(5)为了比较RLPSO与经典PSO的性能，RLPSO的参数w、c1、c2设置与PSO的相同。此外，RLPSO的方向选择概率μ设为0.6。为了客观评价本文算法的性能，采用两个非参数统计技术(Wilcoxon's Test和Friedman Test)对5种算法得到的数据进行性能分析，显著性水平为0.05[33]。

3.2 RLPSO参数择优

经典PSO有3个参数（w、c1、c2），而RLPSO比经典PSO多一个参数(即方向选择概率μ)。RLPSO中w、c1、c2的设置与文献[30]相同，因此，本文只对参数μ进行择优。选用8个基准测试函数作为案例。为了尽量覆盖不同属性的基准测试函数，选择了4个单模函数(f1～f4)和4个多模函数(f5～f8)，即不同属性的测试函数各占一半。这些基准测试函数的详细描述如表1所示。图5示出了8个基准测试函数在三维空间的分布。从图中可以看到，单模函数只有一个最小值，而多模函数有多个极值。

由定义3可知，RLPSO的方向选择概率μ的取值范围为(0,1)，因此，在参数择优过程中，把μ分别设成0.1～0.9(间隔大小为0.1)。对于每个不同的μ，RLPSO在基准测试函数上得到的目标函数值如表2所示。可以看到，当μ=0.6时，RLPSO在f1、f3、f4、f5、f6、f86个函数上表现出最佳性能。对于f2函数，μ=0.7时RLPSO搜索到最优值为3.04×10-2，而μ=0.6时RLPSO得到的最优值为3.47 ×10-2，只比3.04 ×10-2稍微逊色一点。对于f7函数，μ=0.5时结果最好，μ=0.6次之。由于μ=0.6时在大部分函数上都能得到最优结果，表明在该参数值下，RLPSO的搜索性能最好，因此，本文将参数μ设成0.6。

表 1 基准测试函数Table 1 Benchmark functions

图 5 基准测试函数三维空间分布图Fig. 5 Visualization of benchmark functions in three-dimensional space

3.3 任务调度实验结果及分析

图6(a)所示为任务数为100时5种优化算法的总任务完成时间收敛曲线。从图中可以看到，在50次迭代时RLPSO搜索到的值已经优于其他4个优化算法，直到200次迭代RLPSO都表现出了最优的搜索性能，此时搜索到的最优值为12.36 s。在50～200迭代区间，LSA算法仅次于RLPSO。ACO在100次迭代之后处于收敛状态，无法搜索到更优值，搜索曲线为直线状态，此时搜索到的最优值为19.05 s。此时PSO搜索精度略微提高，然而搜索到的最优值逊于ACO。GA算法在50～100次迭代范围内无法搜索到更优值，搜索曲线为直线，100～150次迭代时搜索到一次更优值（29.41 s）之后，其搜索精度再也没有发生变化。可以看出，在任务数为100的条件下，5种算法搜索性能按先后次序排名为：RLPSO、LSA、

ACO、PSO、GA。

表 2 不同的μ值时RLPSO算法的目标函数值Table 2 Objective function values of RLPSO algorothm with different μ

当任务数为500时，5种优化算法的总任务完成时间收敛曲线如图6(b)所示。由于任务数比较大，在50次迭代时，5种算法的搜索曲线已经表现出比较明显的区别，此时算法搜索到的最优值分别为：RLPSO为62.88 s，LSA为82.37 s，PSO为102.33 s，ACO为105.64 s，GA为134.10 s。在50次迭代之后，RLPSO基本处于收敛状态，当迭代次数为200时，其搜索到的最优值为62.50 s，与其他4个优化算法相比，RLPSO呈现出的是快速收敛的能力。LSA算法搜索性能次于RLPSO，其搜索曲线在100次迭代之后接近于收敛状态。PSO和ACO在整个迭代区间的搜索性能都比较接近，直到迭代结束时，PSO搜索到的最优值为88.97 s，而ACO搜索到的最优值为96.18 s。GA算法50～200次搜索到的最优值都逊于其他4个算法，当迭代结束时，其搜索到的最优值为108.93 s。在任务数为500的条件下，5种算法的搜索性能按先后次序排名为: RLPSO、LSA、PSO、ACO、GA。

从图6(c)可以看到，当任务数增加到1 000时，RLPSO的寻优效果最好，搜索到的总任务完成时间为149.34 s。在经过150次迭代之后，LSA、PSO、ACO、GA算法基本处于早熟收敛状态，而RLPSO的寻优曲线还在略微变化，即随着迭代次数的增加，其搜索到更优的值。5个算法中，GA算法的寻优效果最差，在迭代次数为100时，无法再搜索到更优值，并进入收敛状态，此时，GA搜索到总任务完成时间为217.19 s，约为RLPSO搜索到的值的1.5倍。在任务数为1 000时，5种算法的搜索性能按先后次序排名为: RLPSO、LSA、PSO、ACO、GA。

从图6可知，任务数为100、500、1 000时，RLPSO具有最优的寻优效果，特别是任务数为1 000时，RLPSO明显优于其他4个对比算法。

表3所示为3种不同任务数条件下5种算法得到的数据结果。可以看出，RLPSO比其他算法能搜索到更优的结果。图7示出了3种不同任务数时总任务完成时间的柱状图，从图中可以直观看到，在Tn=100时，RLPSO搜索到的总任务完成时间最小，LSA次之，GA总任务完成时间最大。在Tn=500和Tn=1 000时，依然是RLPSO的总任务完成时间最小，GA的总任务完成时间最大。

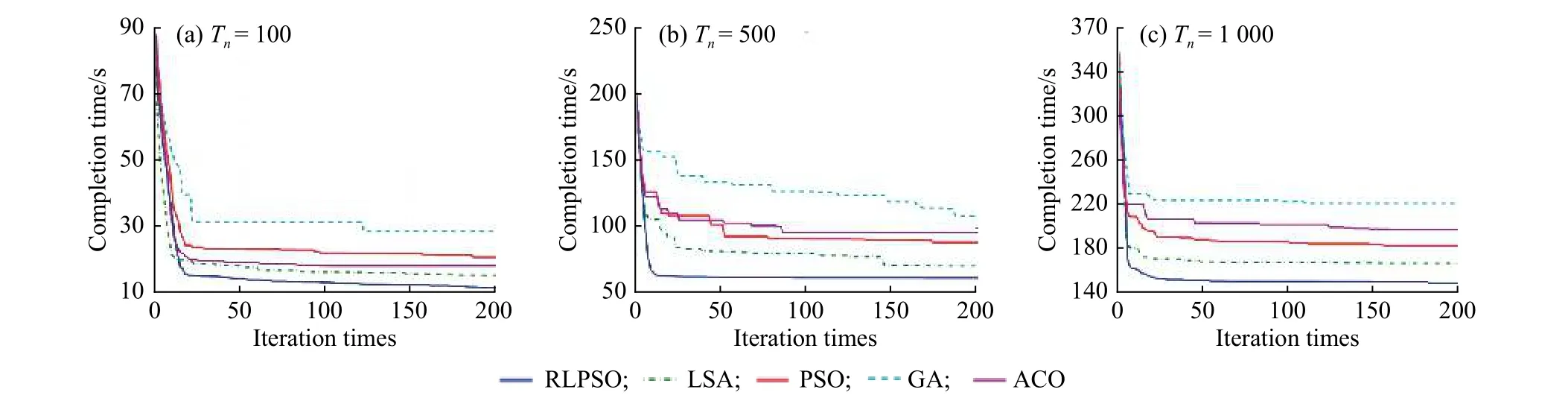
图 6 5种算法在不同任务数下的收敛曲线Fig. 6 Convergence curves of five algorithms under different numbers of tasks

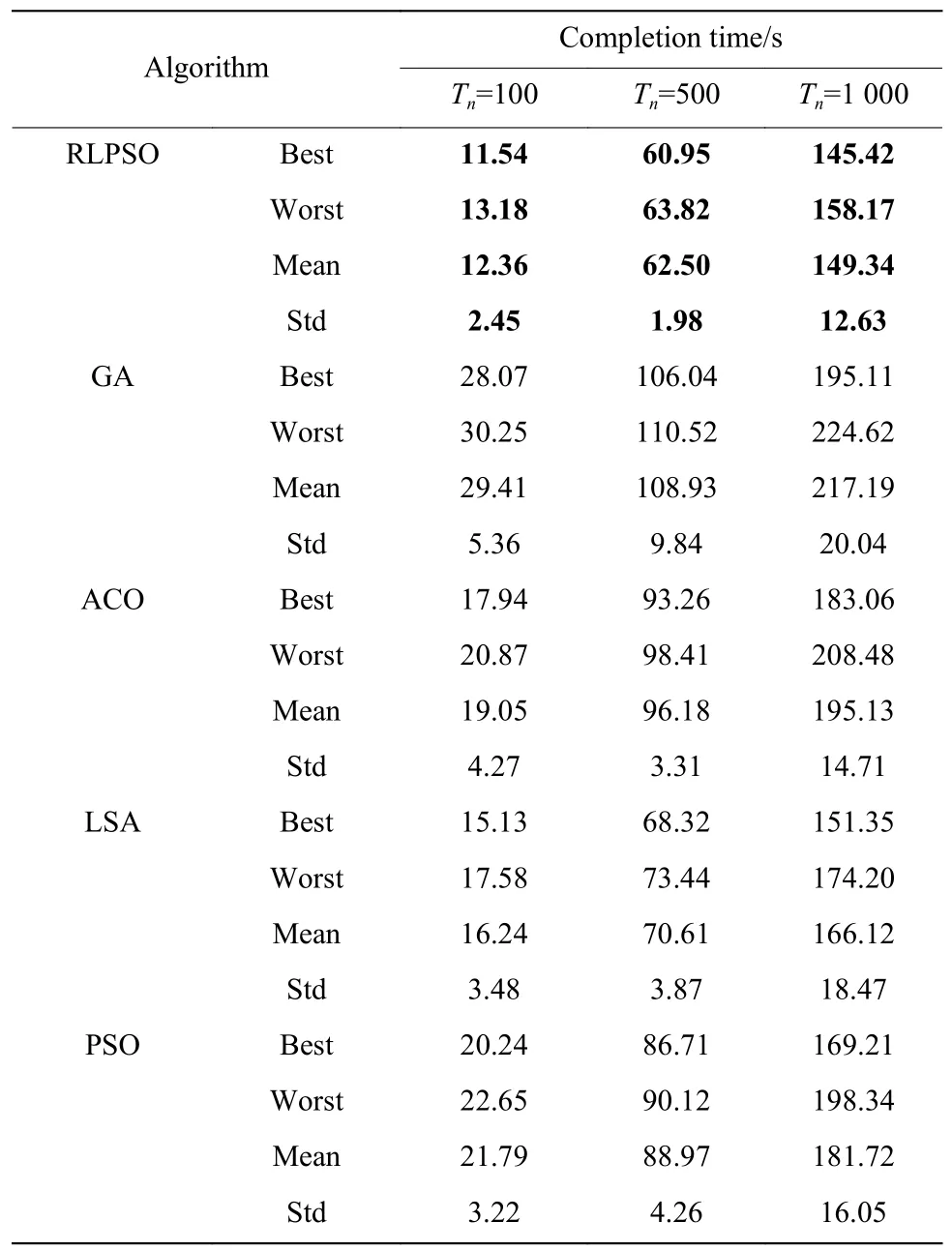
表 3 5种算法3种不同任务数的完成时间Table 3 Completion time of five algorithms under three different numbers of tasks

RLPSO算法与4个对比算法的Wilcoxon's test结果如表4所示。从该表中可以看到p值都小于显著性值（0.05），即RLPSO显著优于4个对比算法。表5给出了5个算法的Friedman test结果，在任务数分别为100、500、1 000时，RLPSO的排名值都是1.00，结果表明本文算法性能最好。

图 7 5种算法3种不同任务数的完成时间Fig. 7 Completion time of five algorithms under three different numbers of tasks

表 4 5种算法Wilcoxon's test的p值Table 4 p-Values of Wilcoxon's test of five algorithms

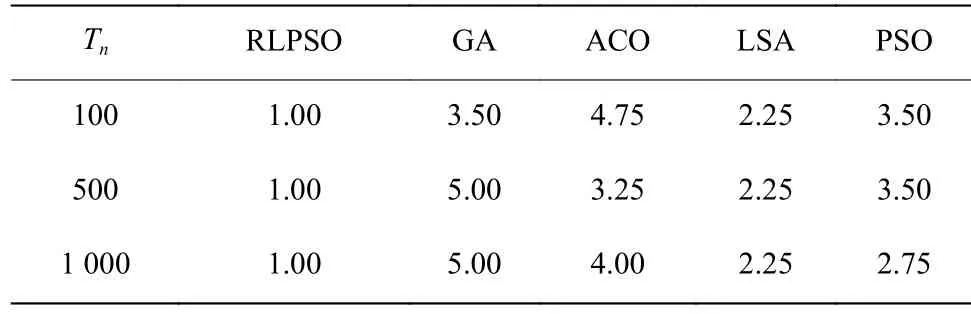
表 5 5种算法的Friedman test排名结果Table 5 Ranking results of Friedman test of five algorithms

从以上实验结果图分析得到，应用RLPSO算法进行任务调度，可以搜索明显更小的总任务完成时间，从而表明RLPSO算法是一种云计算环境下的有效任务调度算法。

4 结束语

本文提出的RLPSO算法通过对粒子进行群划分，引入逆向学习行为，并设计繁殖行为，从而提升整个算法的全局搜索能力和局部搜索能力。在云计算环境下，在任务数分别为100、500、1 000的条件下对RLPSO算法进行了优化性能测试。仿真实验结果表明，与4个传统优化算法(即GA、PSO、ACO、LSA)相比，本文算法具有更优的寻优性能，并且能明显提高对总任务调度时间寻优的效率。目前大部分的优化算法，其灵感主要来源于自然界中的动物生存或植物生长行为。下一步工作将在此改进的粒子群算法的基础上引入粒子竞争行为，从而使得优化算法不再是简单的模拟自然界中存在的现象，而是丰富算法的内部机制，以此形成更具有智能性的优化算法；设计并行计算结构，使得算法在求解大规模问题时能加快计算速度；把改进的算法应用于解决实际问题。