基于微观接触力学的旋塞阀密封面疲劳寿命数值研究
2020-05-07陆俊杰
陆俊杰, 吴 晨, 安 琦
(1. 华东理工大学机械与动力工程学院 上海 200237;2. 安策阀门(太仓)有限公司 江苏太仓 215400)
旋塞阀的密封依靠阀芯与阀座表面的压紧接触,其密封性能主要由阀芯和阀座接触表面的力学性能决定[1-2]。旋塞阀在正常工作过程中,由于所密封的管道内的流体压力始终处于变化状态,导致密封接触面易于发生疲劳破坏,如何对旋塞阀接触面的疲劳寿命进行计算,从而实现对其疲劳寿命的预测,是目前面临的问题之一。
Yuzawa等[3]基于阀座泄漏流量不能超过阀可控的最小流量的准则,提出了一种估计阀寿命的方法。王杭州等[4]研究PEEK阀芯在峰值为70 MPa脉动工作压力下的疲劳寿命,运用传统名义应力法,由PEEK材料的应力-疲劳寿命曲线求得PEEK阀芯在工作过程中的应力-疲劳寿命曲线,结合疲劳损伤累积理论估算出阀芯的疲劳寿命。李玉坤等[5]利用有限元分析软件Workbench建立RMG530减压阀阀体有限元模型,根据现场测得的随机振动载荷对减压阀进行随机振动疲劳分析。高扬[6]基于修正古德曼曲线并结合有限元分析实际应用的阀芯,实现在长时间的疲劳试验前就预判出失效点。王海涛等[7]对隔离阀阀体的高温蠕变疲劳特性进行研究,计算了阀体关键部位的蠕变与疲劳损伤程度,并进一步探索阀体寿命对应力类型和水平的敏感性。Richins等[8]根据USNRC Generic Letter 89-10的测试要求在阀门关闭期间,利用阀芯和阀座之间的超调负载和打开阀门所需的阀杆推力,确定了峰值应力范围以估计由于较高的阀杆推力载荷而导致的疲劳使用系数的增加。陈浩等[9]通过有限元方法对方钻杆旋塞阀本体的疲劳强度进行了分析和试验。金静静等[10]通过宏观分析、化学成分分析、力学性能测试、金相分析及微观形貌分析,对某油田发生的一起钻杆旋塞阀横向断裂事件进行了研究,结果表明旋塞阀的断裂机理为疲劳断裂。冯文荣等[11]采用CFD软件对方钻杆旋塞阀流场进行了三维数值模拟,发现旋钮水平面处的作用力存在3 MPa差异,增加了在该处疲劳损坏的可能性。
综上所述,目前虽然有一些关于阀体密封面疲劳寿命的研究,但这些研究仍然处于较为宏观的层面,鲜有从基于接触面微凸体真实接触的力学行为对旋塞阀接触性能进行的研究,且无法有效地对旋塞阀性能进行定量计算。本文通过采用自相关函数构建真实的旋塞阀三维粗糙接触表面,且基于微凸体接触理论构建旋塞阀预紧及密封面接触的力学模型,在此基础上,也对旋塞阀疲劳失效过程进行了数值模拟。
1 旋塞阀芯与阀座接触力学模型构建
旋塞阀的结构及工作原理如图1所示,旋塞阀分别由螺钉、阀芯、压力盘、垫片、聚四氟乙烯(PTFE)垫片、旋塞阀阀盖与阀体联接螺栓、阀座等组成。密封面接触为阀座金属表面和旋塞金属表面接触,其微观的接触是粗糙表面接触,接触面间的压力主要来自螺栓拧紧力以及管路中的流体压力。

图 1 旋塞阀结构及工作原理图Fig. 1 Scheme of the plug valve structure and working principle
旋塞阀截断关闭时,管道内流体由于外部因素干扰引起压力波动,进而引起旋塞与阀体密封面间接触压力波动,导致了旋塞和阀座密封面微观接触的疲劳积累损伤。随着工作时间增加旋塞与阀座密封面微凸体由于疲劳积累损伤而脱落,接触密封面微凸体脱落个数增加最终导致旋塞与阀座密封面发生泄漏失效。
1.1 旋塞阀阀芯与阀座接触力分析
在安装过程中,旋塞阀螺钉拧紧 N 圈后实现阀芯与阀座的接触面压紧,此时螺钉、压力盘、垫片等发生弹性变形。螺钉拧紧 N 圈后,将有 n 对内外螺纹相互啮合,根据文献[12],建立紧定螺钉拧紧圈数与压紧力变形协调关系,通过数值计算,可以求出螺钉拧紧 N 圈后对旋塞所产生的压紧力 FN。
工作过程中旋塞阀阀芯受力示意图如图2所示。旋塞处于闭合状态时,进口端压力为 pin,出口端压力为 pout,旋塞左、右侧密封面接触应力分别为σl、σr,这时旋塞和阀座之间的接触压力使其产生密封效果,管内流体压力作用在旋塞上的合力(进出口压 力积分得) FP为:

式中:p=pin-pout;r为xoy平面旋塞曲率半径;α为旋塞相位角(如图3(a)所示);R2、R3为管道流体压力在z方向上的作用界曲率半径。
旋塞阀密封面接触模型示意图如图3所示,当管内通有流体时,旋塞与阀座接触面上的压力呈不均匀分布状态,由于受力的不平衡,导致阀座沿圆周方向上的弹性接触变形不均匀,表面微观接触面积远小于宏观尺度上接触面积,阀芯宏观尺度上虽然几乎不发生改变,但密封接触面的弹性压缩量的不均匀将会导致阀芯受压发生偏移。将旋塞接触面沿轴向展开,并进行网格化,如图2所示,每个网格上的接触压力都不相等。
每个网格的弹性压缩量 Δsi,j可以表达为:
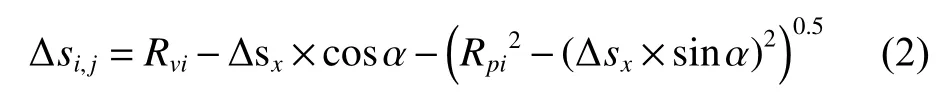
式中: Δsx为阀芯位移; Rvi为接触微单元上阀芯平均半径; Rpi为接触微单元上阀座内圈平均半径, Rpi=Rvitan2°×Δs,Δs为阀芯在 z 方向上的位移。
微单元接触面积 Ai,j为
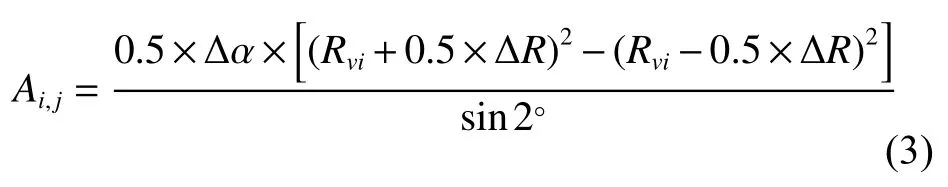
式中:ΔR为旋塞密封面微单元曲率半径的增量。
微单元接触高度 Δsi的数值计算基于赫兹接触力学,每个接触单元的接触力 Fi,j,水平方向上的合力p为

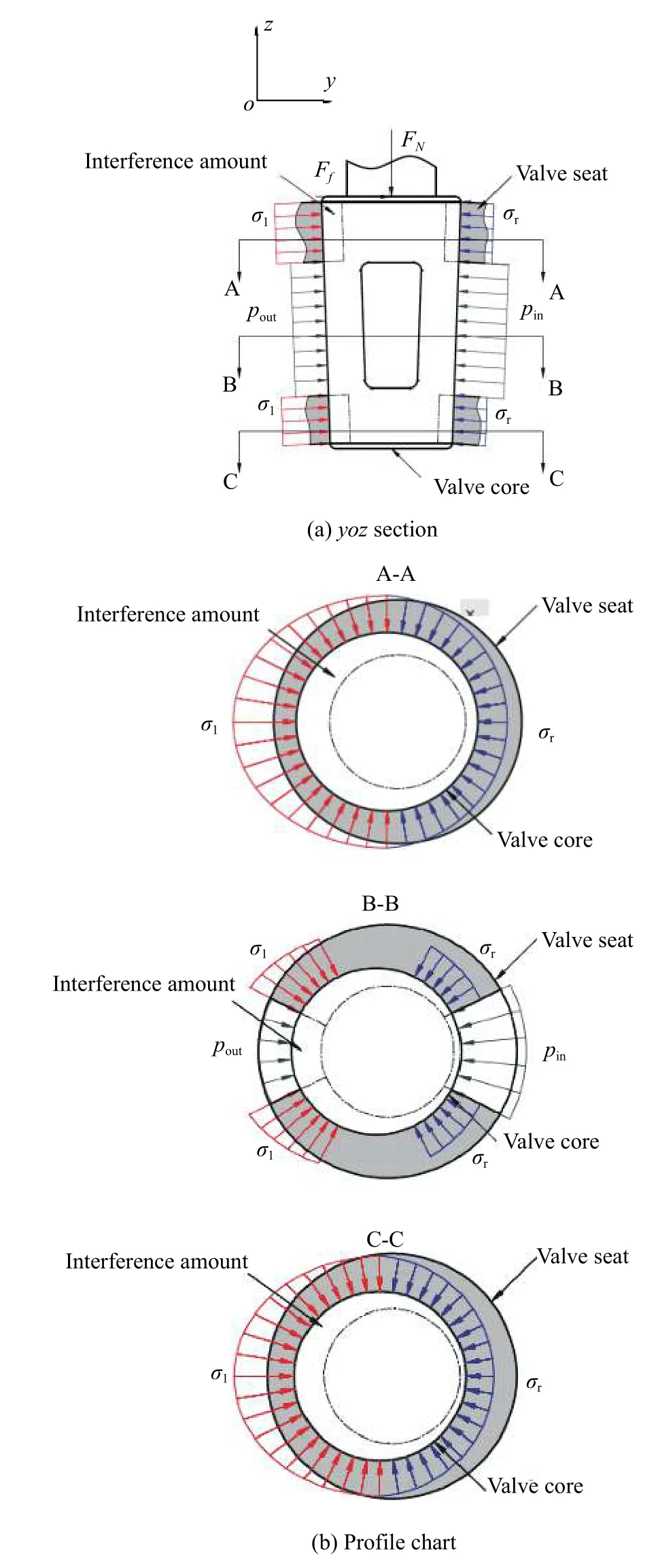
图 2 工作过程中旋塞阀阀芯受力示意图Fig. 2 Force diagram of the plug valve cock during working
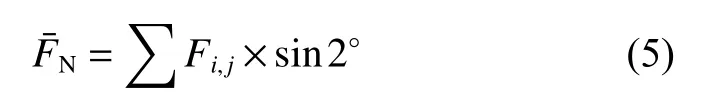
1.2 密封面接触力学模型构建
旋塞与阀座密封面实际的接触表面是粗糙的表面,在计算每个接触单元的接触力时,应考虑微观接触的受力变形。为此,本文采用自相关函数[13-15]构建旋塞阀座套筒的接触表面:

其中, σ 为表面均方根粗糙度; x 为密封圈接触面圆周方向坐标,y为密封圈接触面轴向坐标,分别为 x 、y方向任意两点之间的距离;分别为x、y方向上的相关长度。
旋塞阀密封面微单元接触模型如图4所示,数值计算微单元的三维随机粗糙表面(粗糙度Ra=0.5),采用接触密性数值计算抛光后加工的不锈钢材料三维粗糙表面,并赋予随机表面相应的力学性能参数。旋塞阀螺钉拧紧 N 圈后,管内流体压力波动值在时,旋塞与阀座两表面第(i, j)对密封微单元叠放接触(如图4(c)所示),该微单元接触应力云图如图4(d)所示。
微观上,两密封表面的接触实际上是两个表面上微凸体之间的接触。对于单个微凸体间的接触,可以将接触面近似看作球面接触,两微凸体的微观接触状态如图5所示。其中:分别为两微凸体接触面曲率半径;为单对微凸体的接触高度;为单对微凸体接触力平衡的外载荷;为单对微凸体的接触面积。
本文假设接触过程中微凸体只发生弹性变形,采用赫兹接触理论来研究接触力、接触变形与外载荷之间关系。根据赫兹接触理论,两球形微凸体发生点接触,接触力最大接触应力与微凸体的 接触高度关系式为[16-17]:


结合旋塞阀密封面粗糙度的影响,利用上述模型可计算出在不同过盈量下旋塞阀阀芯与阀座在不同过盈量下密封面接触力分布。根据文献[18]中油气管道雨流计数的波动压力采集数据进行结果分析,得到旋塞阀管道流体压力波动分布规律为随机分布。按此分布规律使用Matlab内置函数randsample数值模拟管道内压力随时间波动,结果如图6所示,可进一步得到旋塞阀管内流体压力随时间波动值,管内流体压力极限pmax、流体压力平均值 pmean、流体压力幅值 pa和管内流体压力幅值比 rp。

图 3 旋塞阀密封面接触模型示意图Fig. 3 Diagram of plug valve sealing surface contact model
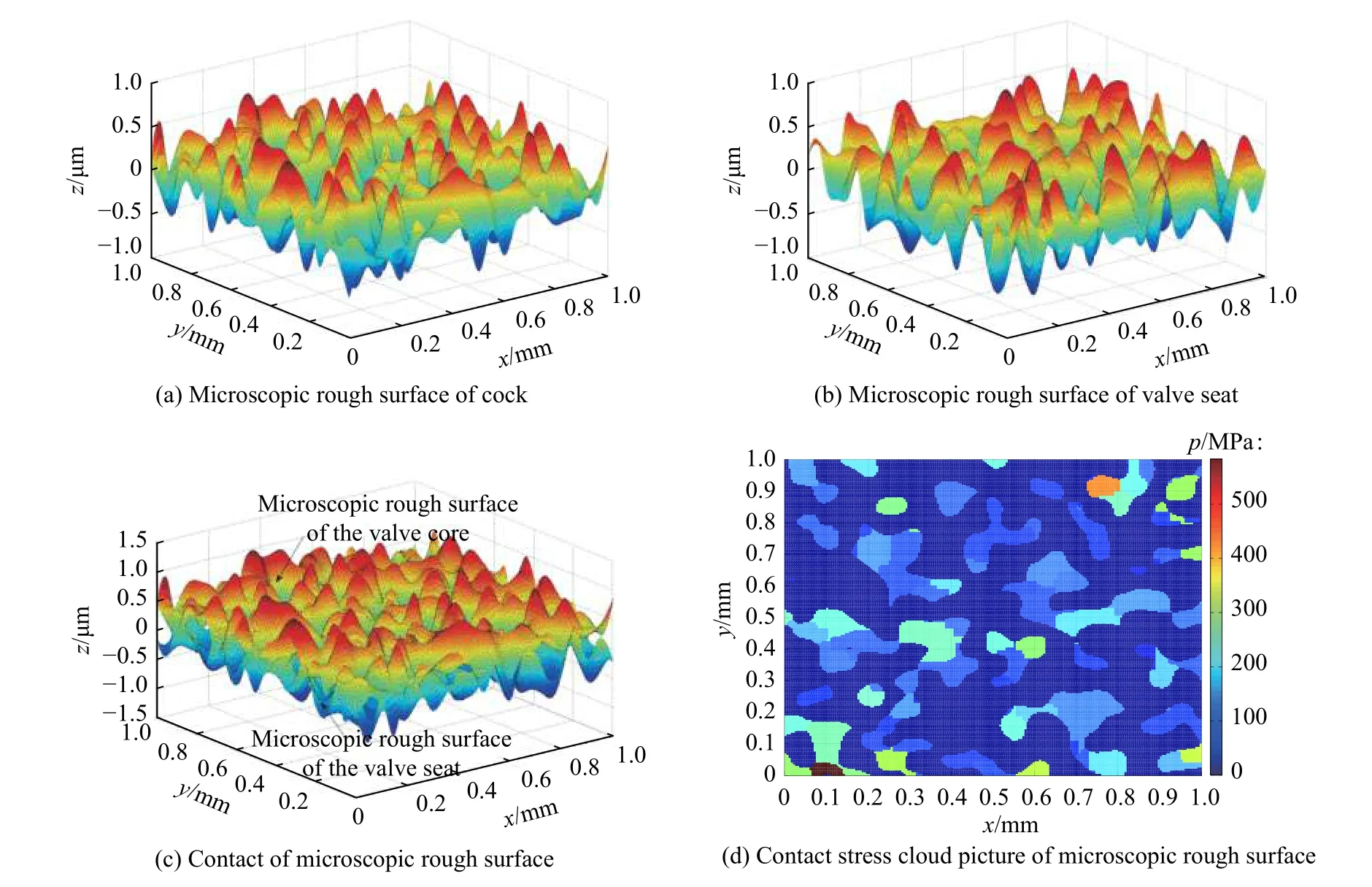
图 4 旋塞阀密封面微单元接触模型Fig. 4 Plug valve sealing surface micro unit contact model
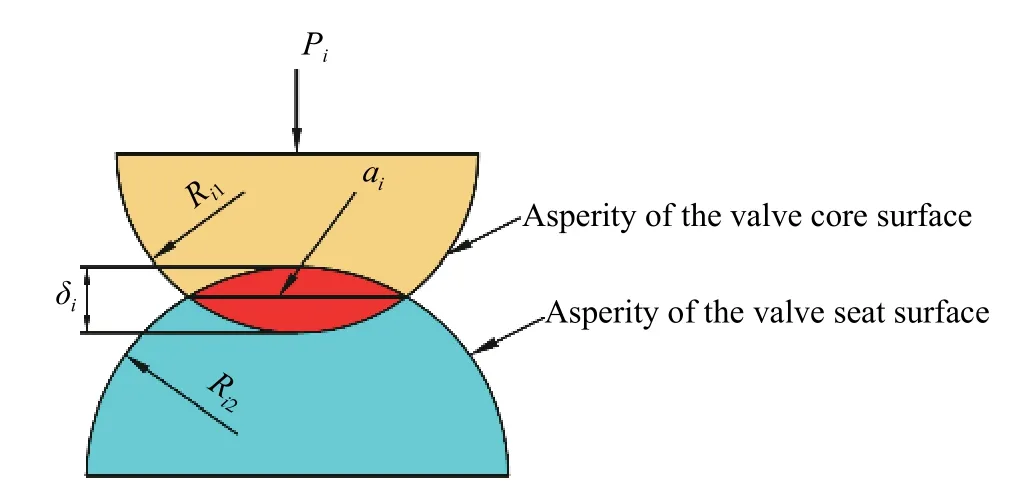
图 5 单个微凸体接触简化模型Fig. 5 Simplified model of a single pair of asperities contact
管道内流体压力随机变化引起旋塞阀密封面接触应力变化,将导致接触面的疲劳破坏。根据文献[19]提出的线性疲劳累积损伤计算方法,将各应力相对应的累积循环次数与材料发生疲劳破坏时的极限循环次数商的总和定义为材料的总寿命损伤,理论上该值为1,即:
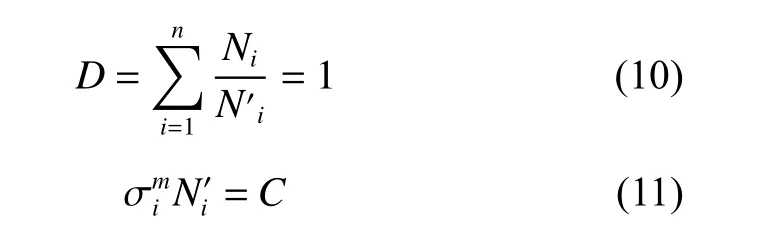
其中:D为总寿命损伤; σi为密封圈接触表面的应力幅;Ni为各应力相对应的累积循环次数; Ni′为与各应力相对应材料发生疲劳破坏时的极限循环次数。
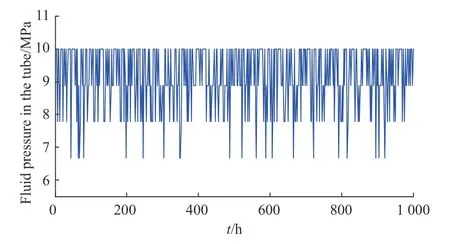
图 6 管道内流体压力波动随时间变化曲线Fig. 6 Curve of fluid pressure fluctuation over time in a pipe
考虑工程应用数据难易度,本文选取丁氏的估算公式[20]:
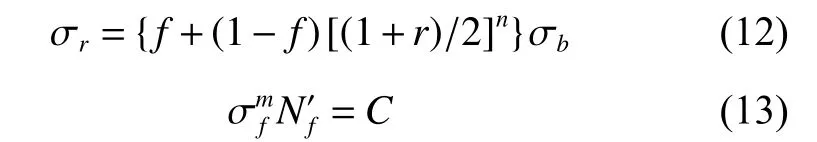
其中:σr为应力比为 r 时交变应力中最大应力的极限值; f 为材料的疲劳比( f=σ-1/σb,σ-1为对称循环下材料的疲劳极限,σb为材料静抗拉强度极限);n 为材料常数,与 f有关, n=1/(cf)( c 为待定系数);σf为应力比为r 时交变应力中应力幅的极限值;m是疲劳曲线指数; N′f为达到疲劳极限的循环次数。
微凸体发生疲劳失效后密封面微观接触示意图如图7所示。计算微凸体发生疲劳失效后密封面微观接触微单元的弹性压缩量 Δsi,j,得到该状态下旋塞阀接触单元的接触力 Fi,j。根据文献[21]中的密封面泄漏识别算法,判定密封面是否泄漏,如果密封面出口通道出现标记值-1,即旋塞阀密封面发生泄露,则判定旋塞阀与阀座密封失效,如图7(b)所示。
1.3 旋塞阀密封面疲劳寿命数值计算流程
旋塞阀密封性能数值计算流程图如图8所示,具体步骤如下:
(1)给定旋塞阀预紧圈数 N ,密封面粗糙度 Ra,旋塞阀工作时间 Ti=Ti-1+ΔT ,进、出口端流体波动压力值为 pin、pout;
(2)计算管内流体压力作用在旋塞上的合力 FP,旋塞所产生的压紧力 FN,微凸体发生点接触最大接触应力 σimax;
(3)判断密封面每一个微凸体是否发生疲劳失效,如果微凸体发生失效,则失效微凸体不再参与密封面接触力计算;否则,密封面保持不变;
(4)根据文献[21]中的密封面泄漏识别算法,判定密封面是否泄漏,如果密封面发生泄露,那么旋塞阀密封面失效;否则,重复计算步骤(1)至步骤(4)。
(5)输出旋塞阀密封面关闭状态的疲劳寿命t。
2 算例研究
基于上述计算模型,以金属接触密封圆锥形旋塞阀为对象,研究了旋塞阀密封面疲劳泄漏前预期寿命 t 随着紧定螺栓预紧圈数 N 、旋塞压紧力 FN、密封面粗糙度 Ra以及管内入口处流体波动压力 pin等参数的变化规律。以安策阀门公司F-2 ISOSTANDARD(1'')旋塞阀外形尺寸为数值计算研究对象,具体参数如表1所示。

图 7 微凸体发生疲劳失效后密封面微观接触示意图Fig. 7 Schematic diagram of micro-contact on sealing surface after fatigue failure of asperities
2.1 旋塞阀疲劳寿命分析
根据文献[18]中油气管道雨流计数的波动压力集数据结果,分析得到管道流体压力波动分布规律,同时探讨了管道入口压力随时间波动的变化情况,得到流体压力平均值为 2.5MPa ,流体压力幅为2.5MPa,流体压力比为 0 。旋塞阀密封机构基体疲劳失效寿命即为密封面最大接触应力引起的疲劳失效寿命,根据文献[22]的实验数据,得到304不锈钢疲劳寿命实验常数为 8.8496,疲劳极限(=107时)为 187.51MPa 。

图 8 旋塞阀密封性能计算流程图Fig. 8 Calculation flow chart of sealing performance of plug valve
旋塞阀密封面疲劳泄漏前预期疲劳寿命随旋塞压紧螺钉拧紧圈数变化规律如图9所示。在相同粗糙度下,旋塞阀密封面疲劳泄漏前的预期疲劳寿命随着旋塞阀紧定螺钉拧紧圈数的减小而增加,这是由于拧紧圈数减少,其接触面的接触应力也会减少。在相同螺钉拧紧圈数的情况下,接触面的粗糙度越大,预期疲劳寿命也会越大。研究发现当旋塞阀密封面粗糙度为 1.1 ,紧定螺钉拧紧圈数小于0.11时,旋塞阀密封面泄漏通道已经形成,此时该密封面预期疲劳寿命最大值为 6.382×106h ,将不会出现密封面无限疲劳寿命区。

表 1 F-2 ISO-STANDARD(1'')旋塞阀的基本参数Table 1 Parameters of plug valve F-2 ISO-STANDARD (1'')
为了对图9的计算结果进行验证,不考虑微观粗糙表面接触泄漏,仅考虑最大接触应力旋塞与阀座疲劳失效前的旋塞阀疲劳寿命与螺钉拧紧圈数之间的关系(如图10所示)。结果发现,本文建立旋塞阀密封面疲劳泄漏前预期寿命与考虑最大接触应力旋塞与阀座疲劳失效前的旋塞阀工作寿命对应的紧定螺钉拧紧圈数的变化规律基本一致。数值上,在相同旋塞阀密封面粗糙度,相同螺钉拧紧圈数下,根据本文建立密封面疲劳泄漏模型数值计算的旋塞阀密封面疲劳寿命较高,表明本文建立的旋塞阀密封面疲劳寿命算法是可靠的。
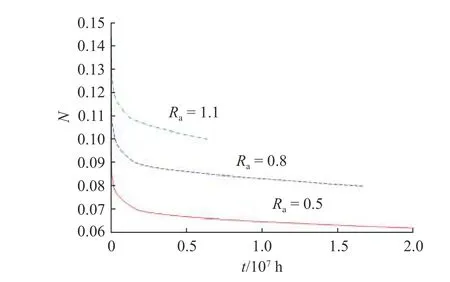
图 9 旋塞阀密封面泄漏前疲劳寿命与螺钉拧紧圈数之间的关系Fig. 9 Relationship between fatigue life and numbers of screw tightening cycles before sealing surface leakage of plug valve

图 10 旋塞与阀座疲劳失效前的旋塞阀疲劳寿命与螺钉拧紧圈数之间的关系Fig. 10 Relationship between the fatigue life of plug valve and the numbers of screw tightening cycles before the fatigue failure of cock and valve seat
旋塞阀密封面疲劳泄漏前预期疲劳寿命随旋塞压紧力变化规律如图11所示。在相同粗糙度下,随着旋塞压紧力减小,旋塞阀密封面疲劳泄漏前的预期疲劳寿命将会增加。在相同旋塞压紧力下,接触面的粗糙度越大,预期疲劳寿命越小。这是由于相同的旋塞压紧力下,粗糙度高的接触微观表面实际接触面积较小。研究发现当旋塞阀密封面粗糙度为1.1、旋塞压紧力小于 3 .25×104N 时,旋塞阀密封面泄漏通道已经形成,导致旋塞压紧力继续减小,密封面预期疲劳寿命都为0,将不会出现密封面无限疲劳寿命区。

图 11 旋塞阀密封面泄漏前疲劳寿命与对应的旋塞压紧力之间的关系Fig. 11 Relationship between the fatigue life of the sealing surface of the plug valve before leakage and the corresponding pressure of the cock
基于接触表面微观疲劳泄漏模型研究管内波动流体压力幅值对旋塞阀密封面疲劳寿命影响,结果如图12所示。当管内流体平均压力值为 5 MPa 、螺钉拧紧圈数为 0 .05 时,旋塞阀密封面疲劳寿命随管内流体压力幅值的增加而减小,增速随管内流体压力幅值的增加而增加。这是由于管内平均压力不变时,管内波动流体压力幅值增加,其密封面微凸体波动接触应力幅值增加且微凸体接触应力比减小所致。

图 12 旋塞阀密封面疲劳寿命与管内波动流体压力幅值之间的关系Fig. 12 Relationship between the fatigue life of the sealing surface of the plug valve and the amplitude of fluctuation fluid pressure in the pipe
基于接触表面微观疲劳泄漏模型研究管内波动流体压力幅值比对旋塞阀密封面疲劳寿命的影响,结果如图13所示。当管内流体压力极限值为 1 0MPa 、螺钉拧紧圈数为 0 .05 时,旋塞阀密封面疲劳寿命随管内波动流体压力幅值比增加而增加,增速随管内流体压力幅值比增加而放缓。这是由于管内流体压力幅值比增加,管内流体压力极限值不变时,其密封面微凸体接触应力比增加且接触应力幅值减小所致。

图 13 旋塞阀密封面疲劳寿命与管内波动流体压力幅值比之间的关系Fig. 13 Relationship between the fatigue life of the sealing surface of the plug valve and the amplitude ratio of fluctuation fluid pressure in the pipe
基于接触表面微观疲劳泄漏模型进一步研究管内波动流体平均压力对旋塞阀密封面疲劳寿命影响,结果如图14所示。当管内流体压力幅值为1 MPa、螺钉拧紧圈数为0.05时,旋塞阀密封面疲劳寿命随管内波动流体平均压力的增加先增加且增速放缓,达到极值后减小,且减速变大。这是由于管内流体压力波动幅值不变时,平均压力增加,其密封面微凸体接触平均应力增加且接触应力波动幅值减小,管内流体在相对低压处接触面微凸体疲劳寿命受接触应力幅值减小的影响较大,在相对高压处受平均接触应力增加的影响较大所致。

图 14 旋塞阀密封面疲劳寿命与管内波动流体平均压力之间的关系Fig. 14 Relationship between the sealing surface fatigue life of plug valve and the mean pressure of fluctration fluid in the pipe
3 结 论
(1)以旋塞阀密封性能为研究对象,对旋塞阀的结构进行分析,考虑流体压力波动作用,建立了旋塞阀紧定螺钉和旋塞阀阀芯的变形协调关系模型;同时采用自相关函数构建微观粗糙表面,对旋塞阀密封面接触进行受力分析,建立旋塞阀密封面泄漏识别算法;通过数值计算方法对旋塞阀密封面微凸体线性疲劳损伤进行求解,并对旋塞阀阀芯与阀座接触面密封疲劳寿命进行计算。
(2)随着螺钉拧紧圈数、旋塞压紧力增加,旋塞阀密封面疲劳泄漏前预期寿命将减小;在相同螺钉拧紧圈数下,旋塞阀密封面疲劳泄漏前预期寿命随粗糙度增加而增加;在相同旋塞压紧力下,旋塞阀密封面疲劳泄漏前预期疲劳寿命随粗糙度增加而减小。应用本文建立的基于微观接触微凸体线性疲劳积累损伤引起密封面泄漏模型的旋塞阀密封面疲劳寿命数值计算结果,由于考虑密封面微观泄漏失效,因而不会出现无限寿命区。
(3)若管内流体平均压力值相等,则旋塞阀密封面疲劳寿命随管内流体压力幅值增加而减小;若管内流体压力极限值保持不变,则旋塞阀密封疲劳寿命随管内流体压力幅值比增大而增大;若管内流体压力幅值保持不变,则旋塞阀密封疲劳寿命随管内流体平均压力的增加先增加再减小。
