中国股市极值收益率的长记忆性研究

苑 莹，张同辉，庄新田

(东北大学工商管理学院，沈阳 110167)

0 引言

20世纪90年代以来，国际金融市场危机四伏，全球性金融危机频繁发生，尤其是2008年由美国次贷危机所引发的全球性金融危机，其规模与危害更是史无前例：各国主要金融市场总体出现持续动荡，由此衍生出的极端波动性、市场突发性、市场复杂性等特征不断地侵蚀着金融安全，也给实体经济带来了严重损害，这无疑对金融风险管理提出了巨大挑战。

在金融市场中，金融资产价格的极端波动(暴涨暴跌)常常会引起投资者、金融机构以及市场监管部门的极大关注。对于金融极端事件，人们往往会产生如下疑问：金融市场价格的极端波动行为有无规律可循？金融资产价格极值收益率服从何种分布？能否借助对金融市场已有极端波动行为的研究成果实现对金融市场未来极端波动事件的有效防范和预警？上述问题无疑是当前国际金融市场亟待解决的问题。作为金融市场最重要的特征之一，正常情况下，金融市场的价格波动应该保持在一个合理的范围内，波动太小说明市场缺乏流动性，波动太大则易导致金融危机，因此，对于风险，尤其是这类极端风险的防范仍不可小觑。

大量研究金融市场统计规律的相关文献已表明金融市场的资产收益率和收益波动率均具有显著的长记忆性，如股票市场、外汇市场、期货市场、原油市场、衍生品市场等。长记忆性意味着所观测的样本数据具有高度持久性，它描述的是序列的高阶相关结构。换句话说，资产收益率的长记忆性意味着资产收益随着时间持续相关并且在一定程度上可测。因此，深入研究资产收益的长记忆性特征，对于验证市场结构和有效市场假说、管理控制金融风险和投资组合，具有重要的理论意义和实践作用。

1 文献综述

许多国内外学者对不同市场的长记忆性及可预测性进行了深入的研究并得到了一些有意义的理论成果[1-2]。如在股票市场方面，Greene &Fielitz最早运用R/S分析(重标极差分析)方法对美国股票市场进行深入研究，结果发现其确实存在一定的长记忆性特征[3]。Norouzzadeh等运用不同的统计分析方法对伊朗股票市场的Tehran股指收益序列进行实证研究，发现该序列具有明显的长记忆性特征，并进一步发现广义Hurst指数H(1)与H(2)的值与资本市场的发展状态相关[4]。Mariani等选取了美国市场中的25支股票，结合R/S分析方法、DFA(消除趋势波动分析)方法尝试对高频数据进行检验分析，结果一样证实了收益率序列的长记忆性特征[5]。Kasman主要针对中欧、东欧等国家展开实证研究，采用FIGARCH、GPH、ARFIMA等多种模型，再一次验证了长记忆性特征[6]。Bisaglia[7]及Melo Mendes[8]与以上研究内容有所不同，两位学者重点探讨结构突变是否与长记忆性存在某些关联，结果发现，结构突变并不能导致长记忆性，由此说明长记忆性一直存在于市场本体内，这对金融风险管理者具有重要的实践指导意义。此外，Barkoulas等对希腊股市[9]、Sensoy&Tabak对欧盟股票市场[10]、Caporale对乌克兰股票市场[11]、Lonnbark对世界7个主要国家的股票市场[12]、Li等对世界30个主要国家的股票市场[13]的长记忆性分别进行了确认，上述研究证实了股票市场具有长记忆性这一典型事实。在外汇市场方面，Bhar运用修正的R/S分析方法，检验了日元对美元汇率是否具有一定的长记忆性特征，实证结论是否定的，即并不存在长记忆性特征[14]。Alptekin运用KPSS、修正R/S分析等多种统计方法实证检验了美元对新土耳其汇率的长记忆性特征，结果发现其时间序列具有明显的长记忆性特征[15]。Oh等运用DFA(消除趋势波动分析)方法，尝试探究股票市场及外汇汇率的高频波动率和收益率是否具备此特征，结果表明高频收益率序列未能呈现出显著的长记忆性，而高频波动率序列具有明显的长记忆性特征[16]。Kang等运用时变的Hurst指数方法对亚太地区7种外汇汇率的长记忆性进行实证检验，确认了外汇市场的长记忆性特征[17]。此外，一些学者还对期货市场、期权市场的长记忆性进行了实证检验，如Souzaa等运用R/S分析方法确认了美国利率期货的长记忆性特征[18]、Coakley等确认了17种商品和金融资产的长记忆性[19]。Chkili等运用DCC-FIAPARCH模型实证研究了原油市场及其美国股市的长记忆性特征，确认了原油市场及股票市场中长记忆性特征及非对称行为特征的存在[20]。国内学者近几年也围绕金融市场长记忆性这一课题进行了深入探索，取得了一系列有意义的理论成果。如王鹏和魏宇[21]、杨科[22]等分别对中国沪深300股指期货及中国股市波动率的长记忆性与可预测性进行了有益的探讨。曹广喜利用长记忆动态VAR模型实证分析了中国汇市与股市的长记忆性特征，并进一步研究了汇市与股市间的动态冲击影响关系[23]。苑莹和庄新田等从价-量交叉相关性视角，对中国股市日内效应、长记忆性及多重分形性等特征进行了实证检验，深入探讨了市场价格波动行为[24]。谭政勋等利用精准局部似然函数法对上海股票市场进行实证研究，确认了股票市场的长记忆性及趋势预测性[25]。田存志等对金融市场长记忆性进行了研究综述，对长记忆性的相关理论基础、研究方法、经验证据等进行了较为全面的梳理[26]。

综上所述，显而易见的是，现有学者对于股票市场可预测性和长记忆性的相关研究，大多局限于整体时间段内的交易量序列、价格波动序列或收益率序列，而未充分考虑巨幅波动中该特征是否成立，也鲜有学者将金融市场的极值收益率序列作为研究对象进行深入研究。实际上，资产价格的极端波动意味着金融市场的震荡以及资产价值的剧变，外部宏观环境的巨幅波动可能会对长记忆性特征产生一定的冲击，极值收益率的研究对估计市场风险和规避风险有着重要的指导意义。因此，对金融市场极值收益率的波动行为特征机理的认识是理解市场波动性的关键。基于此，在2008年金融危机背景下，从研究金融市场极端波动行为的视角出发，本文对中国股市极值收益率的长记忆性进行了探讨和研究，本文的主要贡献在于：采用极值收益率序列作为实证研究对象，运用自相关函数及互相关函数、R/S(重标极差)方法、DFA(消除趋势波动分析)方法等多种计量方法对上海股票市场极值收益率的长记忆性进行了实证研究，研究结果表明极值收益率序列和极值波动率序列的长记忆性特征都较为显著，其中，极值收益率序列和极值波动率序列的特征要更为突出，而收益率序列本身的特征相对较弱。此外，本文进一步分析了极大值及其相应波动率序列之间、极小值及其相应波动率序列之间以及极大值与极小值之间的互相关关系。

2 数据选取与描述

本文实证数据来源于上海证券交易所(SHSE)，所选取的数据为上海股票指数(SHSI)每日收盘价。现有学者对长记忆性的研究一般基于常态经济背景，而较少对非常态经济下极值收益率序列的动态变化特征进行考察，而2008年金融危机恰好为我们的分析提供了研究契机。为了更好地扑捉2008年金融危机时期频繁发生的极端波动事件，因此本文所选取的上证指数样本时间区间从上证指数开盘的1990年12月20日到2010年12月30日(2008年金融危机结束一段时间之后)，将危机中巨幅波动数据纳入极值收益率序列，对该特殊时间段内的动态变化特征进行深入统计剖析。在整个样本区间内我们关注对数收益率和日波动率(收益率的绝对值)。图1列示了在样本整体时间段内，股票价格指数的变动特征。表1列示了波动率序列和收益率序列的具体统计量数值。由表1数据可初步分析：1)两个不同序列的偏度统计数值均大于0，证明序列分布为右偏，说明收益率出现负值的可能性要小于波动率序列和收益率序列为正值的可能性。2)两个序列的峰度统计量均大于3，由此可以初步分析出，这两个序列具备“尖峰态”特征，不服从正态分布，且波动率序列的峰度大于收益率序列的峰度，说明波动率序列具有更尖的峰。由此可以看出，收益率序列与波动率序列均具有“尖峰厚尾”的分布特征。

表1 收益率序列和波动率序列的基本统计量

图1 上证指数随时间变化趋势图Fig.1 Evolution of the Shanghai stock price index

3 实证研究

3.1 极值收益率序列的统计特征

图2以2008年金融危机期间为例，列示了上证指数收益率序列连续100天的趋势图。为了与文献[27]的结论进行对比，这里也以R=4为例，研究样本时间段内的极值收益率序列(实际上，当R选取不同数值时，结论仍然是稳健的，由于篇幅所限，本文未一一列示)。图2同时列示了当长度R=4时，由原始对数收益率序列中选出的极大值和极小值序列mR(t)。从图中可以清楚地看出，极大值序列和极小值序列的个数是原始序列个数的1/4。接下来的研究中我们将重点关注极值序列(极大值序列和极小值序列)，并进一步研究极值序列的长记忆性。

图2 金融危机时期R(时间间隔)=4时 上证指数极大值(星形)和极小值(圆圈)收益率序列Fig.2 The maxima (stars) and minima (circles) time series of the SHSI daily returns for the interval R=4 in the period of financial crisis

图3给出了当R=4时全样本极大值和极小值收益率序列的趋势图。图3中的两条水平线分别代表着极大值收益率和极小值收益率的均值。在图3中，可以看出在均值上下(小的和大的)极大值和极小值收益率序列呈现出聚类特征，这些聚类特征意味着长记忆性特征的存在，即大的极大值(极小值)后面趋向于跟着大的极大值(极小值)，小的极大值(极小值)后面趋向于跟着小的极大值(极小值)。收益(极大值)的聚类特征意味着在R的时间间隔内大的收益往往跟着下个时间间隔内大的波动。对于损失(极小值)，反之亦然。类似地，图4给出了当R=4时整个样本时间上的极大值和极小值的波动率序列。图4中的两条水平线分别代表着极大值波动率和极小值波动率的均值。

图3 R=4时收益率序列的 极大(Maxima)和极小(Minima)序列Fig.3 The maxima (upper) and minima (lower) return series obtained for R=4 over the whole period

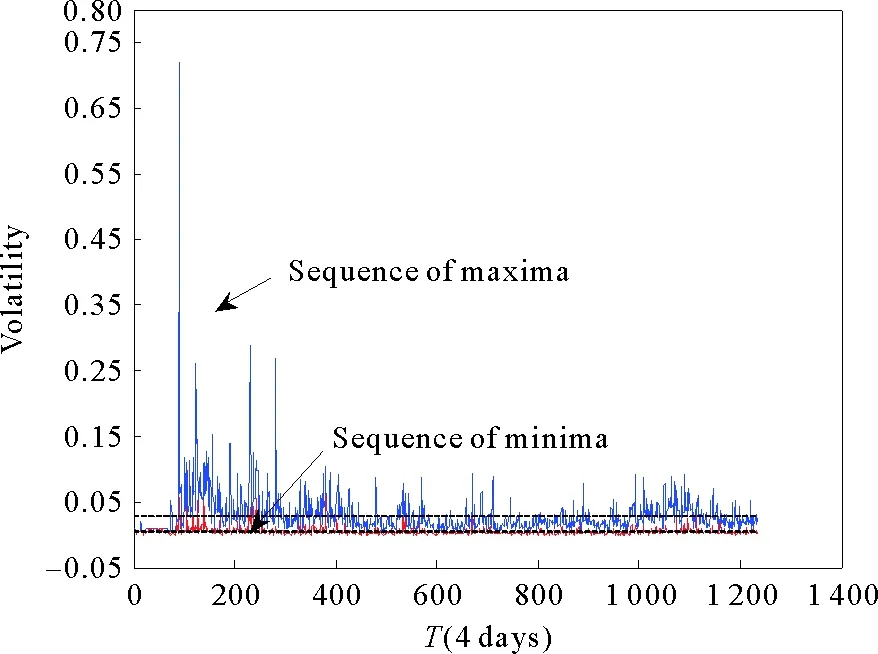
图4 R=4时波动率序列的 极大(Maxima)和极小(Minima)序列Fig.4 The maxima (upper) and minima (lower) volatility series obtained for R=4 over the whole period

图5 收益最大值(Maxima)，收益最小值(Minima)， 收益率(Returns)和波动率(Volatility)的自相关函数Fig.5 The autocorrelation function for the maxima of returns, minima of returns, returns and volatility

3.2 极值收益率序列的长记忆性特征

更进一步地，为了量化这种长记忆性，以上海股票市场为例，我们分析整个样本区间上的上证指数序列极大值和极小值的收益率序列和波动率序列。首先，我们分析了4个不同序列的自相关函数。这些序列包括R=1时的收益率序列和波动率序列，以及R=4时的极大值和极小值序列。图5分别给出了自相关函数的实证分析结果。从图5可以清楚地看出，当R=4时的极大值和极小值序列的自相关函数以一种幂率形式逐渐衰退，且该幂率指数约为-0.3。从图5也可以看出极大值及极小值的衰减与波动率自相关函数的衰减类似，但是与收益率自相关函数(在此时间范围内趋于0)的衰减却大不相同，上述结果印证了文献[27]的结论。

然而，自相关函数具有其局限性。自相关函数往往被认为容易受到数据顺序及时间趋势的影响。检验长记忆性的另一种常见的方法是R/S分析[3-4]。R/S分析方法最早由英国水利学家Hurst提出，Hurst在大量实证研究的基础上提出了一个统计量H来识别这一系统性的非随机特征，即Hurst指数，其具体步骤如下：

1)定义长度为N的收益序列{Rt}，并将它分割为长度为n的A个连续子区间。将每一子区间标为Ia,a=1,2,…,A。于是Ia中每一点可以表示为Rk,a,k=1,2,…,n;a=1,2…A。

2)对每一长度为n的子区间Ia，计算其均值为：

(1)

对单个子区间计算其累积均值离差Xk,a：

(2)

3)由式(2)可知，单个子区间累积均值离差序列{X1,a,X2,a,…,Xn,a}之和为零。定义单个子区间的极差为：

RIa=max(Xk,a)-min(Xk,a),k=1,2…n

(3)

4)计算每一子区间的标准差SIa，并用它对极差进行重标度/标准化(RIa/SIa)：

(4)

5)因此，对划分长度n，可以计算A个子区间平均的重标度极差：

(5)

6)对不同的划分长度(即不同的时间尺度)n重复以上计算过程，可以得到多个平均重标度极差值。log(R/S)与log(n)存在线性关系：

log(R/S)n=a+Hlog(n)

(6)

7)对n和R/S进行双对数回归，其斜率就是长程相关的参数，即Hurst指数H。因此，可以通过普通最小二乘法得出序列的长程相关参数H。

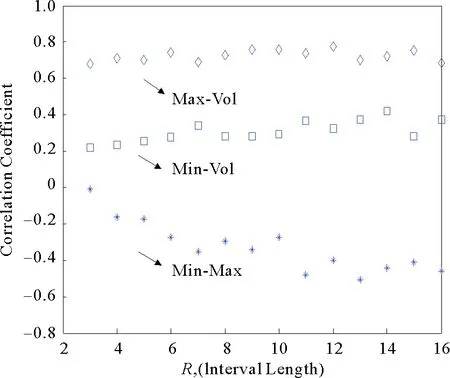
Hurst指数不但能够从分形时间序列中区分出随机时间序列，并能够在此基础上进一步判定该序列是持久性序列还是反持久性序列：当H=0.5时，该过程是一个独立同分布过程；当0.5

根据公式(1)-(6)，对上述提到的序列(收益率序列、波动率序列、当R=4时的极大值序列以及极小值序列)进行R/S分析。实证结果如图6和图7所示。从图6和图7可以看出，所有的序列均具有显著的长记忆性，因为它们的系数均大于0.5。此外，从图6中可以看出，波动率序列比收益率序列表现出更强的长记忆性，因为波动率序列的Hurst指数值明显高于收益率序列的Hurst指数值。同样，如图7所示，极小值序列和极大值序列呈现出类似的明显的长记忆性特征。

此外，应该提及的是R/S方法往往容易高估某些时间序列的Hurst指数。对于通过R/S分析得出的Hurst指数应该谨慎一些[29]。因此，采用另外一种方法研究4个不同序列的长记忆性，即消除趋势波动分析方法[5](DFA)。DFA方法本身具有一定的优势，比如该方法可以平滑消除原始数据的局部趋势，更容易检测出局部相关性，该方法的具体计算步骤如下：

对给定长度为N的序列{xi}，i=1,2,…,N，DFA方法的一般过程如下：

1)通过求和把原序列归并成一个新的序列：

(7)

2)把序列yi分割成长度为s的Ns=int(N/s)个互不相交的等长区间，由于长度N经常不是s的整数倍，为了不丢弃尾部剩余部分，从序列尾部重复这一分割过程，因此得2Ns区间。

3)通过最小二乘法拟合每一子区间v(v=1,2,…,2Ns)上的局部趋势pv(j)函数消除子区间v中的局部趋势序列：

Zv(j)=yv(j)-pv(j) (j=1,2,…,s)

(8)

4)分别计算2Ns个消除趋势子区间序列的平方均值：

(9)

这里v=1,2,…,Ns，进而求出这2Ns个F(s,v)的均值平方根：

(10)

5)在双对数图中分析波动函数F(s)与s的如下关系：

F(s)∝Sα

(11)

对每一个分割长度s，可求出相应的一个波动函数值F(s)，作出Ln(F(s))～Lns函数关系图，其斜率为标度指数α。α体现了序列的相关特性：当α=0.5，意味着该序列不存在长记忆性。若时间序列仅是短期相关，α值会十分接近于0.5；当0.5<α≤1，说明时间序列具有状态持久性，即该序列存在长期记忆特征，当前的事件和未来事件之间存在长程相关性；当0<α<0.5，时间序列具有状态反持久性，即如果一个时序在前一个期间存在一个向上(下)趋势，则它在后一个期间很可能存在向下(上)的趋势。

采用DFA方法，依次对上证指数4种不同的序列进行消除趋势波动分析，其实证结果如图8所示。在图8中列示的是当时间间隔为R=4时的收益率和波动率序列。更详细地，图9给出了R=4时极大值序列和极小值序列的DFA结果，图10给出了R=4时收益率序列和波动率序列的DFA结果。

图6 收益率序列和波动率序列的R/S分析Fig.6 R/S analysis of returns and volatility for SHSI

图7 极大值序列和极小值序列R/S分析Fig.7 R/S analysis of minima and maxima records for SHSI

图8 收益率、波动率、极小值和极大值序列的DFA分析Fig.8 Detrended fluctuation analysis of returns, volatility, minima and maxima records for SHSI

图9 当R=4时极小值和极大值序列DFA分析Fig.9 Detrended fluctuation analysis of minima and maxima records for SHSI, for R=4

从图9中可以看出，极大值序列和极小值序列的DFA指数分别为0.576 4和0.772 2。这表明当R=4时极大值序列和极小值序列均具有显著的长记忆性，因为它们的系数均大于0.5。此外，从DFA指数可以看出，与极大值序列相比，极小值序列显示出更强的长记忆性。与此类似，如图10所示，收益率序列和波动率序列的DFA指数分别是0.551 7和0.875 8，表明这两个序列均具有长记忆性。此外，波动率序列长记忆性比收益率序列的长记忆性更显著。所有这些结果都与R/S分析的结果相一致，该结果进一步证实了极值收益率长记忆性特征的存在。

图10 R=4时上证指数收益率和波动率 序列的消除趋势波动分析Fig.10 Detrended fluctuation analysis of returns, volatility records for SHSI,for R=4

为了估计极值收益率序列所包含信息与相应波动率序列包含信息之间的相关程度，我们进一步分析极大值和相应的波动率、极小值和相应的波动率以及极大值和极小值序列之间的互相关关系。图11给出了随时间间隔R变化的互相关函数的趋势图。从图11中可以看出，极大值和相应的波动率之间的互相关系数总体保持稳定，且其互相关系数值均大于0.6，说明极大值和相应的波动率之间的相关性较强，此外，极小值与相应的波动率之间的互相关系数也总体保持稳定，且其互相关系数值介于0.2到0.4之间，说明极小值和相应的波动率之间也具有一定的相关性，但相比极大值，极小值和相应的波动率之间相关性较弱。然而随着R的增加，极大值和极小值序列的相关系数逐渐减小且几乎所有系数都小于或等于0。换句话说，极大值和极小值序列呈负相关且这种负相关随着R的增加变得越来越强。如图12所示，我们也分析了极值(极大值和极小值)与收益率之间的互相关系数，得到了类似的结论。

图11 极值(极大和极小)和波动率序列间的互相关系数Fig.11. Coeffients of cross-correlation between the series of extrmes(maxima and minima) and volatility

图12 极值(极大值和极小值)和收益率之间的互相关系数Fig.12. Coeffients of cross-correlation between the series of extremes (maxima and minima) and return

4 结论

本文聚焦于金融市场极端波动行为，以中国股票市场最具代表性指数——上证指数为研究样本，将金融市场按照一定期间划分为不同的时间窗口，将每个时间窗内的极值收益率组成一个时间序列，并将该极值收益率序列作为实证研究对象，分别运用自相关函数、重标极差分析(R/S)方法、消除趋势波动分析(DFA)方法等复杂性方法综合对极值序列(包括极大值序列、极小值序列、收益率序列以及波动率序列)的长记忆性进行了检验，实证研究发现收益率序列和波动率序列均具有长记忆性；同时发现极值序列也呈现出显著的长记忆性特征，且与相应的波动率序列相似。此外，进一步分析了极大值和相应的波动率、极小值和相应的波动率以及极大值和极小值序列之间的相关函数的变化特征，统计结果同样证实了极值序列的长记忆性特征，这些研究均表明极值序列具有持久性的趋势。本文的实证研究结果能够帮助我们更好的理解股票价格动态波动的性质。然而，极值序列的动态行为特征和变化机理还有待进一步研究。如何深刻认识金融市场极端事件的复杂特征以及如何揭示关于市场变化的更多有价值的信息是未来有待解决的两个关键问题。对于这些问题的研究将有助于金融风险的防范和控制。