培养学生的逻辑推理能力
2020-05-06周海艳
周海艳
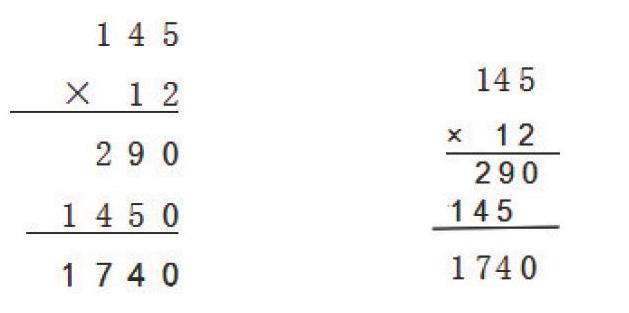
课堂教学应激发学生的学习兴趣,引发学生的思考,鼓励学生创造性思维,帮助他们掌握基本的知识技能、思想方法,获得丰富的数学经验。如何立足于学生的“学”,着眼于学生逻辑推理能力的提升,帮助学生理解三位数乘两位数的算理呢?
一、 复习旧知,导入新课
在课堂上,教师可以先引导学生复习旧知识,逐步导入新知识的学习。
教学《三位数乘两位数》时,笔者先出示“14×2=( )”和“14×12=( )”,问学生能不能很快地算出得数。第一道题,学生直接口算出了结果。第二道题,一名学生用推理的方法推出得数是168,即把12分成10和2,先用14×2=28,再用14×10=140,最后用140+28=168;另一名学生说,还可以列竖式计算。教师指名学生板书演示,要求全班学生一起笔算,算完后说说在计算的过程中的想法。
复习引入时不宜贪多求全,教师在基础知识上下足工夫,将多位数乘一位数、两位数乘两位数的计算方法做实做细,为接下来的教学打下了坚实的基础。
二、自主探究,明白算理
计算教学,引导学生明白算理很重要,因为算理解决的是“为什么这样做”,实际计算过程解决的是“怎样做”。“为什么这样做”是思维层面的问题,“怎样做”是技术层面的问题,思维层面的问题解决了,技术层面的问题解决起来也就相对容易一些。
教学中,笔者先出示一个问题:从谷城县乘动车去北京大约需要12小时,火车速度每小时145千米,从谷城到北京有多少千米?怎样列式?为什么这样列式?用乘法计算这道题并不是这节课的教学点,因为这是学生以前已经掌握的知识,这节课的重点是解决怎么计算的问题。学生根据“路程=速度×时间”列出“145×12”后并尝试计算。教师问学生是怎么算的,大部分学生采用的是估算法,如把145估成150,把12估成10,也有学生把12拆分成10和2,或者2×6、3×4,个别学生采用了列竖式的方法计算。教师展示了两名学生的计算结果(如下图):
师:两种不同的方法,结果是一样的,大家喜欢哪种方法,为什么?
生1:我喜欢第二种。用个位上的2去乘第一个因数,结果等于290,表示2个290是多少;然后用十位上的1去乘第一个因数,表示145个10是多少,最后把两个数的积相加。
师:第一步算得的积是290,它表示的是几小时行驶的路程?第二步算得的积的末尾为什么要与十位对齐呢?它表示的又是什么意思?
生1:290表示2小时火车行驶的路程。第二步是用第二个因数12十位上的1和145相乘,表示145個10,表示10小时火车行驶的路程,这里的0省略了,不需要写。
师:回忆一下刚才的计算过程,和以前学习的两位数乘两位数的方法有哪些相同之处和不同之处?列竖式时需要注意什么?
生2:我认为相同之处是用第二个因数的个位分别去乘被乘数的每一位,末尾和个位对齐。
生3:我认为相同之处是两位数乘两位数、三位数乘两位数,都是用十位上的数去乘第一个因数,末尾和十位对齐;不同之处就是三位数乘两位数比两位数乘两位数多乘一个百位上的数字。
生4:我认为它们的方法都是一样的,都是用第二个因数的个位去乘第一个因数的每一位数,末尾和个位对齐,再用第二个因数的十位去乘第一个因数的每一位,末尾和十位对齐,最后把两个数的积相加。
本节课的难点是用十位上的数去乘第一个因数的每一位,积的末尾和十位对齐。为了突破这一难点,笔者注重了知识的迁移,即引导学生对比学过的三位数乘一位数、两位数乘两位数和三位数乘两位数的算理,找出它们的相同之处和不同之处。通过对比,学生很快总结出了三位数乘两位数的计算方法。
三、 巩固练习,拓展提升
巩固提升阶段,笔者设置了闯关答题。第一关:计算358×28和563×46的积。第二关:判断出哪个结果一定是错误的。①121×13=484;②121×13=1573。第三关:解决下面这个问题:学校要为各班新购买一套百科全书,售价129元∕套,全校共36个班,购买这些新书一共要花多少钱?在第二关,很多学生一眼就看出第①个一定错了,因为只从个位就能看出,计算结果的最后一位数应该是3。另一名学生说,把121看成100,把13看成10,积应该比1000大,所以第①个一定是错的。
(作者单位:襄阳市谷城县粉阳路小学)
