在深度学习中生成核心能力

王华蓉

近日，笔者应邀在《湖北教育》第一届“教研名师”观摩课暨中小学生发展核心素养研讨活动中主讲了观摩课——《平行四边形的面积》。笔者从生活问题入手，引导学生经历观察、猜想、验证、转化、对比、迁移、推理、总结、应用等数学活动，获得平行四边形面积的计算方法，走向深度学习。

一、渗透思想方法

一是转化、等积变形思想方法的渗透。数学思想方法是处理数学问题的指导思想和基本策略，是数学教学的灵魂。引领学生探究平行四边形的面积计算公式时，教师要有机地把“数方格”的方法和转化方法融为一体。

教学中，教师先用课件出示七巧板拼图（图1），得出规则的正方形的面積后，再出示两个不规则的拼图（图2，图3），问：“这两个图案的面积是多少？”学生通过观察发现：图2、图3是把规则的拼图转化为不规则的拼图，形状变了，但面积不变。

接着，教师出示方格图（图4），提示学生，每个方格的面积为1平方厘米，不足一格的按半格计算，要求学生数出两个不规则图形的面积。学生数完后，教师展示学生数方格的方法，引导他们进一步感悟把不规则的图形转化成规则图形的转化方法。

二是空间观念的培养。引导学生自主探究“平行四边形的面积”中，教师不但要让学生悟出把方格纸剪下来拼一拼，将不是整格的拼成整格，再数出平行四边形面积的方法，还要让学生通过画一画、剪一剪、移一移、拼一拼等方法，创造性地将平行四边形转化成长方形求面积，在变与不变中感受转化方法，培养和发展空间观念。教学中，教师先让学生通过比较，发现长方形的长与原平行四边形的底相等，长方形的宽与原平行四边形的高相等，然后通过小组交流，推导、归纳出“平行四边形的面积=底×高”。这样教学不仅充分发挥了学生的主体作用，而且培养了学生的创新意识和空间观念，提升了学生分析、综合、比较、抽象和概括的能力。

二、充分体验操作

核心素养下的课堂关注的是学生的体验与感悟，以及知识背后所蕴含的数学价值。

当学生猜测“平行四边形的面积=底×高”后，教师让学生说说猜想的依据，然后引导他们去探索，去研究，去经历知识的获得过程。课前，教师给学生准备了大小不一的平行四边形。课中，学生动手前，教师先引导他们思考：①你通过剪、拼，将平行四边形转化成了什么图形？②你是怎样剪、拼的？你是沿着什么剪的？学生操作的过程中，教师提示学生关注：“为什么要沿着高剪开，并且平移？”学生通过观察、思考，发现要转化为长方形，四个角必须都是直角，并且平移后两腰重合才能保证底边长不改变。学生在经历、体验、思考、分享的过程中，思维不断生长，最终将新知转化成旧知，根据长方形的面积计算公式推导出了平行四边形的面积计算公式。

三、精心设计问题

问题是思维的起点。教学中，教师要精心设计问题，让数学学习变得有深度。

引导学生推导平行四边形的面积计算公式时，教师先提出问题：“把平行四边形剪拼成长方形，应该怎样剪？”学生经过思考，有的从左边顶点往对边剪，有的从右边顶点往对边剪。这是一般性的思维。教师再提出问题：“沿中间的某一个点往对边剪，可以吗？”当学生将手中的平行四边形转化成长方形后，教师又提出问题：“平行四边形转化成长方形后，什么变了？什么没变？转化后的长方形的长和宽与原来的平行四边形的底和高有什么关系？”学生经过思考和辨析，知道平行四边形转化成长方形后，面积不变，形状变了，转化后的长方形的长和原来平行四边形的底相等、宽和原来平行四边形的高相等，进而根据长方形的面积公式推导出“平行四边形的面积=底×高”。教师追问“是不是所有的平行四边形都能转化成长方形”，并播放不同形状的平行四边形转化成长方形的微课，让学生观察、感悟、思考，明白所有平行四边形的面积都可以用“底×高”来计算。学生经历由特殊到一般的推理过程，在变中找到了不变：“因为平行四边形的高有无数条，所以有无数种剪法;因为要剪拼成长方形，所以要沿高剪。”这样的引导，使学生深刻认识到平行四边形的面积与它的高有关。在此基础上引导学生推导出平行四边形的面积计算公式，自然就水到渠成了。同时，学生也发现所有平行四边形的面积都可以用这个公式来计算，思维走向了更高的台阶。

四、适时引导思辨

学生经历数学学习活动后，教师要引导他们思辨，让其从学习活动中提炼出一些学习经验，将感性认识上升为理性认识。

为什么会出现第一种算法呢？学生说，因为长方形的面积等于长乘宽，所以平行四边形的面积也可以用邻边相乘的积计算。“平行四边形的面积是不是可以用邻边相乘来计算？”教师以问题为内驱力，拨动学生的思维之弦。学生通过小组交流，发现平行四边形的面积只能用相对应的底和高相乘。

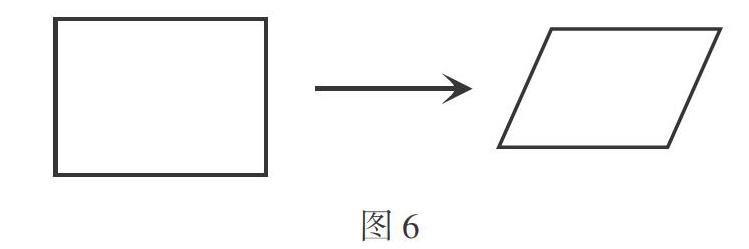
又如：如图6，把一个长方形框架拉成平行四边形，平行四边形和原来的长方形相比，面积变了吗？

当这个问题呈现时，学生一下子得出两种结果：“面积变小了”;“面积没有变”。哪种结果对，为什么呢？学生思考后发现：平行四边形的面积大小与它的底和高的大小有关。把长方形拉成平行四边形后，虽然底没变，但是高变小了，所以面积变小了，但它的周长没有变。这种思辨，让学生进一步感悟了转化的数学思想方法，加深了对几何图形特征的认识和理解，提升了数学思维能力和空间想象能力。

（作者单位：武汉市光谷第21小学）

责任编辑  姜楚华