改进的基于灰度级的模糊C均值图像分割算法
2020-05-06赵战民朱占龙王军芬
赵战民,朱占龙*,王军芬
(1.河北地质大学 信息工程学院,河北 石家庄 050031;2.河北地质大学 人工智能与机器学习研究室,河北 石家庄 050031)
1 引 言
图像分割是图像处理中的关键任务之一,其目的是将图像划分为两个或更多的区域[1]以进行后续的识别、测量等工作。现存在众多分割算法能有效对图像进行分割,其中基于模糊C均值(Fuzzy C-means, FCM)算法[2-8]是一种较经典的图像分割算法。
为提升算法的鲁棒性,研究人员提出了许多FCM算法的改进版本。按照算法的执行框架,可以将这些改进算法分为两类:一类是基于图像像素的图像分割算法,具体是将每个像素单独考虑,按照最终隶属度大小对图像进行分割[2-4],如典型的结合邻域信息的FCM(Fuzzy Local Information C-means, FLICM)[3]以及结合非邻域空间信息的FCM(Fuzzy C-means with Non-local Spatial Information, FCM_NLS)[4]。这类算法通过在目标函数中引入像素的邻域或者非邻域信息提升了算法的鲁棒性;另一类是基于图像灰度级的分割算法[5-8],与第一类不同之处在于,为保证算法鲁棒性,首先要对图像进行去噪,常见的有基于像素邻域平均法[5]以及同时考虑像素邻域值和邻域位置方法[6]对图像去噪。该类方法在降噪图像的基础上生成灰度直方图,再将灰度级以及相应灰度级的个数一起考虑进行聚类分割。因为灰度级个数远小于图像像素个数,进而导致图像分割速度明显加快。
无损检测图像一般由超声检测、涡流检测等手段对材料或工件进行检测而得,通过图像分割能够发现材料或工件表面和内部的缺陷,也能进行尺寸测量与识别。无损检测图像因为易受到干扰而清晰度较差且往往呈现出灰度分布不均衡的特点[9]。FCM的改进算法诚然提升了算法鲁棒性,但它们分割不均衡特性的图像效果较差,其根本原因在于它们总是趋于均分图像像素[10],这是由于算法的目标函数所导致,因此有必要对目标函数进行改进。文献[10-11]针对数据不均衡问题对目标函数进行了改进,但后续并未进行严格推导且未能推广至图像分割领域。
针对无损检测图像呈现出的灰度分布不均衡的状况,本文在基于灰度级的模糊C均值框架基础上设计新算法,在继承该框架运行速度快的优势的同时也能够有效分割无损检测图像。本文算法设计了每一类隶属度之和的表达式并将其引入至基于灰度级模糊C均值的目标函数中,进而得到了新的隶属度和聚类中心表达式,随后考虑了类紧密度对聚类进程的影响并给出新算法的执行步骤,最后利用具有灰度分布不均衡特性无损检测图像对本文算法进行分割测试,结果表明本文算法能够对无损检测图像进行有效分割。
2 相关工作
2.1 基于灰度级的模糊C均值目标函数及迭代公式
基于灰度级的模糊C均值算法的目标函数如下:
(1)
其中:vi(1 ≤i≤c)为聚类中心,N表示图像的像素数,γl表示灰度级l的像素数,m是模糊指数,uil表示灰度级l属于第i类的隶属度,ζ表示去噪后的图像。由拉格朗日乘子法最小化式(1),可得:

(2)
(3)
基于灰度级模糊C均值算法的执行过程参见文献[6]。
2.2 典型图像去噪方法
Cai等人提出了一种有效的图像去噪方法[6],具体表示为:
ζj=∑i∈NjSijxi/∑i∈NjSij,
(4)
(5)
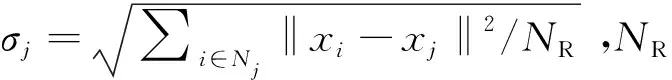
3 本文算法
3.1 目标函数的改进
由于目标函数的限制导致基于灰度级的快速模糊C均值算法仍趋于均分待分割图像的所有像素。如果待分割图像灰度分布不均衡,这类算法很容易造成图像分割失败[10],这便需要对目标函数进行改进,如下所示:
(6)
对式(6)进行改写,如下:

(7)
由式(7)可以看出,当第i类为较大类时,式中除数也较大,故采用上式可以弱化较大类对目标函数的贡献,从而避免使得较小类的聚类中心向较大类靠拢,造成分割效果较差。另外,需指出,该式的约束条件与式(1)保持一致。采用拉格朗日乘子法对式(6)优化,首先构造如下拉格朗日辅助函数:

(8)

(9)

由式 (9)可得:
(10)


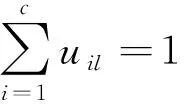
(11)
将式(11)代入式(10)可得:
(12)


(13)
则 式(12)和 式(13)为新的隶属度和聚类中心表达式。
3.2 类的紧密度
除了类的大小对聚类结果存在影响外,类的紧密度(密度)对聚类结果也有较大作用。显然,如果某一类具有较大的紧密度,那么我们希望在聚类过程中提升该类对聚类结果的影响,反之亦然。本文基于灰度级的模糊C均值框架设计了类的紧密度表达式如下:
(14)
其中:
Si={ζl|uil>upl;p=1,2,...,c;p≠i},
(15)
(16)
式(14)~(16)中,γl仍为像素灰度级为l的个数,Si表示第i类像素组成的像素集,|Si|表示该类像素集的数目,μi表示第i类像素与聚类中心vi距离的平均值。Ii值越小反映出该类具有越高的紧密度,表明第i类的像素属于该类的可能性越高,反之亦然。为了在类与类之间做一个横向对比,采用下式处理:
fi=(1-Si)/(1-Smin),
(17)
其中:
(18)
Smin=min{Si,i=1,2,...,c},
(19)
需要指出,式(17)中的fi定义为相对的紧密度系数。由式(17)~(19)可以看出,如果某类具有较高的系数,则说明该类的像素灰度值分布较为紧凑,将此系数融入至聚类进程能够提升聚类精度,公式如下:
(20)
3.3 本文算法的执行步骤
本文算法的执行流程描述如下:
输入:聚类中心数c,模糊指数m,参数λs、λg,最大迭代次数T,终止条件ε;
(1)利用式(4)对原图像进行去噪得到图像ζj;
(2)利用去噪图像得到相应的灰度直方图ζl;
(3)随机初始化聚类中心V0;
(4)Forq= 1∶Tdo
(5)按照式(2)利用V(q-1)计算隶属度Uq;
(6)将类的大小引入至隶属度,即更新Uq,如式(12)所示;
(7)将类的紧密度引入至隶属度,即更新Uq,如式(20)所示;
(8)由新的隶属度更新Vq,如式(13)所示;
(9)If ‖Vq-Vq-1‖<ε或q>T,then执行12;
(10)End if
(11)End for
(12)输出U,由此判决灰度级ζl对应的类,得到分类结果。
4 实验与结果
4.1 实验参数设置及说明
为了测试本文算法对无损检测图像的分割效果,选用F_value评价指标[11]来评价其分割效果,其表达式如下:
(21)
其中P为查准率,R为查全率,β为度量P和R的相对重要性。该指标能够有效评价具有灰度分布不均衡特征图像的分割结果,其值越大表示分割效果越好。将本文算法与其他基于灰度级的模糊C均值算法进行比较,如增强FCM(Enhanced Fuzzy C-means, EnFCM)算法[5]、快速广义FCM(Fast generalized fuzzy C-means, FGFCM)算法[6]、文献[7]算法和FNDFCM_P(Fast noise detection fuzzy C-means and post-processing, FNDFCM_P)算法[8]。之所以与这些算法进行比较,是因为这些算法都是基于灰度级的快速模糊C均值算法,相比较基于像素的模糊C均值算法具有明显的速度优势,同时这些算法在各自的论文中都取得了显著的分割效果。因此,在后续的分割实验中对比算法的参数皆来自相应论文的推荐值,各算法的参数设置如表1所示。实验环境为:Matlab (R2014a)、3.40 GHz Intel®CoreTMi3-2130处理器,2 GB内存,Windows7中文版操作系统。

表1 算法参数设置Tab.1 Parameters setting of these algorithms
选择无损检测图像(分别命名为#NDT1~#NDT5)进行分割试验且所选择的图像具有标准分割结果,有利于对算法进行定量评价。图1给出了原图像、对应的标准分割图像和灰度直方图。通过灰度直方图可以看出,所选择的无损检测图像都具有灰度分布不均衡的特点。

(a)~(e) 原图像 (#NDT1~#NDT5)(a)~(e) Original images (#NDT1~#NDT5)

(f)~(j) 标准分割图像 (#NDT1~#NDT5)(f)~(j) Standard segmented images (NDT1~NDT5)

(k)~(o) 灰度直方图 (#NDT1~#NDT5)(k)~(o) Gray-level histograms (#NDT1~#NDT5)图1 原图、标准分割图及灰度直方图(#NDT1~#NDT5)。Fig.1 Original images, standard segmented images and gray-level histograms(NDT1~NDT5).
4.2 分割结果
图2~6展示了各算法对无损检测图像在高斯噪声(归一化方差0.01)干扰下的分割结果。另外,为了测试算法的适应性和鲁棒性,对图像在其他噪声水平干扰下进行了分割实验,测试结果如表2所示。由图2~6展示的可视分割结果与各自的标准分割图像(图1(f)~(j))相比对可以看出,所提出的算法能够有效地对具有灰度分布不均衡的图像进行有效分割,而其对比算法由于没有考虑图像灰度分布不均衡特性,分割效果较差。另外也可以看出,文献[7]算法的抗噪性最强,但存在边缘模糊现象,这是此种算法的去噪特性决定的。由表2的指标值F_value可以看出,所提出的算法分割结果最好,说明了本文算法对基于灰度级的模糊C均值算法的目标函数进行改进是有效的,它继承基于灰度级聚类的速度优势的同时,改善了模糊C均值算法总是趋于均分图像像素数目的缺陷。

图2 #NDT1图像在高斯噪声(归一化方差0.01)干扰下的分割结果Fig.2 Segmentation results of #NDT1 with Gaussian noise (0, 0.01) based on thesealgorithms

图3 #NDT2图像在高斯噪声(归一化方差0.01)干扰下的分割结果Fig.3 Segmentation results of #NDT2 with Gaussian noise (0, 0.01) based on these algorithms

图4 #NDT3图像在高斯噪声(归一化方差0.01)干扰下的分割结果Fig.4 Segmentation results of #NDT3 with Gaussian noise (0, 0.01) based on these algorithms

图5 #NDT4图像在高斯噪声(归一化方差0.01)干扰下的分割结果Fig.5 Segmentation results of #NDT4 with Gaussian noise (0, 0.01) based on these algorithms

图6 #NDT5图像的高斯噪声(归一化方差0.01)干扰下的分割结果Fig.6 Segmentation results of #NDT5 with Gaussian noise (0, 0.01) based on these algorithms
表2 对#NDT1~#NDT5图像各算法的分割指标(F_value)对比
Tab.2 Indexes(F_value) comparison of different algorithms on #NDT1~#NDT5 images with different noise

Image噪声水平EnFCMFGFCMRef.[7] 算法FNDFCM_PIFCMG# NDT1Gaussian noise(0,0.01)0.429 10.416 30.473 20.402 70.644 9Gaussian noise(0,0.02)0.400 20.409 10.488 20.365 10.625 3Salt &Pepper noise(0.1)0.409 00.531 20.449 90.374 40.734 3Salt &Pepper noise(0.2)0.336 50.435 10.384 20.398 50.623 6# NDT2Gaussian noise(0,0.01)0.757 70.771 50.836 90.630 40.935 0Gaussian noise(0,0.02)0.638 00.668 70.818 90.574 50.907 6Salt &Pepper noise(0.1)0.604 40.782 20.827 60.633 40.942 9Salt &Pepper noise(0.2)0.446 40.669 00.720 20.576 20.878 6# NDT3Gaussian noise(0,0.01)0.657 20.679 70.795 20.584 80.911 8Gaussian noise(0,0.02)0.551 00.567 70.667 60.502 00.822 7Salt &Pepper noise(0.1)0.556 30.804 50.624 50.577 70.923 0Salt &Pepper noise(0.2)0.480 60.653 80.606 00.552 60.830 3# NDT4Gaussian noise(0,0.01)0.887 20.895 70.928 00.866 70.941 6Gaussian noise(0,0.02)0.841 80.861 00.910 40.826 20.913 1Salt &Pepper noise(0.1)0.835 00.903 30.913 40.863 60.941 0Salt &Pepper noise(0.2)0.755 00.846 80.874 10.831 60.899 4

续 表
4.3 综合性(鲁棒性)分析
采用公式(22)评价本文算法的鲁棒性[12]:
(22)
其中:n表示算法个数,Ri表示算法i在某幅图上的相对分割表现,其值越高,越表明算法i在某幅图上的分割效果越好,取值范围为(0,1]。
将表2中各算法的指标按照式(22)进行调整得到Ri值并进行累加,可得算法i的综合分割表现,即算法的鲁棒性。累加的结果如图7所示,显然,所提出的算法具有最高的鲁棒性,比其他算法分别高出4.43,2.79,2.33,4.26,折合百分比分别为26.13%,16.46%,13.75%,25.10%。
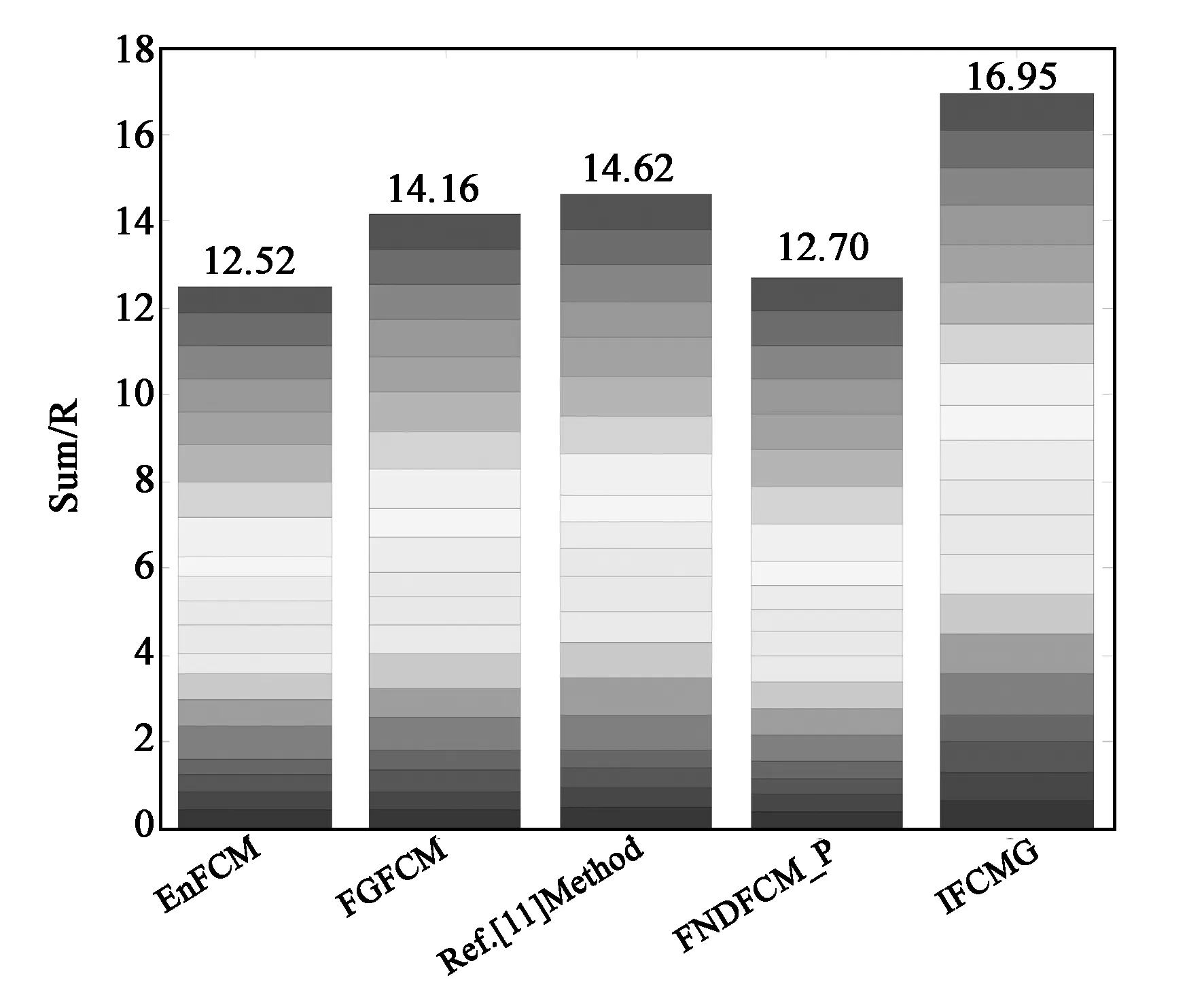
图7 算法鲁棒性分析Fig.7 Robustness of these algorithms
5 结 论
本文提出一种快速的基于灰度级的模糊C均值图像分割算法。无损检测图像具有灰度分布不均衡的特征,将能够表征灰度分布不均衡特性的类隶属度表达式融入至基于灰度级的模糊C均值算法目标函数并将其严格推导。同时,为了度量类的密度对聚类的影响,设计基于灰度级的类紧密度并将其融入迭代进程。采用本文算法和对比算法对添加了不同水平噪声的无损检测图像进行分割实验并采用F_value指标进行算法衡量。最后利用综合评价公式对所有的F_value值进行算法综合评价,结果显示,本文算法的综合评价值比其他对比算法分别高出26.13%,16.46%,13.75%,25.10%,显示了本文算法分割的有效性和鲁棒性。
