人眼可感知最多相邻像素灰度差的全局图像优化方法*
2020-06-19蔡铁峰
蔡铁峰
人眼可感知最多相邻像素灰度差的全局图像优化方法*
蔡铁峰
(深圳职业技术学院 教育技术与信息中心,广东 深圳 518055)
图像优化可以使图像内更多面向探测识别的信息被人眼感知.现有的图像优化方法缺少合理的量化指标,图像没有做到面向人眼探测识别最优,甚至优化后图像人眼可探测识别的景物信息会减少.本文基于图像中景物轮廓与纹理信息主要体现为相邻像素灰度差的认识,以图像中最多相邻像素对灰度差人眼可感知为量化指标,设计全局图像优化快速算法.实验表明,与现有的全局图像优化方法比较,本方法优化后图像有最多的相邻像素灰度差人眼可感知,某种意义上使图像面向人眼探测识别最优.
探测识别;图像优化;对比度增强
在灰度图像中,人眼探测识别主要依赖景物的轮廓与纹理信息,景物轮廓与纹理主要体现在相邻像素间的灰度差上.当相邻像素间灰度差小,由于人眼视觉特性,人眼将感知不到此灰度差,也就感知不到相关的景物信息.随着手机摄像头等成像设备采集能力的进步,图像面向人眼探测识别可优化的空间越来越大.图像优化拉伸图像对比度,使图像内信息更多被人眼感知,并且图像优化方法研究成果也可以用来指导成像系统设计.
灰度图像优化方法在空间域内可以粗略地分为两类:全局方法和局部方法.全局方法对整幅图像进行灰度级拉伸,具有运算简单快速的特点.局部增强方法放弃全局性约束,由局部区域图像灰度值确定每个像素的灰度值,能更大拉伸相邻像素间灰度差,但可能会出现一定程度的图像失真.全局方法研究是局部方法研究的基础,在全局方法的基础上可以衍生出局部方法.
现有的以直方图均衡(HE)、线性拉伸(LS)、分组直方图均衡(GLG)为代表的常见全局方法都没有明确且合理的量化目标,停留在图像增强阶段,没有使图像做到最优,甚至出现增强后的图像不如原图的情况.OCTM方法[1]以及文献[2-3]基于直方图定义图像全局对比度量化指标,此类量化指标在图像二值化时反倒取值最优,相应的算法虽添加约束避免二值化,但没有根本上解决不合理优化目标的天然缺陷.另外一些优化方法基于信息论以直方图互信息[4]或信息熵作为量化指标[5-9],把人眼感知信息视为一个信息传输过程.这些量化指标都是泛泛地定义在直方图上,没有直接定义在图像相邻像素之间灰度差上,没有和人眼探测识别直接关联起来.本文在以全局灰度级不倒序约束保真图像信息约束下,以图像中最多相邻像素灰度差被人眼可感知为优化目标,设计快速算法得到最优的那幅图像.
1 问题定义与求解策略
全局图像优化方法是一个灰度级映射过程,灰度级映射有可能改变图像信息.本文方法采用全局不倒序为图像保真约束,本约束要求灰度级在映射过程中大小关系不发生逆转.对于灰度图像,人眼探测识别依赖景物的轮廓与纹理信息,景物轮廓与纹理主要体现在相邻像素间的灰度差上.以没有先验知识为前提,可以认为每对存在灰度差的相邻像素间对都包含一个单位的探测识别信息.故本文在全局不倒序约束下,使图像中灰度差人眼可感知相邻像素对的数量最多,在某种意义上使图像面向人眼探测识别最优.
1.1 图像优化问题的数学定义
相邻像素间灰度差小时,由于视觉特性,人眼将感知不到此灰度差,为了便于量化计算,可认为存在人眼感知灰度差的阈值.相邻像素灰度差大于阈值时人眼才感知到灰度差.人眼感知相邻像素对灰度差受背景光强度、纹理构型等复杂因素影响,本文采用一种不完善但简洁的灰度差阈值表达(参见式16),此表达是由实验数据拟合[10,11].令变量是一个灰度级,返回值()是其他灰度级与的差能被人眼感知到的灰度差阈值.不同的灰度级对应的灰度差阈值不同,人眼感知灰度差的非均匀性给图像优化带来困难.


则本文优化问题数学定义为:
优化目标:

约束条件:
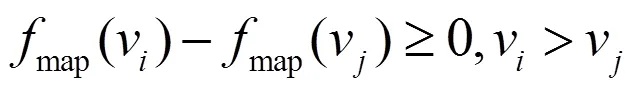
1.2 求解策略
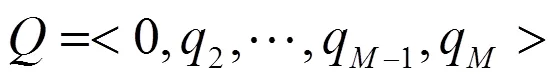
假设我们已经通过把灰度级序列映射到得到那幅最优图像.在此前提下,把灰度级序列根据式(4)映射到序列中.序列中多个灰度级可以映射到中同一个灰度级,但要求中灰度差不小于人眼视觉阈值的灰度级必须映射到中不同的灰度级.由于确保了映射到同一个灰度级的多个灰度级之间差值小于阈值,所以并没有减少人眼能正确感知的相邻像素对的数量.因此,在全局不倒序约束下,把图像中的灰度级序列映射到能得到最优图像:
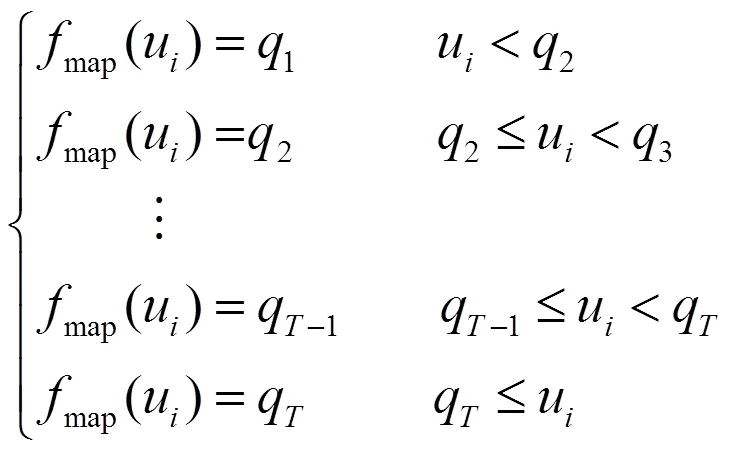
令为中灰度级数量,而为中灰度级数量.当时,有map不倒序地把中每个灰度级分别映射到中不同灰度级,使人眼完全感知到图像中所有相邻像素对的灰度差.当时,必然有不同灰度级映射到同一个灰度级,也就是在映射的过程中发生灰度级合并了,灰度级合并可能导致存在灰度差异的相邻像素对变成灰度相同,使这部分相邻像素对包含的图像信息人眼不可见.设计快速算法满足灰度级合并使图像中灰度差消失的相邻像素对最少,是解决本最优化问题的核心.
2 图像最优化快速算法
本文把灰度值分别与灰度级v、v相等的像素对的数量称为灰度级v、v合并的代价.由于式(3)的约束,灰度级合并必然是中相邻灰度级合并在一起,所以很容易想到的合并策略是迭代地进行代价最小相邻灰度级合并,然而这样不一定能得到最优合并决策.以图1(a)为例,假定一幅图像只有6个灰度级,这6个灰度级按从小到大排序分别是:A、B、C、D、E、F.图中标示出了所有灰度级间合并代价.现需要把灰度级数量从6个合并到4个.灰度级C、D间合并代价为1最小,先合并C、D得到新灰度级CD,如图1(b1)所示;更新代价后得到图1(b2),此时B与CD合并代价为9最小,B与CD合并成BCD,如图1(b3)所示.然而把B、C合并成一个灰度级,D、E合并成一个灰度级,如图1(c1)所示,更新代价后如图1(c2),显然图1(c2)合并的代价要小于图1(b3).由此可见,迭代单步最优合并不一定是全局合并最优.

(a)原始灰度级序列;(b1)、(b2)、(b3)为迭代合并最小代价相邻灰度级;(c1)、(c2)为代价最小合并决策
下面仍以图1为例说明本文将要使用的图像优化方法的快速算法.图1(a)有6个灰度级,需要把灰度级压缩成4个,现寻找代价最小合并决策.对灰度级按小到大排序,给每个灰度级一个编号,如表1所示.

表1 灰度级编号表
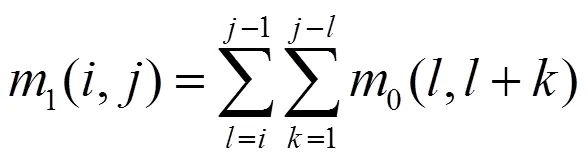
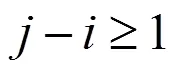
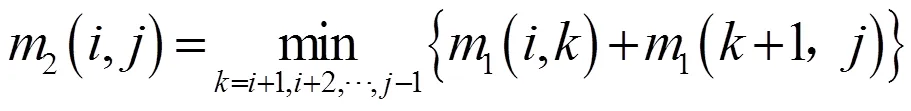


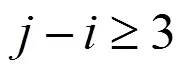

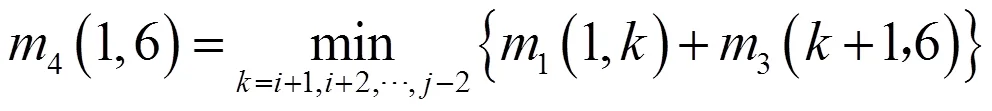
同样3(+1,6)也可由2最后一列与1计算得到,而2可由1计算出来.从而2、3在最优化过程中只须计算最后一列元素,4只有最右上角元素需要计算.构造矩阵、矩阵.其中:

矩阵用于记录式(6)、(7)、(8)中满足合并代价最小的,从而本最优化方法只需要计算1、、3个矩阵.
本文所提最优化快速算法有如下5个步骤:
1)统计图像直方图,得到图像中像素数量非0的灰度级以及此类灰度级的数量,并对灰度级按小到大进行编号,如表1所示.如果不大于,转第5步;如果大于,转第2步;
3)计算灰度级合并成一个灰度级的代价1矩阵;
4)由1计算矩阵;
5)得到最优图像.
2.1 计算代价M1矩阵
1矩阵所有元素都初始为0,遍历图像所有相邻像素对.对于任意像素对,假如其两个像素灰度值对应的灰度级序号为()其中,则1元素1()=1()+1.从而可以得到任意两个灰度级对应的代价,也就是0矩阵.对1从左到右按式(11)累加可以得到式(12).

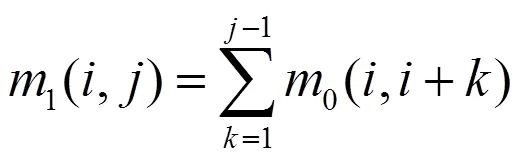
然后按式(13)从下到上累加可以得到式(5).
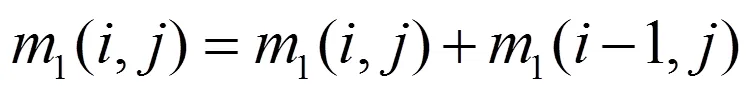
2.2 计算P、E矩阵
矩阵下所有元素都为初始值为0,第一列元素为1中最后一列元素,其它元素由下式计算:

2.3 得到最优图像


3 实验结果与分析

在所有满足全局不倒序的图像优化方法中,最常见的是直方图均衡,另外分组直方图均衡(GLG)和OCTM算法是两个引起较多关注的方法.这3种算法的对比度增强性能在图2与表2中与本文方法进行比较.需要指出的是OCTM方法最大化一种图像全局对比度的评价指标,而直方图均衡是某种意义上最大所谓的图像信息熵.
本文挑选了2幅灰度级多的图像,图像灰度级越多包含的探测识别信息可能也越多,优化空间更大,由此充分体现本全局图像优化方法的优异性能.图2中第一行图像是室内场景,而第二行图像是户外,相较于其它方法,本文方法所得图像中有最多景物能被人眼看见.如表2所示,本文方法有最多相邻像素灰度差人眼可见,而OCTM最少.因此在全局不倒序约束下,本文方法能使图像中最多相邻像素间灰度差被人眼感知到,从而某种意义上使图像中最多景物信息被人眼感知到.
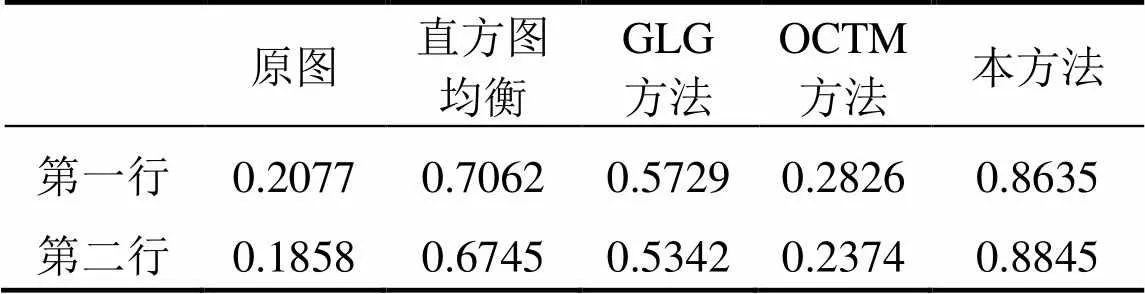
表2 人眼能正确感知的景物信息评分

图2 图像优化方法性能对比
[1] Wu X. A Linear Programming Approach for Optimal Contrast-Tone Mapping[J]., 2011,20(5):1262-72.
[2] Yu L, Su H and Jung C. Perceptually Optimized Enhancement of Contrast and Color in Images[J]., 2018(6):36132-36142.
[3] Jung C, Sun T. Optimized Perceptual Tone Mapping for Contrast Enhancement of Images[J]., 2017,27(6):1161-1170.
[4] 范晓鹏,蔡铁峰,朱枫.实现人眼灰度感知信息最大化的图像增强算法[J].计算机辅助设计与图形学学报,2015,27(10):1900-1906.
[5] Niu Y, Wu X and Shi G, Image Enhancement by Entropy Maximization and Quantization Resolution Upconversion [J].,2016,25(10):4815-4828.
[6] Wan M, Gu G, Qian W, et al. Particle swarm optimization-based local entropy weighted histogram equalization for infrared image enhancement[J]., 2018,91:164-181.
[7] Kansal S, Purwar S and Tripathi R. Enhancement of Image using Maximum Entropy Bi-Histogram Equalization[C]/2018 3rd International Conference on Communication and Electronics Systems (ICCES), 2018:728-732.
[8] Kanmani M, Narsimhan V. An image contrast enhance- ment algorithm for grayscale images using particle swarm optimization[J]., 2018,77(18):23371-23387.
[9] Agrawal S, Panda R, Mishro P K, et al. A novel joint histogram equalization based image contrast enhance- ment[J]., 2019.DOI: 10.1016/j.jksuci.2019. 05.010.
[10] Jayant N. Signal compression: technology targets and research directions[J]., 1992,10(5):796-818.
[11] Chou C, Li Y. A perceptually tuned subband image coder based on the measure of just-noticeable-distortion profile[J]., 1995,5(6):467-476.
Global Image Optimization with Gray Difference Perceptible by the Most Neighboring Pixels
CAI Tiefeng
()
Image contrast optimization can make more detection and recognition information in the image perceived by human eyes. The existing image optimization methods lack reasonable quantitative indicators, and the optimized image does not achieve the optimal detection and recognition for human eyes. Even after optimization, the information of the scene that can be detected and recognized by human eyes could be reduced. In this paper, based on the recognition that the contour and texture information of the scene in the image is mainly reflected in the gray difference of neighboring pixels, the paper designs a fast algorithm for global image optimization with the gray difference perceptible by the most neighboring pixel pairs as the quantitative index. Experimental results show that compared with the existing global image optimization methods, the image optimized by the proposed method has the most neighboring pixel pairs perceptible, which makes the image detection and recognition for human eyes optimal in a sense.
detection and recognition; image optimization; contrast enhancement
2019-11-27
深圳职业技术学院校级青年重点资助项目(6018-22k370199991)
蔡铁峰,男,湖南益阳人,助理研究员,工学博士,研究方向:图像优化、VR/AR/MR.
TP391.41
A
1672-0318(2020)03-0003-05
10.13899/j.cnki.szptxb.2020.03.001
