基于全局和局部多特征的图像增强算法

刘玉洁，朱韶平

(珠海城市职业技术学院， 广东 珠海 519090)

1 引 言

图像增强是计算机视觉的重要研究领域。在实际图像展示或者获取时，数字图像常常会遇到质量较低、重要图像信息不够明显等情况[1]，因此在实践中常用图像对比度增强来调整质量以获得更好的人类视觉感知力[2]，图像增强成为图像处理、视频处理、人脸识别中非常重要的预处理步骤。当前基于空间域技术的图像增强算法可以分为全局方法和局部方法。全局增强方法基于整个图像的信息(亮度和饱和度)来增强图像，其中一个典型的算法就是直方图均衡化。直方图均衡化及其优化方案由于其简单性和有效性，成为图像对比度增强的最常用算法之一。Kim[3]提出了一种双直方图均衡(BBHE)来保持平均亮度，该算法基于平均亮度，将原始直方图分为两个子直方图，每个子直方图都进行增强处理再进行融合。苑豪杰等[4]提出了一种多子图像直方图均衡算法，在使用中间亮度将原始直方图分为两个子直方图的基础上进一步进行分解，最后将原始直方图分解为多个直方图，通过重映射和均衡化处理更好地保持了图像增强后的细节。Menotti等[5]提出了两种新颖的多重直方图(Multi-HE)技术，将输入图像分解成几个子图像，并对每个图像应用经典的直方图均衡处理。与传统的直方图均衡化方法相比，他们的方法可以保留更多的亮度并产生更自然的图像。但是上述方法需要预先设置成本函数的加权常数，自适应能力较弱。局部增强方法根据信息(亮度、饱和度和Retinex)及其邻居的信息来增强每个像素的图像。越琳等[6]提出了一种针对直方图的均衡化增强技术，消除了均衡化图像增强中遇到的平均亮度偏移以及高频区可能发生的对比度过强带来的质量问题并提升了鲁棒性。 Meylan等[7]使用基于Retinex的自适应滤波器来增强自然彩色图像，在晕圈区域的彩色图像获得了很好的增强效果，但是其方法需要选择适当的滤波器大小以减少光晕图像并为极高的动态范围图像引入全局色调映射。杜雯超[8]使用脉冲耦合神经网络算法搜索与优化自适应遗传算法相结合,实现了PCNN图像处理时参数的自动设定,解决了传统PCNN在图像增强时参数设定困难的问题。Jobson等[9]提出了一种带有颜色恢复(MSRCR)的多尺度Retinex来恢复颜色，通过取像素与相邻像素的加权平均值之比来计算像素的颜色值，但是这种方法的一大缺点是会产生异常的色移和光晕效果[10]。李垚峰等[11]提出了一种基于Retinex的伽马校正，以减少光晕效应，但是此方法不能自动确定伽玛值，因此自适应性较差。刘冬梅等[12]提出了结合Retinex校正和显著性的主动轮廓图像分割算法。王浩等[13]基于人眼的遮盖效应提出基于高斯核平滑滤波的Retinex图像增强算法，利用像素细节信息的丰富程度实现了照度估计，有效提高了红外图像的对比度。

上述算法都立足于单一使用局部信息或全局信息，而对于两者之间的相互联系则考虑不足，因此本文提出了一种基于全局和局部信息的图像增强算法，更全面地利用图像信息获得更好的增强效果。

2 增强算法框架

2.1 局部信息增强

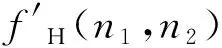
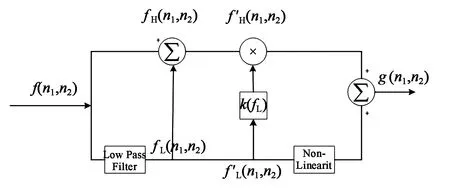
图1 局部信息增强算法框架Fig.1 Local information enhancement algorithm framework

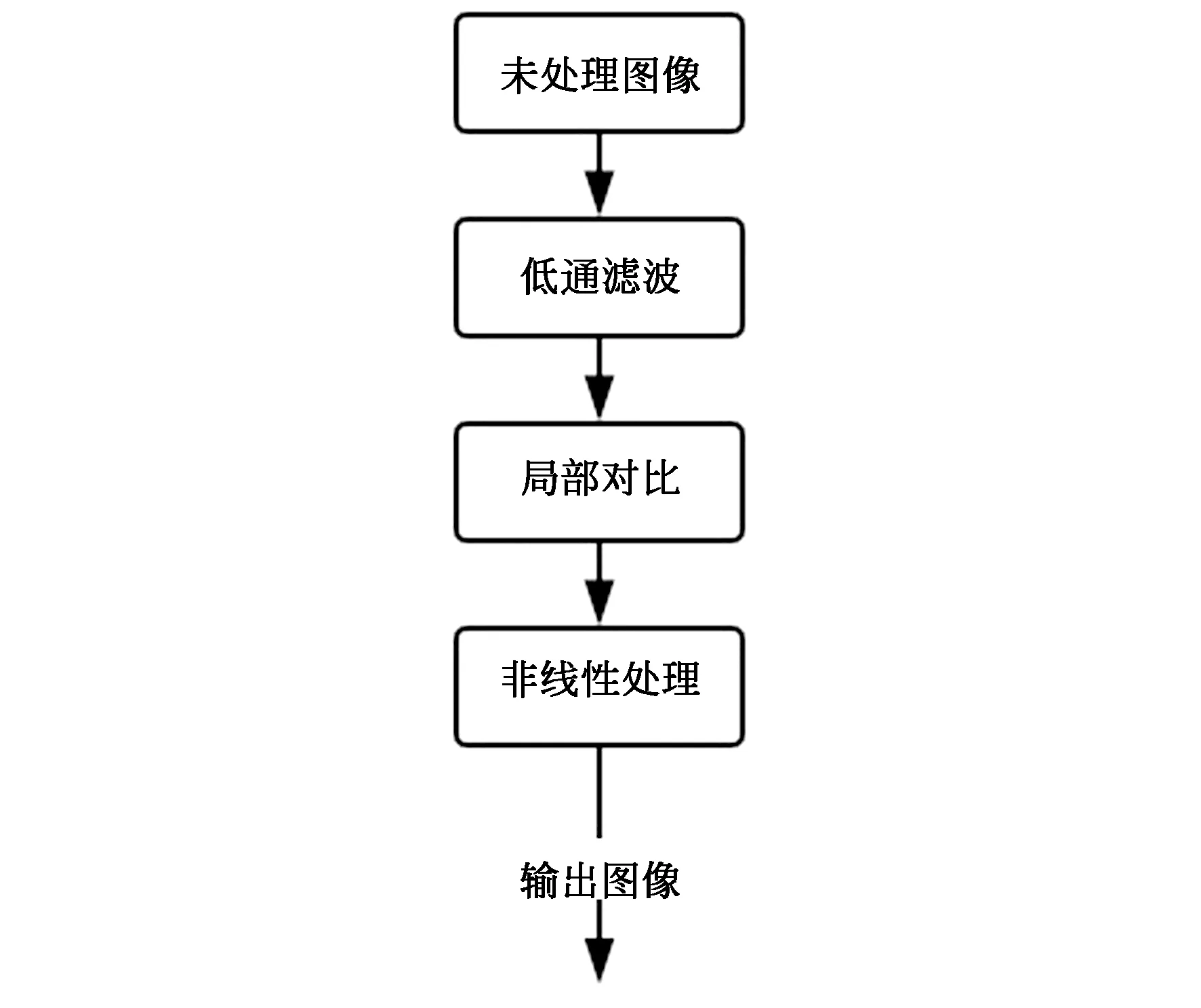
图2 局部图像修改流程Fig. 2 Local image modification process

该算法在根据局部亮度平均值修改局部对比度的基础上修改局部亮度平均值。对于典型的图像，出于视觉目的，通常期望增加重要区域的局部对比度，因此本文将k(fL)选为大于1的常数， 使用的低通滤波操作由公式(1)完成:

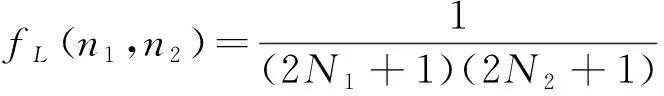
(1)

2.2 融合全局信息的增强

传统的局部对比度增强算法无法利用目标区域以外的的图像像素信息,因此对目标区域的噪声敏感。对于图像全局信息而言，为了增强局部细节往往会带来噪声的增加。为了避免这种情况，一些变换域的图像增强算法利用多尺度分析将图像分解到不同子带,将子带中的全局图像信息进行调整来优化图像增强的性能。这类算法的优势是可以同时考虑图像的全局信息和局部信息,但是由于全局信息的数据量大会导致计算复杂度的提升。本文提出的算法利用邻域伽马校正算法实现局部对比度增强,同时利用局部对比度与全局对比度的比例作为权重系数的判定依据，伽马校正的计算公式为

(2)

式中：I(x,y)为输入图像的灰度值;O(x,y)为伽马校正后的灰度值;γ为校正系数。在传统伽马校正算法中,每个图像对应一个固定的γ值,主要依赖专家打分法进行设置因此缺乏自适应能力，本文为了提升算法的自适应能力，结合邻域信息的伽马校正算法对图像全局所有像素的邻域信息都利用伽马校正系数γ(x,y)进行计算，公式为

(3)

从公式(3)可以看到,像素对应的伽马系数γ(x,y)将图像的局部信息和全局信息都考虑进去， 通过其相互关系自适应调整γ值。其中α也可以由人工设置，在α的幂系数保持不变时,α越小则γ越小,因此对黑暗区域的增强效果更佳，α为1则不对图像做增强处理。

3 实 验

本文将所提方法的增强结果与主流图像增强方法(SVLM[14]、MSRCR[15]、Contourlet[16]、SWT[17])的效果进行了比较。图3显示了用本文算法获得的照明图像的增强结果，左边是原始图像，右边是增强后的图像。

图3 图像增强效果图Fig.3 Image enhancement effect

表1为对比算法和本文算法在图像增强的指标对比。可以看出, 在均采用自适应阈值处理方法时，平稳小波变换(SWT)的增强效果要比小波变换的增强效果好，但实际处理过程中两者在图像边缘处都出现了伪 Gibbs 失真。而本文的增强效果要比SWT的增强效果好，实验结果中基本看不到伪Gibbs 失真。另外采用本文的自适应阈值处理方法所得到的结果图像的均方根误差(RMSE)值最高, 清晰度也最大，因此所得图像的细节最丰富。

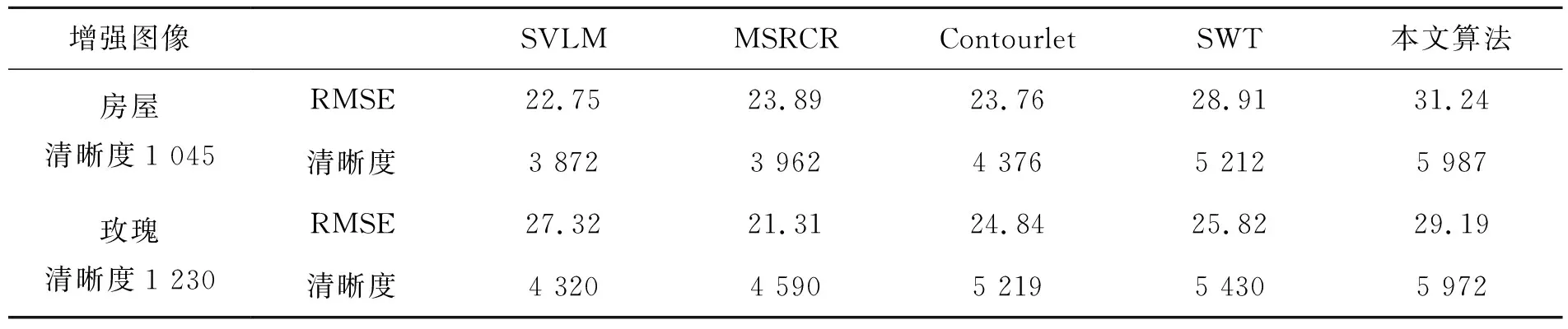
表1 图像增强数据指标对比Tab.1 Image enhancement data index comparison

4 结 论

本文提出了一种基于局部和全局信息的图像增强算法，该算法将图像分为低通滤波和高通滤波两部分，低通滤波分量控制高通滤波分量的幅度以增加局部对比度。然后对低通分量以非线性的方式修改图像的局部亮度平均值，并将其与处理后的高通分量进行融合。在与其他算法的对比实验中可以看出，本文提出的算法在运算速度、稳定性、增强效果等方面都具有更好的表现，能满足图像增强算法高效的要求，有效改善图像质量，丰富图像信息。