基于LBP与LSSVM的数字图像分类算法

张艮山，田建恩，张 哲

(石家庄学院 教育技术中心，河北 石家庄 050035)

1 引 言

随着互联网的发展，互联网中的图像内容信息越来越丰富，种类越来越多，如何实现数字图像的精确分类在机器视觉领域引起了广泛关注[1-4]。

图像分类技术的发展经历了多个阶段，从最开始的手写体阿拉伯数字识别[5]到后来的包含过万类图像数据集的分类[6-7]，伴随着数据集规模增长的是图像分类模型性能的逐步提升。整体来说，对于单标签图像分类问题，可以被分为以下3大类别：跨物种语义级别图像分类[8]；子类细粒度图像分类[9]；实例级别图像分类[10]。跨物种的语义级别图像分类，其主要目的是在不同物种层面进行识别，识别得到的结果为不同的类别，例如动物、植物类别。相对于跨物种的图像分类，子类细粒度图像分类级别更低一些。它往往是同一个大类图像中的子类图像的分类，如不同飞机类的分类、不同猪类的分类、不同果实的分类等。如果要区分不同的个体而不仅仅是物种类或者子类，则是实例级别的图像分类，最典型的任务就是人脸识别。

就应用层面而言，跨物种的语义级别分类任务在实际中最常见。为了在一些算力有限的小型嵌入式设备(如手机、平板电脑)中实现中小规模数字图像数据集的分类问题，考虑到局部二值模式(LBP)算法具有的运算速度快、对图片光照不敏感、可以充分提取图片的纹理信息等特点，同时考虑到最小二乘支持向量机(LSSVM)算法将支持向量机(SVM)优化问题的非等式约束用等式约束替换，极大地减小了计算量，使得LSSVM算法具有极好的对小型嵌入式设备的适应性，本文针对性地提出了一种基于LBP和LSSVM的数字图像分类方案，该方案包含两个模块：基于LBP特征提取的特征数据集构建模块；基于LSSVM的最优图像分类器构建模块。本文所提出的算法与传统的基于SVM的图像分类算法[11]、基于极限学习机的图像分类算法[12]和基于Hopfield神经网络的图像分类算法[13]进行了比较，在宏查准率、宏查全率和分类时间这几个典型性能指标的测试上，本文所提出的LBP-LSSVM算法均表现出了优异的性能。

2 理论基础

2.1 LBP算法

在LBP[14]算法中，原始图像按照一个区块大小为3行×3列的原则被划分为多个区块，中心像素点的像素灰度值与相邻像素点的像素灰度值进行比较，比较阈值被设置为区块的中心像素值。若相邻像素值大于中心像素值，则对应的相邻像素点被标记为1，否则为0。这样，一个区块中边沿部分的8个像素点在完成一次比较之后可产生8位二进制数，按照顺时针旋转的规则将该二进制数转换为十进制数，就可以得到一个唯一的LBP码，LBP码共计256种。LBP码被用于反映该3×3区域的纹理信息，如图1所示，这一过程用数学公式可以表示为:

(1)

其中:pxi和pxc分别为相邻像素点的值和中心像素点的值，(xc,yc)表示中心像素点的坐标。

为了适应不同尺度的纹理特征，同时实现旋转不变性，文献[15]设置了一种改进型的LBP 算子，用圆形的区块代替了正方形区块，改进型LBP 算子在半径为R的圆形区块内允许有P个(P为任意数)像素点，其坐标由公式(2)确定：

(2)

通过式(2)可以计算任意多个采样点的坐标。一个包含P个边沿像素点的LBP算子可以产生2P种二进制模式，当一个区块内的边沿像素点数增加时，对应的二进制模式的类别数是呈指数级别递增的。这种情况将给图像特征的提取、识别、分类及存取带来极大挑战。

为了解决二进制模式即LBP码数量过多的问题，文献[15]提出了一种“均匀模式”(Uniform Pattern)来降低LBP码的种类数量。文献[15]中提出，在现实世界采集到的图像中，绝大多数LBP码最多只包含两次从1到0或从0到1的变化。因此，“均匀模式”被定义为：当某个LBP码所对应的P位二进制数从0到1或从1到0的变化最多只有两次时，该LBP码就称为一个均匀模式类。除均匀模式类以外的模式都归为另一类，称为混合模式类。通过这样的改进，LBP码的种类大幅减少，数量由原来的2P种减少为P(P-1)+1种，其中P表示区块内的采样点数即边沿像素点数。

图像分类算法的LBP特征向量构建的一般步骤为：首先确定区块大小，然后通过LBP算法使用大小为M×N的原始图像生成大小为(M-2)×(N-2)的LBP图，再根据LBP图中像素值统计其LBP直方图，以直方图构成特征向量。

图1 LBP码生成过程Fig.1 Generation process of LBP code

2.2 LSSVM算法

支持向量机(Support Vector Machine, SVM)算法建立在统计学习理论的VC维理论和结构风险最小原理基础上[16]。该算法在解决中小样本数据集的识别中表现出许多特有的优势。SVM的主要思想是建立一个超平面作为样本点的分隔面, 使得正例样本和反例样本之间的隔离边缘距离被最大化。

设有样本集D={(xi,yi),xi∈Rd,yi∈{-1,1},i=1,2,…,N}，xi为d维特征向量，yi为标签。SVM的分隔面方程为：

ωx+b=0，

(3)

其中ω为权重向量，b为分类阈值。SVM问题可以归结为如公式(4)所示的不等式约束。

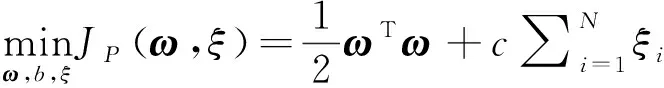
(4)

LSSVM和SVM的区别在于，LSSVM将SVM中的不等式约束优化为等式约束，从而大大方便了拉格朗日乘子的求解，QP问题被LSSVM转化为解线性方程组的问题[17]。

LSSVM问题等价于如公式(5)所示的约束。

(5)

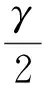
(6)

分别对ω,b,e,αi求偏导并令其为0，得到公式(7):

(7)

整理可得：

(8)

其中Y=(y1,…,yN)T;Ωij=K(xi,xj);I为单位矩阵；I1为只包含元素1的矩阵。

求解后得到：

(9)

其中K(·,·)为核函数。考虑到RBF核函数的参数较少且非线性映射能力极强，本文所设计的LSSVM分类器的核函数采用了径向基核函数，其形式如公式(10)所示。

(10)

3 算法方案设计

本文所设计的基于LBP直方图特征与LSSVM算法的数字图像分类算法主要包含特征数据集构建模块和最优分类器构建模块两部分，其详细运行步骤如下：

(1)将图像数据集进行分层抽样，将70%的图像样本划分为训练数据集，剩余30%的图像样本划分为测试数据集；

(2)假设图像样本的尺寸均为M×N，设定邻域大小为3×3，对训练数据集中图像样本进行LBP图构建，然后按照公式(11)对每张LBP图进行LBP直方图特征向量构建，所有的特征向量添加标签，然后构成新的LBP直方图特征训练数据集；

(11)

(3)设定LSSVM算法的优化参数γ及核函数参数σ的寻优范围为[-20,20]并在该范围内使用训练数据集进行参数寻优，构建最优分类模型；

原题：Models of the Earth's crust from controlled－source seismology—where we stand and where we go？

(4)按照步骤(2)中方法，对部分原始图像构成的测试数据集进行LBP直方图特征测试数据集构建，然后对送入步骤(3)中得到的最优分类模型进行分类并计算各项性能指标。

4 公开数据集的分类测试

为验证本文所提出算法的有效性，两个公开的图像分类数据集被用于分类测试。两个数据集分别为人脸数据集YALE和Kaggle的Flowers Recognition数据集。人脸数据集YALE共包含165 幅灰度图像，分别属于15个人，每个人对应有11 幅不同的脸部图像，这11幅图像分别为：中心光、戴眼镜、快乐、左侧光、不戴眼镜、正常表情、右侧光、悲伤、困倦、吃惊和眨眼。部分样本图像如图2所示。Kaggle的Flowers Recognition数据集共包含4 326张图像，分别属于5种花：雏菊，向日葵，玫瑰，蒲公英和郁金香。

图2 人脸数据集YALE中部分样本图片Fig.2 Partial sample images of face dataset YALE

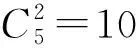
使用同一个由LBP特征向量构建的训练数据集，以本文所提出算法(核函数使用径向基核函

通过表2可以发现，本文所提出的算法整体上具有最佳的性能表现，主要是因为本文所提出算法选取的LBP直方图特征能够充分反映数字图像的内在规律，同时LSSVM保持了SVM的结构风险最小化特征，因此泛化能力极强。LSSVM的速度达到了与极限学习机算法同等水平的速度，这主要是因为，虽然在LSSVM算法中所有样本数据点均为“支持向量点”，计算核矩阵时运算量较大，但LSSVM 将分类问题的凸二次规划问题转化为求解线性方程的问题，大大加快了分类速度，在数据集样本量较大时，运算时间缩短将更为明显。

表1 种最优分类模型的训练误差Tab.1 Training error of four optimal classification models

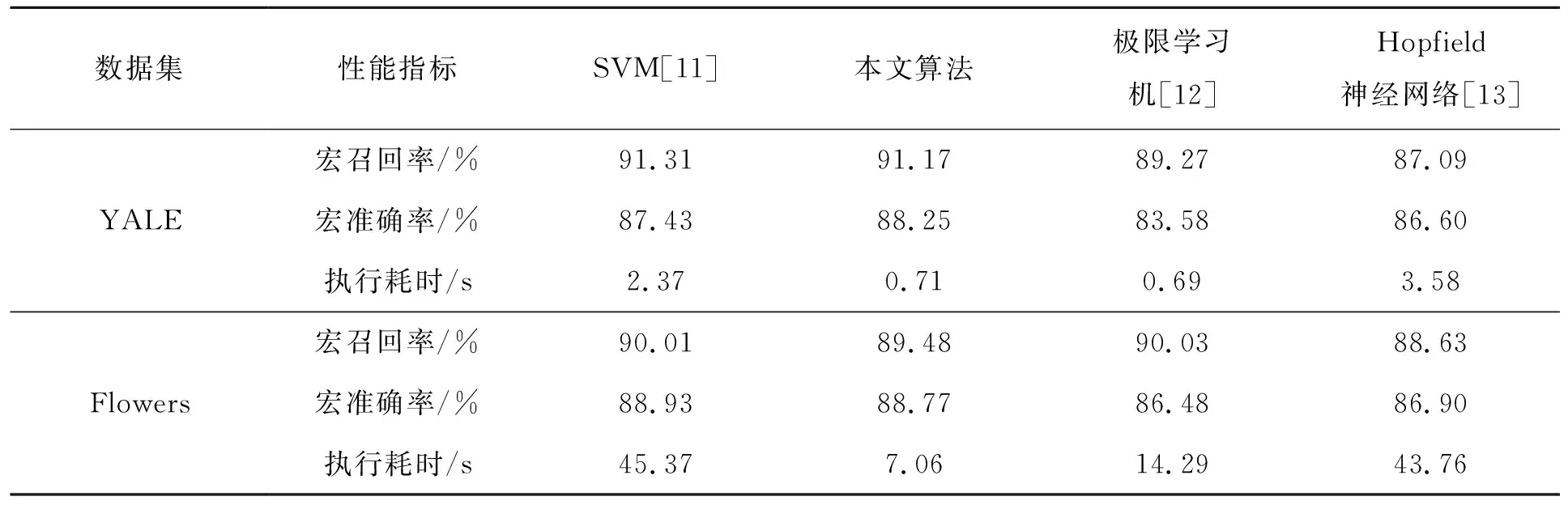
表2 测试数据集上4种算法的分类结果及执行效率比较Tab.2 Comparison of classification results and execution efficiency of four algorithms on test dataset

5 结 论

针对数字图像的高精度分类问题，本文提出了一种基于LBP直方图特征的LSSVM数字图像分类算法。在该算法中，LBP算子被用于进行数字图像的LBP图构建，LBP图的直方图被用于构建图像样本的特征向量，最后大量样本的特征向量构建的训练数据集被送入 LSSVM进行分类模型的构建。在测试数据集的分类测试中，核函数使用径向基核函数时，本文所提出算法与3种分别基于传统支持向量机算法、极限学习机算法和Hopfield神经网络方法的图像分类算法进行了比较，在宏查准率、宏查全率和分类时间这几个典型性能指标的测试方面，本文所提出的LBP-LSSVM算法均表现出了优异的性能。