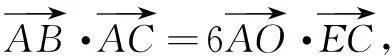三角形中的填空压轴题管窥

詹梓铭

(湖北省武汉理工大学数学系2017级，430070)

这些年江苏高考数学试卷的第12、13、14这几道填空题都比较难,一般作为第一部分填空题的压轴题来使用.命题方向主要涉及三角形与函数的性质(数形结合)、基本不等式应用、三角函数最值、数列等几个C级考点的交汇．本文主要就此类填空压卷题作简要分析,其中三角函数问题经常与最值问题密切联系,平面向量则常要利用平面基向量法求解．

一、利用换元法求最值

评注 这类题需要考生联想到sinθ+cosθ与sinθcosθ之间的内在关系，通过换元转化为有理函数的最值问题.求解时必须注意换元前后变量的取值范围．类似试题如2018年全国联赛四川预赛试题第3题、2016年全国联赛江苏预赛试题第11题等，解题的关键都是如此．

二、利用基本不等式求最值

例2 在∆ABC中,sinA=2cosBcosC,则sin2B+sin2C的最大值是______．

解 在∆ABC中， 显然sinA>0,因此cosBcosC>0.因为同一个三角形中至多有一个钝角,于是必有cosB>0,cosC>0,即B、C都是锐角.

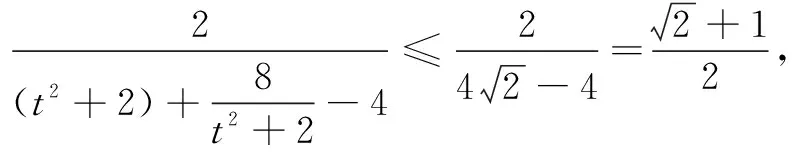
三、利用三角形特有性质求三角函数最值

分析 这道题解法很多,但最巧妙的是下面的办法:显然A、B、C都不是直角,由于一个三角形中钝角至多一个,若A是钝角，则条件等式左边为负,右边为正,矛盾.所以角A是锐角．

四、利用基向量法求解向量背景下的三角形问题